TRƯỜNG ĐẠI HỌC SƯ PHẠM HÀ NỘI
Thi vào lớp 10 chuyên Toán-Tin
Năm học 2008-2009. Thời gian làm bài: 150 phút
Câu 1: Ba số dương $a,b,c$ thỏa mãn $\sqrt{a}+\sqrt{b}\ne \sqrt{c}$ và $a+b=(\sqrt{a}+\sqrt{b}-\sqrt{c})^2$. Chứng minh đẳng thức:
$$\displaystyle{\frac{a+(\sqrt{a}-\sqrt{c})^2}{b+(\sqrt{b}-\sqrt{c})^2}=\frac{\sqrt{a}-\sqrt{c}}{\sqrt{b}-\sqrt{c}}}$$
Câu 2.
1. Với mỗi số dương $a$ thỏa mãn $a^3=6(a+1)$, chứng minh phương trình sau vô nghiệm:
$$x^2+ax+a^2-6=0$$
2. Tìm tất cả các giá trị của $a,b$ sao cho
$$2(a^2+1)(b^2+1)=(a+1)(b+1)(ab+1)$$
Câu 3:Ba số dương $a,b,c$ đôi một khác nhau và thỏa mãn đồng thời các điều kiện sau:
$(i): a$ là ước của $b+c+bc$
$(ii): b$ là ước của $a+c+ac$
$(iii): c$ là ước của $a+b+ab$
CMR: $a,b,c$ không đồng thời là các số nguyên tố
Câu 4: Cho tam giác $ABC$. Một đường tròn $©$ đi qua các điểm $A,B$ và cắt các cạnh $CA,CB$ tại các điểm $L,N$ tương ứng $(L\ne A,C;N\ne B,C)$. Gọi $M$ là trung điểm của cung $LN$ của đường tròn $©$ và $M$ nằm trong tam giác $ABC$. Đường thằng $AM$ cắt cắt các đường thẳng $BL$ và $BN$ tại các điểm $D$ và $F$ tương ứng, đường thẳng $BM$ cắt các đường thẳng $AN$ và $AL$ tại các điểm $E$ và $G$ tương ứng. Gọi $P$ là giao điểm của $AN$ và $BL$.
1. Chứng minh $DE//GF$
2. Nếu tứ giác $DEFG$ là hình bình hành, hãy chứng minh:
$a) \Delta ALP\sim \Delta ANC\\ b)DF\perp EG$
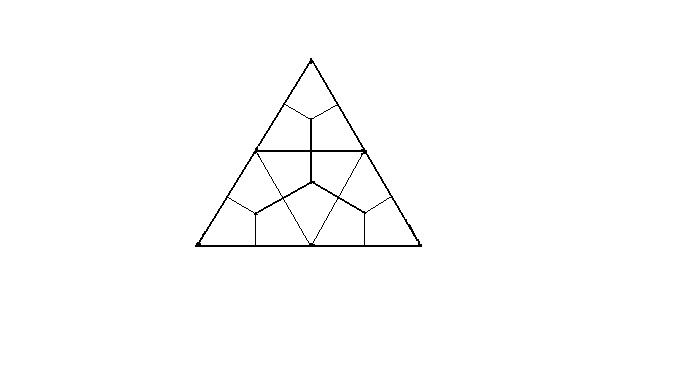
Câu 5: Cho $13$ điểm phân biệt nằm trong hay trên cạnh của một tam giác đều có cạnh bàng $6 cm$. Chứng minh rằng luôn tồm tại hai điểm trong số $13$ điểm đã cho mà khoảng cách giữa chúng không vượt quá $\sqrt{3} cm$
--------------------------HẾT--------------------------
Thấy VMF chưa có đề này nên mình đưa lên cho ae tham khảoBài viết đã được chỉnh sửa nội dung bởi minhtuyb: 21-05-2012 - 11:31