Chủ đề này có 26 trả lời

[MIM]

ĐẠI HỌC QUỐC GIA HÀ NỘI
TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN

ĐỀ TUYỂN SINH VÀO LỚP 10 HỆ THPT CHUYÊN NĂM 2012

Môn thi: Toán (Dành cho mọi thí sinh)

Thời gian làm bài: 120p (Không kể thời gian giao đề)

Câu I.

$1)$ Giải phương trình:
$\sqrt{x+9}+2012\sqrt{x+6}=2012+\sqrt{(x+9)(x+6)}$

$2)$ Giải hệ phương trình:
$\left\{\begin{matrix} x^2+y^2+2y=4 & \\ 2x+y+xy=4& \end{matrix}\right.$

Câu II.

$1)$ Tìm tất cả các cặp số nguyên $(x;y)$ thỏa mãn đẳng thức:
$(x+y+1)(xy+x+y)=5+2(x+y)$

$2)$ Giả sử $x,y$ là các số thực dương thỏa mãn điều kiện $(\sqrt{x}+1)(\sqrt{y}+1)\geq 4$. Tìm giá trị nhỏ nhất của biểu thức:

$P=\frac{x^2}{y}+\frac{y^2}{x}$

Câu III.

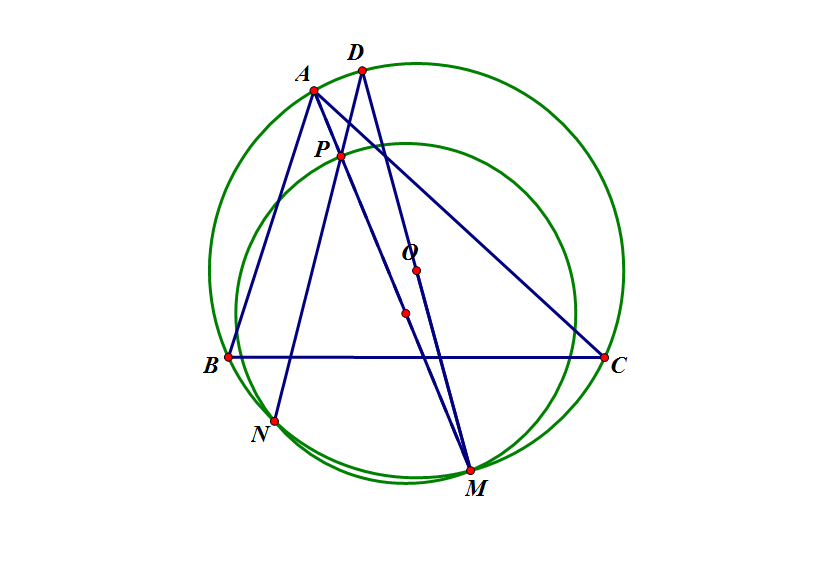
Cho tam giác nhọn $ABC$ nội tiếp đường tròn tâm $O$. Gọi $M$ là một điểm trên cung nhỏ $BC$ ($M$ khác $B,C$ và $AM$ không đi qua $O$). Giả sử $P$ là một điểm thuộc đoạn thẳng $AM$ sao cho đường tròn đường kính $MP$ cắt cung nhỏ $BC$ tại $N$ khác $M$

$1)$ Gọi $D$ là điểm đối xứng với điểm $M$ qua $O$. Chứng minh rằng $N,P,D$ thẳng hàng.

$2)$ Đường tròn đường kính $MP$ cắt $MD$ tại $Q$ khác $M$. Chứng minh rằng $P$ là tâm đường tròn nội tiếp tam giác $AQN.$

Câu IV.

Giả sử $a,b,c$ là các số thực dương thỏa mãn $a\leq b\leq 3\leq c;c\geq b+1;a+b\geq c.$ Tìm giá trị nhỏ nhất của biểu thức:
$Q=\frac{2ab+a+b+c(ab-1)}{(a+1)(b+1)(c+1)}$

..............................HẾT..............................

DOWNLOAD:

+ http://www.mediafire...bmc9jk41pfp9p51

Bài viết đã được chỉnh sửa nội dung bởi huynhmylinh: 10-06-2012 - 16:11

[hoangtrong2305]

Câu I.
$2)$ Giải hệ phương trình:
$\left\{\begin{matrix} x^2+y^2+2y=4 & \\ 2x+y+xy=4& \end{matrix}\right.$

$\left\{\begin{matrix} x^2+y^2+2y=4 & \\ 2x+y+xy=4(*)& \end{matrix}\right.$

$\Leftrightarrow \left\{\begin{matrix} x^2+y^2+2y=4 & \\ 4x+2y+2xy=8& \end{matrix}\right.$

$\Leftrightarrow x^{2}+2xy+y^{2}+4x+4y=12$

$\Leftrightarrow (x+y)^{2}+4(x+y)-12=0$

$\Leftrightarrow \begin{bmatrix} x+y=2\\ x+y=-6 \end{bmatrix}$

$\Leftrightarrow \begin{bmatrix} x=2-y\\ x=-6-y \end{bmatrix}$


TH1: $x=2-y$

Thế vào phương trình $(*)$

$2(2-y)+y+(2-y)y=4$

$\Leftrightarrow -y^{2}+y=0$

$\Leftrightarrow \begin{bmatrix} y=1\Rightarrow x=1\\ y=0\Rightarrow x=2 \end{bmatrix}$



TH2: $x=-6-y$

Thế vào phương trình $(*)$

$2(-6-y)+y+(-6-y)y=4$

$\Leftrightarrow y^{2}+7y+16=0$

$\Delta =-15<0$

$\Rightarrow$ phương trình vô nghiệm


KẾT LUẬN: Hệ phương trình có $2$ nghiệm $(x;y)$

$$\boxed{(x;y)=\begin{Bmatrix} (1;1);(2;0) \end{Bmatrix}}$$





-------------------------------------------------------------------------------
Bài này chắc khuyến mãi thôi kệ, pùn pùn làm chơi

Bài viết đã được chỉnh sửa nội dung bởi hoangtrong2305: 10-06-2012 - 09:58

[hhhntt]

Làm câu II bài 2 trước:
$(\sqrt{x}+\sqrt{y}+2)^{2}\geqslant 4(\sqrt{x}+1)(\sqrt{y}+1)\geqslant 16$
$\Rightarrow \sqrt{x}+\sqrt{y}\geq 2$
$2(x+y)\geqslant (\sqrt{x}+\sqrt{y})^{2}\geqslant 4 \Rightarrow x+y\geq 2$
Áp dụng bất đẳng thức Cauchy - Shwarz:
$P\geqslant \frac{(x+y)^{2}}{x+y}=x+y\geqslant 2$
Vậy $P_{Min}=2$ khi $x=y=1$

Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 10-06-2012 - 11:12

[L Lawliet]

Câu I.

$1)$ Giải phương trình:
$\sqrt{x+9}+2012\sqrt{x+6}=2012+\sqrt{(x+9)(x+6)}$

Bang chủ chém câu 2 em chém câu 1

$\boxed{Solution}$
ĐKXĐ: $x\geq -6$

$$PT\Leftrightarrow \sqrt{x+9}(1-\sqrt{x+6})-2012(1-\sqrt{x+6})=0$$
$$\Leftrightarrow (\sqrt{x+9}-2012)(1-\sqrt{x+6})=0$$

• $\sqrt{x+9}-2012=0\Leftrightarrow x+9=2012^2\Leftrightarrow x=4048135$ (TM)
• $1-\sqrt{x+6}=0\Leftrightarrow x+6=1\Leftrightarrow x=-5$ (TM)

Vậy nghiệm của phương trình là $\boxed{x=-5;4048135}$

$\boxed{Q.E.D}$

[Zaraki]

Câu II.

$1)$ Tìm tất cả các cặp số nguyên $(x;y)$ thỏa mãn đẳng thức:
$(x+y+1)(xy+x+y)=5+2(x+y)$

SOLUTION: Ta có $$\begin{aligned} pt & \iff (x+y+1)(xy+x+y)-2(x+y)=5 \\ & \iff (x+y)(xy+x+y)+(xy+x+y)-2(x+y) =5 \\ & \iff (x+y)(xy+x+y-2)+(xy+x+y-2)=3 \\ & \iff (x+y+1)(xy+x+y-2)=3 \end{aligned}$$

Khi đó phân tích $3=3.1=(-3).(-1)$.
Xét TH:
TH1: Nếu $x+y+1=1 \implies x+y=0$ và $xy+x+y-2=3 \implies xy+x+y=5 \implies xy=5$, vô lí do $x=-y$.

TH2: Nếu $x+y+1=3 \implies x+y=2$ và $xy+x+y-2=1 \implies xy+x+y=3 \implies xy=1$. Ta tìm được nghiệm $1,1$.

TH3: Nếu $x+y+1=-1 \implies x+y=-2$ và $xy+x+y-2=-3 \implies xy+x+y=-1 \implies xy=1$. Ta tìm được nghiệm $-1,-1$

TH4: Nếu $x+y+1=-3 \implies x+y=-4$ và $xy+x+y-2=-1 \implies xy+x+y=1 \implies xy=5$, vô nghiệm.

Kết luận. Phương trình có nghiệm $\boxed{ (x;y) \in \{ (1,1),(-1,-1) \}}$ và các hoán vị.

Bài viết đã được chỉnh sửa nội dung bởi Phạm Quang Toàn: 10-06-2012 - 14:43

[L Lawliet]

$\boxed{Solution}$

Làm 1 bài hình luôn chứ câu 2 thì đề ra em chịu
Vì $D$ là điểm đối xứng với $M$ qua $O$ nên $MD$ là đường kính của đường tròn $O$
$\Rightarrow \widehat{DNM}=90^o$ (góc nội tiếp chắn nửa đường tròn tâm $O$)
Hay $DN\perp NM$ $(1)$
Trong đường tròn đường kính $MP$ có
$\widehat{PNM}=90^o$ (góc nội tiếp chắn nửa đường tròn đường kính $MP$)
Hay $PN\perp NM$ $(2)$
Từ $(1)$ và $(2)$ suy ra ba điểm $D$, $P$ và $N$ thẳng hàng (tiên đề Ơ-clit)

$\boxed{Q.E.D}$

P/s: Còn câu 2 bài hình và bài 4 nữa thôi mọi người chém cho hết nào

[namtuoc97]

[left]
SOLUTION: Ta có $$\begin{aligned} pt & \iff (x+y+1)(xy+x+y)-2(x+y)=5 \\ & \iff (x+y)(xy+x+y)+(xy+x+y)-2(x+y) =5 \\ & \iff (x+y)(xy+x+y-2)+(xy+x+y-2)=3 \\ & \iff (x+y+1)(xy+x+y-2)=3 \end{aligned}$$

Khi đó phân tích $3=3.1=(-3).(-1)$.
Xét TH:
TH1: Nếu $x+y+1=1 \implies x+y=0$ và $xy+x+y-2=3 \implies xy+x+y=5 \implies xy=5$, vô lí do $x=-y$.

TH2: Nếu $x+y+1=3 \implies x+y=2$ và $xy+x+y-2=1 \implies xy+x+y=3 \implies xy=1$. Ta tìm được nghiệm $1,1$.

TH3: Nếu $x+y+1=-1 \implies x+y=-2$ và $xy+x+y-2=-3 \implies xy+x+y=-1 \implies xy=1$. Ta tìm được nghiệm $-1,-1$

TH4: Nếu $x+y+1=-3 \implies x+y=-4$ và $xy+x+y-2=-1 \implies xy+x+y=1 \implies xy=5$. Ta tìm được nghiệm $(-5,1)$.

Kết luận. Phương trình có nghiệm $\boxed{ (x;y) \in \{ (1,1),(-1,-1),(-5,1) \}}$ và các hoán vị.

sai rồi anh!! thừa nghiệm (-5;1)

[Trần Đức Anh @@]

Sửa lại câu hình kìa, câu b là $P$ là tâm đường tròn nội tiếp tam giác $AQN$

[phuc_90]

Câu IV.

Giả sử $a,b,c$ là các số thực dương thỏa mãn $a\leq b\leq 3\leq c;c\geq b+1;a+b\geq c.$ Tìm giá trị nhỏ nhất của biểu thức:
$Q=\frac{2ab+a+b+c(ab-1)}{(a+1)(b+1)(c+1)}$

Đề năm nay câu 4 khó nhất nhỉ @_^)

Trước hết ta đơn giản biểu thức $Q$ trước đã

$Q=\frac{2ab+a+b+c(ab-1)}{(a+1)(b+1)(c+1)}$

$=\frac{1}{1+c}+\frac{ab+abc-c-1}{(1+a)(1+b)(1+c)}$

$=\frac{1}{1+c}+\left(\frac{ab-1}{(1+a)(1+b)}+1\right)-1$

$=\frac{1}{1+c}+\frac{a}{1+a}+\frac{b}{1+b}-1$

$=\frac{1}{1+c}+\frac{b}{1+b}-\frac{1}{1+a}$

Ta xử lý giả thiết

Từ $\ \ c \geq b+1$ và $\ \ a+b \geq c$ suy ra $\ \ a+b \geq b+1$ kéo theo $\ \ b\geq a\geq 1$

* Trường hợp : $\ \ \ \ b \geq 2$

Do $\ \ a+b \geq c$ nên $\ \ Q \geq \frac{1}{1+a+b}+\frac{b}{1+b}-\frac{1}{1+a}=\frac{a}{1+a}+\frac{b}{1+b}-\frac{a+b}{1+a+b}$

Vì $\ \ b \geq 2$ ta có $\ \ \frac{b}{1+b}-\frac{a+b}{1+a+b} \geq \frac{2}{3}-\frac{a+2}{a+3}$

Suy ra $\ \ Q \geq \frac{2}{3}+\frac{a}{1+a}-\frac{a+2}{a+3}=\frac{(a-1)(a+5)}{4(a+1)(a+3)}+\frac{5}{12} \geq \frac{5}{12}$

* Trường hợp : $\ \ \ \ b \leq 2$

Do $\ \ a+b \geq c$ kéo theo $\ \ Q \geq \frac{1}{1+c}+\frac{b}{1+b}-\frac{1}{1+c-b}$

Vì $\ \ c \geq 3$ nên $\ \ \frac{1}{1+c}-\frac{1}{1+c-b} \geq \frac{1}{4}-\frac{1}{4-b}$

Suy ra $\ \ Q \geq \frac{1}{4}+\frac{b}{1+b}-\frac{1}{4-b}=\frac{5}{6} \frac{(2-b)(b-1)}{(b+1)(4-b)}+\frac{5}{12} \geq \frac{5}{12}$

Vậy GTNN của $Q=\frac{5}{12}$ .Đẳng thức xảy ra khi và chỉ khi $a=1 , b=2 , c=3$

[Trần Đức Anh @@]

Bài hình:
1.Dễ dàng
2.Ta có $P,Q,M,N$ đồng viên nên $DP.DN=DQ.DM$ suy ra : $DP.PN+DP^2=DQ.QM+DQ^2$ mà $AP.PM=DP.PN$ suy ra: $AP.PM=DQ.QM+DP^2-DQ^2=DQ.QM+MP^2-MQ^2$ suy ra $MA.MP=MD.MQ$ suy ra tứ giác $A,P,Q,D$ đồng viên suy ra: $\widehat{AMN}=\widehat{PMN}=\widehat{PQN}=\widehat{ADN}=\widehat{ADP}=\widehat{AQP}$ suy ra QP là phân giác góc $\widehat{AQN}$. $(1)$
Cũng từ A,P,Q,D đồng viên suy ra $\widehat{NAM}=\widehat{NDM}=\widehat{PDQ}=\widehat{PAQ}$ suy ra AP là phân giác góc $\widehat{NAQ}$ $(2)$
Từ $(1)$ và $(2)$ ta có đpcm.

Bài viết đã được chỉnh sửa nội dung bởi Trần Đức Anh @@: 10-06-2012 - 16:26

[Zaraki]

Xin gửi mọi người link một số cách giải của bài 2 câu II đề này.

File gửi kèm

•  nhieu cach giai cho bai 2 KHTN.doc   108K   403 Số lần tải

[nthoangcute]

Câu IV.
Giả sử $a,b,c$ là các số thực dương thỏa mãn $a\leq b\leq 3\leq c;c\geq b+1;a+b\geq c.$ Tìm giá trị nhỏ nhất của biểu thức:
$Q=\frac{2ab+a+b+c(ab-1)}{(a+1)(b+1)(c+1)}$

Mình làm như thế này liệu có đúng không (Đi thi làm như thế)
Ta có: $a+b \geq c \geq b+1 \to a \geq 1 \to c \geq b \geq a \geq 1$
$$\to (a-1)(b-1)(c-1) \geq 0$$
$$\to abc-ab-bc-ca+a+b+c-1 \geq 0$$
$$\to (a+1)(b+1)(c+1) \leq 2(abc+a+b+c)$$
Lại có:
$$Q=\frac{2ab+a+b+c(ab-1)}{(a+1)(b+1)(c+1)}$$
$$\geq \frac{2ab+abc}{
(a+1)(b+1)(c+1)}$$
$$\geq
\frac{2ab+abc}{2(abc+a+b+c)}$$
Ta thấy:
$$\frac{2ab+abc}{2(abc+a+b+c)} \geq \frac{5}{12}$$
$$\Leftrightarrow 6(2ab+abc) \geq 5(abc+a+b+c)$$
$$\Leftrightarrow abc+12ab-5(a+b+c) \geq 0$$
Vì
$$ abc+12ab-5(a+b+c) \geq 3ab+12ab-5(a+b+c)$$
$$\geq 15ab-10(a+b)$$
Vì $(a-1)(b-1) \geq 0 \to ab+1 \geq a+b$
Suy ra
$$15ab-10(a+b) \geq 15(a+b-1)-10(a+b)=5(a+b)-15 \geq 5c-15 \geq 5.3-15=0$$
Suy ra BĐT luôn đúng hay ta có đpcm

Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 11-06-2012 - 12:26

[nthoangcute]

Mình nghĩ bạn ngược dấu rồi

Thanks, đã fix lại, hi hi !!!

[yeutoan11]

Có ai có đề Toán Chuyên không
Trong box tài liệu đề thi có rồi nhé.

Bài viết đã được chỉnh sửa nội dung bởi Ispectorgadget: 12-06-2012 - 17:42

[rubimeocon]

Làm câu II bài 2 trước:
$(\sqrt{x}+\sqrt{y}+2)^{2}\geqslant 4(\sqrt{x}+1)(\sqrt{y}+1)\geqslant 16$
$\Rightarrow \sqrt{x}+\sqrt{y}\geq 2$
$2(x+y)\geqslant (\sqrt{x}+\sqrt{y})^{2}\geqslant 4 \Rightarrow x+y\geq 2$
Áp dụng bất đẳng thức Cauchy - Shwarz:
$P\geqslant \frac{(x+y)^{2}}{x+y}=x+y\geqslant 2$
Vậy $P_{Min}=2$ khi $x=y=1$

Bài này mình làm theo cách sau có được k0 bạn:
Áp dụng bdt Cô-si ta có:
$ P=\frac{x^2}{y}+\frac{y^2}{x} \ge 2\sqrt{xy} $

$(\sqrt{x}+1)(\sqrt{y}+1)\ge4$ $\leftrightarrow$ $\sqrt{xy}\ge3-(\sqrt{x}+\sqrt{y})$

Dấu "=" xảy ra
$\leftrightarrow$ $\left\{\begin{array}\\\frac{x^2}{y} = \frac{y^2}{x}\\\sqrt{xy}=3-(\sqrt{x}+\sqrt{y})\end{array}\right.$
$\leftrightarrow$ $x=y=1$

$\rightarrow$ $P\ge2\sqrt{xy}=2$

Vậy $minP=2$ $\leftrightarrow$ $x=y=1$

Bài viết đã được chỉnh sửa nội dung bởi rubimeocon: 13-06-2012 - 21:03

[loc1997]

Bài này mình làm theo cách sau có được k0 bạn:
Áp dụng bdt Cô-si ta có:
$ P=\frac{x^2}{y}+\frac{y^2}{x} \ge 2\sqrt{xy} $

$(\sqrt{x}+1)(\sqrt{y}+1)\ge4$ $\leftrightarrow$ $\sqrt{xy}\ge3-(\sqrt{x}+\sqrt{y})$

Dấu "=" xảy ra
$\leftrightarrow$ $\left\{\begin{array}\\\frac{x^2}{y} = \frac{y^2}{x}\\\sqrt{xy}=3-(\sqrt{x}+\sqrt{y})\end{array}\right.$
$\leftrightarrow$ $x=y=1$

$\rightarrow$ $P\ge2\sqrt{xy}=2$

Vậy $minP=2$ $\leftrightarrow$ $x=y=1$

mjnh cug lam gan gjong ban.
moi nguoi xem thu cach lam sau cua mjnh co dug k nke:
$\frac{x^{2}}{y}+\frac{y^{2}}{x}\geq 2\sqrt{xy}$
$\frac{x^{2}}{y}+\frac{y}{x}\geq 2\sqrt{x}$
$\frac{y^{2}}{x}+\frac{x}{y}\geq 2\sqrt{y}$
tu 2 djeu tren
$\Rightarrow 2P-\frac{x}{y}-\frac{y}{x}\geq 2\sqrt{xy}+2\sqrt{x}+2\sqrt{y}=2(\sqrt{xy}+\sqrt{x}+\sqrt{y}$
ma $(\sqrt{x}+1)(\sqrt{y}+1)\geq 4 \Rightarrow (\sqrt{xy}+\sqrt{x}+\sqrt{y}\geq 3 \Rightarrow 2(\sqrt{xy}+\sqrt{x}+\sqrt{y}\geq 6$
$\Rightarrow 2P-\frac{x}{y}-\frac{y}{x}\frac{x}{y}-\frac{y}{x}6\Rightarrow 2P\geq 6+\frac{x}{y}+\frac{y}{x}$
Dau = xay ra$\Leftrightarrow x=y=1$
thay vao ta co: $2P \geq 4$
Vay Pmin=2<=>x=y=1

Bài viết đã được chỉnh sửa nội dung bởi loc1997: 14-06-2012 - 21:02

[hhhntt]

Bài này mình làm theo cách sau có được k0 bạn:
Áp dụng bdt Cô-si ta có:
$ P=\frac{x^2}{y}+\frac{y^2}{x} \ge 2\sqrt{xy} $

$(\sqrt{x}+1)(\sqrt{y}+1)\ge4$ $\leftrightarrow$ $\sqrt{xy}\ge3-(\sqrt{x}+\sqrt{y})$

Dấu "=" xảy ra
$\leftrightarrow$ $\left\{\begin{array}\\\frac{x^2}{y} = \frac{y^2}{x}\\\sqrt{xy}=3-(\sqrt{x}+\sqrt{y})\end{array}\right.$
$\leftrightarrow$ $x=y=1$

$\rightarrow$ $P\ge2\sqrt{xy}=2$

Vậy $minP=2$ $\leftrightarrow$ $x=y=1$

chỗ này là sao vậy bạn tại sao $P\geqslant 2\sqrt{xy}=2$

[Crystal]

chỗ này là sao vậy bạn tại sao $P\geqslant 2\sqrt{xy}=2$

Do $x=y=1$ như đã chứng minh ở trên khi dấu "=" xảy ra đó bạn.

[hhhntt]

mjnh cug lam gan gjong ban.
moi nguoi xem thu cach lam sau cua mjnh co dug k nke:
$\frac{x^{2}}{y}+\frac{y^{2}}{x}\geq 2\sqrt{xy}$
$\frac{x^{2}}{y}+\frac{y}{x}\geq 2\sqrt{x}$
$\frac{y^{2}}{x}+\frac{x}{y}\geq 2\sqrt{y}$
tu 2 djeu tren
$\Rightarrow 2P-\frac{x}{y}-\frac{y}{x}\geq 2\sqrt{xy}+2\sqrt{x}+2\sqrt{y}=2(\sqrt{xy}+\sqrt{x}+\sqrt{y}$
ma $(\sqrt{x}+1)(\sqrt{y}+1)\geq 4 \Rightarrow (\sqrt{xy}+\sqrt{x}+\sqrt{y}\geq 3 \Rightarrow 2(\sqrt{xy}+\sqrt{x}+\sqrt{y}\geq 6$
$\Rightarrow 2P-\frac{x}{y}-\frac{y}{x}\frac{x}{y}-\frac{y}{x}6\Rightarrow 2P\geq 6+\frac{x}{y}+\frac{y}{x}$
Dau = xay ra$\Leftrightarrow x=y=1$
thay vao ta co: $2P \geq 4$
Vay Pmin=2<=>x=y=1

đáng lẽ là $2P\geqslant 6+\frac{x}{y}+\frac{y}{x}\geqslant 8$
thì $P\geqslant 4$ à bạn có vấn đề ở đây rùi đó bạn sai ngay ở đầu phải là cộng thành $2P+\frac{x}{y}+\frac{y}{x}$ là thành $2P\geqslant 6-\frac{x}{y}-\frac{y}{x}$ là ngược dấu đó bạn sai rùi

[hhhntt]

Do $x=y=1$ như đã chứng minh ở trên khi dấu "=" xảy ra đó bạn.

bạn ơi xem lại định nghĩa về GTNN GTLN đi $p\geqslant k$ với k là hằng số cơ mà nói chung làm thế sai rùi đó $2\sqrt{xy}$ không phải là hằng số

Bài viết đã được chỉnh sửa nội dung bởi hhhntt: 15-06-2012 - 11:00