Chủ đề này có 159 trả lời

[The Collection]

$\boxed{\text{Bài toán 17}}$ Cho $PQ$ là một đường kính của đường tròn $(O)$, $A,B$ là $2$ điểm bất kì thuộc $(O)$ sao cho $A,B$ nằm cùng một nửa mặt phẳng bờ $PQ$. Gọi $C$ là giao điểm của $2$ tiếp tuyến tại $A,B$ của $(O)$. Tiếp tuyến tại $Q$ của $(O)$ cắt $PA,PB,PC$ lần lượt tại $A',B',C'$. Chứng minh rằng $C'$ là trung điểm của $A'B'$.

 

Spoiler

15088

 

$\boxed{\text{Bài toán 18}}$ Cho tam giác $ABC$ nội tiếp đường tròn $O$. Một đường tròn $(I)$ tiếp xúc với $AB,AC$ và $(O)$ lần lượt tại $K,L,M$. Gọi $N$ là điểm chính giữa cung $BC$ không chứa điểm $A$. Chứng minh rằng $KL,BC,MN$ đồng quy.

 

Spoiler

14440

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:42
Sửa đánh số

[The Collection]

$2$ bài toán trên không khó, mình tìm được lời giải và đang đợi nguyenthehoan ^^, tuy nhiên, bài toán 18 đã có ở link đây, xin trích dẫn:

 

Lời giải của anh Hân (perfectstrong)

 

Đây là lời giải với TH $(X)$ nằm trong $(I)$.
Lời giải:
Nếu $\vartriangle ABC$ cân tại $A$ thì $RT \to$ tiếp tuyến $xy$ tại $T$ của $(I)$. Dễ thấy khi đó $QP,BC,xy$ đôi một song song.
Xét TH $\vartriangle ABC$ không cân tại $A$.
Gọi $(X)$ là đường tròn đi qua $P,Q,R$.Vẽ $RQ,RP$ thứ tự cắt $(I)$ lần thứ 2 tại $F,E$.
Nhận xét 1: $E,F$ thứ tự là trung điểm cung $AC,AB$.
==================================================
$CF,BE$ cắt nhau tại $J$. Từ nhận xét 1, suy ra $BE,CF$ là phân giác $\angle ABC,\angle ACB$ tương ứng. Do đó, $J$ là tâm đường tròn nội tiếp $\vartriangle ABC$.
Nhận xét 2: $PQ$ đi qua $J$ (định lý Lyness)
Chứng minh nhận xét 2:
Áp dụng định lý Pascal cho 6 điểm $(R,F,C,A,B,E)$ có $RF \cap AB=Q; FC \cap BE=J; CA \cap RE=P$, ta có ngay $P,I,Q$ thẳng hàng.
==================================================
Nhận xét 3: $T$ là tâm đường tròn ngoại tiếp $\vartriangle JBC$. Gọi đó là đường tròn $(T)$.
==================================================
Vẽ đường kính $AA_1$ của $(I)$. $JA_1$ cắt $(I)$ lần 2 tại $A_2 \Rightarrow \angle JA_2A=90^o$.
Gọi $(K)$ là đương tròn ngoại tiếp $\vartriangle JA_2A \Rightarrow K$ là trung điểm $JA$ nên $K,J,T$ thẳng hàng.
Do đó, $(K)$ tiếp xúc với $(T)$. Gọi $Jx$ là trục đẳng phương của $(K),(T)$.
Mà ta cũng có $A_2A;BC$ thứ tự là trục đẳng phương của cặp đường tròn $((K);(I));((T);(I))$ nên $BC,A_2A,Jx$ đồng quy
($BC,A_2A;Jx$ không thể đôi một song song vì $AB \ne AC \Rightarrow I \not \in AT \Rightarrow I,K,T$ không thẳng hàng).
Vẽ $BC$ cắt $A_2A$ tại $D \quad (i) \Rightarrow DJ \perp AT$
Từ nhận xét 2, dễ thấy rằng $PQ \perp AT$ tại $J \Rightarrow PQ$ đi qua $D$. (ii)

===================================================
Ta chỉ cần chứng minh $RT$ đi qua $D$ (iii)
Nhận xét 4: $\angle JRT=90^o$
Vẽ đường kính $TS$ của $(I)$. Ta sẽ chứng minh $R,J,S$ thẳng hàng. Gọi $R$ là bán kính của $(I)$.
Ta có:\[ \begin{array}{l} XQ = XR = AQ\tan \frac{{BAC}}{2} \\ JX = JQ\tan JQX = \left( {AQ\sin \frac{{BAC}}{2}} \right)\tan \frac{{ABC}}{2} \\ TJ = TB = 2R\sin \frac{{BAC}}{2} \\ \Rightarrow \frac{{\overline {RX} }}{{\overline {RI} }}.\frac{{\overline {SI} }}{{\overline {ST} }}.\frac{{\overline {JT} }}{{\overline {JX} }} = \frac{{RX}}{{RI}}.\frac{{SI}}{{ST}}.\frac{{JT}}{{JX}} = \frac{{AQ\tan \frac{{BAC}}{2}}}{R}.\frac{1}{2}.\frac{{2R\sin \frac{{BAC}}{2}}}{{\left( {AQ\sin \frac{{BAC}}{2}} \right)\tan \frac{{ABC}}{2}}} = 1 \\ \end{array} \]
Theo định lý Menelaus đảo cho $\vartriangle TXI$, ta có $R,J,S$ thẳng hàng. Suy ra $\angle JRT=\angle SRT=90^o$.

Gọi $(L)$ là đường tròn ngoại tiếp $\vartriangle JRT \Rightarrow L$ là trung điểm $JT$, nên $K,J,L$ thẳng hàng.
Do đó $(K)$ tiếp xúc $(L)$. Mà $JD$ là tiếp tuyến của $(K)$ nên $JD$ cũng là trục đẳng phương của $(K),(L)$.
Mặt khác, $A_2A, RT$ thứ tự là trục đẳng phương của cặp đường tròn $((K);(I));((L);(I))$ và $A_2A;JD$ cắt nhau tại $D$.
Suy ra $RT$ qua D. (iii) được chứng minh.
===================================================
Từ (i),(ii),(iii), ta có đpcm.


Điều đặc biệt: Kể cả khi $(X)$ nằm ngoài $(I)$, bài toán vẫn đúng nếu $T$ là giao điểm thứ 2 của $AX$ và $(I)$.
Chứng minh TH2:
Khi $(X)$ nằm ngoài $(I)$, chứng minh trên vẫn không thay đổi gì nhiều. Chỉ thay đổi 3 điều nhỏ, không ảnh hưởng đến cả bài toán:
1. $E$ là trung điểm cung $ABC$ và $F$ là trung điểm cung $ACB$.
2. $J$ là tâm đường tròn bàng tiếp $\angle BAC$ của $\vartriangle BAC$
3. \[
\frac{{\overline {RX} }}{{\overline {RI} }}.\frac{{\overline {SI} }}{{\overline {ST} }}.\frac{{\overline {JT} }}{{\overline {JX} }} = \left( { - \frac{{RX}}{{RI}}} \right).\frac{{SI}}{{ST}}.\left( { - \frac{{JT}}{{JX}}} \right) = \frac{{RX}}{{RI}}.\frac{{SI}}{{ST}}.\frac{{JT}}{{JX}}
\]

 

 

Lời giải của tranminhbao2607:

 

 

 

Gọi $P$ là giao điểm của $BC$ và $RT$, $X,Y$ lần lượt là giao điểm của $RE,RF$ với $(ABC)$.

 

Ta có: $X,Y$ lần lượt là điểm chính giữa của cung $AB, AC$, và $I$ thuộc $EF$ (trong chứng minh của anh Hân đã nhắc tới $2$ điều này), rõ ràng $BY,CX$ cắt nhau tại $I$

 

Áp dụng định lý Pascal cho lục giác nôi tiếp $RTABCX$, ta được $I,E,P$ thẳng hàng, tức là $P \in EF$, và đó là điều phải chứng minh. 

 

_______

 

P/S: Hoàn có cách khác không nhỉ ^^

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:42

[hungchng]

Xin gởi tiếp mẫu cho HH, tôi dùng trực tiếp các hình đã đưa lên diễn đàn

http://online.print2...9b7edcec0fac94b

 HHMathLinks.rar   385.72K   403 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi hungchng: 04-05-2013 - 09:57

[NLT]

Xin gởi tiếp mẫu cho HH, tôi dùng trực tiếp các hình đã đưa lên diễn đàn

HHMathLinks.rar

 

Vì em chưa có kinh nghiệm làm những kiểu như thế này, em xin nhờ thầy Hùng biên soạn giúp phần hình học được không ạ, em sẽ bổ sung các hình. Em chưa học $\LaTeX$ ạ, em sẽ cố gắng hoàn thành Topic 100 bài trong thời gian sớm nhất, em xin cảm ơn thầy

Bài viết đã được chỉnh sửa nội dung bởi NLT: 30-04-2013 - 10:37

[nguyenthehoan]

$\boxed{\text{Bài toán 17}}$ Cho $PQ$ là một đường kính của đường tròn $(O)$, $A,B$ là $2$ điểm bất kì thuộc $(O)$ sao cho $A,B$ nằm cùng một nửa mặt phẳng bờ $PQ$. Gọi $C$ là giao điểm của $2$ tiếp tuyến tại $A,B$ của $(O)$. Tiếp tuyến tại $Q$ của $(O)$ cắt $PA,PB,PC$ lần lượt tại $A',B',C'$. Chứng minh rằng $C'$ là trung điểm của $A'B'$.

 

Spoiler

15088

 

$\boxed{\text{Bài toán 18}}$ Cho tam giác $ABC$ nội tiếp đường tròn $O$. Một đường tròn $(I)$ tiếp xúc với $AB,AC$ và $(O)$ lần lượt tại $K,L,M$. Gọi $N$ là điểm chính giữa cung $BC$ không chứa điểm $A$. Chứng minh rằng $KL,BC,MN$ đồng quy.

 

Spoiler

14440

 

Bài 17)Giả sử thứ tự trên đường tròn là $P,A,B,Q$

 

Gọi $D$ là giao điểm của $CP$ và $(O)$.Ta có ngay tứ giác $PADB$ điều hòa.

 

Vẽ tiếp tuyến tại $Px$ của $(O)$

 

Xét chùm tia gốc $P$:$Px,PD,PA,PB$ chung gốc $P$ trên $(O)$ và khi chiếu chúng lên $(O)$ ta được tứ giác 

 

điều hòa $PADB$ nên 

 

$P(Px,PD,PA,PB)=-1$.

 

Ta có $Qy$ là tiếp tuyến tại $Q$ nên $Qy//Px$.

 

Áp dụng định lí về chùm điều hòa ta có ngay $C'$ là trung điểm của $A'B'$

 

####)Ý tưởng mới cho bài 18...

 

 

Theo định lí Lyness, ta có ngay $K,J,L$ thẳng hàng với $J$ là tâm nội tiếp tam giác $ABC$.

 

Hơn nữa $KL\perp AJ$.Và hiển nhiên ta cần tới bổ đề $MK,ML$ đi qua trung điểm các cung $AB,AC$

 

Ta có $\widehat{KJB}=\widehat{KMB}=\frac{\widehat{ACB}}{2}$

 

Nên $KJMB$ nội tiếp.Suy ra $\widehat{JMB}=\widehat{AKL}$

 

Tương tự $\widehat{JMC}=\widehat{ALK}\Rightarrow \widehat{BMJ}=\widehat{CMJ}$

 

Hay $MJ$ đi qua chính giữa cung $BC$ chứa $A$.

 

Suy ra $\widehat{NMJ}=90^{\circ}$

 

Gọi $D$ là giao điểm của $KL$ và $MN$ ta có tam giác $DJN$ vuông tại $J$ có đường cao $JM$ nên

 

$DJ^{2}=\overline{DM}.\overline{DN}$.Mà ta có $DJ$ là tiếp tuyến từ $D$ đến $(JBC)$ (vì $N$ chính là tâm 

 

ngoại tiếp tam giác $JBC$)

 

Suy ra $P_{D/(ABC)}=P_{D/(JBC)}$  ($P$ là kí hiệu phương tích)

 

Từ đó suy ra $D$ thuộc trục đẳng phương của $(ABC)$ và $(JBC)$.Hay $D,$ thuộc $BC$.

 

Kết thúc chứng minh....

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:43
Sửa đánh số

[perfectstrong]

Vì em chưa có kinh nghiệm làm những kiểu như thế này, em xin nhờ thầy Hùng biên soạn giúp phần hình học được không ạ, em sẽ bổ sung các hình. Em chưa học $\LaTeX$ ạ, em sẽ cố gắng hoàn thành Topic 100 bài trong thời gian sớm nhất, em xin cảm ơn thầy

Phần Hình học thì có thể anh giúp được.

Rất cảm ơn thầy Hùng đã đóng góp mẫu

 

@NLT: Anh Hân giúp được thì tốt quá

Bài viết đã được chỉnh sửa nội dung bởi NLT: 30-04-2013 - 15:18

[NLT]

^^ Bài 16 tớ cũng giải như cậu, thế là bài 17 ta đã có 3 cách giải

 

Tiếp tục nào:

 

$\boxed{\text{Bài toán 19}}$ Cho $\Delta ABC$. $A'$ là trung điểm của $BC$. $T_a$ là tiếp điểm của đường tròn nội tiếp tam giác với $BC$. Vẽ đường tròn tâm $A'$ đi qua $T_a$. Định nghĩa tương tự với $(B'),(C')$. Chứng minh rằng nếu $(A')$ tiếp xúc với đường tròn ngoại tiếp $\Delta ABC$ thì $(B')$ hoặc $(C')$ cũng tiếp xúc với đường tròn ngoại tiếp $\Delta ABC$. 

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:44
Sửa đánh số

[The Collection]

^^ Bài 16 tớ cũng giải như cậu, thế là bài 17 ta đã có 3 cách giải

 

Tiếp tục nào:

 

$\boxed{\text{Bài toán 19}}$ Cho $\Delta ABC$. $A'$ là trung điểm của $BC$. $T_a$ là tiếp điểm của đường tròn nội tiếp tam giác với $BC$. Vẽ đường tròn tâm $A'$ đi qua $T_a$. Định nghĩa tương tự với $(B'),(C')$. Chứng minh rằng nếu $(A')$ tiếp xúc với đường tròn ngoại tiếp $\Delta ABC$ thì $(B')$ hoặc $(C')$ cũng tiếp xúc với đường tròn ngoại tiếp $\Delta ABC$. 

 

Lời giải của tranminhbao2607:

 

 

Ta chứng minh bài toán sau: Ta chứng minh góc $\angle B$ hoặc $\angle C$ là góc vuông.

 

Thật vậy, từ đề ra, ta có: 

\[A'{T_a} + OA' = R \Leftrightarrow \frac{{\left| {b - c} \right|}}{2} + \sqrt {{R^2} - \frac{{{a^2}}}{4}}  = R\]\[ \Leftrightarrow |\sin B - \sin C| + \sqrt {1 - {{\sin }^2}\frac{A}{2}}  = 1 \Leftrightarrow |\sin B - \sin C| = 1 - \cos A\]\[ \Leftrightarrow 2\cos \frac{{B + C}}{2}\sin \frac{{\left| {B - C} \right|}}{2} = 2{\sin ^2}\frac{A}{2} \Leftrightarrow \sin |B - C| = \sin A\] \[ |B-C|=A \to \angle B = 90^o \vee \angle C= 90^o\]

 

Để ý rằng các phép biến đổi trên đều là biến đổi tương đương, vì thế, với kết quả $\angle B$ hoặc $\angle C$ vuông ta cũng suy ra $(B')$ hoặc $(C')$ tiếp xúc với đường tròn ngoại tiếp tam giác $ABC$.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:44

[nguyenthehoan]

 

Lời giải của tranminhbao2607:

 

Ảnh chụp màn hình_2013-04-30_203526.png

 

Ta chứng minh bài toán sau: Ta chứng minh góc $\angle B$ hoặc $\angle C$ là góc vuông.

 

Thật vậy, từ đề ra, ta có: 

\[A'{T_a} + OA' = R \Leftrightarrow \frac{{\left| {b - c} \right|}}{2} + \sqrt {{R^2} - \frac{{{a^2}}}{4}}  = R\]\[ \Leftrightarrow |\sin B - \sin C| + \sqrt {1 - {{\sin }^2}\frac{A}{2}}  = 1 \Leftrightarrow |\sin B - \sin C| = 1 - \cos A\]\[ \Leftrightarrow 2\cos \frac{{B + C}}{2}\sin \frac{{\left| {B - C} \right|}}{2} = 2{\sin ^2}\frac{A}{2} \Leftrightarrow \sin |B - C| = \sin A\] \[ |B-C|=A \to \angle B = 90^o \vee \angle C= 90^o\]

 

Để ý rằng các phép biến đổi trên đều là biến đổi tương đương, vì thế, với kết quả $\angle B$ hoặc $\angle C$ vuông ta cũng suy ra $(B')$ hoặc $(C')$ tiếp xúc với đường tròn ngoại tiếp tam giác $ABC$.

 

Một cách khác "hình học hơn"..Gọi $S$ là điểm chính giữa cung nhỏ $BC$.

 

 

Theo bài ra ta dễ dàng có: $\Delta SA'T_{a}$ vuông cân.

 

Giả sử $AB<AC$ ta có $\widehat{ST_{a}B}=135^{\circ}$

 

Theo một bổ đề quen biết thì $SI=SB$ với $I$ là tâm nội tiếp tam giác $ABC$

 

Từ đó ap dụng định lí hàm số cos cho các tam giác $ST_{a}I$ và $ST_{a}B$ ta có 

 

$ST_{a}^{2}+T_{a}B^{2}+\frac{\sqrt{2}}{2}ST_{a}.T_{a}B=ST_{a}^{2}+T_{a}I^{2}+\frac{\sqrt{2}}{2}ST_{a}.T_{a}I$

 

(Chú ý các góc $135 độ$)

 

Chuyển vế ta có ngay $T_{a}I=T_{a}B$ Do đó $\widehat{ABC}=90^{\circ}$

 

Done

[nguyenthehoan]

Lâu lâu ko làm bất đẳng thức hình...

 

$\boxed{\text{Bài toán 20}}$ Cho $\Delta ABC$ đều cạnh bằng $\sqrt{3}$.$M$ là điểm bất kì di động

 

trong mặt phẳng tam giác.

 

Chứng minh rằng:$MA^{2}+MB^{2}+MC^{2}\leq MA^{2}.MB^{2}+MB^{2}.MC^{2}+MC^{2}.MA^{2}$

 

$\boxed{\text{Bài toán 21}}$ Với $P$ là điểm bất kì chạy trong mặt phẳng chứa $\Delta ABC$,Tìm vị trí của

 

$P$ để biểu thức 

 

$P=PA.PB+PB.PC+PC.PA$ đạt GTNN.Tính giá trị nhỏ nhất đó.

 

P/S:Hai bài khá dễ...Cái hay là tổng quát chúng

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:44
Sửa đánh số

[Ispectorgadget]

Bài toán 21: Với $P$ là điểm bất kì chạy trong mặt phẳng chứa $\Delta ABC$,Tìm vị trí của

 

$P$ để biểu thức 

 

$P=PA.PB+PB.PC+PC.PA$ đạt GTNN.Tính giá trị nhỏ nhất đó.

 

P/S:Hai bài khá dễ...Cái hay là tổng quát chúng

Tổng quát bài này : China 1998
Cho $P$ là 1 điểm bất kì trong tam giác nhọn $ABC$ với độ dài các cạnh là $BC=a,CA=b,AB=c$. Đặt $PA=x,PB=y,PC=z$. Chứng minh $ayz+bxz+cxy\ge abc$

Dấu bằng xảy ra khi và chỉ khi $P$ là tâm đường tròn ngoại tiếp tam giác $ABC.$

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:45
Sửa đánh số

[NLT]

Tổng quát bài này : China 1998
Cho $P$ là 1 điểm bất kì trong tam giác nhọn $ABC$ với độ dài các cạnh là $BC=a,CA=b,AB=c$. Đặt $PA=x,PB=y,PC=z$. Chứng minh $ayz+bxz+cxy\ge abc$

Dấu bằng xảy ra khi và chỉ khi $P$ là tâm đường tròn ngoại tiếp tam giác $ABC.$

 

Tiện thể anh Kiên đưa ra lời giải được không ạ? Đang rất gấp , tiến đến con số $100$ nào

[Ispectorgadget]

Cho $P$ là 1 điểm bất kì trong tam giác nhọn $ABC$ với độ dài các cạnh là $BC=a,CA=b,AB=c$. Đặt $PA=x,PB=y,PC=z$. Chứng minh $ayz+bxz+cxy\ge abc$

Dấu bằng xảy ra khi và chỉ khi $P$ là tâm đường tròn ngoại tiếp tam giác $ABC.$

 

Giả sử $D$ là điểm gốc của mặt phẳng phức và gọi tọa độ phức của các điểm $A,B,C$ lần lượt là $u,v\omega$. Ta viết lại BĐT trên dưới dạng số phức $$|uv(u-v)|+|v\omega(v-\omega)|+|\omega u(\omega-u)\ge |(u-v)(v-\omega)(\omega-u).|$$

Dễ dàng kiểm chứng đẳng thức $$uv(u-v)+v\omega(v-\omega)+\omega u(\omega-u)=-(u-v)(v-\omega)(\omega-u)$$

Việc còn lại ta xác định khi nào đẳng thức xảy ra . Đặt $$z_1=\frac{uv}{(u-\omega)(v-\omega)};z_2=\frac{v\omega}{(v-u)(\omega-u)};z_3=\frac{\omega u}{(\omega-v)(u-v)}$$

Với cách đặt trên ta viết lại BĐT trên thành $$|z_1|+|z_2|+|z_3|\ge 1; z_1+z_2+z_3=1$$

Vậy đẳng thức xảy ra khi và chỉ khi $z_1,z_2,z_1$ là các số thực dương.
Giả sử $z_1,z_2,z_3$ là các số thực dương. Vì  $$\frac{-z_1.z_2}{z_3}=\left(\frac{v}{\omega-u} \right )^2;\frac{-z_3.z_2}{z_1}=\left(\frac{\omega}{v-u} \right )^2;\frac{-z_1.z_3}{z_2}=\left(\frac{u}{v-\omega} \right )^2$$

 

Từ số phức $\frac{u}{v-\omega}$ có bình phương là 1 số thực âm nên là các số thuần ảo; vậy góc tạo bởi các vecteur biểu diễn $u$ là $\overrightarrow{AD}$ và vecteur biểu diễn $v-\omega$ là $\overrightarrow{BC}$ có số đo góc $90^0$, suy ra $AD$ vuông góc $BC$. Tương tự $\frac{v}{\omega-u}$ là số thuần ảo suy ra $BD$ vuông góc $AC$. Vậy $D$ là trực tâm tam giác $ABC$

 

Điểm $D$ trong tam giác và $AD$ vuông góc $BC$ nên góc tạo bởi các véc tơ $AD,BC$ có số đo là $-90^0$, suy ra tồn tại số thực dương $r_1$ sao cho $\frac{u}{v-\omega}=-r_1i$.

Tương tự tồn tại số thực dương $r_2,r_3$ sao cho $\frac{v}{\omega-u}=-r_2i;\frac{\omega}{u-v}=-r_3i$. Vậy $z_1,z_2,z_3$ là các số thực dương.

Từ các kết quả trên ta có kết luận đẳng thức xảy ra khi và chỉ khi $D$ là trực tâm tam giác $ABC$.

 

===

Bài này còn 1 cách dùng BĐT Ptolemé.

[nguyenthehoan]

Tổng quát bài này : China 1998
Cho $P$ là 1 điểm bất kì trong tam giác nhọn $ABC$ với độ dài các cạnh là $BC=a,CA=b,AB=c$. Đặt $PA=x,PB=y,PC=z$. Chứng minh $ayz+bxz+cxy\ge abc$

Dấu bằng xảy ra khi và chỉ khi $P$ là tâm đường tròn ngoại tiếp tam giác $ABC.$

Đây đúng là China98,Nhưng hình như kết quả trên ko áp dụng được vào bài này thì phải

[NLT]

Lại một bài nữa về đường tròn nội tiếp

 

$\boxed{\text{Bài toán 22}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(I)$, gọi $O_A, O_B,O_C$ lần lượt là giao điểm của các đường phân giác góc $\angle A, \angle B, \angle C$ với $(I)$. Gọi $(O_A)$ là đường tròn tâm $O_A$ và tiếp xúc với $AB,AC$. Định nghĩa tương tự với $(O_B),(O_C)$. Gọi $t_A$ là tiếp tuyến chung ngoài của $(O_B)$ và $(O_C)$, định nghĩa tương tự với $t_B, t_C$. Chứng minh rằng $t_A, t_B,t_C$ đồng quy.

[49192]

 

Và một vấn đề quen thuộc nhưng hoàn toàn không hề cũ

 

$\boxed{\text{Bài toán 23}}$ Cho $\omega_1$ và $\omega_2$ với các bán kính $r_1,r_2$ thỏa $r_2>r_1$ tiếp xúc ngoài với nhau. $t_1$ tiếp xúc với $\omega_1, \omega_2$ lần lượt tại $A,D$. Kẻ $t_2 // t_1$ và tiếp xúc với $\omega_1$, nó cắt $\omega_2$ lần lượt tại $E,F$. Kẽ $t_3$ đi qua $D$  cắt $t_2, \omega_2$ lần lượt tại $B,C$ (khác $E,F$ tương ứng). Chứng minh rằng đường tròn ngoại tiếp của $\Delta ABC$ tiếp xúc với $t_1$.

[53277]

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:45

[nguyenthehoan]

Lại một bài nữa về đường tròn nội tiếp

 

$\boxed{\text{Bài toán 22}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(I)$, gọi $O_A, O_B,O_C$ lần lượt là giao điểm của các đường phân giác góc $\angle A, \angle B, \angle C$ với $(I)$. Gọi $(O_A)$ là đường tròn tâm $O_A$ và tiếp xúc với $AB,AC$. Định nghĩa tương tự với $(O_B),(O_C)$. Gọi $t_A$ là tiếp tuyến chung ngoài của $(O_B)$ và $(O_C)$, định nghĩa tương tự với $t_B, t_C$. Chứng minh rằng $t_A, t_B,t_C$ đồng quy.

[49192]

 

Và một vấn đề quen thuộc nhưng hoàn toàn không hề cũ

 

$\boxed{\text{Bài toán 23}}$ Cho $\omega_1$ và $\omega_2$ với các bán kính $r_1,r_2$ thỏa $r_2>r_1$ tiếp xúc ngoài với nhau. $t_1$ tiếp xúc với $\omega_1, \omega_2$ lần lượt tại $A,D$. Kẻ $t_2 // t_1$ và tiếp xúc với $\omega_1$, nó cắt $\omega_2$ lần lượt tại $E,F$. Kẽ $t_3$ đi qua $D$  cắt $t_2, \omega_2$ lần lượt tại $B,C$ (khác $E,F$ tương ứng). Chứng minh rằng đường tròn ngoại tiếp của $\Delta ABC$ tiếp xúc với $t_1$.

[53277]

Thịnh xem lại bài 22 giúp tớ nha

 

Bài 23:

 

Gọi $K$ là tiếp điểm của hai đường tròn $\omega _{1},\omega _{2}$.

 

$X$ là tiếp điểm của $\omega _{1}$ với $t_{2}$.Vì $t_{2}//t_{1}$ nên $AX$ là đường kính của $\omega _{1}$

 

Suy ra $D,K,X$ thẳng hàng.

 

Ta có $\widehat{DCK}=\widehat{KDA}=\widehat{DXB}$  (vì $t_{2}//t_{1}$)

 

Nên tứ giác $KBCX$ nội tiếp.Do đó $\overline{DB}.\overline{DC}=\overline{DK}.\overline{DX}=DA^{2}$

 

Suy ra $AD$ tiếp xúc $(ABC)$.Nói cách khác $t_{1}$ tiếp xúc $(ABC)$.Done

P/s: Bài 22 nó không đồng quy mà ra tam giác, Thịnh xem lại giùm!

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:45

[NLT]

Ở mỗi bài toán, khuyến khích nên tổng quát, hoặc bài toán tương tự, hoặc ý tưởng đặc biệt nào đó ngoài việc giải bài  

[nguyenthehoan]

Lại một bài nữa về đường tròn nội tiếp

 

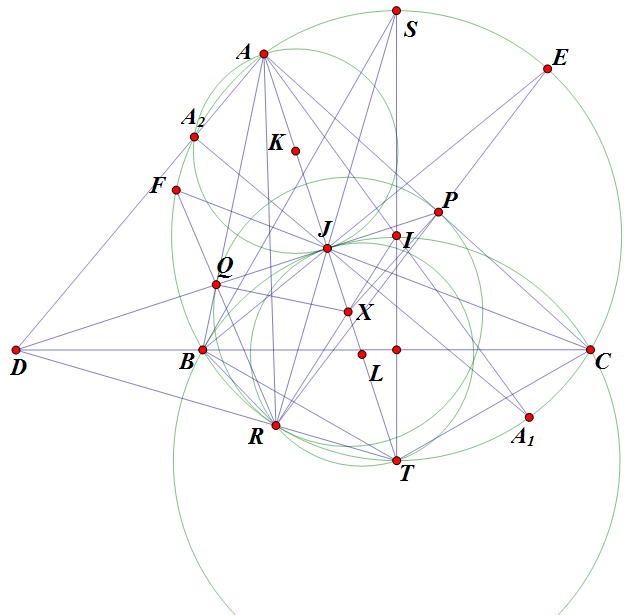
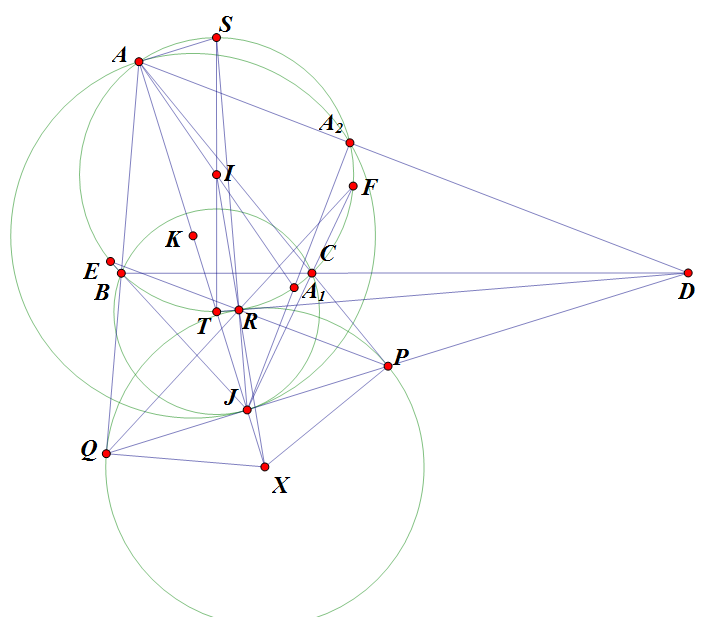
$\boxed{\text{Bài toán 22}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(I)$, gọi $O_A, O_B,O_C$ lần lượt là giao điểm của các đường phân giác góc $\angle A, \angle B, \angle C$ với $(I)$. Gọi $(O_A)$ là đường tròn tâm $O_A$ và tiếp xúc với $AB,AC$. Định nghĩa tương tự với $(O_B),(O_C)$. Gọi $t_A$ là tiếp tuyến chung ngoài của $(O_B)$ và $(O_C)$, định nghĩa tương tự với $t_B, t_C$. Chứng minh rằng $t_A, t_B,t_C$ đồng quy.

[49192]

 

Bài này là :$\Delta ABC$ ngoại tiếp $(I)$...

 

Chứng Minh:Ta cần có 2 bổ đề quen thuộc sau:

 

Bổ đề 1:Cho $\Delta ABC$ ,$D$ và $E$ là các trung điểm cung $BC$,$CA$ không chứa

 

$A,B$.Gọi $X,Y$ là các giao điểm của $DE$ với $BC,CA$.Gọi $I$ là tâm nội tiếp tam giác$ABC$.Khi đó ta có 

 

$IX//AC$ và $IY//BC$. (có thể dễ dàng chứng minh bổ đề này bằng định lí Talet)

 

Bổ đề 2:Cho tam giác$ABC$.$D,E,F$ thứ tự là trung điểm các cung $BC,AC,AB$ (ko chứa đỉnh đối diện).

 

Khi đó các đường chéo chính của lục giác tạo bởi phần giao nhau của hai tam giác $ABC$ và $DEF$ đồng quy tại $I$ là tâm nội 

 

tiếp tam giác $ABC$.  (Suy ra trực tiếp từ bổ đề 1).

 

Trở lại bài toán:

 

Gọi $D,E,F$ là tiếp điểm trên $BC,CA,AB$ của $(I)$.Ta có $\widehat{AFO_{A}}=\widehat{FDO_{A}}=\widehat{O_{A}FE}$

 

(vì $O_{A}$ là trung điểm cung $EF$).Từ đó suy ra $(O_{A})$ là đường tròn nội tiếp tam giác $AEF$.

 

Tương tự với các đường tròn $O_{B},O_{C}$.

 

Gọi $X,Z$ thứ tự là giao điểm của $(O_{B}O_{A},EF),(O_{B}O_{C},DE)$. Ta sẽ chứng minh $XZ$ chính là tiếp tuyến chung 

 

của $(O_{A}),(O_{C})$

 

Gọi $K$ là tâm nội tiếp tam giác $DEF$.Áp dụng bổ đề (1) ta có $KX//FD,KZ//FD$ hay $XZ//FD$

 

Ta phải chứng minh $XZ$ và $FE$ đối xứng nhau qua $O_{A}O_{B}$ 

 

$\Leftrightarrow \widehat{ZXY}=\widehat{FXY}$  ($Y$ là giao của $O_{A}O_{B}$ và $DF$)

 

$\Leftrightarrow \widehat{FXY}=\widehat{FYX}$  (vì $XZ//DF$)

 

Điều này hiển nhiên đúng vì $O_{A},O_{B}$ là trung điểm các cung $EF$ và $DF$ và $\widehat{FXY}=\frac{sd\widehat{O_{A}E}+sd\widehat{FO_{B}}}{2}$

 

Do đó ta có $XZ$ và $EF$ đối xứng qua $O_{A}O_{B}$.Mà $EF$ là tiếp tuyến của $(O_{A})$ nên $XZ$ cũng là tiếp tuyến của $(O_{A})$.

 

Tương tự $XZ$ cũng là tiếp tuyến của $(O_{C})$ nên ta có $XZ$ là tiếp tuyến chung của $(O_{A})$ và $(O_{C})$

 

Tương tự với các tiếp tuyến chung của $(O_{A}),(O_{B})$ và $(O_{C}),(O_{B})$.

 

Cuối cùng áp dụng trực tiếp bổ đề 2 ta có ngay $3$ tiếp tuyến $t_{A},t_{B},t_{C}$ đồng quy tại tâm nội tiếp $\Delta DEF$

 

Done

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:46

[nguyenthehoan]

Khi làm 22 mình phát hiện ra: Một bài toán khá giống hình thức bài 22:  (chắc là dễ hơn )

 

Cho $\Delta ABC$.Các đường cao  $AD,BE.CF$.Gọi $(O_{a})$ là đường tròn nội tiếp $\Delta AEF$.Tương tự xác định các đường 

 

$(O_{b})$,$(O_{c})$.Gọi $t_{a}$ là tiếp tuyến chung khác $BC$ của $(O_{b}),(O_{c})$.Xác định tương tự các đường thẳng 

 

$t_{b},t_{c}$.Chứng minh rằng các đường thẳng $t_{a},t_{b},t_{c}$ đồng quy.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:46

[NLT]

1 mở rộng nữa từ bài $22$: Giao điểm của các đường thẳng đồng quy đó, là tâm đường tròn nội tiếp của $\Delta DFE$, với $D,E,F$ lần lượt là tiếp điểm của đường tròn nội tiếp tam giác $ABC$ với $BC,CA,AB$ 

 

Hoàn chứng minh luôn cái mở rộng này, và post lời giải cho bài toán tương tự kia nhé !

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 07-05-2013 - 22:46