Không phải đâu bạn  ...Mà bài này khá đơn giản..Post tiếp bài nữa...(Mở rộng bài 23)
...Mà bài này khá đơn giản..Post tiếp bài nữa...(Mở rộng bài 23)
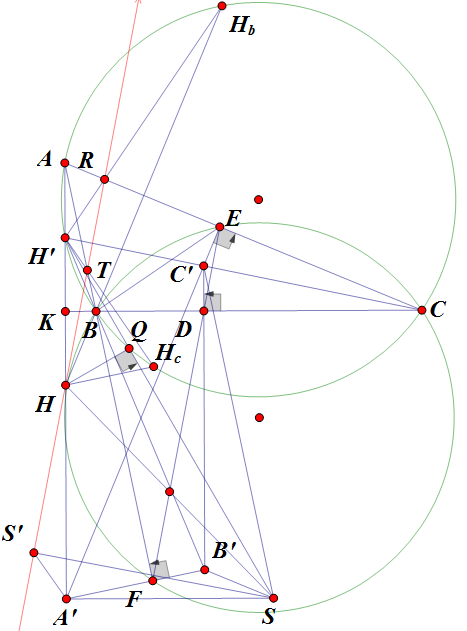
$\boxed{\text{Bài toán 25}}$ Cho tam giác $ABC$.Điểm $E$ thuộc đoạn $AC$,điểm $F$ thuộc tia đối của tia
$BA$ sao cho $AE.AC=AB.AF$.Gọi $D$ là giao điểm của $BC$ và $EF$.Qua $D,E,F$ lần lượt vẽ các đường
thẳng $(l),(t),(k)$ vuông góc với$BC,CA,AB$.Các đường thẳng $(l),(t),(k)$ cắt nhau tạo thành $\Delta A'B'C'$.Gọi
$S$ là trực tâm tam giác $A'B'C'$.Gọi $S'$ là điểm đối xứng của $S$ qua $EF$.Chứng minh rằng $S'$ luôn
thuộc một đường thẳng cố định khi $E,F$ di chuyển.
Mãi mới giải được bài này 
Lời giải:
Ta cần 2 bổ đề sau về tam giác Paralogic.
Bổ đề 1:
Cho $\vartriangle ABC$ và 1 cát tuyến $DEF\, (D\in BC, E\in AC, F \in AB)$. Các đường thẳng $a,b,c$ lần lượt qua $D,E,F$ thứ tự vuông góc $BC,CA,AB$ cắt nhau tại $A',B',C'$ sao cho $a \cap b=C', b \cap c=A', c \cap a=B'$.
Khi đó $(ABC);(A'B'C');AA';BB';CC'$ đồng quy.

Chứng minh bổ đề 1:
Gọi $J$ là giao điểm của $AA',CC'$.
\[
\left( {AB;AJ} \right) \equiv \left( {AF;AA'} \right) \equiv \left( {EF;EA'} \right) \equiv \left( {ED;EC'} \right) \equiv \left( {CD;CC'} \right) \equiv \left( {CB;CJ} \right)\pmod {\pi }
\]
Do đó $J \in (ABC)$. Cho nên\[
\left( {BJ;BC} \right) \equiv \left( {AJ;AC} \right) \equiv \left( {AA';AE} \right) \equiv \left( {FA';FE} \right) \equiv \left( {FB';FD} \right) \equiv \left( {BB;BD} \right)\pmod {\pi }
\]
Suy ra $B,B',J$ thẳng hàng hay $AA',BB',CC'$ đồng quy tại $J$ thuộc $(ABC)$.
Ta cũng có \[
\left( {JC';JA'} \right) \equiv \left( {JC;JA} \right) \equiv \left( {BC;BA} \right) \equiv \left( {BD;BF} \right) \equiv \left( {B'D;B'F} \right) \equiv \left( {B'C';B'A'} \right)\pmod {\pi }
\]
Do đó $J \in (A'B'C')$. Ta có đpcm.
========================================
Bổ đề 2:
Cũng với cấu hình như bổ đề 1. Gọi $H,H'$ thứ tự là trực tâm $\vartriangle ABC,\vartriangle A'B'C'$.
Khi đó $DE$ đi qua trung điểm $HH'$.

Chứng minh bổ đề 2:
Xác định $J$ như trong chứng minh bổ đề 1. Gọi $P,M$ thứ tự là hình chiếu của $J$ lên $AB,AC$ thì $PM$ là đường thẳng Simpson của $J$ đối với $\vartriangle ABC$.
Ta có:\[
\left( {PJ;PM} \right) \equiv \left( {BJ;BM} \right) \equiv \left( {BJ;BC} \right) \equiv \left( {AJ;AC} \right) \equiv \left( {AA';AE} \right) \equiv \left( {FA';FE} \right) \pmod{\pi}
\]
Mà chú ý rằng $PJ \parallel A'F \Rightarrow DE \parallel PM \Rightarrow DE$ song song với đường thẳng Steiner của $J$ ứng với $\vartriangle ABC \Rightarrow DE \parallel HJ_1$, trong đó $J_1$ là điểm đối xứng của $J$ qua $BC$.
Tương tự, $DE \parallel HJ_2$ với $J_2$ là điểm đối xứng của $J$ qua $B'C'$.
$B'C';BC$ thứ tự là trung trực $JJ_2;JJ_1$ mà $BC\perp B'C'$ tại $D$ nên $JJ_1 \perp JJ_2$ và $D$ là trung điểm $JJ_2$.
Do đó $$\overrightarrow{DJ_1}=-\overrightarrow{DJ_2}$$
Gọi $T$ là giao điểm của $DE$ và $HH'$.
Xét phép chiếu theo phương $DE$ lên $HH'$, ta có $\overrightarrow{TH'}=-\overrightarrow{TH}$.
Suy ra $T$ là trung điểm $HH'$. Ta có đpcm.
========================================

Quay lại bài toán. Gọi $H$ là trực tâm $\vartriangle ABC$.
Áp dụng bổ đề 2, ta có $DE$ đi qua trung điểm $HS$.
Mà $DE$ cũng đi qua trung điểm $SS'$ nên $DE$ là đường trung bình $\vartriangle SHS'$.
Suy ra $HS' \parallel DE$.
Mặt khác, từ giả thiết $AE.AC=AB.AF$, ta có $BECF$ là tứ giác nội tiếp. Nên
$$(ED;EC) \equiv (EF;EC) \equiv (BF;BC) \equiv (BA;BC) \pmod{\pi}$$
Do đó $(HS';AC) \equiv (ED;EC) \equiv (BA;BC) \pmod{\pi}$.
$H,A,C,B$ cố định nên $S'$ chạy trên đường thẳng $a$ cố định qua $H$ sao cho $(a;AC)\equiv (BA;BC) \pmod{\pi}$.
Ta có đpcm.
Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 20-05-2013 - 20:20
)