Chủ đề này có 159 trả lời

[nguyenthehoan]

Ủng hộ topic của Thịnh một bài.

 

$\boxed{\text{Bài toán 9}}$ Cho $\Delta ABC$ ngoại tiếp đường tròn $(I)$. Gọi $M, N, P$ thứ tự là trung điểm của $BC, CA, AB$.

Qua M vẽ tiếp tuyến với $(I)$, cắt $NP$ tại $X$. Các điểm $Y,Z$ xác định tương tự trên $PM$, $MN$.

Chứng minh rằng $X,Y,Z$ thẳng hàng.

 

[nguyenthehoan]

Mình gợi ý bài này $X,Y,Z$ cùng nằm trên trục đẳng phương của $(I)$ và đường tròn nội tiếp $\Delta MNP$

 

Các bạn thử làm xem!!!

[NLT]

Ủng hộ topic của Thịnh một bài.

 

$\boxed{\text{Bài toán 9}}$ Cho $\Delta ABC$ ngoại tiếp đường tròn $(I)$. Gọi $M, N, P$ thứ tự là trung điểm của $BC, CA, AB$.

Qua M vẽ tiếp tuyến với $(I)$, cắt $NP$ tại $X$. Các điểm $Y,Z$ xác định tương tự trên $PM$, $MN$.

Chứng minh rằng $X,Y,Z$ thẳng hàng.

 

Nhờ gợi ý của Hoàn, xin trình bày lời giải vắn tắt:

 

 

 

 

 

 

 

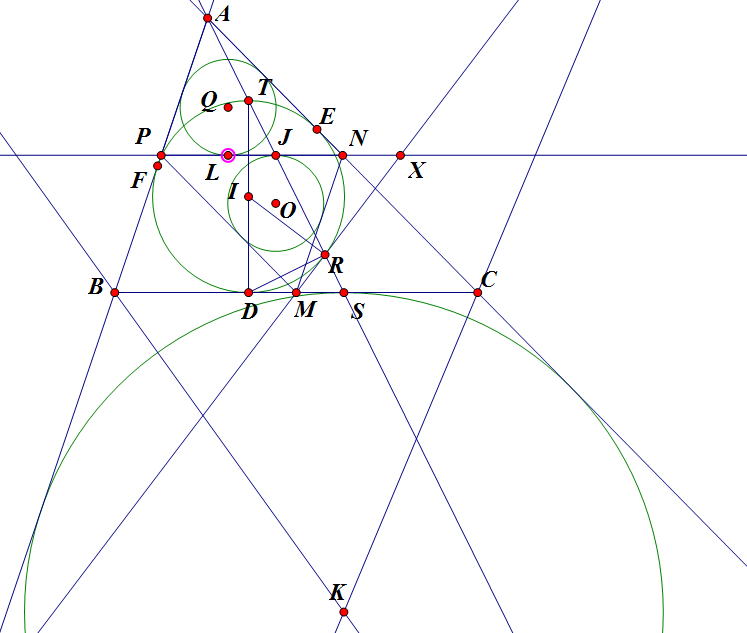
Gọi $S$ là giao điểm của $AT$ và $BC$ với $T$ là điểm thuộc $(I)$ sao cho $DI$ là đường kính của $(I)$.

 

Dựng đường tròn bàng tiếp góc $\angle A$ của $\Delta ABC$, khi đó, dễ thấy, qua phép vị tự tâm $A$ tỉ số $\frac{AI}{AK}$ thì $ (I) \to (K); T \to S$

 

Nên $S$ là tiếp điểm của tiếp tuyến tại $C$ của $(K)$. Không khó để suy ra $CS=BD (=p-a)$.

 

Do $M$ là trung điểm $BC$ nên $M$ là trung điểm của $DS$, giả sử $AS$ cắt $(I)$ tại điểm thứ $2$ là $R$, khi đó $\Delta DRS$ vuông tại $R$, có $M$ là trung điểm nên $MD=MR$, lại có $MD$ là tiếp tuyến tại $D$ của $(I)$, nên $MR$ là tiếp tuyến của $(I)$, do đó $X$ là giao điểm của $MR$ và $NP$.

 

Dựng $(Q)$ nội tiếp tam giác $\Delta APN$, $L$ là tiếp điểm của $PN$ với $(Q)$, rõ ràng qua phép vị tự tâm $A$ tỉ số $\frac{AI}{AQ}$, biến $(I) \to (Q)$, từ đó cũng biến $(K) \to (O); S \to J$, do đó $J$ là tiếp điểm của $PN$ với đường tròn $(O)$.

 

Để ý rằng: $\Delta MRS \sim \Delta XRJ \to XR=XJ \to X$ nằm trên trục đẳng phương của $(I)$ và đường tròn nội tiếp $\Delta MNP$, tương tự ta cũng có $Y,Z$ nằm trên đường đó, cuối cùng có $Q.E.D$.

 

 

P/s: To nguyenthehoan: Bài này quá hay ^^, tks cậu đã gợi ý Vấn đề: Liệu có thể thay đổi tỉ số $M,N,P$ trên $BC,CA,AB$, không phải trung điểm nữa? 

Bài viết đã được chỉnh sửa nội dung bởi NLT: 13-04-2013 - 21:34

[ht2pro102]

$\boxed{\text{Bài toán 10}}$ Cho $\Delta ABC$ có đường tròn tâm $(I)$ nội tiếp, tiếp xúc với các cạnh $BC,CA,AC$ lần lượt tại $D,E,F$. Trung tuyến $AM$ cắt $EF$ tại $J$.Chứng minh : $D,I,J$ thẳng hàng.

Bài viết đã được chỉnh sửa nội dung bởi NLT: 14-04-2013 - 17:01

[NLT]

$\boxed{\text{Bài toán 10}}$ Cho $\Delta ABC$ có đường tròn tâm $(I)$ nội tiếp, tiếp xúc với các cạnh $BC,CA,AC$ lần lượt tại $D,E,F$. Trung tuyến $AM$ cắt $EF$ tại $J$.Chứng minh : $D,I,J$ thẳng hàng.

 

Bài toán này không khó, bạn có thể nhắn tin cho mình link của nó trên Mathlinks.ro không?

 

Giải như sau:

 

 

 

Gọi $J'$ là giao điểm của $DI$ và $EF$, qua $I$ kẻ đưởng thẳng song song với $BC$ cắt $AB,AC$ lần lượt tại $P,N$. Ta chứng minh $J \equiv J'$ hay cần chứng minh $J' \in AM$. 

 

Như vậy đưa đến việc chứng minh: $J'$ là trung điểm của $PN$, từ đó theo định lý Thales có ngay $J' \in AM$.

 

Để ý rằng $FJ'E$ là đường thẳng Simson của $\Delta APN \to I, A,P,Q$ đồng viên.

 

Mà $AI$ là phân giác của góc $\angle PAN \to IP=IN \to J'$ là trung điểm của $PN$, và dẫn đến điều phải chứng minh!

Bài viết đã được chỉnh sửa nội dung bởi NLT: 14-04-2013 - 17:17

[NLT]

Mở rộng bài toán 10:

 

Không phải điểm $I$ là tâm đường tròn nội tiếp nữa, cho $I$ chạy bất kì trên $AD$, Kẽ $IM,IN,IP$ lần lượt vuông góc $AB,BC,CA$, khi đó $AK,MP,IM$ đồng quy, với $K$ là trung điểm của $BC$. Chứng minh hoàn toàn tương tự. 

[NLT]

Lưu ý: Các bạn khi post bài phải nhắn tin cho mình link bài toán đó tại Mathlinks.ro, vì có nhiều bạn không đọc Tiêu đề, nội dung của Topic này mà vào post bài không nằm trên Mathlinks.ro. Cảm ơn !

[WhjteShadow]

$\boxed{ \text{Bài toán 11}}$

Ch0 $H,K,I$ lần lượt là chân đường ca0 hạ từ $A,B,C$ của $\Delta ABC$. $M,N$ là hình chiếu của $K$ xuống $AI$ và $I$ xuống $AK$. Lấy $P,Q$ trên $HI,HK$ sa0 ch0 $AP,AQ$ lần lượt vuông góc với $HI,HK$.

Chứng minh rằng $M,N,P,Q$ đồng viên

Bài viết đã được chỉnh sửa nội dung bởi NLT: 30-04-2013 - 09:33

[BlackSelena]

Mở rộng bài toán 10:

 

Không phải điểm $I$ là tâm đường tròn nội tiếp nữa, cho $I$ chạy bất kì trên $AD$, Kẽ $IM,IN,IP$ lần lượt vuông góc $AB,BC,CA$, khi đó $AK,MP,IM$ đồng quy, với $K$ là trung điểm của $BC$. Chứng minh hoàn toàn tương tự. 

$IN$ cắt $MP$ tại $H$, đường thẳng qua $H$ vuông góc với $NH$ cắt 2 cạnh tam giác tại $L,K$ như hình. Khi đó ta có $LHIM; HPKI:tngt$, vậy:
$\angle ILH = \angle IMH = \angle IPH = \angle HKI$

$\Rightarrow LH = HK$

Vậy theo bổ đề hình thang thì $\overline{A,H,M}$

[nguyenthehoan]

$\boxed{ \text{Bài toán 11}}$

Ch0 $H,K,I$ lần lượt là chân đường ca0 hạ từ $A,B,C$ của $\Delta ABC$. $M,N$ là hình chiếu của $K$ xuống $AI$ và $I$ xuống $AK$. Lấy $P,Q$ trên $HI,HK$ sa0 ch0 $AP,AQ$ lần lượt vuông góc với $HI,HK$.

Chứng minh rằng $M,N,P,Q$ đồng viên

Nếu đề đúng phải là $M,N,P,Q$ thẳnh hàng chứ Đạt

 

Ta có $AQHP$ nội tiếp nên $\widehat{AQP}=\widehat{AHP}=\widehat{ACI}=\widehat{AKM}=\widehat{AQM}$

 

Vì vậy $Q,P,M$ thẳng hàng.

 

Tương tự ta cũng có $P,Q,N$ thẳng hàng.

 

Do đó $M,N,P,Q$ thẳng hàng.

------

Her her tr0ng file của t nó ghi là đồng viên :@)

Bài viết đã được chỉnh sửa nội dung bởi WhjteShadow: 19-04-2013 - 09:30

[Oral1020]

$\boxed{\text{Bài toán 12}}$Cho các phân giác của góc $A,B$ của $\Delta ABC$ cắt các cạnh $BC,CA$ tại $D$ và $E$.Giả sử rằng $AE+BD=AB$.Xác định $\angle C$

[The Collection]

$\boxed{\text{Bài toán 12}}$Cho các phân giác của góc $A,B$ của $\Delta ABC$ cắt các cạnh $BC,CA$ tại $D$ và $E$.Giả sử rằng $AE+BD=AB$.Xác định $\angle C$

 

Giải như sau:

 

 

Đặt $BC=a, CA=b, AB=c$.

 

Dùng các tính chất đường phân giác, kết hợp với giả thiết, ta có: \[\frac{AE}{AB}+\frac{BD}{AB}=1 \to \frac{b}{c+a}+\frac{a}{b+c}=1\] \[\to c^2=a^2+b^2-ab\]

 

Áp dụng định lý hàm số Cos suy ra: \[\cos C=\frac{1}{2} \to \angle C = 60^o\]

[Oral1020]

$\boxed{\text{Bài toán 13}}$ Cho $\Delta ABC$,$E$ và $F$ là những điểm nằm trên cạnh $BC$ và $CA$ sao cho $\dfrac{CE}{CB}+\dfrac{CF}{CA}=1$ và $\angle CEF=\angle CAB$.Giả sử $M$ là trung điểm của $EF$ và $G$ là giao điểm giữa $CM$ và $AB$.Chứng minh rằng các $\Delta FEG$ và $\Delta ABC$ đồng dạng

[Oral1020]

$\boxed{\text{Bài toán 14}}$ Cho $\Delta ABC$.$L$ là điểm $\text{Lemoine}$ và $F$ là điểm $\text{Fermat}$ (hay điểm $\text{Torricelli}$).$H$ là trực tâm và $O$ là tâm đường tròn ngoại tiếp.Gọi $1$ là đường thẳng $\text{Euler}$ và $1'$ là đối xứng của $1$ qua $AB$.$D$ là giao điểm của $1'$ với đường tròn ngoại tiếp,$E$ là giao điểm của $FL$ và $OD$.Gọi $G$ là giao điểm khác $H$ sao cho tam giác thủy túc (tam giác bàn chân) của $G$ đồng dạng với $\Delta \text{cevian}$ của $G$(đối với $\Delta ABC$).Chứng minh rằng hai góc $ACB,GCE$ hoặc chung hoặc những phân giác vuông góc với nhau.

[barcavodich]

$\boxed{\text{Bài toán 15}}$ Cho các điểm $ A_1,B_1,C_1 $ lần lượt nằm trên các cạnh $BC,CA,AC$ của tam giác $ABC$.Giả sử rằng $ AB_1-AC_1=CA_1-CB_1=BC_1-BA_1 $.Gọi $ I_A, I_B, I_C $ lần lượt là tâm nội tiếp các tam giác $ AB_1C_1,A_1BC_1,A_1B_1C $.CMR đường tròn ngoại tiếp tam giác $ I_AI_BI_C $ là tâm nội tiếp tam giác $ABC$

Bài viết đã được chỉnh sửa nội dung bởi NLT: 29-04-2013 - 13:14

[nguyenthehoan]

Ủng hộ topic $1$ bài nhá

Cho các điểm $ A_1,B_1,C_1 $ lần lượt nằm trên các cạnh $BC,CA,AC$ của tam giác $ABC$.Giả sử rằng $ AB_1-AC_1=CA_1-CB_1=BC_1-BA_1 $.Gọi $ I_A, I_B, I_C $ lần lượt là tâm nội tiếp các tam giác $ AB_1C_1,A_1BC_1,A_1B_1C $.CMR đường tròn ngoại tiếp tam giác $ I_AI_BI_C $ là tâm nội tiếp tam giác $ABC$

Theo bài ra $AB_{1}-AC_{1}=CA_{1}-CB_{1}=BC_{1}-BA_{1}$

 

$\Rightarrow BC_{1}+CB_{1}=BC$,...

 

Vẽ $A_{1}X\perp CI,A_{1}Y\perp BI$,Ta suy ra $A_{1}C=CX\Rightarrow AC_{1}=AX$  (vì $A_{1}C+AC_{1}=AC$)

 

Tương tự $AY=AB_{1}$.Gọi $D,E,F$ thứ tự là các tiếp điểm trên $BC,CA,AB$ của đường tròn nội tiếp tam giác $ABC$.

 

$CE=p-c,AE=p-a$,suy ra $B_{1}E=p-a-AB_{1},CE=p-c-CA_{1}$

 

Mà $a-c=CA_{1}-AB_{1}$ (vì $BY=BA_{1}$) nên $B_{1}E=EX\Rightarrow IA_{1}=IX=IB_{1}=IY$

 

Mặt khác Chứng minh tương tự trên ta có $C_{1}F=FY\Rightarrow IY=IC_{1}\Rightarrow IA_{1}=IB_{1}=IY=IC_{1}$

 

Hay $YB_{1}A_{1}C_{1}$ nội tiếp.$\Rightarrow \widehat{B_{1}A_{1}C_{1}}=\widehat{AYB_{1}}=\frac{\widehat{ABC}+\widehat{ACB}}{2}$   (***)

 

Tương tự ta cũng tính được các góc còn lại của $\Delta A_{1}B_{1}C_{1}$.

 

Vẽ $I_{a}M,I_{c}N\perp AC$,ta có $2ME=2(AE-AM)=AB+AC-BC-AB_{1}-AC_{1}+B_{1}C_{1}=B_{1}C_{1}$  (vì $BC_{1}+CB_{1}+BC$

 

Tương tự $2EN=A_{1}B_{1}$

.Vậy để cm $II_{a}=II_{c}$ ta phải cm $\frac{B_{1}C_{1}}{\cos \frac{BAC}{2}}=\frac{B_{1}A_{1}}{\cos \frac{\widehat{ACB}}{2}}$

 

Điều này hiển hiên đúng bằng cách áp dụng định lí $sin$ cho tam giác $A_{1}B_{1}C_{1}$ và áp dụng (***)

 

Vậy ta có $II_{a}=II_{c}$,tương tự ta suy ra $I$ là tâm ngoại tiếp $\Delta I_{a}I_{b}I_{c}$  (dpcm)

 

Hình vẽ http://upanh.com/vie...&id=9rvf5i5m9zm

[nguyenthehoan]

$\boxed{\text{Bài toán 13}}$ Cho $\Delta ABC$,$E$ và $F$ là những điểm nằm trên cạnh $BC$ và $CA$ sao cho $\dfrac{CE}{CB}+\dfrac{CF}{CA}=1$ và $\angle CEF=\angle CAB$.Giả sử $M$ là trung điểm của $EF$ và $G$ là giao điểm giữa $CM$ và $AB$.Chứng minh rằng các $\Delta FEG$ và $\Delta ABC$ đồng dạng

Gọi $X$ trên $AB$ sao cho $FX//CB$

 

Suy ra $\frac{CF}{CA}=\frac{BX}{BA}=1-\frac{AX}{AB}$

 

$\Rightarrow \frac{AX}{AB}=\frac{CE}{CB}\Rightarrow EX//AC$

 

Hay $CFXE$ là hình bình hành.

 

Vậy $X$ trùng $G$.Hay $CFGE$ là hình bình hành

 

Lại có $\widehat{CEF}=\widehat{CAB}$ nên từ đây dễ dàng suy ra 

 

$\Delta FEG\sim \Delta ABC$  (dpcm)

[NLT]

HIện tại bài toán 14 chưa có lời giải, cùng đến với bài toán mới:

 

$\boxed{\text{Bài toán 16}}$ Cho $\Delta ABC$ ngoại tiếp $(I)$, $(I)$ tiếp xúc $BC,CA,AB$ lần lượt tại $D,E,F$. Kẻ các đường kính $DD', EE', FF'$ của $(I)$. Gọi $M$ là trung điểm của $EF$. Gọi $A'$ là giao điểm của $D'M$ với $(I)$. Định nghĩa tương tự với $B', C'$. Chứng minh rằng: $A A', BB', CC'$ đồng quy.

[nguyenthehoan]

HIện tại bài toán 14 chưa có lời giải, cùng đến với bài toán mới:

 

$\boxed{\text{Bài toán 16}}$ Cho $\Delta ABC$ ngoại tiếp $(I)$, $(I)$ tiếp xúc $BC,CA,AB$ lần lượt tại $D,E,F$. Kẻ các đường kính $DD', EE', FF'$ của $(I)$. Gọi $M$ là trung điểm của $EF$. Gọi $A'$ là giao điểm của $D'M$ với $(I)$. Định nghĩa tương tự với $B', C'$. Chứng minh rằng: $A A', BB', CC'$ đồng quy.

Chào mừng Thịnh trở lại

 

Lời giải:Ta có $MA.MI=ME^{2}=ME.MF=MA'.MD'$ nên tứ giác $AD'IA'$ nội tiếp

 

Ta có $ID'=IA'$ nên $\widehat{D'AI}=\widehat{IAA'}$

 

Hay $AD'$ và $AA'$ là hai đường đẳng giác góc A của tam giác $ABC$.  (1)

 

Gọi $N$ là giao của $AD'$ là $BC$.Theo một bổ đề quen thuộc thì $N$ là tiếp điểm của đường tròn bàng tiếp góc $A$ lên $BC$

 

Bằng định lí Melelauyt ta có $AD'$,$BE'$ và $CF'$ đồng quy  (tại điểm Nagel của $\Delta ABC$) (2)

 

Từ (1) và (2) ta có ngay $AA',BB',CC'$ đồng quy tại điểm đẳng giác của điểm Nagel đối với tam giác $ABC$)

[NLT]

Chào mừng Thịnh trở lại

 

Lời giải:Ta có $MA.MI=ME^{2}=ME.MF=MA'.MD'$ nên tứ giác $AD'IA'$ nội tiếp

 

Ta có $ID'=IA'$ nên $\widehat{D'AI}=\widehat{IAA'}$

 

Hay $AD'$ và $AA'$ là hai đường đẳng giác góc A của tam giác $ABC$.  (1)

 

Gọi $N$ là giao của $AD'$ là $BC$.Theo một bổ đề quen thuộc thì $N$ là tiếp điểm của đường tròn bàng tiếp góc $A$ lên $BC$

 

Bằng định lí Melelauyt ta có $AD'$,$BE'$ và $CF'$ đồng quy  (tại điểm Nagel của $\Delta ABC$) (2)

 

Từ (1) và (2) ta có ngay $AA',BB',CC'$ đồng quy tại điểm đẳng giác của điểm Nagel đối với tam giác $ABC$)

 

Tớ có trở lại đâu, cách 2 nhé:

 

Gọi $A''$ là giao điểm của $A A'$ với $(I)$.

 

Theo bổ đề quen thuộc thì $ME$ là phân giác của $\angle A'MA''$.

 

Suy ra: $\angle A''MF=\angle D'ME \to A'', D'$ đối xứng nhau qua $AI$. 

 

Dẫn đến: $\angle BAA'=\angle CAD'$.

 

Dễ chứng minh $AD',BE',CF'$ đồng quy.

 

Dùng định lý Ceva sin ta có ngay $A A', BB', CC'$ đồng quy.