Chủ đề này có 6 trả lời

[uyenha]

Cho $\Delta ABC$ nội tiếp đường tròn $(I)$. Một đường tròn tiếp xúc với $AC,AB,(ABC)$ lần lượt ở $P,Q,R.AI$ cắt $(ABC)$ ở $T$. Chứng minh rằng $TR,PQ,BC$ đồng quy.

Bài viết đã được chỉnh sửa nội dung bởi NLT: 16-06-2013 - 16:19

[perfectstrong]

Đề này nhầm thì phải? Nếu gọi $(X)$ là đường tròn tiếp xúc trong $AC,AB,(ABC)$ thì $T$ phải là giao điểm của $AX$ và $(ABC)$ mới thỏa đề.

[The Collection]

Đề này nhầm thì phải? Nếu gọi $(X)$ là đường tròn tiếp xúc trong $AC,AB,(ABC)$ thì $T$ phải là giao điểm của $AX$ và $(ABC)$ mới thỏa đề.

 

Anh có thể chỉ cách dựng hình bài toán này không ạ? Dựng đường tròn $(X)$ như anh nói đấy ạ, em cảm ơn!

[perfectstrong]

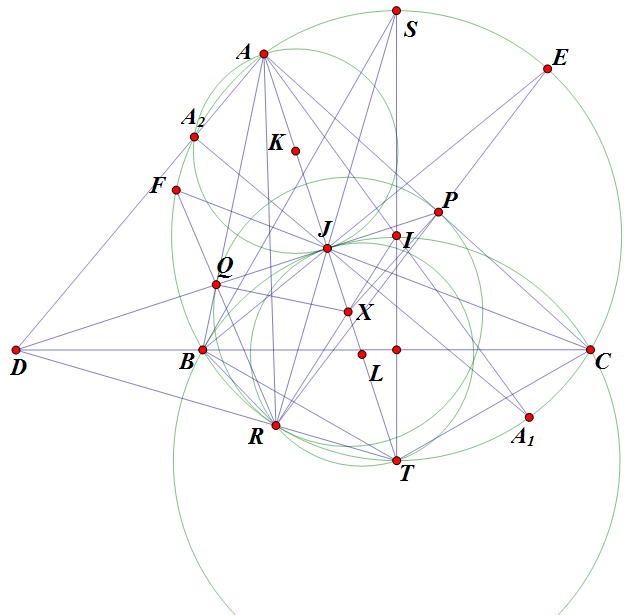
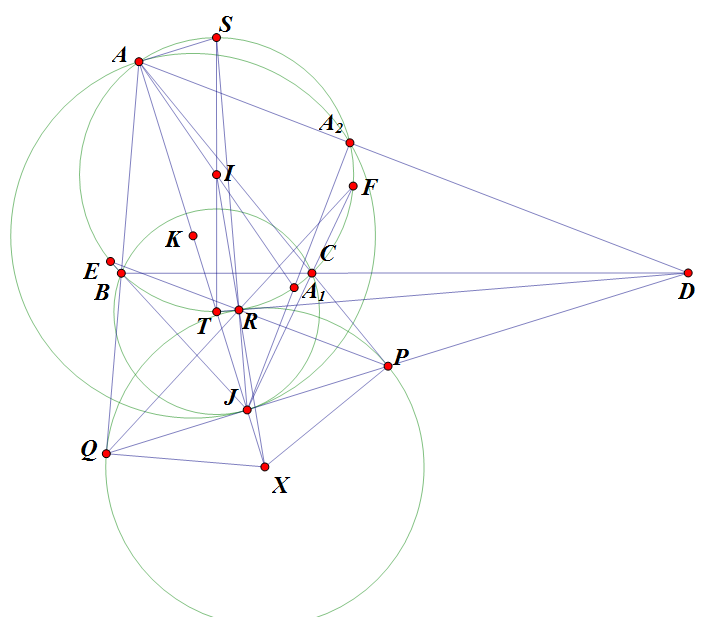
Bài toán thì anh chưa chứng minh được, nhưng cách dựng thì thế này:

Phân giác góc $ABC,ACB$ thứ tự cắt $(I)$ lần 2 tại $E,F$. Tiếp tuyến tại $E,F$ của $(I)$ cắt nhau ở $Z$. Vẽ $ZA$ cắt đường tròn $(I)$ lần thứ 2 tại $R$.

Phân giác góc $BAC$ cắt $IR$ tại $X$. Đường tròn $(X;XR)$ là đường tròn cần dựng.

[perfectstrong]

Đây là lời giải với TH $(X)$ nằm trong $(I)$.
Lời giải:
Nếu $\vartriangle ABC$ cân tại $A$ thì $RT \to$ tiếp tuyến $xy$ tại $T$ của $(I)$. Dễ thấy khi đó $QP,BC,xy$ đôi một song song.
Xét TH $\vartriangle ABC$ không cân tại $A$.
Gọi $(X)$ là đường tròn đi qua $P,Q,R$.Vẽ $RQ,RP$ thứ tự cắt $(I)$ lần thứ 2 tại $F,E$.
Nhận xét 1: $E,F$ thứ tự là trung điểm cung $AC,AB$.
==================================================
$CF,BE$ cắt nhau tại $J$. Từ nhận xét 1, suy ra $BE,CF$ là phân giác $\angle ABC,\angle ACB$ tương ứng. Do đó, $J$ là tâm đường tròn nội tiếp $\vartriangle ABC$.
Nhận xét 2: $PQ$ đi qua $J$ (định lý Lyness)
Chứng minh nhận xét 2:
Áp dụng định lý Pascal cho 6 điểm $(R,F,C,A,B,E)$ có $RF \cap AB=Q; FC \cap BE=J; CA \cap RE=P$, ta có ngay $P,I,Q$ thẳng hàng.
==================================================
Nhận xét 3: $T$ là tâm đường tròn ngoại tiếp $\vartriangle JBC$. Gọi đó là đường tròn $(T)$.
==================================================
Vẽ đường kính $AA_1$ của $(I)$. $JA_1$ cắt $(I)$ lần 2 tại $A_2 \Rightarrow \angle JA_2A=90^o$.
Gọi $(K)$ là đương tròn ngoại tiếp $\vartriangle JA_2A \Rightarrow K$ là trung điểm $JA$ nên $K,J,T$ thẳng hàng.
Do đó, $(K)$ tiếp xúc với $(T)$. Gọi $Jx$ là trục đẳng phương của $(K),(T)$.
Mà ta cũng có $A_2A;BC$ thứ tự là trục đẳng phương của cặp đường tròn $((K);(I));((T);(I))$ nên $BC,A_2A,Jx$ đồng quy
($BC,A_2A;Jx$ không thể đôi một song song vì $AB \ne AC \Rightarrow I \not \in AT \Rightarrow I,K,T$ không thẳng hàng).
Vẽ $BC$ cắt $A_2A$ tại $D \quad (i) \Rightarrow DJ \perp AT$
Từ nhận xét 2, dễ thấy rằng $PQ \perp AT$ tại $J \Rightarrow PQ$ đi qua $D$. (ii)

===================================================
Ta chỉ cần chứng minh $RT$ đi qua $D$ (iii)
Nhận xét 4: $\angle JRT=90^o$
Vẽ đường kính $TS$ của $(I)$. Ta sẽ chứng minh $R,J,S$ thẳng hàng. Gọi $R$ là bán kính của $(I)$.
Ta có:\[ \begin{array}{l} XQ = XR = AQ\tan \frac{{BAC}}{2} \\ JX = JQ\tan JQX = \left( {AQ\sin \frac{{BAC}}{2}} \right)\tan \frac{{ABC}}{2} \\ TJ = TB = 2R\sin \frac{{BAC}}{2} \\ \Rightarrow \frac{{\overline {RX} }}{{\overline {RI} }}.\frac{{\overline {SI} }}{{\overline {ST} }}.\frac{{\overline {JT} }}{{\overline {JX} }} = \frac{{RX}}{{RI}}.\frac{{SI}}{{ST}}.\frac{{JT}}{{JX}} = \frac{{AQ\tan \frac{{BAC}}{2}}}{R}.\frac{1}{2}.\frac{{2R\sin \frac{{BAC}}{2}}}{{\left( {AQ\sin \frac{{BAC}}{2}} \right)\tan \frac{{ABC}}{2}}} = 1 \\ \end{array} \]
Theo định lý Menelaus đảo cho $\vartriangle TXI$, ta có $R,J,S$ thẳng hàng. Suy ra $\angle JRT=\angle SRT=90^o$.

Gọi $(L)$ là đường tròn ngoại tiếp $\vartriangle JRT \Rightarrow L$ là trung điểm $JT$, nên $K,J,L$ thẳng hàng.
Do đó $(K)$ tiếp xúc $(L)$. Mà $JD$ là tiếp tuyến của $(K)$ nên $JD$ cũng là trục đẳng phương của $(K),(L)$.
Mặt khác, $A_2A, RT$ thứ tự là trục đẳng phương của cặp đường tròn $((K);(I));((L);(I))$ và $A_2A;JD$ cắt nhau tại $D$.
Suy ra $RT$ qua D. (iii) được chứng minh.
===================================================
Từ (i),(ii),(iii), ta có đpcm.


Điều đặc biệt: Kể cả khi $(X)$ nằm ngoài $(I)$, bài toán vẫn đúng nếu $T$ là giao điểm thứ 2 của $AX$ và $(I)$.
Chứng minh TH2:
Khi $(X)$ nằm ngoài $(I)$, chứng minh trên vẫn không thay đổi gì nhiều. Chỉ thay đổi 3 điều nhỏ, không ảnh hưởng đến cả bài toán:
1. $E$ là trung điểm cung $ABC$ và $F$ là trung điểm cung $ACB$.
2. $J$ là tâm đường tròn bàng tiếp $\angle BAC$ của $\vartriangle BAC$
3. \[
\frac{{\overline {RX} }}{{\overline {RI} }}.\frac{{\overline {SI} }}{{\overline {ST} }}.\frac{{\overline {JT} }}{{\overline {JX} }} = \left( { - \frac{{RX}}{{RI}}} \right).\frac{{SI}}{{ST}}.\left( { - \frac{{JT}}{{JX}}} \right) = \frac{{RX}}{{RI}}.\frac{{SI}}{{ST}}.\frac{{JT}}{{JX}}
\]

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 24-04-2013 - 08:15

[The Collection]

 

 

Anh Hân đã làm quá dài dòng thì phải ^^, giải như sau: 

 

 

Gọi $P$ là giao điểm của $BC$ và $RT$, $X,Y$ lần lượt là giao điểm của $RE,RF$ với $(ABC)$.

 

Ta có: $X,Y$ lần lượt là điểm chính giữa của cung $AB, AC$, và $I$ thuộc $EF$ (trong chứng minh của anh Hân đã nhắc tới $2$ điều này), rõ ràng $BY,CX$ cắt nhau tại $I$

 

Áp dụng định lý Pascal cho lục giác nôi tiếp $RTABCX$, ta được $I,E,P$ thẳng hàng, tức là $P \in EF$, và đó là điều phải chứng minh. 

 

...Secret...

 

@perfectstrong: Lời giải hay tuyệt đấy tranminhbao2607 Anh cũng không nghĩ tới điều này. Nhưng mỗi lời giải đều có cái hay riêng

 

@tranminhbao2607: Em chỉ tự dưng nhận ra thôi ạ ^^  Vâng, lời giải của anh cực kỳ bá đạo ^^ và rất tuyệt

Bài viết đã được chỉnh sửa nội dung bởi tranminhbao2607: 30-04-2013 - 08:54

[thukilop]

Gọi D là giao điểm PT và BC. Ta chứng minh D,Q,P thẳng hàng bằng menelaus $<=>\frac{\overline{DC}}{\overline{DB}}.\frac{\overline{QB}}{\overline{QA}}.\frac{\overline{PA}}{\overline{PC}}=1 <=> \frac{\overline{DC}}{\overline{DB}}=\frac{\overline{PC}}{\overline{QB}}$ 

Mà điều này dễ thấy: $\frac{\overline{PC}}{\overline{QB}}=\frac{\frac{sin(DP,DC)}{sin(PD,PC)}.\overline{DC}}{\frac{sin(DQ,DB)}{sin(QD,QB)}.\overline{DB}}$ mà $\angle APQ=\angle AQP$ => dpcm 

------------------------------

Còn 1 cách dựng đtròn (X) nữa: Dựng tâm đường tròn nội tiếp ABC, gọi là O. Kẻ đường thẳng qua O vuông góc AO cắt AB tại D. Kẻ đường thẳng qua D vuông góc AB cắt AO tại X. Ta được đt (X,XD)

Bài viết đã được chỉnh sửa nội dung bởi thukilop: 03-05-2014 - 08:08