NLT

Lại một bài nữa về đường tròn nội tiếp

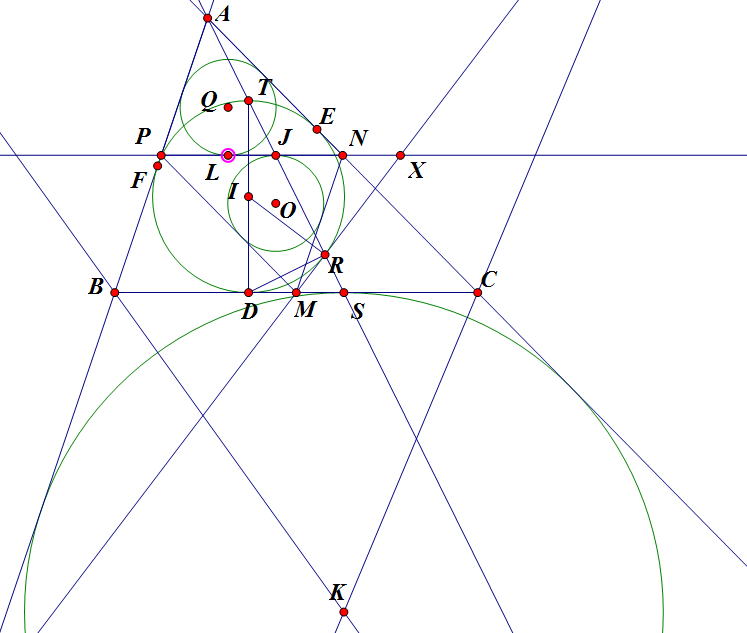
$\boxed{\text{Bài toán 22}}$ Cho tam giác $ABC$ nội tiếp đường tròn $(I)$, gọi $O_A, O_B,O_C$ lần lượt là giao điểm của các đường phân giác góc $\angle A, \angle B, \angle C$ với $(I)$. Gọi $(O_A)$ là đường tròn tâm $O_A$ và tiếp xúc với $AB,AC$. Định nghĩa tương tự với $(O_B),(O_C)$. Gọi $t_A$ là tiếp tuyến chung ngoài của $(O_B)$ và $(O_C)$, định nghĩa tương tự với $t_B, t_C$. Chứng minh rằng $t_A, t_B,t_C$ đồng quy.

[49192]

Và một vấn đề quen thuộc nhưng hoàn toàn không hề cũ

$\boxed{\text{Bài toán 23}}$ Cho $\omega_1$ và $\omega_2$ với các bán kính $r_1,r_2$ thỏa $r_2>r_1$ tiếp xúc ngoài với nhau. $t_1$ tiếp xúc với $\omega_1, \omega_2$ lần lượt tại $A,D$. Kẻ $t_2 // t_1$ và tiếp xúc với $\omega_1$, nó cắt $\omega_2$ lần lượt tại $E,F$. Kẽ $t_3$ đi qua $D$  cắt $t_2, \omega_2$ lần lượt tại $B,C$ (khác $E,F$ tương ứng). Chứng minh rằng đường tròn ngoại tiếp của $\Delta ABC$ tiếp xúc với $t_1$.

[53277]

^^ Bài 16 tớ cũng giải như cậu, thế là bài 17 ta đã có 3 cách giải

Tiếp tục nào:

$\boxed{\text{Bài toán 19}}$ Cho $\Delta ABC$. $A'$ là trung điểm của $BC$. $T_a$ là tiếp điểm của đường tròn nội tiếp tam giác với $BC$. Vẽ đường tròn tâm $A'$ đi qua $T_a$. Định nghĩa tương tự với $(B'),(C')$. Chứng minh rằng nếu $(A')$ tiếp xúc với đường tròn ngoại tiếp $\Delta ABC$ thì $(B')$ hoặc $(C')$ cũng tiếp xúc với đường tròn ngoại tiếp $\Delta ABC$. 

Xin gởi tiếp mẫu cho HH, tôi dùng trực tiếp các hình đã đưa lên diễn đàn

HHMathLinks.rar

Vì em chưa có kinh nghiệm làm những kiểu như thế này, em xin nhờ thầy Hùng biên soạn giúp phần hình học được không ạ, em sẽ bổ sung các hình. Em chưa học $\LaTeX$ ạ, em sẽ cố gắng hoàn thành Topic 100 bài trong thời gian sớm nhất, em xin cảm ơn thầy

Chào mừng Thịnh trở lại

 

Lời giải:Ta có $MA.MI=ME^{2}=ME.MF=MA'.MD'$ nên tứ giác $AD'IA'$ nội tiếp

 

Ta có $ID'=IA'$ nên $\widehat{D'AI}=\widehat{IAA'}$

 

Hay $AD'$ và $AA'$ là hai đường đẳng giác góc A của tam giác $ABC$.  (1)

 

Gọi $N$ là giao của $AD'$ là $BC$.Theo một bổ đề quen thuộc thì $N$ là tiếp điểm của đường tròn bàng tiếp góc $A$ lên $BC$

 

Bằng định lí Melelauyt ta có $AD'$,$BE'$ và $CF'$ đồng quy  (tại điểm Nagel của $\Delta ABC$) (2)

 

Từ (1) và (2) ta có ngay $AA',BB',CC'$ đồng quy tại điểm đẳng giác của điểm Nagel đối với tam giác $ABC$)

Tớ có trở lại đâu, cách 2 nhé:

Gọi $A''$ là giao điểm của $A A'$ với $(I)$.

Theo bổ đề quen thuộc thì $ME$ là phân giác của $\angle A'MA''$.

Suy ra: $\angle A''MF=\angle D'ME \to A'', D'$ đối xứng nhau qua $AI$. 

Dẫn đến: $\angle BAA'=\angle CAD'$.

Dễ chứng minh $AD',BE',CF'$ đồng quy.

Dùng định lý Ceva sin ta có ngay $A A', BB', CC'$ đồng quy.

HIện tại bài toán 14 chưa có lời giải, cùng đến với bài toán mới:

$\boxed{\text{Bài toán 16}}$ Cho $\Delta ABC$ ngoại tiếp $(I)$, $(I)$ tiếp xúc $BC,CA,AB$ lần lượt tại $D,E,F$. Kẻ các đường kính $DD', EE', FF'$ của $(I)$. Gọi $M$ là trung điểm của $EF$. Gọi $A'$ là giao điểm của $D'M$ với $(I)$. Định nghĩa tương tự với $B', C'$. Chứng minh rằng: $A A', BB', CC'$ đồng quy.

Một mở rộng khác, điều này khá thú vị

Cho $\Delta ABC$, $(I)$ nội tiếp $\Delta ABC$, $E,F$ là các tiếp điểm như hình vẽ. $2$ điểm $M,N$ bất kì thuộc đoạn $AD. L,K,U,T$ là các điểm như hình vẽ. Chứng minh: $LT,KU,AD$ đồng quy.

Lưu ý: Các bạn khi post bài phải nhắn tin cho mình link bài toán đó tại Mathlinks.ro, vì có nhiều bạn không đọc Tiêu đề, nội dung của Topic này mà vào post bài không nằm trên Mathlinks.ro. Cảm ơn !

Mở rộng bài toán 10:

Không phải điểm $I$ là tâm đường tròn nội tiếp nữa, cho $I$ chạy bất kì trên $AD$, Kẽ $IM,IN,IP$ lần lượt vuông góc $AB,BC,CA$, khi đó $AK,MP,IM$ đồng quy, với $K$ là trung điểm của $BC$. Chứng minh hoàn toàn tương tự. 

Tìm tổng 3 số nguyên dương khác nhau biết tổng nghịch đảo của chúng bằng 1

Ta có: $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$

Không mất tính tổng quát giả sử $a\ge b\ge c$.

Nếu $c \ge 4 \to \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \le \frac{3}{4}<1$.

Nên: $c = {1,2,3}$. Thử từng giá trị, tiếp tục dùng phương pháp như trên tìm được $a,b$.

Bài này là 1 bài rất cơ bản về phương pháp xuống thang (sắp xếp thứ tự), bạn có thể tìm thấy nhiều tài liệu (các sách viết về phương trình nghiệm nguyên đều có bài tương tự thế này).

$\boxed{\text{Bài toán 10}}$ Cho $\Delta ABC$ có đường tròn tâm $(I)$ nội tiếp, tiếp xúc với các cạnh $BC,CA,AC$ lần lượt tại $D,E,F$. Trung tuyến $AM$ cắt $EF$ tại $J$.Chứng minh : $D,I,J$ thẳng hàng.

Bài toán này không khó, bạn có thể nhắn tin cho mình link của nó trên Mathlinks.ro không?

Giải như sau:

Gọi $J'$ là giao điểm của $DI$ và $EF$, qua $I$ kẻ đưởng thẳng song song với $BC$ cắt $AB,AC$ lần lượt tại $P,N$. Ta chứng minh $J \equiv J'$ hay cần chứng minh $J' \in AM$. 

Như vậy đưa đến việc chứng minh: $J'$ là trung điểm của $PN$, từ đó theo định lý Thales có ngay $J' \in AM$.

Để ý rằng $FJ'E$ là đường thẳng Simson của $\Delta APN \to I, A,P,Q$ đồng viên.

Mà $AI$ là phân giác của góc $\angle PAN \to IP=IN \to J'$ là trung điểm của $PN$, và dẫn đến điều phải chứng minh!

Cho tứ giác lồi ABCD nội tiếp đường tròn tâm O , AD giao BC tại M, AB giao CD tại N, AC giao BD tại I. Chứng minh O là trực tâm của tam giác MIN.

:| Đây chỉ là 1 tính chất quen thuộc. Chứng minh bằng cách gọi $H$ là giao điểm thứ $2$ của $(ADI)$ và $(BIC)$, khi đó $MA.MD=MB.MC \to M$ thuộc trục đẳng phương của $(AIHD),(BIHC)$. Không khó để chứng minh các tứ giác $DOHC, AOHB$ nội tiếp, từ đó: \[\angle OHM = \angle DHM-\angle DHO=\angle ADC+\angle ACD - \angle OCD = \angle ADC + \angle OCA = 1 V \to MI \perp ON\]. Tương tự $NI \perp OM \to Q.E.D$.

Ngắm tạm cái bìa này cho đỡ "vật" nhé!

BiaML.png

Ôi thầy ơi, đẹp quá ^^ À nhưng mà có cùng màu với chuyên đề ĐTTH không ta

Nhìn cái bìa đẹp quá, ráng làm thôi Mọi người cứ lo các phần khác ạ, em với Hoàn sẽ chăm cày phần Hình học, còn việc đưa vào TEX phải nhờ ai đó rồi . Tất cả các bài giải đã có trên diễn đàn, em với Hoàn sẽ cố gắng kiếm thêm, mới được chục bài à, buồn quá Gía như anh Hân tham gia thì tốt quá, bên hình mà ảnh im hơi lặng tiếng quá

Không biết có phải là "Kết nối 96 để cùng học tập" không nữa =.= 

Cho $\Delta ABC$ nội tiếp đường tròn $(O)$, đường tròn $(I)$ nội tiếp tam giác, $(I)$ tiếp xúc với $BC,CA,AB$ lần lượt tại $M,N,P$. Gọi $H$ là trực tâm $\Delta MNP$. Chứng minh rằng $O,I,H$ thẳng hàng.

Ủng hộ topic của Thịnh một bài.

 

$\boxed{\text{Bài toán 9}}$ Cho $\Delta ABC$ ngoại tiếp đường tròn $(I)$. Gọi $M, N, P$ thứ tự là trung điểm của $BC, CA, AB$.

Qua M vẽ tiếp tuyến với $(I)$, cắt $NP$ tại $X$. Các điểm $Y,Z$ xác định tương tự trên $PM$, $MN$.

Chứng minh rằng $X,Y,Z$ thẳng hàng.

Nhờ gợi ý của Hoàn, xin trình bày lời giải vắn tắt:

Gọi $S$ là giao điểm của $AT$ và $BC$ với $T$ là điểm thuộc $(I)$ sao cho $DI$ là đường kính của $(I)$.

Dựng đường tròn bàng tiếp góc $\angle A$ của $\Delta ABC$, khi đó, dễ thấy, qua phép vị tự tâm $A$ tỉ số $\frac{AI}{AK}$ thì $ (I) \to (K); T \to S$

Nên $S$ là tiếp điểm của tiếp tuyến tại $C$ của $(K)$. Không khó để suy ra $CS=BD (=p-a)$.

Do $M$ là trung điểm $BC$ nên $M$ là trung điểm của $DS$, giả sử $AS$ cắt $(I)$ tại điểm thứ $2$ là $R$, khi đó $\Delta DRS$ vuông tại $R$, có $M$ là trung điểm nên $MD=MR$, lại có $MD$ là tiếp tuyến tại $D$ của $(I)$, nên $MR$ là tiếp tuyến của $(I)$, do đó $X$ là giao điểm của $MR$ và $NP$.

Dựng $(Q)$ nội tiếp tam giác $\Delta APN$, $L$ là tiếp điểm của $PN$ với $(Q)$, rõ ràng qua phép vị tự tâm $A$ tỉ số $\frac{AI}{AQ}$, biến $(I) \to (Q)$, từ đó cũng biến $(K) \to (O); S \to J$, do đó $J$ là tiếp điểm của $PN$ với đường tròn $(O)$.

Để ý rằng: $\Delta MRS \sim \Delta XRJ \to XR=XJ \to X$ nằm trên trục đẳng phương của $(I)$ và đường tròn nội tiếp $\Delta MNP$, tương tự ta cũng có $Y,Z$ nằm trên đường đó, cuối cùng có $Q.E.D$.

P/s: To nguyenthehoan: Bài này quá hay ^^, tks cậu đã gợi ý Vấn đề: Liệu có thể thay đổi tỉ số $M,N,P$ trên $BC,CA,AB$, không phải trung điểm nữa?