DarkBlood

Cho $a,b,c$ là các số thực dương thỏa mãn $$7(a^2+b^2+c^2)=11(ab+bc+ca)$$

Chứng minh rằng $$\dfrac{51}{28} \leq \sum \dfrac{a}{b+c} \leq 2$$

Câu 5 : Cho $a,b,c,d>0$ có tổng bằng $4$. Tìm giá trị nhỏ nhất :

$$P=\dfrac{(a^2+1)(b^2+1)(c^2+1)(d^2+1)}{abc+bcd+cda+dab}$$

Ta có: $(a^2+1)(b^2+1)\geq(a+b)^2$

Tương tự suy ra $(a^2+1)(b^2+1)(c^2+1)(d^2+1)\geq(a+b)(b+c)(c+d)(d+a)$

Ta chứng minh $(a+b)(b+c)(c+d)(d+a)\geq(a+b+c+d)(abc+bcd+cda+dab) \Leftrightarrow (ac-bd)^2$ $($Đúng$)$

Do đó $(a^2+1)(b^2+1)(c^2+1)(d^2+1)\geq 4(abc+bcd+cda+dab)$ 

$\Rightarrow P\geq 4$

Đẳng thức xảy ra khi $a=b=c=d=1$

Giải phương trình $$\sqrt{\dfrac{3}{1-k}}+\dfrac{3}{\sqrt{2(1-2k)}}+\dfrac{2}{\sqrt{1-3k}}=20$$

Mời mọi ngườiimage.jpg

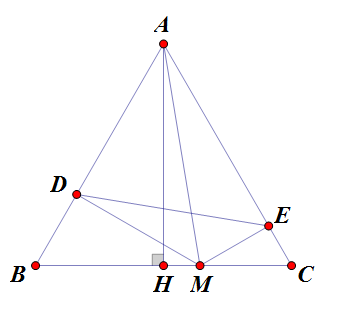
Câu 3:

Ta có $DM+EM=(BM+CM).\textrm{sin}\ 60^{\circ}=BC.\textrm{sin}\ 60^{\circ}=\textrm{const}$

Do đó chu vi tam giác $MDE$ nhỏ nhất $\Leftrightarrow$ $DE$ nhỏ nhất.

Tam giác $ADE$ nội tiếp đường tròn đường kính $AM$ nên $DE=AM.\textrm{sin}\widehat{\textrm{BAC}}=AM.\textrm{sin}\ 60^{\circ}$

Vì $\textrm{sin}\ 60^{\circ}$ không đổi nên $DE$ nhỏ nhất $\Leftrightarrow$ $AM$ nhỏ nhất $\Leftrightarrow$ $M\equiv H$ $(H$ là chân đường vuông góc hạ từ $A$ xuống $BC)$

Vậy khi $M$ là chân đường vuông góc hạ từ $A$ xuống $BC$ thì chu vi tam giác $MDE$ nhỏ nhất.

Câu 5: 

a) $AO$ cắt $(O)$ tại $E,$ $EH$ cắt $(O)$ tại $K',$ $AK'$ cắt $EB$ tại $D.$ 

Dễ thấy $H$ là trực tâm tam giác $AED$ nên $DH\perp AO \Rightarrow DH\parallel AM$

Ta có $\widehat{BDH}=\widehat{EAH}=\widehat{HMB}$ nên tứ giác $HMDB$ nội tiếp

Suy ra $\widehat{HMD}=180^{\circ}-\widehat{HBD}=90^{\circ}$

$\Rightarrow HM\perp MD \Rightarrow DM\parallel AH$

Do đó tứ giác $AHDM$ là hình bình hành

$\Rightarrow$ $AD$ đi qua trung điểm $I$ của $HM$

$\Rightarrow$ $K'$ là giao điểm của $AI$ với $(O)$

$\Rightarrow$ $K'\equiv K$

$\Rightarrow$ $HK\perp AI$

b) Ta có

$\widehat{IAM}=\widehat{ABK}$ $(AM$ là tiếp tuyến$)$

$\widehat{AMI}=\widehat{OBA}$

Nên $\widehat{IAM}+\widehat{AMI}=\widehat{ABK}+\widehat{OBA}$

$\Leftrightarrow \widehat{AIH}=\widehat{OBK}$

Mặt khác

$\widehat{AIH}+\widehat{KHI}=90^{\circ}$

$\widehat{OBK}+\widehat{KBM}=90^{\circ}$

Nên $\widehat{KHI}=\widehat{KBM}$

$\Rightarrow$ Tứ giác $HKMB$ nội tiếp 

$\Rightarrow$ $\widehat{BKM}=\widehat{BHM}=90^{\circ}$

Cho hai phương trình $x^2+bx+c=0$ $(1)$ và $x^2-b^2x+bc=0$ $(2).$ BIết phương trình $(1)$ có hai nghiệm $x_1, x_2$ và phương trình $(2)$ có hai nghiệm $x_3, x_4$ thỏa mãn điều kiện $x_3-x_1=x_4-x_2=1.$ Xác định $b$ và $c.$

Với $a,b,c \geq0$, chứng minh rằng:

$a+b+c\geq 3\sqrt[3]{abc}$

p/s: Chứng minh theo BĐT Cô-si cho 2 số.

BĐT tưởng đương $a+b+c+\sqrt[3]{abc}\geq 4\sqrt[3]{abc}$

Áp dụng BĐT Cô si 2 số 

$a+b\geq 2\sqrt{ab}$

$c+\sqrt[3]{abc}\geq 2\sqrt{c\sqrt[3]{abc}}$

$\sqrt{ab}+\sqrt{c\sqrt[3]{abc}}\geq 2\sqrt[4]{abc\sqrt[3]{abc}}=2\sqrt[3]{abc}$

Từ đó có điều phải chứng minh.

Câu III:
Cho tam giác $ABC$ nội tiếp $(O)$ và điểm $P$ nằm trong tam giác sao cho $BP=PC$. $D$ là điểm nằm trên $BC$ ($D$ nằm giữa $B$ và $C$) sao cho $P$ nằm trong đường tròn ngoại tiếp tam giác $DAB$ và đường tròn ngoại tiếp tam giác $DAC$. Đường thẳng $PB$ cắt đường tròn ngoại tiếp tam giác $DAB$ tại $E$ khác $B$. Đường thẳng $PC$ cắt đường tròn ngoại tiếp tam giác $DAC$ tại $F$ khác$C$.
1) CMR 4 điểm $A,E,P,F$ thuộc 1 đường tròn.
2) Giả sử đường thẳng $AD$ cắt $(O)$ tại $Q$ khác $A$, đường thẳng $AF$ cắt đường thẳng$CQ$ tại $L$. CMR $\triangle ABE$ đồng dạng với $\triangle CLF$.
3) Gọi $K$ là giao điểm của đường thẳng $AE$ và đường thẳng $QB$. CMR $\widehat{QKL}+\widehat{PAB}=\widehat{QLK}+\widehat{PAC}$.

Câu 3

Cho mượn cái hình nha Hiếu

Ta có $\bigtriangleup BAE \sim \bigtriangleup LCF \Rightarrow LF.AE=BE.CF$

Tương tự $KE.AF=BE.CF$ suy ra $KE.AF=LF.AE \Leftrightarrow \dfrac{LF}{AF}=\dfrac{KE}{AE}$

Suy ra $EF \parallel LK \Leftrightarrow \widehat{AEF}=\widehat{AKL}$

$\Leftrightarrow \widehat{APF}=\widehat{AKL}$

$\Leftrightarrow \widehat{PAC}+\widehat{PCA}=\widehat{EKB}+\widehat{QKL}$

Mà $\widehat{PCA}=\widehat{EKB}$ $($vì $\bigtriangleup CAF \sim \bigtriangleup KBE)$

Nên $\widehat{PAC}=\widehat{QKL}$

Tương tự $\widehat{PAB}=\widehat{QLK}$

Suy ra điều phải chứng minh.

Câu I:
1) Giả sử $x,y$ là những số thực dương phân biệt thoả mãn:
$\frac{y}{x+y}+\frac{2y^{2}}{x^{2}+y^{2}}+\frac{4y^{4}}{x^{4}+y^{4}}+\frac{8y^{8}}{x^{8}-y^{8}}= 4$
CMR $4x=5y$
Câu II:
1) Cho $x,y$ là những số nguyên lớn hơn 1 sao cho $4x^{2}y^{2}-7x+7y$ là số chính phương. CMR $x=y$
2) Giả sử $x,y$ là những số thực không âm thoả mãn $x^{3}+y^{3}+xy=x^{2}+y^{2}$. Tìm max và min của biểu thức
$P=\frac{1+\sqrt{x}}{2+\sqrt{y}}+\frac{2+\sqrt{x}}{1+\sqrt{y}}$

Câu I Quy đồng  Có 3 mẫu đầu nhân nhau nhân với $x-y$ thành mẫu thứ 4

Câu II

1) Đặt $4x^2y^2-7x+7y=A$

Xét $x>y\geq 2$

Ta chứng minh $(2xy-1)^2<A<(2xy+1)^2$

$\Leftrightarrow -4xy+1<-7x+7y<4xy+1$

Vì $x>y$ nên $-7x+7y<0<4xy+1$

Ta có $-4xy+1\leq -8x+1<-7x+7y$ $($Do $x,y\geq 2)$

Do đó $A=4x^2y^2 \Rightarrow x=y$ $($Vô lý$)$

Xét $y>x\geq 2$ 

Tương tự suy ra $x=y$ $($Vô lý$)$

Vậy $x=y.$

2) Từ giả thiết suy ra $x=y=0$ hoặc $x+y=1$

Xét $x=y=0$ ta có $P=\dfrac{3}{2}$

Xét $x+y=1$ suy ra $x,y\leq 1$

Ta có

$\frac{4}{3}=\dfrac{1+0}{2+1}+\dfrac{2+0}{1+1}\leq \dfrac{1+\sqrt{x}}{2+\sqrt{y}}+\dfrac{2+\sqrt{x}}{1+\sqrt{y}}\leq \dfrac{1+1}{2+0}+\dfrac{2+1}{1+0}=4$

Vậy $\textrm{min} P=\dfrac{4}{3}$ khi $x=0, y=1.$

$\textrm{max} P=4$ khi $x=1, y=0.$

ĐẠI HỌC QUỐC GIA TP HCM
TRƯỜNG PHỔ THÔNG NĂNG KHIẾU

HỘI ĐỒNG TUYỂN SINH

_________________________
ĐỀ THI TUYỂN SINH LỚP 10

Năm học 2014 - 2015
Môn thi: Toán (chuyên)
Thời gian làm bài: 150 phút, không kể thời gian phát đề

Câu I. Cho phương trình $(m^2+5)x^2-2mx-6m=0\,(1)$ với $m$ là tham số .
a) Tìm $m$ sao cho phương trình $(1)$ có hai nghiệm phân biệt. Chứng minh rằng khi đó tổng của hai nghiệm không thể là số nguyên.
b) Tìm $m$ sao cho phương trình $(1)$ có hai nghiệm $x_1,x_2$ thỏa mãn điều kiện
$$\left(x_1x_2-\sqrt{x_1+x_2}\right)^4=16$$
Câu II. 1) Giải hệ phương trình $\left\{\begin{matrix}
2\left(1+x\sqrt{y}\right)^2=9y\sqrt{x}\\
2\left(1+y\sqrt{x}\right)^2=9x\sqrt{y}
\end{matrix}\right.$
2) Cho tam giác ABC vuông tại A với các đường phân giác trong BM và CN. Chứng minh bất đẳng thức $\dfrac{(MC+MA)(NB+NA)}{MA.NA} \geq 3+2\sqrt{2}$
Câu III. Cho các số nguyên dương $a,b,c$ sao cho $\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{c}$
a) Chứng minh rằng $a+b$ không thể là số nguyên tố.
b) Chứng minh rằng nếu $c>1$ thì $a+c$ và $b+c$ không thể đồng thời là số nguyên tố.
Câu IV. Cho điểm C thay đổi trên nửa đường tròn đường kính $AB=2R\, (C \neq A, C \neq B)$. Gọi H là hình chiếu vuông góc của C lên AB; I và J lần lượt là tâm đường tròn nội tiếp các tam giác ACH và BCH. Các đường thẳng Ci, CJ cắt AB lần lượt tại M, N.
a) Chứng minh rằng AN=AC, BM=BC.
b) Chứng minh 4 điểm M, N, J, I cùng nằm trên một đường tròn và các đường thẳng MJ, NI, CH đồng quy.
c) Tìm giá trị lớn nhất của MN và giá trị lớn nhất của diện tích tam giác CMN theo R.
Câu V. Cho 5 số tự nhiên phân biệt sao cho tổng của ba số bất kỳ trong chúng lớn hơn tổng của hai số còn lại.
a) Chứng minh rằng tất cả 5 số đã cho đều không nhỏ hơn 5.
b) Tìm tất cả các bộ gồm 5 số thỏa mãn đề bài mà tổng của chúng nhỏ hơn 40.

......................Hết......................
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:...................... Số báo danh:......................

Cho phương trình $ax^{2}+bx+c=0(a\neq 0)$ có 2 nghiệm $x_{1},x_{2}$ thỏa mãn điều kiện $0\leq x_{1}\leq x_{2}\leq 2$ Tìm Max $Q=\frac{2a^{2}-3ab+b^{2}}{2a^{2}-ab+ac}$

ĐK: $b^2\geq 4ac$

Theo hệ thức viet, ta có: 

$x_1+x_2=\dfrac{-b}{a}$

$x_1x_2=\dfrac{c}{a}$

Từ gt, suy ra $x_1^2\leq x_1x_2$ và $x_2^2\leq 4$

Ta có:

$\textrm{Q}=\dfrac{2a^2-3ab+b^2}{2a^2-ab+ac}=\dfrac{2-3\dfrac{b}{a}+\dfrac{b^2}{a^2}}{2-\dfrac{b}{a}+\dfrac{c}{a}}$

$=\dfrac{2+3(x_1+x_2)+(x_1+x_2)^2}{2+x_1+x_2+x_1x_2}$

$=\dfrac{2+3x_1+3x_2+x_1^2+2x_1x_2+x_2^2}{2+x_1+x_2+x_1x_2}$

$\leq \dfrac{2+3x_1+3x_2+2x_1x_2+x_1x_2+4}{2+x_1+x_2+x_1x_2}$

$=3$

Vậy $\textrm{Max}\ \textrm{Q}=3.$

Dấu bằng khi $4a=-b=c$ hoặc $2a=-b, c=0.$

Cho $a,b,c,d$ dương thỏa mãn: $a+b+c+d=1$. CMR: $\frac{2}{(a+b)(c+d)}\leqslant \frac{1}{\sqrt{ab}}+\frac{1}{\sqrt{cd}}$

Ta có $\dfrac{1}{\sqrt{ab}}+\dfrac{1}{\sqrt{cd}}\geq \dfrac{2}{a+b} +\dfrac{2}{c+d}=\dfrac{2(a+b+c+d}{(a+b)(c+d)}=VP$

Giải thích mình đoạn tô đỏ, không hiểu đoạn đó lắm

$\sum \dfrac{(2+x)^2}{2+x^2}\leq 8 \Leftrightarrow \sum \dfrac{x^2+2+2(2x+1)}{x^2+2}\leq 8 \Leftrightarrow \sum \dfrac{2x+1}{x^2+2}\leq \dfrac{5}{2} \Leftrightarrow \sum \dfrac{x^2+2-(x-1)^2}{x^2+2} \leq \dfrac{5}{2}$

Rồi chuyển vế là ra cái kia

1) Cho hai tập hợp số nguyên dương phân biêt mà mỗi số đều nhỏ hơn $n.$ Chứng minh rằng nếu tổng số phần tử của hai tập hợp không nhỏ hơn $n$ thì có thể chọn được trong mỗi tập hợp một phần tử sao cho tổng của chúng bằng $n.$

2) Có $20$ người quyết định đi bơi thuyền bằng $10$ chiếc thuyền đôi. Biết rằng nếu hai người $A$ và $B$ mà không quen nhau thì tổng số những người quen của $A$ và những người quen của $B$ không nhỏ hơn $19.$ Chứng minh rằng có thể phân công họ vào các thuyền đôi sao cho mỗi thuyền đều là hai người quen nhau.

3) Cho các số tự nhiên từ $1$ đền $2009.$ Hỏi có thể chọn ra nhiều nhất là bao nhiêu số sao cho tổng của hai số bất kì trong chúng không chia hết cho hiệu của nó?