nguyenthehoan

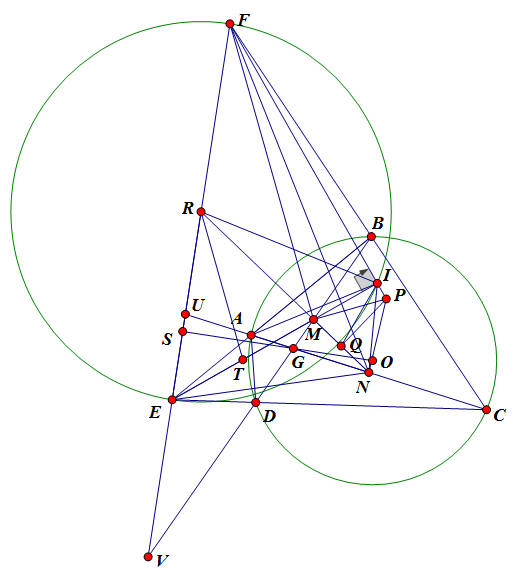
             Problem. Cho tam giác $ABC$.Tâm ngoại tiếp $O$. Đường tròn nội tiếp $(I)$ tiếp xúc $BC,CA,AB$ tại $M,N,P$. Đường tròn bàng tiếp các góc $A,B,C$ tiếp xúc $BC,CA,AB$ tại $D,E,F$. Gọi $H$ là trực tâm tam giác $DEF$ và $J$ là giao điểm của $AI$ và $EF$.Đường thẳng $JM$ cắt $AH$ tại điểm $A'$. Xác định tương tự các điểm $B',C'$. Gọi $A", B",C"$ thứ tự là trung điểm các cạnh $NP,PM,MN$. Chứng minh rằng các đường thẳng qua $A",B",C"$ thứ tự song song với $A'D,B'E,C'F$ đồng quy tại một điểm nằm trên $OI$

Cho tam giác ABC nhọn,trực tâm H, trọng tâm G, từ C kẻ đường thẳng song song với AB cắt đường thẳng HG tại Y.

CMR: $\angle YBA=\angle BAC$

Em xem lại đi. Hình như đề bài sai rồi nhé.

Tồn tại hay không số n có dạng $n= p_{1}^{a_{1}} p_{2}^{a_{2}} .... p_{2000}^{a_{n}} $ .  thỏa    $p_{1}^{a_{1}} p_{2}^{a_{2}} .... p_{2000}^{a_{n}} \mid  2^{p_{1}^{a_{1}} p_{2}^{a_{2}} .... p_{2000}^{a_{n}}} +1  $ trong đó p_k là các số nguyên tố, a_k bất kì.

Ta sẽ chứng minh bằng qui nạp rằng với mọi $k \in {N}$ tồn tại một số nguyên dương $n$ có đúng $k$ ước nguyên dương phân biệt và thỏa mãm điều kiện $n| 2^{n}+1$

Thật vậy, với $k=1$, hiển nhiên ta có $n=3$ thỏa mãn.

Giả sử với $k$ ta đã chọn được số $n_k=3^{a}.b$, trong đó $b$ có đúng $k-1$ ước nguyên tố.

Với $k+1$, ta sẽ chọn $n_{k+1}=3^{a+1}.b.p=3n_k.p$ với $p$ là số nguyên tố không chia hết $b$.

Ta cần chứng minh tồn tại một số nguyên tố $p$ thỏa mãn

$p$ là ước của $2^{3n_k}+1$ nhưng không là ước của $2^{n_k}+1$.

Hay ta sẽ chứng minh, với $a \in N, a=2^{n_k}$ thì tồn tại số nguyên tố $p$ là ước của $a^{3}+1$ nhưng không là ước của $a+1$.

Thật vậy, $a^{3}+1=(a+1)(a^{2}-a+1$ Gọi $d=(a^{2}-a+1,a+1)\Rightarrow d|3a\Rightarrow d=(3,a+1)$

Ta có $3|a+1$ nên $a^{2}-a+1$ không chia hết cho $9$, chọn $p$ là ước nguyên tố bất kì của 

$\frac{a^{2}-a+1}{3}$, ta có điề phải chứng minh.

Vậy ta tìm được $n$ có $k+1$ ước nguyên tố thỏa mãn đề bài.

Vậy bài toán được chứng minh. Với $k=2000$ ta có bài toán trên.

Cho tứ giác $ABCD$ nội tiếp $(O)$. $AB,CD$ giao nhau tại $E$, $AD,BC$ giao nhau tại $F$. $M,N$ lần lượt là trung điểm của $BD,AC$. Đường thẳng qua $F$ vuông góc với $ME$ cắt trung trực của $MN$ tại $P$. Chứng minh $MF$ vuông góc $MP$.

Theo bổ đề Gauss ta có $MN$ đi qua trung điểm $R$ của $EF$.

Gọi $G$ là giao điểm của $AC,BD$. $U,V$ là các giao điểm của $AC,BD$ với $EF$.

Khi đó ta có $(UG,AC)=(VG,DB)=-1$ nên 

$\overline{GU}.\overline{GN}=\overline{GA}.\overline{GC}=\overline{GB}.\overline{GD}=\overline{GV}.\overline{GM}$

Do đó $MNUV$ nội tiếp. Do đó $\overline{RM}.\overline{RN}=\overline{RP}.\overline{RQ}$

Mặt khác do $(UV,EF)=-1\Rightarrow \overline{RU}.\overline{RV}=RE^{2}$.

Do đó $RE^{2}=\overline{RM}.\overline{RN}$ nên $\Delta REM\sim \Delta RNE$

Suy ra $\widehat{REM}=\widehat{RNE}$ Gọi $I$ là giao $FP$ và $EM$. Khi đó góc $EIF$ vuông nên $\widehat{REM}=\widehat{RNE}=\widehat{EIR}$

Vậy $RENI$ nội tiếp. $\Rightarrow \Delta RME\sim \Delta IMN$

Gọi $T$ là trung điểm của $ME$ và $Q$ là trung điểm của $MN$ thì 

$\Rightarrow \Delta RMT\sim \Delta IMQ$

$\Rightarrow \widehat{MIQ}=\widehat{MRT}=\widehat{RMF}$  (vì $RT//FM$)

Mà $MIPQ$ nội tiếp nên $\widehat{MPQ}=\widehat{MIQ}=\widehat{RMF}$

Từ đó kết hợp $PQ \perp MN$ ta có ngay $\widehat{FMP}=90^{\circ}$

Dpcm.

Bài toán: Cho tam giác ABC nội tiếp đường tròn tâm O và điểm P bất kì nằm trong tam giác .Vẽ trung trực của AB,AC cắt AP tại E,F. Qua E kẻ đường thẳng song song AB và cắt tiếp tuyến tại Bcủa $(O)$ ở M. Qua F kẻ đường thẳng song song AC cắt tiếp tuyến tại C của $(O)$ ở N. Vẽ đường tròn ngoại tiếp 2 tam giác ABM và ACN .Gỉa sử MN giao $(ABM)$ tại P,giao $(ACN)$ tại Q. 

         CMR :PB và CQ giao nhau tại một điểm nằm trên đường tròn $(O)$

Bài toán phải sửa lại thành $MN$ giao $(ABM)$ tại $Q$ và $(ACN)$ tại $P$ (như hình vẽ)

Chứng minh.

Ta nhận thấy rằng, để chứng minh $PB, CQ$ cắt nhau trên $(O)$, ta cần chứng minh hai tam giác 

$ABP$ và $ACQ$ đồng dạng.

Ta có $\angle ABM=\angle ABC+\angle MBC=\angle ABC+\angle BAC$

Mà tứ giác $ABMQ$ nội tiếp nên từ trên ta có $\angle AQP=\angle ACB$

Chứng minh tương tự ta có $\angle APQ=\angle ABC$. Do đó $\Delta APQ\sim \Delta ABC$

$\Rightarrow \angle BAP=\angle CAQ$ và $\frac{AP}{AQ}=\frac{AB}{AC}$.

Từ đó ta có $\Delta BAP\sim \Delta CAQ$

Suy ra $\angle ABP=\angle ACQ$. Từ đó ta có ngay $BP,CQ$ cắt nhau trên $(O)$.

Bài toán được chứng minh.

=================================================

P/s. Làm xong mới thấy bài này cho giả thiết về $E,F$ không hiểu để làm gì. Chỉ cần $M,N$ trên các tiếp tuyến tại $B,C$ là đủ.

Kỉ niệm 10 năm sinh nhật diễn đàn và kỉ niệm 1 năm mình tham gia diễn đàn.

Em cám ơn anh Ispectorgadget đã giúp em chuyển định dạng pdf./

 mo rong tu 1 bai toan .pdf   463.07K   830 Số lần tải

Cho tam giác ABC nội tiếp (O), E là 1 điểm di động trên (O). Các tiếp tuyến tại B và C thứ tự cắt AE tại M và N. CM cắt BN tại F. Chứng minh rằng EF luôn đi qua 1 điểm cố định

Trước hết ta phát biểu hai bổ đề quan trọng sau.

Bổ đề 1. Cho tam giác $ABC$ nội tiếp $(O)$, các tiếp tuyến tại $B,C$ cắt nhau tại $D$. Gọi $S$ là giao điểm của $AD$ và $BC$. Khi đó ta có $\frac{SB}{SC}=(\frac{AB}{AC})^{2}$

.Đây là hệ thức quen thuộc về đường đối trung trong tam giác.

================================================

Bổ đề 2. Cho hai đường thẳng $a$ và $a'$ cắt nhau tại $O$. Trên $a$ lấy các điểm $A,B,C$ và trên $a'$ lấy các điểm $A',B',C'$ sao cho $AA',BB',CC'$ không song song. Khi đó $AA',BB',CC'$ đồng quy khi và chỉ khi $(OA,BC)=(OA',B'C')$ 

.Đây là hệ thức cơ bản về tính chất về tỉ số kép.

================================================

Áp dụng hai bổ đề trên, ta sẽ chứng minh rằng đường thẳng $EF$ đi qua giao điểm $X$ của $AD$ và $BC$, trong đó $D$ là giao điểm các tiếp tuyến tại $B$ và $C$ của $(O)$.

 EF co dinh.png   24.01K   18 Số lần tải

Trong bài toán, giả sử $E$ thuộc cung nhỏ $BC$, các trường hợp khác chứng minh tương tự.

Áp dụng bổ đề 2 với các đường thẳng $BC$ và $MN$ cắt nhau tại $P$, để chứng minh $EX,CM,BN$ đồng quy, ta phải chứng minh $(PX,CB)=(PE,MN)$ (1)

Gọi $K$ là giao điểm của $DE$ và $BC$. Xét phép chiếu tâm $K$, do tính chất bảo toàn tỉ số kép,ta có $(PE,MN)=(PK,BC)$.

Do đó để chứng minh (1), ta phải chứng minh $(PK,BC)=(PX,CB)$, hay 

$\frac{PB}{PC}.\frac{KC}{KB}=\frac{PC}{PB}.\frac{XB}{XC}\Leftrightarrow (\frac{PB}{PC})^{2}=\frac{XB}{XC}.\frac{KB}{KC}$. (2)

Áp dụng bổ đề 1 cho các tam giác $ABC$ và $EBC$ nội tiếp $(O)$ có $D$ là giao các tiếp tuyến tại $B,C$ và $K,X$ là giao $ED,AD$ với $BC$ ta có 

$\frac{XB}{XC}=(\frac{AB}{AC})^{2},\frac{KB}{KC}=(\frac{EB}{EC})^{2}$

Do đó để chứng minh (2),ta phải chứng minh $\frac{PB}{PC}=\frac{AB}{AC}.\frac{EB}{EC}$

Ta có $\Delta EPB\sim \Delta CPA\Rightarrow \frac{PB}{PA}=\frac{EB}{CA}$

Tương tự $\Delta APB\sim \Delta CPE\Rightarrow \frac{AP}{CP}=\frac{AB}{EC}$

Nhân các vế hai đẳng thức này,ta nhận được điều phải chứng minh.

  Bài toán :Cho $\Delta ABC$ có đường tròn $(I)$ nội tiếp trong tam giác và tiếp xúc với $BC,CA,AB$ tại $D,E,F$. Vẽ đường tròn $(I_{1})$ đi  qua $I$ và tiếp xúc với AB,AC .Vẽ đường tròn $(I_{2})$ đi qua $I$ và tiếp xúc với AB,BC. Vẽ đường tròn $(I_{3})$ đi qua $I$ và tiếp xúc với AC,BC. Gọi $X,Y,Z$ lần lượt là giao điểm thứ 2 khác $I$ của các cặp đường tròn $(I_{2}),(I_{3});(I_{1}),(I_{3});(I_{1}),(I_{2})$. Gọi $M,N,P$ theo thứ tự là tâm đường tròn ngoại tiếp các tam giác $AIX,BIY,CIZ$.

                   CMR: $M,N,P$ thẳng hàng .

Thực hiện phép nghịch đảo cực $I$ với phương tích bất kì, ta có bài toán đã cho tương đương với bài toán sau.

Bài toán. Cho tam giác $ABC$,trực tâm $H$. Gọi $(X),(Y),(Z)$ thứ tự là các đường tròn ngoại tiếp các tam giác $BHC,CHA,AHB$. Các tiếp tuyến chung ngoài của các cặp đường tròn $(X),(Y),(Z)$ cắt nhau tạo thành tam giác $PQR$. Chứng minh rằng $AP,BQ,CR$ đồng quy.

 dôi xa.png   29.6K   23 Số lần tải

 

Để chứng minh bài toán này, ta cần đến bổ đề đơn giản sau.

Cho hai tam giác $ABC$ và $DEF$ có các cặp cạnh $(AB,DE),(BC,EF),(CA,FD)$ tương ứng song song. Khi đó ta có các đường thẳng $AD,BE,CF$ đồng quy tại tâm vị tự biến tam giác này thành tam giác kia.

 

Trở lại bài toán, ta sẽ chứng minh hai tam giác $ABC$ và $PQR$ có các cặp cạnh tương ứng song song.

Ta có tính chất quen thuộc. Tâm ngoại tiếp các tam giác $HBC,HCA,HAB$ thứ tự là đối xứng của tâm $O$ ngoại tiếp tam giác $ABC$ qua $BC,CA,AB$ và 

Gọi $M,N$ là các tiếp điểm của tiếp tuyến chung của $(Z),(Y)$ trên $(Z),(Y)$

Khi đó Ta có $ZM=YN=R$ và $ZM//YN$ nên tứ giác $ZMNY$ là hình bình hành, thêm nữa $\widehat{ZMN}=90^{\circ}$ nên tứ giác này là hình chữ nhật,nên $MN//YZ$

Mà $YZ$ là đường trung trực của $AH$ và $AH\perp BC$ nên ta có $MN//BC$ hay $QR//BC$

 

Chứng minh tương tự ta có ngay điều phải chứng minh.

Theo anh thấy trong hình vẽ của anh thì đường cố định mà $A'E$ tiếp xúc là 1 elip

Elip ạ??   Thảo nào em vẽ mãi không ra...Nói đến Elip thì em chịu rồi....Thực ra bài toán trên là em lấy ý tưởng từ một bài trên THTT.

Anh phát hiện ra thêm 1 bài toán này:

Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định và $BC$ cố định, $A$ di động. Vẽ đường cao $BE$ và đường kính $AA'$ của $(O)$.

Chứng minh rằng: $A'E$ tiếp xúc 1 đường cố định.

 

Spoiler

Chuẩn bị thi thố thế nào rồi nguyenthehoan

Em vẫn bình thường thôi ạ.Dạo này liên hoan suốt .Mà anh Hân ơi, bài trên của anh là đường tròn nào thế ạ? Em vẽ hình cũng phát hiện ra một đường tròn, nhưng nó không cố định thì phải..Nó chỉ lệch có vài mm thôi!!

Bài toán. Cho $p$ là một số nguyên tố cho trước. Xét dãy số $(a_n)$ thỏa mãn điều kiện.

i) $a_k=k, \forall k=0,1,...,p-1$

ii) $a_n=a_{n-1}+a_{n-p},\forall n\geq p$

Tìm số dư trong phép chia $a_{p^{2014}+1}$ cho $p$.

Mình vừa nghĩ ra bài toán khá thú vị!!!

 

Bài toán. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ có $B,C$ cố định, còn $A$ di chuyển trên đường tròn.Gọi $\Delta$ là đường thẳng qua $O$ cắt $AB,AC$ tại $X,Y$ thỏa mãn $OX=OY$. Đường tròn đường kính $BY$ cắt $(O)$ tại $P$ và cắt đường tròn Ole của tam giác $ABC$ tại $Q$.

a) Chứng minh rằng khi $A$ thay đổi trên đường tròn $(O)$, thì $PQ$ luôn đi qua một điểm cố định.

b) Chứng minh rằng khi $A$ thay đổi trên đường tròn $(O)$, thì đường thẳng kẻ qua $A$ và vuông góc với $\Delta$ luôn đi qua một điểm cố định.

 

Cho tam giác $ABC$. Điểm $M$ thuộc đoạn $BC$. Gọi $P$ là giao điểm của đường thẳng qua $M$ vuông góc $AB$ và đường thẳng qua $B$ vuông góc $BC$, $Q$ là giao của đường thẳng qua $M$ vuông góc $AC$ và đường thẳng qua $C$ vuông góc $BC$. Lấy $M'$ trên $BC$ để $AM'$ vuông góc $PQ$. CM $BM$=$M'C$.

                                                     .......................................................

(1 bài trong tài liệu lê quý đôn của thầy Trần Quang Hùng, mình tìm đc 1 lời giải nhưng nó ko hay

Ta xét trường hợp khi $P,Q$ nằm ngoài tam giác $ABC$ (các trường hợp khác chứng minh tương tự)

 ss.png   25.03K   136 Số lần tải

Gọi $S$ là điểm trên đoạn $BC$ sao cho $BS=CM$. Ta sẽ chứng minh $AS\perp PQ$

Gọi $X$ là giao điểm của $MP$ và $BC$ và $O$ là trung điểm của $AM$.

Ta có $PB^{2}=\overline{PX}.\overline{PM}$. Xét phương tích của $P$ với đường tròn đường kính $AM$ ta có ngay $\overline{PX}.\overline{PM}=PO^{2}-AO^{2}$. Do đó $PB^{2}=PO^{2}-AO^{2}$

Lại theo công thức đường trung tuyến ta có $PO^{2}=\frac{PA^{2}+PM^{2}}{2}-AO^{2}$

Vậy $2PB^{2}=PA^{2}+PM^{2}-AM^{2}$. Một cách tương tự ta có 

$2QC^{2}=QA^{2}+QM^{2}-AM^{2}$.

Do đó $2(PB^{2}-QC^{2})=AP^{2}-AQ^{2}+PM^{2}-QM^{2}$

$\Rightarrow AP^{2}-AQ^{2}=MC^{2}-MB^{2}+PB^{2}-QC^{2}$ (1)

Ta có $SP^{2}-SQ^{2}=SB^{2}+PB^{2}-SC^{2}-QC^{2}=MC^{2}-MB^{2}+PB^{2}-QC^{2}$  (2)

Từ (1) và (2) ta có $AP^{2}-AQ^{2}=SP^{2}-SQ^{2}$

Do đó ta có $AS\perp PQ$. Dpcm.

Cho tam giác ABC nội tiếp (O) và ngoại tiếp (I). Đường tròn (I) tiếp xúc BC tại D. Gọi J là trung điểm AI, E là trung điểm cung BC không chứa A. Đường tròn tâm J đường kính AI cắt (O) tại M, OM cắt DI tại K. Chứng minh rằng JK // DE  

 ss.png   27.72K   20 Số lần tải

Trước hết ta chứng minh rằng: $E,D,M$ thẳng hàng.

Vẽ đường kính $AS$. Vì $M$ thuộc đường tròn đường kính $AI$ nên $\widehat{AMI}=90^{\circ}$

Do đó ta có $M,I,S$ thẳng hàng.

Ta có $\widehat{EBC}=\widehat{ECA}=\widehat{EAB}$ nên nếu gọi $F$ là giao điểm của $AI$ và $BC$ thì $\Delta EBF\sim \Delta EAB\Rightarrow \frac{EB}{EA}=\frac{BF}{BA}$

Lại có $\frac{IF}{IA}=\frac{BF}{BA}$ (tính chất phân giác) 

Do đó $\frac{EI}{EA}=\frac{IF}{IA}$. Lại do $EI=EB=EC$ nên ta có $\frac{IF}{IA}=\frac{IE}{EA}\Rightarrow IF.EA=IA.IE$.  (1)

Lại có $\widehat{AFB}=\widehat{ASE}$ (cộng cung) nên ta có $\Delta ASE\sim \Delta IFD\Rightarrow IF.AE=ID.AS$ (2)

Từ (1) và (2) ta có $IE.IA=ID.AS$. Lại có $\widehat{DIE}=\widehat{IAS}$ Nên 

$\Delta DIE\sim \Delta IAS \Rightarrow \widehat{DEI}=\widehat{ISA}=\widehat{IEM}$

Do đó $D,M,E$ thẳng hàng.

Theo trên ta đã có $\widehat{DIE}=\widehat{IAS}$. Mà $\widehat{IAS}=\widehat{JAO}=\widehat{JMO}$ (do $OJ$ là trung trực của $OM$)

Suy ra $\widehat{JMO}=\widehat{DIE}=\widehat{JIK}$ nên tứ giác $MJKI$ nội tiếp.

Suy ra $\widehat{KJI}=\widehat{KMI}=\widehat{OMS}=\widehat{OSM}=\widehat{IEM}$

Do đó $JK//ME$. Hay $JK//DE$.

Cho tam giác $ABC$. Định nghĩa đường tròn $(O_a)$  là đường tròn tiếp xúc với $AB,AC$ và $(ABC)$. $(O_a)$ tiếp xúc $(ABC)$ tại $X$, định nghĩa tương tự cho $Y,Z$. Gọi $I$ là đường tròn nội tiếp $\Delta ABC$, $(I)$ tiếp xúc $BC$ tại $A_1$, $AI$ cắt $BC$ tại $N_1$. Chứng minh rằng $A_1,N_1,Y,Z$ đồng viên.

Mình chưa nghĩ được cách hay nên post cách này nhé!

 

Ta phát biểu các bổ đề sau.

 

Bổ đề 1: Cho tam giác $ABC$ với $AM,AN$ là hai đường đẳng giác góc $A$. ($M,N$ trên $BC$).

 

Khi đó ta có hệ thức $\frac{MB}{MC}.\frac{NB}{NC}=(\frac{AB}{AC})^{2}$

(Đây là định lí quan trọng về các đường đẳng giác, các bạn có thể dùng tam giác đồng dạng hoặc diện tích để chứng minh)

 

Bổ đề 2 :Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Tiếp tuyến của $(O)$ tại $A$ cắt $BC$ tại

 

$P$. Khi đó $\frac{PB}{PC}=(\frac{AB}{AC})^{2}$

(Chứng minh chỉ dựa vào các tam giác đồng dạng $APB$ và $CPA$)

 

Bổ đề 3: Cho tam giác $ABC$. Gọi $I$ là tâm nội tiếp.$U,V$ là tâm các đường tròn Mixtlinear trong với góc $B,C$. Khi đó $UV,BC$ và đường thẳng qua $I$ và vuông góc với $AI$ đồng quy.

 

Chứng minh cho bổ đề 3.  bo de 3.png   26.4K   16 Số lần tải

Gọi $D,E$ là hình chiếu của $U,V$ trên $BC$. Khi đó theo định lí Lyness ta có ngay $ID\perp IC, IE\perp IB$.

 

Gọi $F$ là giao điểm của đường thẳng qua $I$ vuông góc $AI$ và $BC$. Ta sẽ chứng minh 

 

$\frac{FD}{FE}=\frac{UD}{VE}$. Khi đó hiển nhiên ta có ngay $U,V,P$ thẳng hàng.

 

Ta có các góc bằng nhau. $\widehat{FIB}=\widehat{GIE},\widehat{BID}=\widehat{EIC}$

 

Nên trong tam giác $FIC$, hai đường $ID,IG$ đẳng giác. Nên theo đề 1:

 

$\frac{DF}{DC}.\frac{GF}{GC}=(\frac{IF}{IC})^{2}$.

 

Một cách tương tự ta có $\frac{EF}{EB}.\frac{GF}{GB}=(\frac{IF}{IB})^{2}$

 

Chia hai vế hai đẳng thức trên cho ta 

$\frac{EB}{DC}.\frac{FD}{FE}.\frac{GB}{GC}=(\frac{IB}{IC})^{2}$.

$\Rightarrow \frac{FD}{FE}=\frac{IB^{2}}{IC^{2}}.\frac{GC}{GB}.\frac{DC}{EB}$.  (1)

 

Mặt khác ta có $\Delta UDI\sim \Delta DCI\Rightarrow \frac{UD}{ID}=\frac{CD}{CI}$

Tương tự ta có $\frac{VE}{IE}=\frac{EB}{IB}$.

 

Suy ra $\frac{UD}{VE}=\frac{IB}{IC}.\frac{CD}{BE}.\frac{ID}{IE}$.  (2)

 

Do đó từ (1) và (2) ta phải chứng minh 

 

$\frac{IB}{IC}.\frac{CD}{BE}.\frac{ID}{IE}=\frac{IB^{2}}{IC^{2}}.\frac{GC}{GB}.\frac{DC}{EB}$

 

$\Leftrightarrow \frac{ID}{IE}=\frac{IB}{IC}.\frac{GC}{GB}$

 

$\Leftrightarrow \frac{ID.IC}{IE.IB}=\frac{GC}{GB}$

 

$\Leftrightarrow \frac{DC.r}{EB.r}=\frac{GC}{GB}$

 

$\Leftrightarrow \frac{DC}{EB}= \frac{AC}{AB}$. 

 

Gọi $R,S$ là đối xứng của $D,E$ qua $IC,IB$. Ta có $DERS$ là hình bình hành nên $RS//BC$

 

Suy ra $\frac{DS}{CR}=\frac{AB}{AC}\Rightarrow \frac{EB}{DC}=\frac{AB}{AC}$

 

Bổ đề 3 được chứng minh.

 

Trở lại bài toán của ta.  ly.png   30.45K   18 Số lần tải

 

Ta có $Z,Y$ lần lượt là các tâm vị tự trong biến $(U), (V)$ thành $(O)$.

 

Gọi $P$ là giao điểm của đường thẳng qua $I$ vuông góc $AI$ với $BC$. Khi đó theo bổ đề 3 ta có ngay $P$ là tâm vị tự ngoài của $(U), (V)$

 

Do đó $Z,P,Y$ thẳng hàng.

 

Khi đó ta có $PZ.PY=PB.PC=PI^{2}=PN_1.PA_1$.

 

Ta có ngay $N_1,A_1,Y,Z$ đồng viên.