1) Tính đạo hàm của hàm số f(x) biết $\int_{0}^{x}te^{f(t)}dt=e^{f(x)}$
2) Cho biết $\int_{0}^{\sqrt{2}}xf(x^2)=4;\int_{2}^{3}f(z)dz=2;\int_{9}^{16}\frac{f(\sqrt{t})}{\sqrt{t}}=3...TinhI=\int_{0}^{4}f(x)$
- leminhnghiatt yêu thích
$\frac{kudoshinichihv99}{15-10-1999}$
$K69A,THPT Hùng Vương,Phú Thọ$
$\sqrt{Kỉ niệm ngày 14-8}$
 Nam
Nam
 Gửi bởi kudoshinichihv99
trong 15-01-2017 - 08:38
Gửi bởi kudoshinichihv99
trong 15-01-2017 - 08:38
1) Tính đạo hàm của hàm số f(x) biết $\int_{0}^{x}te^{f(t)}dt=e^{f(x)}$
2) Cho biết $\int_{0}^{\sqrt{2}}xf(x^2)=4;\int_{2}^{3}f(z)dz=2;\int_{9}^{16}\frac{f(\sqrt{t})}{\sqrt{t}}=3...TinhI=\int_{0}^{4}f(x)$
 Gửi bởi kudoshinichihv99
trong 06-08-2016 - 15:44
Gửi bởi kudoshinichihv99
trong 06-08-2016 - 15:44
Bài 469:$\begin{cases} & 3\sqrt{y^3(2x-y)}+\sqrt{x^2(5y^2-4x^2)}=4y^2 \\ & \sqrt{2-x}+\sqrt{y+1}+2=x+y^2 \end{cases}$
PT1<=>$4y^2=3\sqrt{y^2(2xy-y^2)}+\sqrt{x^2(5y^2-4x^2)}\leq \frac{3(y^2+2xy-y^2)}{2}+\frac{x^2+5y^2-4x^2}{2}<=>(x-y)^2\leq 0=>x=y=>PT2<=>\sqrt{2-x}+\sqrt{x+1}=-(2-x)(x+1)=>...$
 Gửi bởi kudoshinichihv99
trong 05-08-2016 - 15:30
Gửi bởi kudoshinichihv99
trong 05-08-2016 - 15:30
Bài 14: (THPTQG 2016)
Một CLLX treo vào một điểm cố định dao động điều hòa theo phương thẳng đứng. Tại thời điểm lò xo dãn $2$ cm, tốc độ của vật là $4\sqrt{5}v$ (cm/s). Tại thời điểm lò xo dãn $4$ cm, tốc độ của vật là $6\sqrt{2}v$ (cm/s). Tại thời điểm lò xo dãn $6$ cm, tốc độ của vật là $3\sqrt{6}v$ (cm/s). $g=9,8 (m/s^2)$. Trong một chu kì, tốc độ trung bình của vật trong khoảng thời gian lò xo bị dãn có giá trị gần nhất với giá trị nào dưới đây:
A: $1,26$ (m/s)
B: $1,21$ (m/s)C: $1,43$ (m/s)
D: $1,52$ (m/s)
Bài 15: (THPTQG 2016)
Ở mặt chất lỏng có $2$ nguồn kết hợp đặt tại $A$ và $B$ dao động điều hòa, cùng pha theo phương thẳng đứng. $Ax$ là nữa đường thẳng nằm ở mặt chất lỏng và vuông góc với $AB$. Trên $Ax$ có những điểm dao động với biên độ cực đại, trong đó $M$ là điểm xa $A$ nhất, $N$ là điểm kế tiếp với $M$, $P$ là điểm kế tiếp với $N$ và $Q$ là điểm gần $A$ nhất. Biết $MN=22,25$ cm, $NP=8,75$ cm. Độ dài đoạn $QA$ gần nhất với giá trị nào
A: $1,2$cm
B: $3,1$cm
C: $2,1$cm$\lambda /2$
D: $4,2$cm
Bài 14
Gọi li độ ban đầu của chất điểm là x, A là biên độ
=>$\frac{A^2-x^2}{A^2-(x+2)^2}=10/9;\frac{A^2-(x+2)^2}{A^2-(x+4)^2}=4/3=>x=0,6;A=8(cm)=>\Delta l=1,4 cm=>\omega =10\sqrt{7},T=0,24s=>x=8cos(10\sqrt{7}t+\pi /2)=-1,4=>tmin=6,63.10^{-3}s=>\Delta t=2tmin+T/2=>v=s/\Delta t=1,43m/s$
P/s:Hơi tắt tý, m.n ko hiều thì hỏi nha ![]()
Bài 15
ko biết vẽ hình thì khó làm lắm, mình chỉ nêu hướng ntn:
Chon hệ trục tọa độ Oxy với O là trung điểm AB, ta có các vân cự đại là các đường Hypebol nhận A,B là tiêu điểm với các tiêu cự lần lượt là c1,c2,c3,c4 theo thứ tự tăng $\lambda /2$, các điểm M,N,P,Q thuộc đường thẳng Ax' vuông góc với Ox có cùng hoàng độ OA, bài toán được quy về phương pháp tọa độ trong mặt phẳng lưu ý $MA=\left | c_{1}-\frac{OA^2}{c_{1}} \right |$ NA,PA,QA tương tự, xét MA-NA=22,25;NA-PA=8,75=>$\lambda =4,AO=9$=>OA=2,15
Mấy bài năm nay được mỗi cái trâu bò, không biết còn cách giải nào khác không ![]()
 Gửi bởi kudoshinichihv99
trong 04-08-2016 - 15:16
Gửi bởi kudoshinichihv99
trong 04-08-2016 - 15:16
Giải hệ phương trình
$\left\{\begin{matrix} \sqrt{y^{2} - 8x + 9} - \sqrt[3]{xy + 12 - 6x} = 1\\ \sqrt{2(x - y)^{2} + 10x - 6y + 12} - \sqrt{y} = \sqrt{x + 2} \end{matrix}\right.$
$PT(2)<=>\sqrt{2(x-y+2)^2+2(x+y+2)}=\sqrt{x+2}+\sqrt{y}\leq \sqrt{2(x+y+2)}(BDT B.C.S)=>(x-y+2)^2\leq 0=>x+2=y$
Thay vào 1 là ok
 Gửi bởi kudoshinichihv99
trong 29-07-2016 - 15:29
Gửi bởi kudoshinichihv99
trong 29-07-2016 - 15:29
 Gửi bởi kudoshinichihv99
trong 29-07-2016 - 15:26
Gửi bởi kudoshinichihv99
trong 29-07-2016 - 15:26
c có chắc là $y$ lớn hơn 0 k? Nếu đưa ra ngoài mà $y<0$ thì sẽ phải chuyển thành dấu -
Vì đk $x\geq 3$ với đk này $x^3-3x^2+2\geq 2$=> y>0
P/s Chào em đồng hương ![]()
 Gửi bởi kudoshinichihv99
trong 29-07-2016 - 14:57
Gửi bởi kudoshinichihv99
trong 29-07-2016 - 14:57
giải phương trình:
$x^3+\sqrt{(1-x^2)^3}=x\sqrt{2-2x^2}$
$\frac{1}{1-x^2}=\frac{3x}{\sqrt{1-x^2}}-1$
Cách làm của 2 này đều sử dụng lượng giác hóa
Đặt $x=cosa(0\leq a\leq \pi ).PT1<=>cos^3a+\left | sin^3a \right |=\sqrt{2}.sina.cosa$ Giải pt này đơn giản, phần 2 cũng làm như thế.
Nếu là HS THCS thì đặt $\sqrt{1-x^2}=y=>\left\{\begin{matrix} x^3+y^3=\sqrt{2}xy & \\ x^2+y^2=1 \end{matrix}\right.$ đưa hết về x+y, xy để giải, phần 2 làm tương tự
 Gửi bởi kudoshinichihv99
trong 02-07-2016 - 14:47
Gửi bởi kudoshinichihv99
trong 02-07-2016 - 14:47
Mình vẽ hình ra thấy mỗi vân Hyperbol chỉ cắt Parabol tại $1$ điểm
Hình vẽ của bạn chỉ mang tính minh họa thui. chứ nó có thể cắt nhau tại 2 điểm tùy thuộc vào phương trình của 2 đường đấy
 Gửi bởi kudoshinichihv99
trong 02-07-2016 - 14:45
Gửi bởi kudoshinichihv99
trong 02-07-2016 - 14:45
Mình thấy lời giải trong sách như thế này
Giữa hai vân qua $M$, $N$ còn có $3$ vân cùng loại nên số bậc giao thoa qua $2$ điểm này chênh nhau $4$. Suy ra hiệu số của hiệu $2$ khoảng cách của chúng bằng $4 \lambda$, nên ta có $\lambda =\frac{51-27}{4}=6$ mm $\Rightarrow \frac{\lambda }{2}=3$ mm
Vân qua $M$ có thể viết $MS_1-MS_2=27=9.3=(2.4+1)\frac{\lambda }{2}$
Do hiệu khoảng cách tới hai nguồn bằng số lẻ của nửa bước sóng nên vân giao thoa qua $M$ là vân cực tiểu, vân này ứng với $k=4$$\Rightarrow$ Đáp án:C
Nhưng chỗ bôi đỏ là những chỗ mình thật sự không hiểu
Chỗ bôi đỏ thứ nhất:
Cứ giả sử $2$ nguồn là $u_A=u_B=a\cos \omega t$ đi thì
$u_{M}=2a\cos (\pi.\frac{27}{\lambda})\cos(\omega t-\pi.\frac{d_1+d_2}{\lambda })$
$u_{N}=2a\cos (\pi.\frac{51}{\lambda})\cos (\omega t-\pi.\frac{d_1'+d_2'}{\lambda})$
Vì biên độ tại $M$ bằng biên độ tại $N$ nên ta giải pt $2a\begin{vmatrix} \cos (\pi.\frac{27}{\lambda}) \end{vmatrix}=2a\begin{vmatrix} \cos(\pi.\frac{51}{\lambda}) \end{vmatrix}$
Vậy thì làm sao có được cái chỗ bôi đỏ thứ nhất đó ?
Chỗ bôi đỏ thứ $2$:
Nếu ta viết $M$ như thế thì $k=0,1,2,3,4$. Vậy $M$ phải thuộc vân cực tiểu số $5$ chứ tại sao lại là $4$ ???
Về chỗ thứ nhất thì có vẻ hợp lý vì nếu M thuộc vân cực đại thì $MS_{1}-MS_{2}=k\lambda$ nếu giá trị của k tăng dần thì hiệu khoảng cách cũng tăng dần 1$\lambda$; nếu M thuộc vân cực tiểu thì $MS_{1}-MS_{2}=(2k+1)\lambda/2$ cũng tương tự như thế. Còn chỗ thứ 2 thì có vấn đề
 Gửi bởi kudoshinichihv99
trong 01-07-2016 - 15:17
Gửi bởi kudoshinichihv99
trong 01-07-2016 - 15:17
Bài 8:
. Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 10 cm, dao động theo phương thẳng đứng với phương trình uA = 3cos40πt và uB = 4cos(40πt) (uA và uB tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Hỏi trên đường Parabol có đỉnh I nằm trên đường trung trực của AB cách O 1 đoạn 10cm và đi qua A, B có bao nhiêu điểm dao động với biên độ bằng 5mm (O là trung điểm của AB):
A. 13 B. 14 C. 26 D. 28
P/s Mọi người ủng hộ Pic này của mình với ![]()
 Gửi bởi kudoshinichihv99
trong 01-07-2016 - 15:13
Gửi bởi kudoshinichihv99
trong 01-07-2016 - 15:13
Bài 7:
Một CLLX gồm một vật nhỏ có khối lượng $100$ g, $k=40(N/m)$ đặt trên mặt phẳng ngang không ma sát. Vật nhỏ đang đứng yên tại VTCB, tại $t=0$, tác dụng lực $F=2$ (N) lên vật nhỏ cho con lắc dao động điều hòa đến thời điểm $t=\frac{\pi}{3}$ thì ngừng tác dụng lực $F$. Hỏi biên độ của con lắc sau khi ngừng tác dụng lực $F$ là bao nhiêu ?
Đầu tiên xác định VTCB của con lắc khi dao động với ngoại lực F không đổi:
$x_{0}=\frac{F}{k}=5cm$
Đây cũng chính là biên độ ban đầu của con lắc . Chu kỳ của con lắc là T= $\frac{\pi }{10}$
Thành lập pt dao động ta thấy sau $t=\frac{\pi}{3}$ thì con lắc ở vị trí x= 2,5cm với vận tốc v= 50$\sqrt{3}$ cm/s
khi không còn lực tác dụng F thì VTCB lại trở về O => li độ của con lắc là x=7,5 cm với vận tốc v= 50$\sqrt{3}$ cm/s
=> Biên độ mới A' =8,66 cm
 Gửi bởi kudoshinichihv99
trong 30-06-2016 - 14:32
Gửi bởi kudoshinichihv99
trong 30-06-2016 - 14:32
Bài 5
: Hai vật dao động điều hòa dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ Ox sao cho không va chạm vào nhau trong quá trình dao động. Vị trí cân bằng của hai vật đều ở trên một đường thẳng qua gốc tọa độ và vuông góc với Ox. Biết phương trình dao động của hai vật lần lượt là x1 = 4cos(4πt + π/3) cm và x2 = 4$\sqrt{2}$ cos(4πt + π/12) cm. Tính từ thời điểm t1 = 1/24 s đến thời điểm t2 = 1/3 s thì thời gian mà khoảng cách giữa hai vật theo phương Ox không nhỏ hơn 2$\sqrt{3}$ cm là bao nhiêu?
A. 1/8 s. B. 1/12 s. C. 1/9 s. D. 1/6 s.
Bài 6
Trên mặt một chất lỏng, có hai nguồn sóng kết hợp O1, O2 cách nhau l = 24cm, dao động theo cùng một phương với phương trình $x=Acos(\omega t)$(t tính bằng s A tính bằng mm) Khoảng cách ngắn nhất từ trung điểm O của O1O2 đến các điểm nằm trên đường trung trực của O1O2 dao động cùng pha với O bằng q = 9cm. Số điểm dao động với biên độ bằng O trên đoạn O1O2 là ?
A. 18 B. 16 C. 20 D. 14
P/S Các bạn tích cực đăng bài nhé ![]()
 Gửi bởi kudoshinichihv99
trong 30-06-2016 - 14:24
Gửi bởi kudoshinichihv99
trong 30-06-2016 - 14:24
Bài 4:
Giả sử một vệ tinh dùng trong truyền thông đang đứng yên so với mặt đất ở một độ cao xác định trong mặt phẳng xích đạo Trái Đất đi qua kinh độ số $0$. Coi Trái Đất như một quả cầu, bán kính là $6370$ km, khối lượng là $6.10^{24}$ kg và chu kì quay quanh trục của nó là $24$h, hằng số hấp dẫn $G=6,67.10^{-11}$ ($N.m^2/kg^2$). Sóng cực ngắn ($f>30$ MHz) phát từ vệ tinh truyền thẳng đến các điểm nằm trên xích đạo Trái Đất trong khoảng kinh độ nào nêu dưới đây
A: Kinh độ $79^o20'$ Đ đến kinh độ $79^o20'$ T
B: Kinh độ $83^o20'$ T đến kinh độ 83^o20'$ Đ
C: Kinh độ $85^o20'$ Đ đến kinh độ $85^o20'$ T
D: Kinh độ $81^o20'$ T đến kinh độ $81^o20'$ Đ
Muốn một vệ tinh ở trong mặt phẳng xích đạo và đứng yên so với mặt đất, nó phải chuyển động tròn xung quang Quả đất cùng chiều và cùng vận tốc $\omega$ như Trái đất quay xung quanh trục của nó với chu kỳ T=24h.
Gọi vận tốc dài của vệ tinh trên quỹ đạo là v, độ cao của nó so với mặt đất là h. Vì chuyển động tròn nên vệ tinh có gia tốc hướng tâm bằng:
+ Fht=,$\frac{mv^2}{(h+R)^2}$
lực này chính là lực hấp dẫn của Trái đất đối với vệ tinh
+ Fhd=$\frac{GmM}{(h+R)^2}$. Từ hai biểu thức trên suy ra ,$\frac{mv^2}{(h+R)^2}$ = $\frac{GmM}{(h+R)^2}$.
Vì: v=(h+R)$\omega$2. mà $\omega =\frac{2\pi }{T}$, với T=24h ta có
h+R=42322km
Vậy, độ cao của vệ tinh so với mặt đất là: h=42322-6370=35952 km
Đối với súng cực ngắn, ta có thể xem như sóng truyền thẳng từ vệ tinh xuống mặt đất. .
Vẽ hình ta tính được vùng nhận được tín hiệu từ vệ tinh nằm trong khoảng
Từ kinh độ 81020’T đến kinh độ 81020’Đ
P/s hai bài này hay đấy ![]()
 Gửi bởi kudoshinichihv99
trong 30-06-2016 - 07:16
Gửi bởi kudoshinichihv99
trong 30-06-2016 - 07:16
Bài 3:
Hai chất điểm $M$ và $N$ có cùng khối lượng dao động điều hòa cùng tần số dọc theo hai đường thẳng song song kề nhau và song song với trục tọa độ $Ox$. Biên độ của $M$ là $6$ cm, của $N$ là $8$ cm. Trong quá trình dao động, khoảng cách lớn nhất giữa $M$ và $N$ theo phương $Ox$ là $10$cm. Mốc thế năng tại vị trí cân bằng $O$. Ở thời điểm mà $M$ có động năng bằng thế năng, tỉ số động năng của $M$ và động năng của $N$ là?
Một cách giải theo toán học :
Gọi phương trình dao động của M,N lần lượt là:
$x_{1}=6cos(\omega t+\varphi _{1});x_{2}=8cos(\omega t+\varphi _{2})=>d_{max}=\left |x_{2}-x_{1} \right |_{max}=\sqrt{8^2+6^2+2.8.6.cos(\varphi _{2}-\varphi _{1}-\pi )}=10=>\varphi _{2}-\varphi _{1}-\pi =\pi /2+k\pi =>\varphi _{2}-\varphi _{1}=3\pi /2(-\pi \leq \varphi\leq \pi )=>x_{2}=8cos(\omega t+\varphi _{1}+3\pi /2)=8sin(\omega t+\varphi _{1})=\frac{8}{\sqrt{2}}=>E_{đ1}/E_{đ2}=9/16$
P/s Bài 4 để đọc lý thuyết đã ![]()
 Gửi bởi kudoshinichihv99
trong 29-06-2016 - 18:32
Gửi bởi kudoshinichihv99
trong 29-06-2016 - 18:32
Bình tĩnh thui a ![]()
Bài 3
Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang cân ABCD (AD // BC) có phương trình đường thẳng AB: x – 2y + 3 = 0 và đường thẳng AC= y – 2 = 0. Gọi I là giao điểm của hai đường chéo AC và BD. Tìm tọa độ các đỉnh của hình thang cân ABCD, biết IB=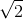 IA, hoành độ điểm I: xI>-3 và M(-1;3) nằm trên đường thẳng BD
IA, hoành độ điểm I: xI>-3 và M(-1;3) nằm trên đường thẳng BD
Bài 4
Trong mặt phẳng với hệ trục toạ độ Oxy cho hình chữ nhật ABCD có diện tích bằng 12, tâm I là giao điểm của đường thẳng d1: x- y – 3 = 0 và d2: x + y - 6 = 0. Trung điểm của một cạnh là giao điểm của d1 với trục Ox. Tìm toạ độ các đỉnh của hình chữ nhật.

Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học

 Tìm kiếm
Tìm kiếm