doraemon123

Cho tam giác ABC,. Hai điểm M và N theo thứ tự di chuyển trên các tia đối của BA và CA sao cho BM=CN .Gọi I là trung điểm của MN. Hỏi I di động trên đường nào??

Cho 3 số thực dương x,y,z>1 thỏa mãn: $x+y+z=xyz$. Tìm GTNN của:

A=$\frac{y-2}{x^2}+\frac{z-2}{y^2}+\frac{x-2}{z^2}$

Giải phương trình
$\sqrt{x^2+x-1} + \sqrt{x-x^2+1} = x^2-x+2$

Ta có: $\sqrt{x^2+x-1}+\sqrt{x-x^2+1}=\sqrt{x^2+x-1}.1+\sqrt{x-x^2+1}.1\leq \frac{x^2+x-1+1}{2}+\frac{x-x^2+1+1}{2}=x+1$

Dấu ''='' xảy ra khi x=1

Mà $x^2-x+1\geq x+1$. Dấu ''='' xảy ra khi x=1

Vậy nghiệm của pt là x=1

Cho a,b,c là các số thực không âm có tổng bằng 1. Chứng minh

$\frac{1+a^2}{1+b^2}+\frac{1+b^2}{1+c^2}+\frac{1+c^2}{1+a^2}\leq \frac{7}{2}$

Không mất tính tổng quát, giả sử a=max{a,b,c}

Ta có: $\frac{1+a^2}{1+b^2}=\frac{(a^2+1)(b^2+1-b^2)}{b^2+1}=a^2+1-\frac{b^2(1+a^2)}{b^2+1}\leq a^2+1-\frac{b^2(1+a^2)}{2}$

Cmtt: $\frac{1+b^2}{1+c^2}\leq b^2+1-\frac{c^2(b^2+1)}{2};\frac{1+c^2}{1+a^2}\leq c^2+1-\frac{a^2(c^2+1)}{2}$

Cộng vế theo vế ta được: $\frac{1+a^2}{1+b^2}+\frac{1+b^2}{1+c^2}+\frac{1+c^2}{1+a^2}\leq 3+a^2+b^2+c^2-\frac{a^2(b^2+1)+b^2(c^2+1)+c^2(a^2+1)}{2}=\frac{a^2+b^2+c^2-(a^2b^2+b^2c^2+a^2c^2)}{2}+3\leq \frac{a^2+b^2+c^2+2(ab+bc+ac)}{2}+3=\frac{7}{2}$

Dấu ''='' xảy ra khi a=1; b=c=0

Bài 57: Cho $a,b,c>0$ và $ab+bc+ac=abc$. Chứng minh rằng $P=\frac{a^{4}+b^{4}}{ab(a^{3}+b^{3})}+\frac{b^{4}+c^{4}}{bc(c^{3}+b^{3})}+\frac{c^{4}+a^{4}}{ac(c^{3}+a^{3})}\geq 1$

Ta có:$ab+bc+ac= abc\Rightarrow \frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$

Ta có: $2(a^4+b^4)\geq (a^3+b^3)(a+b)\Rightarrow \frac{a^4+b^4}{a^3+b^3}\geq \frac{a+b}{2}\Rightarrow \frac{a^4+b^4}{ab(a^3+b^3)}\geq \frac{a+b}{2ab}$

CMTT: $\frac{b^4+c^4}{bc(b^3+c^3)}\geq \frac{b+c}{2bc}; \frac{a^4+c^4}{ac(a^3+c^3)}\geq \frac{a+c}{2ac}$

Cộng vế theo vế ta được: $\sum \frac{a^4+b^4}{ab(a^3+b^3)}\geq \frac{1}{2}(\sum \frac{a+b}{ab})\doteq \frac{1}{2}(2.\sum \frac{1}{a})=1$

Dấu ''='' xảy ra khi a=b=c=3

Bài 38:
IMG_20180418_224653.jpg
P/s: Xin lỗi m.n mình đang dùng đt nên không gõ Latex được

Mình xin đưa ra lời giải bài trên:

Áp dụng BĐT Holder ta có:

$(1+3)(1+3)(1+3)(a^4+3)\geq (a+3)^4\Rightarrow \sqrt[4]{a^4+3}\geq \frac{a+3}{\sqrt[4]{64}}$

Cmtt: $\sqrt[4]{b^4+3}\geq \frac{b+3}{\sqrt[4]{64}}; \sqrt[4]{c^4+3}\geq \frac{c+3}{\sqrt[4]{64}}$

Cộng vế theo vế ta được: $\sqrt[4]{a^4+3}+\sqrt[4]{b^4+3}+\sqrt[4]{c^4+3}\geq \frac{(a+b+c)+3+3+3}{\sqrt[4]{64}}$

Áp dụng BĐT AM-GM, có: $(a+b+c)+3+3+3\geq 4\sqrt[4]{27(a+b+c)}\Rightarrow \sum \sqrt[4]{a^4+3}\geq \frac{4\sqrt[4]{27(a+b+c)}}{\sqrt[4]{64}}=\sqrt[4]{108(a+b+c)}$

Bài 31: Cho $x,y,z$ thỏa mãn $13x+5y+12z=9$. Tìm giá trị lớn nhất của $A=\frac{xy}{2x+y}+\frac{3yz}{2y+z}+\frac{6zx}{2z+x}$

Bài 38:

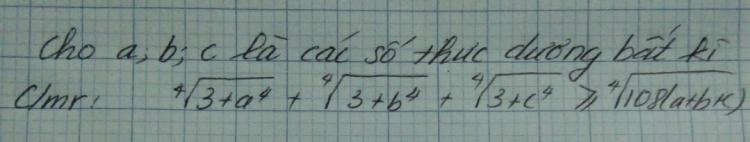
P/s: Xin lỗi m.n mình đang dùng đt nên không gõ Latex được

Bài 12: 
Cho các số thực dương a,b,c. Chứng minh:
$\frac{a}{b} + \frac{b}{c} + \frac{c}{a} \ge \frac{{a + b + c}}{{\sqrt[3]{{abc}}}}$ (Sưu tầm)

  (Sưu tầm Bđt của thầy Phạm Kim Hùng)

Ta nhóm và sử dụng BĐT AM-GM

$3(\frac{a}{b}+\frac{b}{c}+\frac{c}{a})=(\frac{2a}{b}+\frac{b}{c})+(\frac{2b}{c}+\frac{c}{a})+(\frac{2c}{a}+\frac{a}{b})\geq \frac{3a}{\sqrt[3]{abc}}+\frac{3b}{\sqrt[3]{abc}}+\frac{3c}{\sqrt[3]{abc}}\Rightarrow \frac{a}{b}+\frac{b}{c}+\frac{c}{a}\geq \frac{a+b+c}{\sqrt[3]{abc}}$

1. Tìm giá trị nhỏ nhất của hàm số $\frac{x}{1-x}+\frac{5}{x}$với 0<x<1

$\frac{x}{1-x}+\frac{5}{x}=\frac{x}{1-x}+\frac{5(1-x)+5x}{x}=\frac{x}{1-x}+\frac{5(1-x)}{x}+5\geq 2\sqrt{5}+5$

Dấu ''='' xảy ra khi $x=\frac{5-\sqrt{5}}{4}$

Bài 11: 

Cho các số thực dương a, b, c. Chứng minh:

$\frac{a}{{\sqrt {\left( {2{\rm{a}} + b} \right)\left( {2{\rm{a}} + c} \right)} }} + \frac{b}{{\sqrt {\left( {2b + a} \right)\left( {2b + c} \right)} }} + \frac{c}{{\sqrt {\left( {2c + a} \right)\left( {2c + b} \right)} }} \le 1$ (Nguyễn Việt Hùng)

P/s: các bạn hãy đưa ra các bài phù hợp với lớp 9 một chút

áp dụng BĐT Cauchy- Schwartz

Ta có: $(2a+b)(2a+c)=(a+a+b)(a+c+a)\geq (a+\sqrt{ac}+\sqrt{ab})^2=a(\sqrt{a}+\sqrt{b}+\sqrt{c})^2\Rightarrow \sqrt{(2a+b)(2a+c)}\geq \sqrt{a}.(\sqrt{a}+\sqrt{b}+\sqrt{c})\Rightarrow \frac{a}{\sqrt{(2a+b)(2a+c)}}\leq \frac{a}{\sqrt{a}.(\sqrt{a}+\sqrt{b}+\sqrt{c})}=\frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}$

Cmtt: $\frac{b}{\sqrt{(2b+a)(2b+c)}}\leq \frac{\sqrt{b}}{\sqrt{a}+\sqrt{b}+\sqrt{c}};\frac{c}{\sqrt{(2c+a)(2c+b)}}\leq \frac{\sqrt{c}}{\sqrt{a}+\sqrt{b}+\sqrt{c}}$

Cộng vế theo vế ta được đpcm

Dấu ''='' xảy ra khi a=b=c

Mk xin được làm bài này:
Ta có: $x^3+y^3+z^3=(x+y+z)^3-3(x+y)xy-3z(x+y)(x+y+z)=(x+y+z)^3-3xy(x+y+z)-3z(x+y)(x+y+z)-3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)-3xyz=(x+y+z)\frac{xyz}{2}-3xyz=\frac{xyz}{2}(x+y+z-6)$

P/s: Mk nghĩ bài toán phải chữa thành $x^3+y^3+z^3\vdots x+y+z-6$ mới đúng.
Bạn thử đưa ra một số liệu cụ thể thử xem sao!

Nếu x=1, y=2,z=3 thì 1+2+3-6=0 thì sai rồi bạn

Cho x,y,z là các số thực lớn hơn 1 và thỏa mãn điều kiện: xy+yz+xz+xyz=20. Chứng minh

$\frac{3}{x+y+z-3}\geq (x-1)(y-1)(z-1)$

Cho a,b,c là các số thực dương thỏa mãn điều kiện a+b+c=3

Chứng minh rằng: $\frac{4}{(a+b)^3}+\frac{4}{(c+b)^3}+\frac{4}{(a+c)^3}\geq \frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{b+a}$

Cho a,b,c là các số thực không âm có tổng bằng 1. Chứng minh

$\frac{1+a^2}{1+b^2}+\frac{1+b^2}{1+c^2}+\frac{1+c^2}{1+a^2}\leq \frac{7}{2}$