Mấy hôm nay ngồi chơi chơi với cái Geogebra thì đột nhiên nghĩ ra 1 bài toán khá lạ,đăng lên cho mọi người thảo luận:
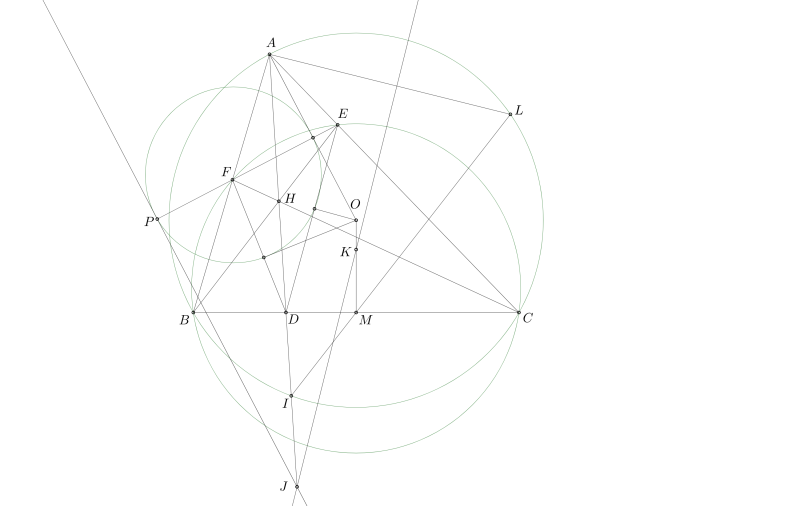
Bài toán:Cho $\Delta ABC$ nhọn,đường cao $BE,CF$,$M$ là trung điểm $BC$.Giả sử $(BME),(CMF)$ có giao điểm 2 tiếp tuyến chung ngoài là $K$ và $K$ nằm trên đường tròn ngoại tiếp $\Delta ABC$.Chứng minh $AK\perp BC$
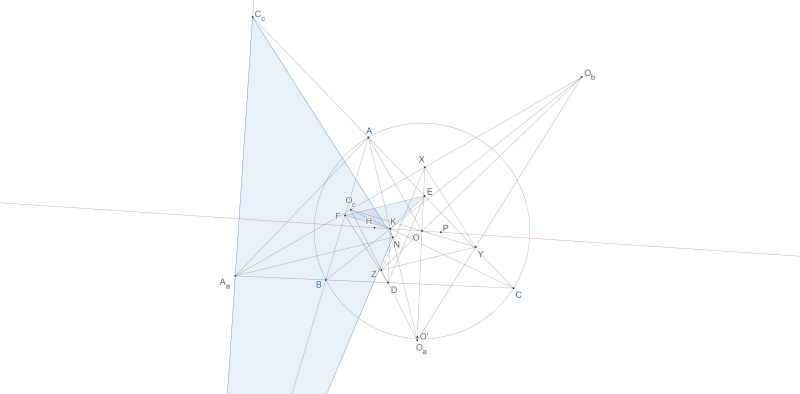
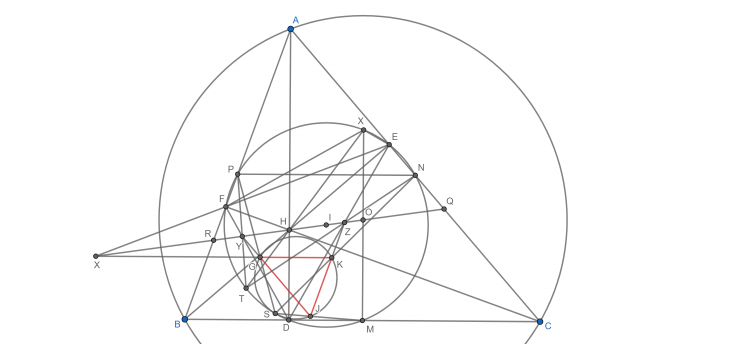
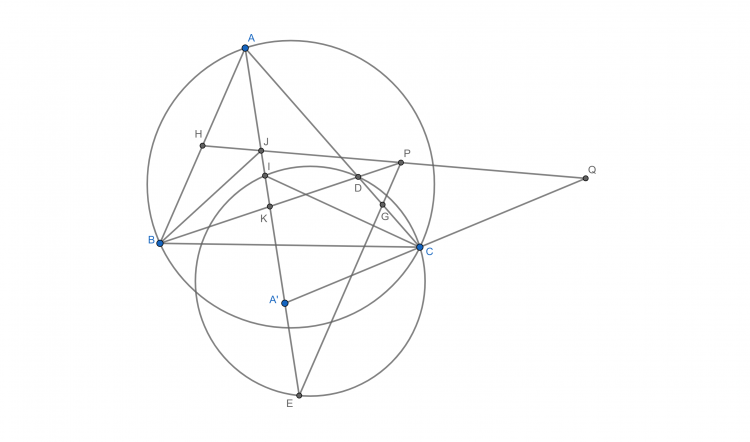
Chứng minh bài toán sau: Cho $\Delta ABC$ nội tiếp $(O), S$ là điểm chính giữa cung $BAC$ của $(O), M$ trung điểm $BC. K$ thuộc $(O)$ sao cho $AK \perp BC,$ đường cao $BE, CF.$ Giả sử $AK=SM,$ khi đó $K$ là tâm vị tự ngoài của $(BME)$ và $(CMF)$
Gợi ý: Kẻ đường kính $AA'.SM, A'M$ cắt $(O)$ tại $T, N,$ chứng minh $K$ là tâm $(NMT)$ để suy ra $K, O_1,O_2, S$ thẳng hàng, để ý $KC$ tiếp xúc $(CMF), KB$ tiếp xúc $(BME)$ là được
Sau đó áp dụng bài toán trên vào bài toán ban đầu sẽ có đpcm
- huytran08 yêu thích



 Tìm kiếm
Tìm kiếm Nam
Nam