huytran08

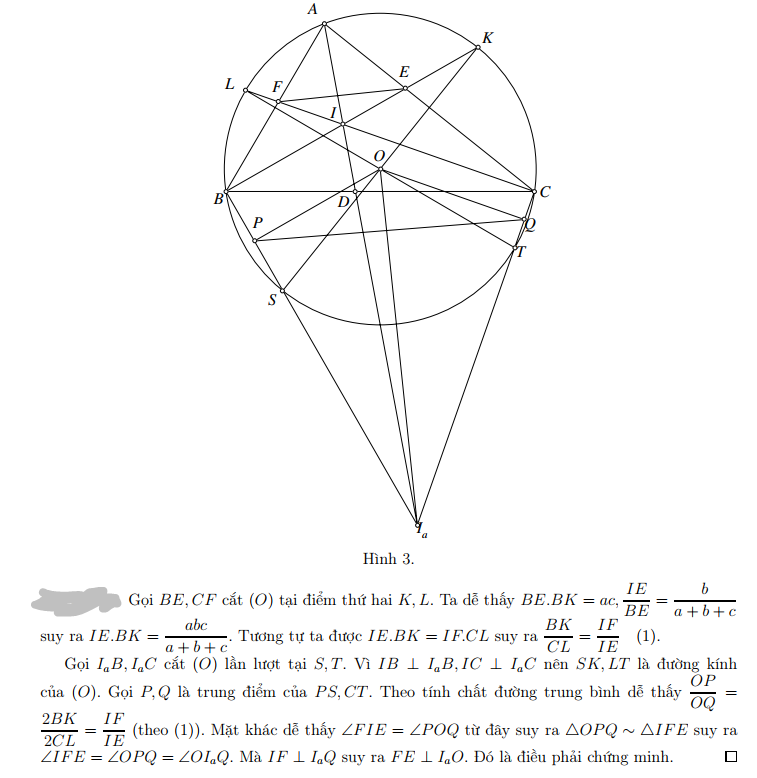
Gọi $X, Y, Z, T, U, V$ là trung điểm của $AD, BD, BC, AC, AB, DC$;$YZ$ cắt $UT$ tại $E$,$XT$ cắt $YV$ tại $F$; ta có $XYZT$ và $UYVT$ là các hình bình hành.

Vì $MNPQ$ là hình bình hành nên

 $I=MP\cap NQ\Leftrightarrow I$ là trung điểm của $MP$ và $NQ$

$\Leftrightarrow I$ thuộc miền chung của 2 hình bình hành $XYZT$ và $UYVT$ hay là hình bình hành $EYFT$

Vậy $I$ thuộc miền hình bình hành $EYFT$.

đây bạn

Tiếp tục với bài 3:

Bài toán 3. Cho $\Delta ABC$ nội tiếp $(O)$.Điểm $P$ nằm trong cung nhỏ $BC$ điểm $Q$ đối xứng $P$ qua $BC$ nằm trong $\Delta ABC$. $BQ,CQ$ cắt $AC, AB$ tại $E, F$.$PE$ cắt $(O)$ tại $X$. Chứng minh $BX$ chia đôi $EF$.

                                                                                                              Lời giải

Gọi $(ABE)$ cắt $BC$ tại $D$

Ta có:$ \widehat{EQF}=\widehat{BQC}=\widehat{BPC}=180^{o}-\widehat{BAC}\Rightarrow AEQF$ nội tiếp

         $ \Rightarrow \widehat{EQC}=\widehat{BAC}=\widehat{EDC}\Rightarrow EQDC$ nội tiếp

        $ \Rightarrow \widehat{BAD}=\widehat{BED}=\widehat{BCF}=\widehat{BCP}=\widehat{BAP}$

        $ \Rightarrow A,D,P$ thẳng hàng

Gọi $G$ đối xứng $P$ qua $D$ thì $GQ//BC$ nên $\widehat{DGQ}=\widehat{GDB}=\widehat{AEB}$

  suy ra $AEQG$ nội tiếp

Từ đó dễ có:$ \widehat{EGD}=\widehat{EFB}$ và $ \widehat{FBE}=\widehat{GDE}$

Vậy $\Delta EFB\sim \Delta EDG(g.g)$.

Gọi $I$ là trung điểm $EF$ thì $\Delta IFB\sim \Delta EGP(c.g.c)$ suy ra $\widehat{ABI}=\widehat{APE}=\widehat{ABX}$

  $\Rightarrow B,I,X$ thẳng hàng (đpcm)

Bạn có thể đưa ra lời giải hai câu sau không?

Có chứ bạn,mình giải tạm câu 2 trước nhé

Bài toán 2. Cho $\Delta ABC$ nội tiếp $(O)$. Đường tròn $(O')$ đi qua 2 điểm $B, C$ cắt $AC,AB$ tại $E, F$.$BE$ cắt $CF$ tại $H$.$AH$ cắt $(O)$ tại $P$. $PE$ cắt $(O)$ tại $X$. Chứng minh $BX$ chia đôi $EF$.

                                                                                                    Lời giải

Gọi $(FBH)$ cắt $AP$ tại $M$

Ta có:$AH.AM=AF.AB=AE.AC$ nên $EHMC$ nội tiếp

   $\Rightarrow \widehat{BMC}=360^{o}-(\widehat{BMN}+\widehat{CMN})=(180^{o}-\widehat{BMN})+(180^{o}-\widehat{CMN})$

                                                                  $=\widehat{BFC}+\widehat{BEC}=\widehat{BO'C}$

   $ \Rightarrow BMO'C$ nội tiếp $\Rightarrow \widehat{O'MC}=\widehat{O'BC}=\frac{180^{o}-\widehat{BO'C}}{2}$

Xét:$\widehat{AMO'}=\widehat{CMN}-\widehat{O'MC}=180^{o}-\frac{\widehat{BO'C}}{2}-\frac{180^{o}-\widehat{BO'C}}{2}=90^{o} \Rightarrow O'M\perp AP $

Gọi $N$ đối xứng $P$ qua $M$,$J$ đối xứng $F$ qua $O'M$ thì $J \in (O')$ và $FNPJ$ là hình thang cân

Có:$ \widehat{FJC}=\widehat{ABC}=\widehat{APC}$ nên $C,P,J$ thẳng hàng

 Gọi $AP$ cắt $BC$ tại $L$

 $\widehat{ANP}=\widehat{FJC}=\widehat{ABC} \Rightarrow BFNL$ nội tiếp

 Tương tự có $CENL$ nội tiếp suy ra $AENF$ nội tiếp

  $\Rightarrow \widehat{ENP}=180^{o}-\widehat{ANE}=180^{o}-\widehat{AFE}=\widehat{BFE}$

Mặt khác ta có $\widehat{EMN}=\widehat{ACF}=\widehat{ABE}$ nên $\Delta EMN\sim \Delta EBF(g.g) \Rightarrow \frac{MN}{BF}=\frac{EN}{EF}=\frac{NP}{2BF} $

  Gọi $I$ là trung điểm $EF$ thì $\frac{NP}{2BF}=\frac{EN}{2IF} \Rightarrow \frac{NP}{BF}=\frac{EN}{IF}$

  $\Rightarrow \Delta ENP\sim \Delta IFB\Rightarrow \widehat{ABI}=\widehat{APE}=\widehat{ABX}$

  $\Rightarrow B,I,X$ thẳng hàng(đpcm)

Bài đây

Gọi $IC$ cắt $AB$ tại $F$.

Dễ thấy $E(FD,IC)=-1$ mà $IM//EF$ do cùng vuông góc với $OI_{a}$ nên $DE$ đi qua trung điểm $IM$

Bài này trước em có giải,đổi $t$ thành $w$ là được

Đặt $f(x)=2x^{3}-x^{2}+x-1;g(x)=4x^{3}-2x^{2}+x-1$

Giả sử $f(x)$ có ít nhất 2 nghiệm thực $a\neq c$

Khi đó:$f(a)-f(c)=0$ 

           $\Leftrightarrow (2a^{3}-a^{2}+a-1)-(2c^{3}-c^{2}+c-1)=0$

           $\Leftrightarrow 2(a^{3}-c^{3})-(a-c)(a+c)+a-c=0$ 

           $\Leftrightarrow (a-c)\left [ (a+c)^{2}+\left ( a-\frac{1}{2} \right )^{2} +\left ( c-\frac{1}{2} \right )^{2}+\frac{1}{2}\right ]=0$

           $\Leftrightarrow a=c$ (vô lí)

 Tương tự ta có $g(x)$ có 1nghiệm thực duy nhất là $b$

Dễ chứng minh $a,b\neq 0$

Xét:$g(\frac{1}{2a})=4\left ( \frac{1}{2a} \right )^{3}-2\left ( \frac{1}{2a} \right )^{2}+\frac{1}{2a}-1=\frac{1}{2a^{3}}-\frac{1}{2a^{2}}+\frac{1}{2a}-1$

                                                                           $=\frac{1-a+a^{2}-2a^{3}}{2a^{3}}=\frac{-f(a)}{2a^{3}}=0=g(b)$

     $ \Rightarrow \frac{1}{2a}=b\Rightarrow ab=\frac{1}{2}$

 

 

 

Câu 3. (3.0 điểm) Cho $a, b, c$ là các số thực dương thỏa mãn $2abc=2a+4b+7c$

Tìm giá trị nhỏ nhất của biểu thức $P =a+b+c$.

 

 

 

Ta có: $c=\dfrac{2a+4b}{2ab-7}$ nên $P = a + b + \frac{2a+4b}{2ab-7}$.

Áp dụng bất đẳng thức AM-GM, ta có:

$$ P = a + \dfrac{{11}}{{2a}} + \left( {b - \dfrac{7}{{2a}}} \right) + \left( {\dfrac{{2a + 4b}}{{2ab - 7}} - \dfrac{2}{a}} \right) $$
$$ \Leftrightarrow P = a + \dfrac{{11}}{{2a}} + \dfrac{{2ab - 7}}{{2a}} + \dfrac{{2{a^2} + 7}}{{2ab - 7}} $$
$$ \Leftrightarrow P \geqslant a + \dfrac{{11}}{{2a}} + \dfrac{{2\sqrt {{a^2} + 7} }}{a} $$
Đến đây đã dồn biểu thức về 1 biến và có thể giải bằng nhiều cách 
Đáp án: $ {P_{\min }} = \dfrac{{15}}{2} \Leftrightarrow a= 3,b = \dfrac{5}{2},c = 2 $

1,Cho $G$ là đồ thị trên tập hợp $V$ gồm $2n$ đỉnh và có $m\geq n^{2}+1$ cạnh.

 Giả sử $G$ không chứa tam giác.Khi đó các cạnh kề nhau không có đỉnh kề chung,do đó $d(x)+d(y) \leq 2n$ với mọi cạnh {$x,y$}$\in E$.

Cộng theo tất cả các cạnh của $G$ ta có:$\sum _{x\in V}d(x)^{2}=\sum _{{x,y}\in E}(d(x)+d(y))\leq 2mn $

Mặt khác theo BĐT $Cauchy-Schwarz$ và đẳng thức $Euler \sum _{x\in V}d(x)=2m$ ta có:

$\sum _{x\in V}d(x)^{2} \geq \frac{\left ( \sum_{x\in V}d(x) \right )^{2}}{\left | V \right |}=\frac{2m^{2}}{n} $

Từ đó suy ra $m\leq n^{2}$,mâu thuẫn

$Q.E.D$

Kẻ đường cao $AD,BE$ của $\Delta ABC$

Dễ thấy các tứ giác $DHNM$ và $DHEC$ nội tiếp nên $AN.AM=AH.AD=AE.AC$ suy ra $MNEC$ nội tiếp

  $\Rightarrow \widehat{MNC}=\widehat{MEC}=\widehat{MCA}$ nên $\Delta MNC\sim \Delta MCA(g.g)$

Từ đó ta có: $\frac{NC}{AC}=\frac{MN}{MC}=\frac{MN}{MB}=\frac{NB}{AB}\Rightarrow \frac{NB}{NC}=\frac{AB}{AC}$

Đồng thời $\widehat{BNC}=\widehat{BNM}+\widehat{MNC}=\widehat{ABC}+\widehat{ACB}=180^{o}-\widehat{BAC}$ nên nếu ta gọi $S$ đối xứng $N$ qua $BC$ thì $ABSC$ nội tiếp và $\frac{SB}{SC}=\frac{NB}{NC}=\frac{AB}{AC}$ suy ra $ABSC$ là tứ giác điều hoà

 $\Rightarrow KA=KS=KN$(đpcm)

Mở rộng:Kẻ $KN$ cắt $AB,AC$ tại $P,Q$;$R$ là tâm $(APQ)$.Chứng minh $(PQR)$ tiếp xúc $(O)$

"Tìm GTLN của $P=a+ab+abc$ biết $a,b,c$ là các số thực không âm thoả mãn $a+b+c=3$" đúng không bạn?

Nếu đúng thì bạn xem tại đây.

Cho $a,b,c$ là các số thực dương.Chứng minh rằng:

     $\sum \frac{2\sqrt{2}+c^{2}\sqrt{2}+\sum \frac{\sqrt{a^{8}+b^{8}}}{c^{2}}}{(\sum a)\left [ 3\sqrt{(3abc+P-Q)(\sum a)} \right ]^{\frac{1}{2}}+2(a+b)(1-c)-(c^{2}-1)}\geq 2\sqrt{2}$

 Với $P=\sum \frac{b}{\left [ a^{2}+\sqrt{\frac{\sqrt[4]{2}}{2\sqrt{2}}(\sum a^{2}\sqrt{a^{4}+b^{4}}+\sum b^{2}\sqrt{a^{4}+b^{4}})(\sum a)} \right ]^{\frac{1}{2}}}$

       $Q=\sum \frac{b}{\left [ a^{2}+\sqrt{3abc(\sum \sqrt{a\sqrt{bc}})} \right ]^{\frac{1}{2}}}$

Đặt $x=\frac{1}{a};y=\frac{1}{b};z=\frac{1}{c}$ thì $x,y,z>0$ và $xyz=1$.

Khi đó:$\sum \sqrt[4]{2a^{2}+bc}=\sum \sqrt[4]{\frac{2}{x^{2}}+\frac{1}{yz}}=\sum \sqrt[4]{\frac{x^{2}+2yz}{x}}$

BĐT cần chứng minh trở thành: 

            $ \sum \sqrt[4]{\frac{x^{2}+2yz}{x}}\leq \frac{x+y+z}{\sqrt[4]{3}}\sqrt{\frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}}}$

Hay:$\left ( \sum \sqrt[4]{\frac{x^{2}+2yz}{x}} \right )^{4}\leq \frac{(x+y+z)^{4}}{3}.\left ( \frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}} \right )^{2} $

Áp dụng BĐT $Holder$ ta có:

    $3(x^{2}+2yz+y^{2}+2xz+z^{2}+2xy) \left ( \frac{1}{\sqrt{x}}+\frac{1}{\sqrt{y}}+\frac{1}{\sqrt{z}} \right )^{2}\geq \left ( \sum \sqrt[4]{\frac{x^{2}+2yz}{x}} \right )^{4}$

 Như vậy ta chỉ cần chứng minh:$\frac{(x+y+z)^{4}}{3}\geq 3(x^{2}+2yz+y^{2}+2xz+z^{2}+2xy) $

                                                    $\Leftrightarrow x+y+z\geq 3$ (luôn đúng)

                                   $\Rightarrow \sum \sqrt[4]{2a^{2}+bc}\leq \frac{ab+bc+ca}{\sqrt[4]{3}}\sqrt{\sqrt{a}+\sqrt{b}+\sqrt{c}}$

 Dấu "=" xảy ra $\Leftrightarrow  a=b=c=1$ (thoả mãn)

Kẻ đường cao $BI,CJ$ của $\Delta ABC$;$KD,KE$ cắt $BH,CH$ tại $P,Q$

Do $DE\perp HN$ nên $DE$ là phân giác $\widehat{BHJ}$ và $\widehat{CHI}$ 

Từ đó có $\widehat{ADE}=\widehat{BHD}+\widehat{ABH}=\widehat{CHE}+\widehat{ACH}=\widehat{AED}$ nên $\Delta ADE$ cân tại $A$ suy ra $KD\perp AB$ và $KE\perp AC$

    $\Rightarrow \frac{HP}{BP}=\frac{DJ}{BD}=\frac{HJ}{HB}=\frac{HI}{HC}=\frac{IE}{EC}=\frac{HQ}{QC}$

 Nên $PQ//BC$ suy ra $HM$ đi qua trung điểm $F$ của $PQ$

 Mặt khác dễ chứng minh $HPKQ$ là hình bình hành nên $HK$ đi qua $F$

  Từ đó suy ra $H,K,M$ thẳng hàng(đpcm).