HaiDangPham

Chúng ta tiếp tục với Nhóm 5, chặng cuối cùng. Bài 12 b) tương đối khó, thiết nghĩ cũng không nên trì hoãn lâu hơn. Hi vọng chúng ta có thể hoàn thành trọn vẹn chuyên đề trong Tháng 5 này! Mời mọi người tham gia! 

 

NHÓM 5 (Năm 2021, 2022, 2023) 

 

BÀI 13. (Năm 2021) 

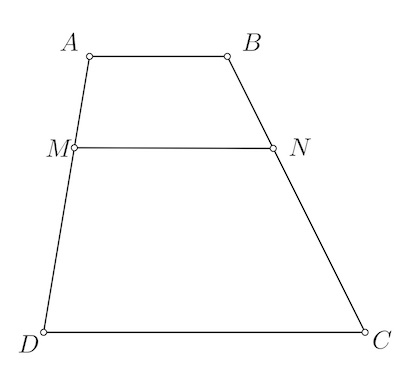
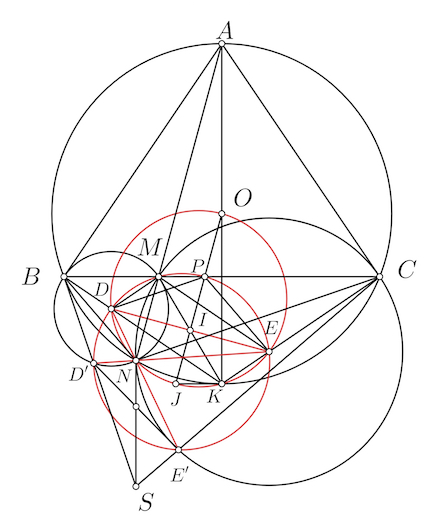
Cho đường tròn $(O; R)$. Dây cung $BC$ cố định không đi qua tâm $O$. Trên tia đối của tia $BC$ lấy điểm $A$ ($A$ khác $B$). Từ $A$ kẻ hai tiếp tuyến $AM$ và $AN$ tới đường tròn $(O)$ ($M$ và $N$ là hai tiếp điểm). Gọi $I, H$ lần lượt là trung điểm của $BC$ và $MN$;  $BC$ cắt $MN$ tại $K$.

            a) Chứng minh bốn điểm $O, M, N, I$ cùng thuộc một đường tròn và $HK$ là tia phân giác của góc $BHC$.

            b) Hai tiếp tuyến của đường tròn $(O)$ tại $B$ và $C$ cắt nhau ở $E$. Chứng minh $M, N, E$ thẳng hàng.

            c) Đường thẳng $\Delta$ qua điểm $M$ và vuông góc với $ON$, cắt đường tròn $(O)$ tại điểm thứ hai là $P$. Xác định vị trí của điểm $A$ trên tia đối của tia $BC$ để tứ giác $AMPN$ là hình bình hành.

 

BÀI 14. (Năm 2022) 

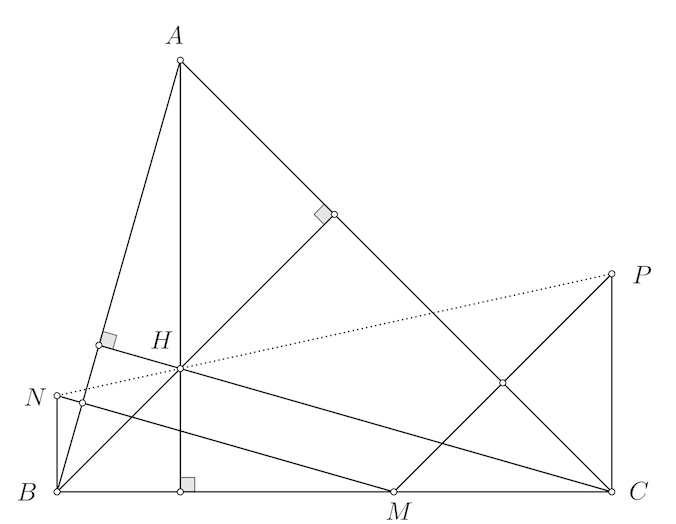
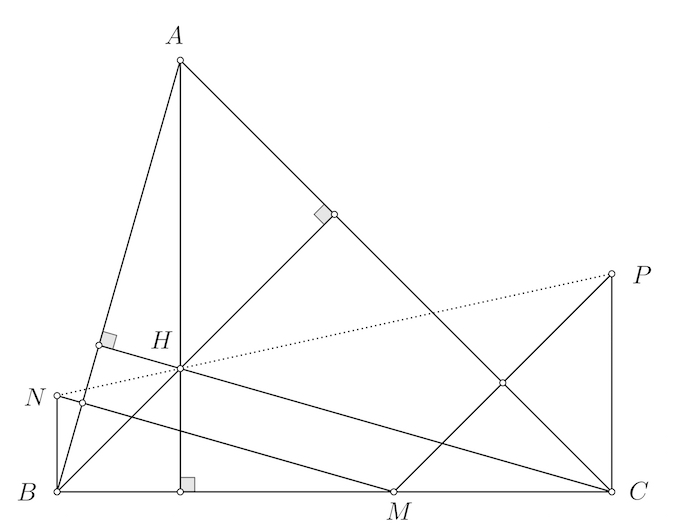
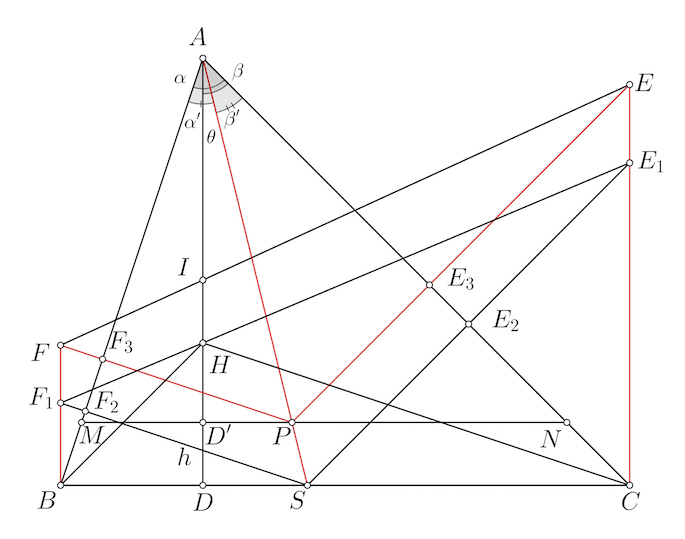
Cho tam giác $ABC$ là tam giác nhọn, không cân, $AB<AC$, nội tiếp đường tròn tâm $O$. Gọi $M, N, P$ lần lượt là trung điểm của các cạnh $BC, CA, AB$. Đường thẳng $PO$ cắt đường thẳng $AM$ tại $D$, đường thẳng $NO$ cắt đường thẳng $AM$ tại $E$, đường thẳng $BD$ cắt đường thẳng $CE$ tại $F$.

            a) Chứng minh bốn điểm $B, C, O, F$ cùng thuộc một đường tròn.

            b) Chứng minh tam giác $FEO$ đồng dạng với tam giác $NEM$.

            c) Chứng minh rằng $\angle OPF=\angle ONF$.

 

BÀI 15. (Năm 2023) 

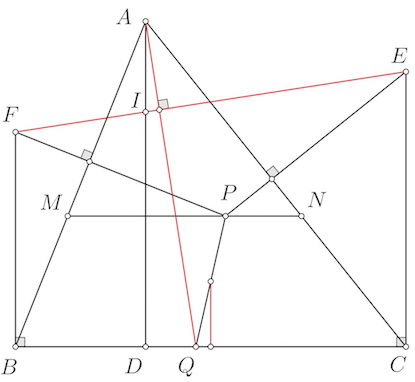
Cho 3 điểm phân biệt cố định $A, B, C$ cùng năm trên đường thẳng $d$ (điểm $B$ nằm giữa $A$ và $C$), gọi $I$ là trung điểm của đoạn thẳng $BC$. Đường tròn tâm $O$ luôn đi qua hai điểm $B$ và $C$ (điểm $O$ không thuộc $d$). Kẻ tiếp tuyến $AM, AN$ với đường tròn tâm $O$ ($M, N$ là các tiếp điểm). Đường thẳng $MN$ cắt $OA$ tại điểm $H$ và cắt $BC$ tại điểm $K$.

            a) Chứng minh tứ giác $OMNI$ nội tiếp và $AH.OA=AN^2$.

            b) Khi đường tròn tâm $O$ thay đổi, chứng minh $MN$ luôn đi qua điểm $K$ cố định.

            c) Tia $AO$ cắt đường tròn $O$ tại hai điểm $P, Q$ (điểm $P$ nằm giữa $A$ và $O$). Gọi $D$ là trung điểm của $HQ$. Từ $H$ kẻ đường thẳng vuông góc với $MD$ và cắt đường thẳng $MP$ tại $E$. Chứng minh $P$ là trung điểm $ME$.

 

$sin\widehat{AMC}$ là anh dùng tỉ số lượng giác trong tam giác nhọn ạ?

 

Chỗ đó $\sin 135^{\circ}=\sin 45^{\circ}=\frac{1}{\sqrt{2}}$. Nói chung bài này là để thi vào 10 thì hơi khó. Giải như cách trên của mình thật sự không hay. Nhưng thôi, tạm vậy đã. 

Hiện tại mình chỉ nghĩ ra cách này thôi. Chắc sẽ có cách khác dùng hình phụ. 

 

Đặt $AM=x, CM=y$.

Xét tứ giác nội tiếp $AMCB$ có

(i) $AB=2R$,

(ii) $AC=BC=\sqrt{2}R$ và

(iiI) $BM=\sqrt{4R^2-x^2}$. 

Áp dụng Định lý Ptoleme ta có 

$AM.BC+MC.AB=BM.AC$

$\Leftrightarrow x.\sqrt{2}R+y.2R=\sqrt{4R^2-x^2}.\sqrt{2}R$

$\Leftrightarrow x+\sqrt{2}y=\sqrt{4R^2-x^2}$ (chia cả hai vế cho $\sqrt{2}R$) 

$\Leftrightarrow x^2 +2y^2 +2\sqrt{2}xy=4R^2-x^2$ (bình phương cả hai vế) 

$\Leftrightarrow x^2+y^2+\sqrt{2}xy=2R^2$. 

Ta có $2xy \leq x^2+y^2 $, suy ra $2xy+\sqrt{2}xy \leq x^2+y^2+\sqrt{2}xy=2R^2$.

Vậy

$xy \leq (2-\sqrt{2})R^2 $. 

 

Tiếp theo, gọi $r$ là bán kính đường tròn nội tiếp tam giác $AMC$. Khi đó $S_{AMC}=\frac{1}{2}.(MA+MC+AC).r=\frac{1}{2}.(x+y+\sqrt{2}R).r$. 

Lưu ý rằng $\angle AMC=135^{\circ}$ nên $S_{AMC}=\frac{1}{2}.\sin{\angle AMC}.MA.MC. =\frac{1}{2}.\frac{1}{\sqrt{2}}.xy=\frac{\sqrt{2}}{4}xy$. 

Do đó $\frac{\sqrt{2}}{4}xy=\frac{1}{2}.(x+y+\sqrt{2}R).r$. Vậy 

$\boxed{\frac{1}{r}=\sqrt{2}.\frac{x+y+\sqrt{2}R}{xy}}$. 

Ta có $\frac{x+y}{xy} \geq \frac{2}{\sqrt{xy}} \geq \frac{2}{\sqrt{2-\sqrt{2}}R}=\frac{\sqrt{4+2\sqrt{2}}}{R}$  và $\frac{\sqrt{2}R}{xy} \geq \frac{\sqrt{2}R}{(2-\sqrt{2})R^2}=\frac{\sqrt{2}+1}{R}$.  

Vì vậy $\frac{1}{r} \geq \frac{\alpha}{R}$ hay $r \leq \frac{R}{\alpha}$, trong đó $\alpha=\sqrt{2}.(\sqrt{4+2\sqrt{2}}+\sqrt{2}+1)$. 

Dấu "=" xảy ra khi $x=y$. 

Vậy bán kính đường tròn nội tiếp tam giác $AMC$ đạt giá trị lớn nhất khi $M$ nằm chính giữa cung $AC$. 

 

_____

Có thể chứng minh $x^2+y^2+\sqrt{2}xy=2R^2$ nhanh hơn bằng cách dùng Định lý hàm cos $AC^2=MA^2+MC^2-2MA.MC.\cos \angle AMC$. 

Quocminh nên đăng toàn bộ bài toán thì hay hơn. Dữ kiện cho $I$ và $K$, chẳng liên quan gì tới yêu cầu cần giải quyết cả. Chắc là lại tách câu cuối ra thì phải. 

Lời giải của kograysus chính xác ạ! 

 

Mình có một hướng tiếp cận khác. Không mấy khó khăn ta chứng minh được hai cặp tam giác đồng dạng sau: 

(1) Tam giác $MDH$ và tam giác $ADC$

(2) Tam giác $MDE$ và tam giác $ADH$. 

Từ đây ta suy ra $\frac{ME}{AH}=\frac{MH}{AC} \left( =\frac{MD}{AD} \right) $, hay $\frac{ME}{MH}=\frac{AH}{AC}$.

Vì $H$ là trung điểm của $AC$ nên từ đẳng thức trên ta suy ra $E$ là trung điểm của $MH$. 

 

Các bước suy luận trên đây có thể phát biểu lại thành một Bổ đề: 

 

 Cho tam giác $ABC$ và tam giác $A'B'C'$ đồng dạng. Hai điểm $M$ và $M'$ tương ứng nằm trên hai cạnh $BC$ và $B'C'$. Khi đó $\frac{MB}{BC}=\frac{M'B'}{B'C'}$ khi và chỉ khi tam giác $MAB$ đồng dạng với tam giác $M'A'B'$.

 

Phát biểu thành một bổ đề, để nhấn mạnh rằng có không ít các bài toán mà mình từng làm đã vận dụng nó. Ban đầu mình cũng chẳng để ý tới sự tồn tại của nó nhưng sau do gặp cũng nhiều nên coi nó gần như một kiểu định lý về hai tam giác đồng dạng để vận dụng vậy! 

 

Chẳng hạn, gần đây nhất có bài toán sau (đây chính là Bổ đề 3 mình dùng để chứng minh Bài 12 trong topic 15 bài toán hình từ kỳ thi học sinh giỏi tỉnh Ninh Bình): 

 

Bài toán 2. Cho tam giác $ABC$ có $H$ là trực tâm. Gọi $M$ là một điểm nằm trên cạnh $BC$. Lấy hai điểm $N, P$ sao cho $NM \perp AB$, và $NB \perp BC$; $PM \perp AC$ và $PC \perp BC$. Khi đó ba điểm $H, N, P$ thẳng hàng. 

 

Có thời gian mình sẽ tổng hợp thêm một số bài toán nữa.

Bài sau đây chỉ là ý cuối bài thi vào 10, không quá khó, nhưng cần sử dụng tới một bài toán (bổ đề) theo mình nghĩ là khá cơ bản và hay. 

 

Bài toán. Cho đường tròn $(O)$ đường kính $AB$. $M$ là một điểm nằm trên tiếp tuyến tại $A$ của đường tròn.  Từ $M$ kẻ tiếp tuyến $MC$ tới đường tròn ($C$ là tiếp điểm). Gọi $D$ là giao điểm thứ hai của $MB$ và đường tròn, $H$ là giao điểm $MO$ và $AC$.  Chứng minh $CD$ đi qua trung điểm của $MH$. 

Thầy @thvn nói về các bài toán "căn bản" trong hình học THCS làm mình nhớ ngày xưa có vài bài thú vị cho lớp 6,7

 

1) Cho tam giác $ABC$ nhọn. Trên $BC$ lấy $D, E$ sao cho $\angle BAD = \angle DAE = \angle EAC$. Trong 3 đoạn thẳng $BD,DE,EC$, đoạn nào dài nhất?

 

 

Mấy bài kiểu này rất thú vị! Sau đây mình giải phần 1). 

a) Xét trường hợp tam giác $ABC$ có hai cạnh $AB, AC$ độ dài khác nhau. Không mất tính tổng quát giả sử $AB < AC$. Ta sẽ chứng minh $EC$ có độ dài lớn hơn $BD$ và $ED$. 

 

* Chứng minh $BD<EC$. 

Theo quan hệ giữa góc và cạnh đối diện trong tam giác, vì $AB<AC$ nên $\angle C<\angle B$. 

Ta có $\angle ADE$ là góc ngoài tam giác $ADB$, còn $\angle AED$ là góc ngoài tam giác $AEC$. Hơn nữa $\angle BAD=\angle CEA$ và $\angle C<\angle B$. Do đó $\angle AED<\angle ADE$. Vì vậy $AD<AE$. 

 

Tiếp theo, gọi $D_1, D_2$ lần lượt là chân đường vuông góc hạ từ $D$ xuống $AB, AE$; $E_1, E_2$ lần lượt là chân đường vuông góc hạ từ $E$ xuống $AC, AD$. 

 

Do $AD$ là tia phân giác của góc $BAE$, $AE$ là tia phân giác của góc $DAC$ nên ta có ngay $DD_1=DD_2$ và $EE_1=EE_2$. 

 

Ta có $DD_2.AE=EE_2.AD=2S_{ADE}$. Mà $AD<AE$ nên $DD_2<EE_2$ hay $DD_1<EE_1$. 

 

Ta lại có $AB<AC$ nên $AB.DD_1<AC.EE_1$ hay $S_{ABD}<S_{AEC}$. 

 

Mà $\frac{BD}{EC}=\frac{S_{ABD}}{S_{AEC}}$. Chứng tỏ $BD<EC$. 

 

*Chứng minh $ED<EC$. 

Ta có $\angle ADC>\angle B>\angle C$. Do đó $AC>AD$. Mà $\frac{ED}{EC}=\frac{AD}{AC}$ ($AE$ là tia phân giác của góc $CAD$). Chứng tỏ $ED < EC$. 

 

b) Trường hợp $AB=AC$, khi đó tam giác $ABD$ bằng tam giác $ACE$ (g.c.g), suy ra $BD=EC$. Chứng minh tương tự như trường hợp a) ta có $ED<BD=EC$. 

 

____

Chứng minh trên không cần tới giả thiết tam giác $ABC$ nhọn. Liệu có bị thiếu sót ở đâu không? 

Trong vai trò một ĐHV, mình có chút góp ý là bạn huytran08 nên đặt lại tiêu đề topic này như bình thường, tức là nội dung cần chứng minh thuộc về bài toán gốc.

 

Tiêu đề "Xuất phát từ một bài toán hình cơ bản" có lẽ sẽ không đúng với quy định. Nó chung chung, không xác định vấn đề cụ thể là gì. 

 

Cứ lấy tiêu đề với bài toán gốc, người đọc khi vào xem sẽ tự biết bạn muốn đề cập tới các bài toán mở rộng ạ! 

Tuần vừa rồi mình bận khá nhiều việc riêng nên giờ mới viết bài tiếp theo được. 

 

Trong bài này chúng ta sẽ vẽ Đường tròn Euler (Đường tròn 9 điểm) của tam giác ABC cho trước. Kỹ năng quan trọng nhất là học hai cách vẽ đường tròn: (i) Vẽ đường tròn với tâm và bán kính cho trước. (ii) Vẽ đường tròn đi qua 3 điểm cho trước. 

 

Bài học cũng yêu cầu các bạn phải xử lý nhiều đối tượng hơn. Bước cuối cùng tuỳ chỉnh thuộc tính của điểm và đường khá mất công, nhưng các bạn hãy cứ kiên trì để làm cho quen! Các công cụ cơ bản thì mất thời gian hơn những vẫn rất cần thiết. Nó giống như việc ta học đạp xe trước khi biết đi xe máy vậy! 

 

Các bạn có thể tải ngay Bài 4 tại đây. 

 

Bài toán trên, như đã nói là một bài thi học sinh giỏi của THPT. Mình vẫn giữ nó ở topic này, vì dù sao đó cũng là một bài toán hay. Sau khi tìm được đúng đề thi THCS mình sẽ bổ sung sau.

 

Bài viết sau sẽ chứng minh phần a).

 

Về kiến thức, cần phải sử dụng tới hai công thức biến đổi lượng giác của chương trình lớp 10 là 

(i) $\cos (x \pm y)=\cos x \cos y \mp \sin x \sin y$

(ii)  $ \sin (x \pm y)=\sin x \cos y \pm \cos x \sin y$.  

 

Trong phần chính của chứng minh ta cần 3 bổ đề sau:

 

Cho hình thang $ABCD$ có $AB$ và $CD$ song song với nhau và cùng vuông góc $AD$ ($AB<CD$). Gọi $\alpha$ là góc tạo bởi $AD$ và $BC$. Khi đó $BC= \frac{AD}{\cos \alpha}$.

Cho hình thang $ABCD$ ($AB \parallel CD$). Hai điểm $M$ và $N$ tương ứng thuộc $AD$ và $BC$ sao cho $MN$ song song với hai đáy của hình thang. Khi đó $MN=\frac{MD}{AD}.AB+\frac{MA}{AD}.CD$.

Cho tam giác $ABC$ có $H$ là trực tâm. Gọi $M$ là một điểm nằm trên cạnh $BC$. Lấy hai điểm $N, P$ sao cho $NM \perp AB$, và $NB \perp BC$; $PM \perp AC$ và $PC \perp BC$. Khi đó ba điểm $H, N, P$ thẳng hàng.

Ba bổ đề trên đây bạn đọc có thể tự chứng minh không mấy khó khăn. Theorem và Theorem, phục vụ cho mục đích tính toán. Theorem quan trọng hơn cả. Theo mình, bổ đề này dường như chính là bài toán gốc mà từ đó người ta đã phát triển lên thành bài toán trong đề thi.

 

_______

Bây giờ, với ba bổ đề trên ta quay trở lại bài toán.

 

Gọi $H$ là trực tâm tam giác $ABC$, $D’$ là giao điểm $AD$ và $MN$, $S$ là giao điểm $AP$ và $BC$. 

Qua $S$ ta kẻ đường thẳng vuông góc với $AC$ cắt $CE$, $AC$ lần lượt tại $E_1, E_2$; kẻ đường thẳng vuông góc với $AB$ cắt $BF, AB$ lần lượt tại $F_1$ và $F_2$.

$E_3$ là giao điểm $PE$ và $AC$, $F_3$ là giao điểm $PF$ và $AB$.

 

Tiếp theo ta đặt $DD’=h$ và $\angle BAD=\alpha, \angle CAD=\beta, \angle SAB=\alpha’, \angle SAC=\beta’$. Ta có $\alpha+\beta=\alpha’+\beta’$.

Không mất tính tổng  quát ta giả sử $P$ thuộc đoạn $D’N$ và đặt $\theta=\alpha’-\alpha=\beta-\beta’$.

 

Để chứng minh $I$ cố định, ta chứng minh $IH=h$ không đổi.

 

Thật vậy, trước hết áp dụng công thức tính diện tích tam giác theo hàm sin ta có

 

$\frac{BD}{BC}=\frac{S_{ABD}}{S_{ABC}}=\frac{AB.AD.\sin \alpha}{AB.AC.\sin (\alpha+\beta)}=\frac{AD}{AC}.\frac{\sin \alpha}{\sin (\alpha+\beta)} = \frac{\cos \beta.\sin \alpha}{\sin (\alpha+\beta)} $.

Chứng minh tương tự ta có $\frac{CD}{BC}=\frac{\cos \alpha.\sin \beta}{\sin (\alpha+\beta)} $.

 

Áp dụng Theorem cho hình thang vuông $E_2E_3EE_1$ và hình thang vuông $E_2E_3PS$ ta có $EE_1=\frac{E_2E_3}{\cos \beta}$ và $E_2E_3=\cos \beta'.PS$.

Do đó $EE_1=\frac{\cos \beta’}{\cos \beta}.PS$. Tương tự $FF_1=\frac{\cos \alpha’}{\cos \alpha}.PS$.

 

Áp dụng Theorem cho hình thang vuông $DD’PS$ ta có $PS=\frac{DD’}{\cos \theta}=\frac{h}{\cos \theta}$.

 

Theo Theorem ta có $E_1, H, F_1$ thẳng hàng. Xét hình thang $EFF_1E_1$ có $I, H$ tương ứng thuộc hai cạnh $EF, E_1F_1$ và $IH$ song song với hai đáy, áp dụng Theorem ta có

$IH=\frac{F_1H}{E_1F_1}. EE_1+ \frac{E_1H}{E_1F_1}.FF_1$

$= \frac{BD}{BC}.EE_1+ \frac{CD}{BC}. FF_1$

$=\frac{\cos \beta.\sin \alpha}{\sin (\alpha+\beta)}. \frac{\cos \beta’}{\cos \beta}.PS+\frac{\cos \alpha.\sin \beta}{\sin (\alpha+\beta)}.\frac{ \cos \alpha’}{\cos \alpha}.PS.$

$=\frac{\sin \alpha.\cos \beta’+\sin \beta.\cos \alpha’}{\sin (\alpha+\beta)}. PS.$

$=\frac{\sin \alpha.\cos \beta’+\sin \beta.\cos \alpha’}{\sin (\alpha+\beta).\cos \theta}. h$.

 

Cuối cùng, do $\theta=\alpha’-\alpha=\beta-\beta’$ nên $\alpha’=\alpha+\theta$ và $\beta’=\beta-\theta$. Từ đó ta có

$\sin \alpha.\cos \beta’+\sin \beta.\cos \alpha’$

$=\sin \alpha. \cos (\beta-\theta)  + \sin \beta. \cos (\alpha+\theta)$

$= \sin \alpha. (\cos \beta.\cos \theta+\sin \beta.\sin \theta)+\sin \beta. (\cos \alpha \cos \theta-\sin \alpha.\sin \theta)$

$= (\sin \alpha.\cos \beta+\cos \alpha.\sin \beta).\cos \theta$

$= \sin (\alpha+\beta).\cos \theta$.

 

Chứng tỏ $IH=h$, không đổi. Vậy $I$ cố định.

 

______

Bàn luận thêm:  

 

1) Mình đã hoàn toàn không nghĩ tới việc xét trường hợp đặc biệt khi $MN$ trùng với $BC$ ngay từ đầu mà quanh quẩn với việc tạo ra các điểm phụ vô cùng phức tạp. Chỉ tới sáng nay, quay trở lại với bài toán, trực giác tự nhiên nói với mình rằng cần phải xét trực tâm tam giác $ABC$. Không rõ tại sao, nhưng mình vẫn thử và rồi ý tưởng dần hiện ra. Với điểm phụ $H$ việc biến đổi lượng giác để tính $IH$ trở nên hoàn toàn khả thi.

 

2) Để mọi người hiểu hơn tại sao mình lại nhìn ra $IH=DD’$ thì cần phải quay trở lại với các hình phụ mà mình đã phát triển trong quá trình tìm tòi vất vả trước đó.

 

Nếu ta gọi $M’$ là giao điểm của $MN$ và $BF$, thì ta có một dự đoán rằng $IM’ \parallel BH$ (và cùng vuông góc với $AC$). Điều này tương đương với $IH=BM’$ ($IM’BH$ là hình bình hành) và có nghĩa $IH=DD’$.

 

3) Nói thêm, với cách vẽ hình phụ như trên, $I$ chính là trực tâm của tam giác $M’AN$. Dường như chính từ đây mà mình nghĩ tới việc tạo thêm điểm phụ $H$ là trực tâm của tam giác ABC chăng? Không rõ nữa, trực giác đôi khi vận hành theo cách khó mà lý giải rõ ràng ra được.

 

Sự tư duy  của chúng ta xảy ra ở một nơi rất sâu, còn cái ý nghĩ mà ta thấy được nơi trí óc chỉ là cái phóng chiếu bề nổi của tiến trình tư duy đó.

Đặt $y=\sqrt{2x+1}$. Khi đó $x=\frac{y^2-1}{2}$. Thay vào phương trình ban đầu và biến đổi ta có phương trình ẩn $y$ là 

$$ y^6-9y^4 +8y^3-9y^2+1=0. $$ 

Phương trình trên có dạng đối xứng, thế nên ta chia cả hai vế phương trình cho $y^3$, nhóm các hạng tử và ta  được phương trình mới là 

$$ \left ( y^3+\frac{1}{y^3} \right )-9\left ( y+\frac{1}{y}\right )+8=0.$$

Đặt $z=y+\frac{1}{y}$. Khi đó $y^3+\frac{1}{y^3}=z^3-3z$. Ta có phương trình bậc ba ẩn $z$ dạng suy biến 

$$ z^3-12z+8=0. $$

Tới đây ta giải ra được $z$, rồi tìm lại được $y$ và cuối cùng là $x$. Do công thức nghiệm khá phức tạp nên mình xin được bỏ qua bước làm này. 

_____

 

Mình đã có ý tưởng về phương trình ẩn $y$ ngay từ đầu, nhưng lại không thể nào nhìn ra đó là phương trình dạng đối xứng! Thấy bậc 6 chán quá rồi nên bỏ cuộc luôn. Làm đi làm lại nhiều cách không thành rồi tự nhiên phát hiện ra điểm mấu chốt đó! 

 

Bài này mình nghĩ là có thể giải bằng lượng giác. 

Mọi người lưu ý Bài 12 là bài chọn đội tuyển học sinh giỏi THPT năm 2020 của tỉnh Ninh Bình chứ không phải THCS!

 

Do trong đề không ghi rõ khối lớp, mà mình lại chỉ để ý vào bài hình nên không phát hiện ra sai sót này trong quá trình tổng hợp đề! 

 

Đường link dẫn tới toàn bộ đề ở đây. 

 

Mình cũng chưa tìm kiếm được đề năm 2020 của Ninh Bình nên chúng ta tạm bỏ qua bài này. Tuy nhiên mình vẫn sẽ để nó ở đây (cho tới lúc tìm được đề thay thế), nếu bạn nào muốn giải nó thì hãy thử sử dụng các kiến thức của THPT ạ. Với kiến thức của THCS mình thấy thật sự bế tắc. 

 

Cảm ơn Leonguyen vì phát hiện ra sai sót này của mình! 

 

Rất xin lỗi mọi người vì sự thiếu cẩn thận này! 

Mời mọi người tiếp tục với các bài toán NHÓM 4 ạ! 

 

NHÓM 4. (Ba năm 2018, 2019, 2020) 

 

 

BÀI 12. (Năm 2020)  Cho tam giác nhọn $ABC$, đường cao $AD$ ($D$ thuộc $BC$) và hai điểm $M, N$ lần lượt nằm trên các cạnh $AB, AC$ sao cho $MN$ song song $BC$. Điểm $P$ chuyển động trên đoạn thẳng $MN$. Lấy các điểm $E, F$ sao cho $EP$ vuông góc $AC$, $EC$ vuông góc $BC$, $FP$ vuông góc $AB$, $FB$ vuông góc $BC$.

a) Gọi $I$ là giao điểm $EF$ và $AD$. Chứng minh rằng $I$ cố định khi $P$ chuyển động trên đoạn $MN$.

b) Đường thẳng qua $A$ vuông góc $EF$ cắt $BC$ tại $Q$. Chứng minh rằng đường trung trực của đoạn thẳng $BC$ đi qua trung điểm của đoạn thẳng $PQ$.

 

Bài 12 khá khó. Mình chưa có ý tưởng nào khả quan cả. Mọi người chung sức giải ạ! 

Bài 11. (mở rộng-dự đoán) 

e) Gọi $D'$, $E'$ lần lượt là giao điểm của đường tròn ngoại tiếp tứ giác $DMPE$ với đường tròn $(D)$ và đường tròn $(E)$. Hai đường thẳng $BD'$ và $CE'$ cắt nhau tại $S$. Chứng minh $N$ là trực tâm tam giác $SBC$ và $NS$ đi qua trung điểm của $D'E'$. 

 

$NS$ đi qua trung điểm của $D'E'$ là một dự đoán sai nhé mọi người! Cho điểm $M$ tiến sát vào điểm $B$ sẽ thấy ngay điều này không đúng! 

 

Mình bổ sung thêm câu sau các bạn có thể thử sức. 

 

 f) Tứ giác $D'NE'S$ là tứ giác nội tiếp. Gọi $T$ là giao điểm của $MN$ và đường tròn ngoại tiếp tứ giác $DMPE$ khi đó: 

(i) $T$ là tâm đường tròn ngoại tiếp tứ giác $D'NE'S$ (đã được chứng minh) 

(ii) Tam giác $TDE$ đồng dạng với tam giác $SBC$ (dự đoán) 

(iii) $N$ là trực tâm tam giác $TDE$. (dự đoán) 

 

Chúng ta kết thúc Bài 11 tại đây! 

Bài 11. (mở rộng-dự đoán) 

e) Gọi $D'$, $E'$ lần lượt là giao điểm của đường tròn ngoại tiếp tứ giác $DMPE$ với đường tròn $(D)$ và đường tròn $(E)$. Hai đường thẳng $BD'$ và $CE'$ cắt nhau tại $S$. Chứng minh $N$ là trực tâm tam giác $SBC$ và $NS$ đi qua trung điểm của $D'E'$. 

 

Sau đây là chứng minh cho phần đầu của câu e). 

Trước hết, ta có 

(1) $M$ và $N$đối xứng nhau qua $DE$. 

Điều này đúng vì $DM=DN$ (bán kính đường tròn $(D)$ và $EM=EN$ (bán kính đường tròn $(E)$). 

 

Tiếp theo ta có 

(2) $D, N, E'$thẳng hàng và $E, N, D'$thẳng hàng. 

Thật vậy, do tứ giác $DMEE'$ nội tiếp đường tròn và $EM=EE'$ (bán kính đường tròn $(E)$) nên $DE$ là tia phân giác của góc $MDE'$. Mà $DE$ cũng là tia phân giác của góc $MDN$ (vì $M$ và $N$ đối xứng nhau qua $DE$). Do đó $D, N, E'$ thẳng hàng. 

Chứng minh tương tự ta có $E, N, D'$ thẳng hàng. 

 

Bây giờ, ta thấy 

$ \angle CBS= \angle MBD'= \angle MNE$ (do $BMND'$ là tứ giác nội tiếp và $E, N, D'$ thẳng hàng) 

Mặt khác

$ \angle BCN= \angle BKN= \angle DKN= \angle DEN$( do $BCKN$ và $DEKN$ là hai tứ giác nội tiếp và $B, D, K$ thẳng hàng). 

Và hơn nữa

$ \angle MNE+ \angle DEN=90^{\circ}$ (vì $M$ và $N$ đối xứng nhau qua $E$). 

Do đó

$\angle CBS+\angle BCN=90^{\circ}$.

Tức là ta có $CN \perp BS$. 

Chứng minh tương tự ta có $BN \perp CS$. 

Vậy $N$ là trực tâm tam giác $BCS$.