neverstop

Công thức loại nào cũng được, vì hiện giờ tham vọng biểu diễn số nguyên tố dưới các công thức sơ cấp gần như không tưởng, các công thức "cao cấp" thì người ta nghiên cứu nhưng cũng đã có đâu. Như toanhoc nói ở trên, chỉ nói nguyên về vấn đề phân bố số nguyên tố cũng là bài toán rất lớn rồi, còn tiến đến biểu diễn các số nguyên tố thì còn bước dài nữa.

Định lí Lebnitz: (vo thanh van)

Định lí này nói về quan hệ độ dài trong liên hệ tâm tỉ cự. Định lí được áp dụng rất nhiều trong các bài toán về chứng minh, tính toán các khoảng cách giữa các điểm đặc biệt trong tam giác.

Định lí: Cho tam giác ABC. G là tâm tỉ cự của các điểm A, B, C theo các hệ số a, b, c tương ứng. Khi đó ta có: $aMA^2+bMB^2+cMC^2=(a+b+c)MG^2+aGA^2+bGB^2+cGC^2$ với mọi điểm M bất kì.

Định lí này có thể mở rộng cho n điểm như sau:
Định lí: Cho n điểm bất kì $A_1, A_2, ..., A_n$. G là tâm tỉ cự của các điểm đó theo các hệ số $a_1, a_2, ..., a_n$ tương ứng. Khi đó ta có: $a_1MA_1^2+a_2MA_2^2+...+a_nMA_n^2 = (a_1+a_2+...+a_n)MG^2+a_1GA_1^2+a_2GA_2^2+...+a_nGA_n^2$ với mọi điểm M bất kì.

Định lí trên cho ta hệ quả trực tiếp là tổng $a_1MA_1^2+a_2MA_2^2+...+a_nMA_n^2$ sẽ đạt cực trị (cực tiểu hoặc cực đại) khi M trùng với G.

Định lí Breichneider: (vo thanh van)

Định lí này còn được gọi là định lí hàm số cos cho tứ giác.

Định lí: Cho tứ giác ABCD. Gọi a, b, c, d, m, n lần lượt là độ dài các đoạn thẳng AB, BC, CD, DA, AC, BD. Khi đó: $m^{2}n^{2}=a^{2}c^{2}+b^{2}d^{2}-2abcd.cos(A+C)$

Rất cám ơn vo thanh van vì những ý kiến quý giá, dạo này anh ko lên mạng được nhiều nên chưa kịp bổ xung cho các định lí đã gửi. Anh sẽ cố gắng làm trong thời gian ngắn nhất.

Phần về tứ giác toàn phần em có thể nói rõ hơn được ko? 3 tam giác của tứ giác toàn phần là những tam giác nào vậy?

Các định lí em bổ xung đều khá hay, đều là những kết quả rất hay được sử dụng. Nói thật là bây giờ anh mới biết tên của nó đấy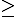 . Riêng định lí cuối cùng HELLY anh thấy có vẻ thuộc về hình học tổ hợp hơn nên có lẽ chưa đưa vào vội.

Cám ơn em đã đóng góp ý kiến.

@mods: những bài viết góp ý và trả lời của các thành viên và mods ko nên xóa, sẽ rất lộn xộn trong topic, hơn nữa để mọi người biết rõ hơn cách làm việc của chúng ta.

Bạn tìm đọc cuốn "Hình học phẳng" của Praxolov - bản dịch của nhà xuất bản Hải Phòng. Trong này trình bày từ những điều cơ bản đến những kết quả thông dụng, rất tốt để tìm hiểu về phép nghịch đảo.

Định lí Pappus

Định lý: Trên đường thẳng $d_1$lần lượt lấy các điểm$A_1,B_1,C_1$ Trên đường thẳng $d_2$ lần lượt lấy các điểm $A_2,B_2,C_2$. Gọi $A_3,B_3,C_3$ lần lượt là giao điểm của các cặp đường thẳng $B_1C_2$ và $B_2C_1$, $C_1A_2$ và $C_2A_1$, $A_1B_2$và $A_2B_1$. Khi đó $A_3,B_3,C_3$ thẳng hàng.

Chứng minh:(PDatK40SP)


Áp dụng phép chiếu xuyên tâm $ A_1 $
$ ( B_1DA_3A_2) = (OC_2B_2A_2) $
Áp dụng phép chiếu xuyên tâm $ C_1 $
$(B_1C_2C_3E) = (OC_2B_2A_2) $
$ \Rightarrow ( B_1DA_3A_2) =(B_1C_2C_3E) $
Xét phép chiếu tâm $ B_3 $ ta có điều phải chứng minh

zaizai: định lí trên còn có thể chứng minh dễ hiểu hơn bằng thuần túy hình học. Qua năm mới mình sẽ cố gắng post lên hoặc nhờ anh neverstop bổ sung. Cảm ơn PDatK40SP đã bổ sung 1 chứng minh hay.

Định lí Pascal

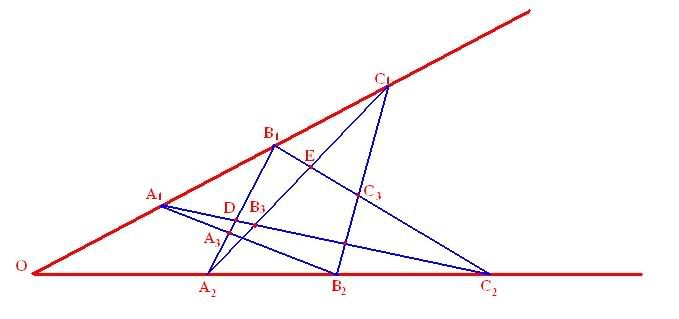
Định lý: Cho lục giác ABCDEF nội tiếp. Khi đó các giao điểm của các cặp cạnh đối AB và DE, BC và EF, CD và FA đồng quy.

Định lí Brianchon

Định lý này được coi là tương đương đối với định lý Pascal nhờ vào khái niệm Cực và đối cực (xem thêm tại đây)

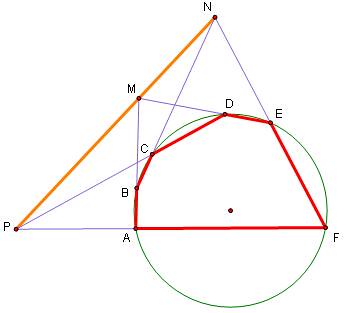
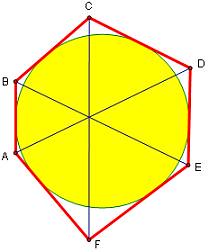
Định lý: Cho lục giác ABCDEF ngoại tiếp đường tròn (O). Khi đó các đường chéo lớn AD, BE, CF đồng quy.

Định lí Miquel

Định lý: Cho tam giác ABC. Các điểm D, E, F nằm trên các đường thẳng chứa các cạnh BC, CA, AB tương ứng. Khi đó các đường tròn ngoại tiếp các tam giác AEF, BFD, CDE đồng quy.



Chứng minh: Gọi I là giao điểm của hai đường tròn ngoại tiếp các tam giác BDF,CDE. Ta chứng minh I nằm trên đường tròn ngoại tiếp tam giác [AEF bằng góc định hướng. Thật vậy,
ABC, đường tròn qua D tiếp xúc với AB tại B, đường tròn qua D tiếp xúc với AC tại C đồng quy tại một điểm.

Khái niệm tam giác hình chiếu (zaizai)

Khái niệm này còn được gọi là tam giác bàn đạp và thuật ngữ tiếng Anh tướng ứng với nó là pedal triangle.

Định nghĩa: Cho tam giác ABC và điểm P bất kỳ. Từ P hạ đường vuông góc xuống các cạnh BC, CA, AB theo thứ tự cắt các cạnh đó tại D, E, F. Tam giác DFE gọi là tam giác hình chiếu của điểm P đối với tam giác ABC.



Tính chất (manutd): $S[DEF]=\dfrac{1}{4}(1-\dfrac{OP^2}{R^2}).S[ABC]$
trong đó ký hiệu S[XYZ] dùng để chỉ diện tích đại số (diện tích có hướng) của tam giác XYZ.

Khái niệm cực trực giao

Khái niệm này có tên tiếng Anh tương ứng là orthopole.

Định nghĩa: Cho tam giác ABC và một đường thẳng d bất kỳ. Từ các đỉnh A, B, C hạ các đường vuông góc xuống d cắt d tại M, N, P tương ứng. Từ M, N, P lần lượt hạ các đường vuông góc xuống các cạnh BC, CA, AB của tam giác ABC. Các đường vuông góc này đồng quy tại một điểm S gọi là cực trực giao của đường thẳng d đối với tam giác ABC.



Chứng minh: Gọi G,O,H lần lượt là hình chiếu của M,N,P lên BC,CA,AB (hình vẽ). Để chứng minh MG,NO,PH đồng quy ta dùng định lí Carnot, cụ thể là cần chứng minh:
$?GB^2-GC^2+OC^2-OA^2+HA^2-HB^2=0$
$\leftrightarrow MB^2-MC^2+NC^2-NA^2+PA^2-PB^2=0$
$\leftrightarrow MB^2-PB^2+NC^2-MC^2+PA^2-NA^2=0$
$\leftrightarrow MN^2-PN^2+NP^2-MP^2+PM^2-NM^2=0$
Đẳng thức cuối hiển nhiên đúng, ta có ĐPCM.

Khái niệm điểm đẳng giác

Khái niệm này còn có tên gọi hơi khác là điểm đẳng giác liên hợp, khái niệm tiếng Anh tương ứng là isogonal conjugate.

Định nghĩa: Cho tam giác $ABC$ và một điểm $M$ bất kỳ. Các đường thẳng đối xứng của $AM, BM, CM$ tương ứng qua các đường phân giác góc $A, B, C$ sẽ đồng quy tại 1 điểm $M'$. Điểm $M'$ này được gọi là điểm đẳng giác của điểm $M$.

Chú ý:điểm đẳng giác của trọng tâm tam giác được gọi là điểm đối trung. Điểm này có tên tiếng Anh là symmedian point. Các đường thẳng đối xứng với các trung tuyến của tam giác qua các đường phân giác tương ứng được gọi là các đường đối trung, tên tiếng Anh của chúng tương ứng cũng là symmedian line.

Tính chât 1: Nếu điểm $M $là tâm tỉ cự của bộ 3 điểm $A, B, C$ theo các hệ số $x, y, z$ thì $M'$ là tâm tỉ cự của bộ ba điểm $A, B, C$ theo các hệ số $\dfrac{a^2}{x}, \dfrac{b^2}{y}, \dfrac{c^2}{z}$, trong đó $a, b, c$ là độ dài các cạnh của tam giác $ABC$.

Tính chất 2: Gọi $D,E,F$ thứ tự là hình chiếu của $M$ lên $BC,CA,AB$, $D',E',F'$ thứ tự là hình chiếu của $M'$ lên $BC,CA,AB$. Ta có 6 điểm $D,E,F,D',E',F'$ nằm trên một đường tròn, tâm $O$ của đường tròn này là trung điểm $MM'$. Ngoài ra ta cũng chứng minh được $AM'\perp EF,BM'\perp FD,CM'\perp DE$.
(tính chất này được chứng minh trực tiếp từ định nghĩa, bạn đọc tự chứng minh)

Định lí Carno (manutd)

Định lý: Cho tam giác ABC và các điểm M, N, P lần lượt thuộc các đường thẳng BC, CA, AB. Gọi x, y, z lần lượt là đường thẳng vuông góc với BC, CA, AB tại M, N, P tương ứng. Khi đó x, y, z đồng quy khi và chỉ khi đẳng thức sau thỏa mãn:
$MB^2-MC^2+NC^2-NA^2+PA^2-PB^2=0$.



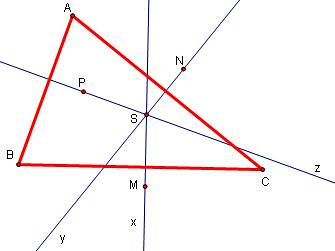
Chứng minh:

Gọi X, Y, Z là các giao điểm của x, y, z với BC, CA, AB tương ứng.

Phần thuận:
Giả sử x, y, z, đồng quy tại 1 điểm S, ta cần chứng minh hệ thức trên được thỏa mãn.

Theo định lý Pythagores ta có: $MB^2-MC^2+NC^2-NA^2+PA^2-PB^2=(XB^2+XM^2)-(XC^2+XM^2)+(YC^2+YN^2)-(YA^2+YN^2)+(ZA^2+ZP^2)-(ZB^2+ZP^2)$
$XB^2-XC^2+YC^2-YA^2+ZA^2-ZB^2=(XB^2+XS^2)-(XC^2+XS^2)+(YC^2+YS^2)-(YA^2+YS^2)+(ZA^2+ZS^2)-(ZB^2+ZS^2)$
$XB^2-XC^2+YC^2-YA^2+Z'A^2-Z'B^2=0$
Từ đó suy ra $Z'A^2-Z'B^2 = ZA^2-ZB^2$.
Mặt khác ta thấy $ZA^2-ZB^2 = (\bar{ZA}+\bar{ZB})(\bar{ZA}-\bar{ZB})=2\bar{ZD}.\bar{BA}$ với D là trung điểm của AB.
Tương tự ta có $Z'A^2-Z'B^2 = 2\bar{Z'D}.\bar{BA}$
Từ đây suy ra $2\bar{ZD}.\bar{BA} = 2\bar{Z'D}.\bar{BA}$.
suy ra Z trùng với Z', tức x, y, z đồng quy.

Định lí Desargues

Định lý này là 1 kết quả cơ bản của hình học xạ ảnh về 2 tam giác thấu xạ. Tuy nhiên cách chứng minh của nó lại chỉ đơn thuần dùng hình học sơ cấp cho nên được ứng dụng khá nhiều..

Định lý: Cho tam giác ABC và tam giác A'B'C'. Khi đó điều kiện cần và đủ để các đường thẳng nối các đỉnh tương ứng của 2 tam giác đồng quy là các giao điểm của các cạnh tương ứng của 2 tam giác thẳng hàng; tức AA', BB', CC' đồng quy khi và chỉ khi các giao điểm của BC và B'C', CA và C'A', AB và A'B' thẳng hàng.



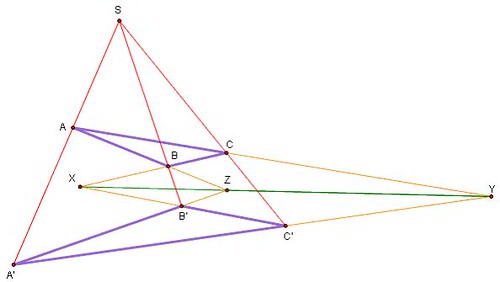
Chứng minh:

Gọi X, Y, Z là các giao điểm các cặp cạnh BC và B’C’, CA và C’A’, AB và A’B’ tương ứng.

Phần thuận:
Giả sử các đường thẳng AA’, BB’, CC’ đồng quy tại S. Ta chứng minh X, Y, Z thẳng hàng.
Áp dụng định lí Mê-nê-la-uyt cho tam giác SB’C’ với cát tuyến XBC ta có:
$\dfrac{\bar{XB}}{\bar{XB}}.\dfrac{\bar{C'C}}{\bar{C'S}}.\dfrac{\bar{B'S}}{\bar{B'B}}=1$ hay $\dfrac{\bar{XB}}{\bar{XB}} = \dfrac{\bar{SC'}}{\bar{SB'}}.\dfrac{\bar{BB'}}{\bar{CC'}}$

Tương tự, ta có:
$\dfrac{\bar{YC}}{\bar{YA}} = \dfrac{\bar{SA'}}{\bar{SC'}}.\dfrac{\bar{CC'}}{\bar{AA'}}$ và $\dfrac{\bar{ZA}}{\bar{ZB}} = \dfrac{\bar{SB'}}{\bar{SA'}}.\dfrac{\bar{AA'}}{\bar{BB'}}$

Nhân từng vế các đẳng thức trên lại với nhau, và theo định lí Mê-nê-la-uyt suy ra X, Y, Z thẳng hàng.

Phần đảo:
Giả sử các điểm X, Y, Z thẳng hàng. Ta chứng minh các đường thẳng AA’, BB’, CC’ đồng quy.
Gọi S là giao điểm của AA’ và BB’. SC cắt đường thẳng AC’ tại C”.
Xét 2 tam giác ABC và A’B’C” có các đường nối các đỉnh tương ứng đồng quy, do đó theo phần thuận giao điểm của các cạnh tương ứng cũng đồng quy.
Ta thấy AB cắt A’B’ tại Z, AC cắt A’C” tại Y (do A’, C’, C” thẳng hàng), suy ra giao điểm X’ của BC và B’C” phải thuộc YZ. Tức là X’ là giao của YZ và BC nên X’ trùng với X.
Suy ra C” trùng với C’, hay AA’, BB’, CC’ đồng quy.

Mình thấy trong diễn đàn, phần Hình học Olympic có rất nhiều câu hỏi cơ bản như: điểm đẳng giác là gì, đường đối trung là như thế nào, cực trực giao là sao, ... hay những thuật ngữ trên nhưng viết bằng tiếng Anh như thế nào, những khái niệm tiếng Anh thì ở tiếng Việt cái gì là tương đương, ...

Những kiến thức này trong chương trình phổ thông không được dạy. Thường thì các bạn sẽ tìm được chúng trong các tài liệu tham khảo nâng cao, hoặc từ trên mạng, hoặc được bồi dưỡng, truyền thụ lại.

Mình thiết nghĩ những kiến thức này rất cần thiết và cơ bản cho bất kỳ một học sinh nào muốn bước chân vào khu vực Olympic. Nói vậy có nghĩa là các bạn nên chuẩn bị những kiến thức cơ bản thật vững trước khi đánh trận nơi đây. Những sự giúp đỡ, giải đáp của người khác sẽ không thể đáp ứng được toàn bộ những câu hỏi cơ bản như vậy.

Cho nên mình muốn lập ra topc này để mọi người gửi những thắc mắc, những câu hỏi về một khái niệm, tính chất cơ bản nào đó của một vấn đề hình học mở rộng (tức không có trong chương trình phổ thông) để tập hợp những lời giải đáp vào chung một nơi tiện cho các bạn tra cứu.

Tất cả những câu hỏi và câu trả lời sẽ được cập nhật tại trang này. Mong các bạn thường xuyên để ý. Những kết quả nêu ở mục này xin được phép không nêu chứng minh ở trang đầu tiên, để cho gọn gàng và dễ tra cứu. Tuy nhiên trong các bài viết tiếp theo, nếu bạn nào có thể chứng minh, xin góp sức chung.

Nếu trong quá trình biên soạn các định nghĩa và tính chất, có điều gì chưa chính xác hoặc thiếu, rất mong các bạn góp ý.

--------------------------------------------------------------------------------------------------

I. Mục lục các khái niệm

1. Khái niệm điểm đẳng giác

2. Khái niệm cực trực giao

3. Khái niệm tam giác hình chiếu

4. Khái niệm tứ giác toàn phần


II. Mục lục các định lý

1. Định lí Miquel

2. Định lí Carno

3. Định lí Desargues

4. Định lí Pascal

5. Định lí Brianchon

6. Định lí Pappus

7. Định lí Thebault

8. Định lí Breichneider

9. Định lí Lebnitz