Ronaldo

R khả ly chứ . Lấy tập Q .

Đề bài không chuẩn . Chọn L^p là đủ .

Bài toán này chỉ nên dành cho học sinh lớp 12 thôi 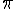. Thời phổ thông mình gặp nhiều bài dạng này rồi .

Bất đẳng thức chắc đúng đấy . Xin lỗi vì chưa nghĩ kỹ lắm .

Chứng minh bằng cách quy nạp theo $n $

Chứng minh hàm $x^p + (a-x)^p$ ($p>1$) là tăng nếu $x\geq\dfrac{a}{2}$

Nhờ kết hàm này, ta có thể biến đổi sao cho $x_1 = y_1$ ở đây $\{x_i\}$ và $\{y_i\}$ được sắp xếp giảm dần (cho nó dễ xử lý )

Anh nghĩ là chú chả chịu nghĩ gì cả

Thôi được, nếu gợi ý vậy mà vẫn chưa nghĩ ra, thì mình sẽ làm hộ vậy .

Chọn $\{\dfrac{1}{n}: n\in\mathbb{N}\}\cup\{0\}$ là tập compact

Đặt $\epsilon_n= \dfrac{1}{n-1}-\dfrac{1}{n}$

Với mỗi $n$ đặt $x^n_k = \dfrac{1}{n} + \dfrac{1}{2^k}\epsilon_n$

Khi đó
$\dfrac{1}{n}<x^n_k\leq \dfrac{1}{2}\left(\dfrac{1}{n}+\dfrac{1}{n-1}\right)$

từ đó thấy các dãy này rời nhau rồi .

Xét tập $A= \{\dfrac{1}{n}: n\in\mathbb{N}\}\cup\{0\} \cup\{x^n_k\}$
Tập điểm giới hạn chính là tập

$\{\dfrac{1}{n}: n\in\mathbb{N}\}\cup\{0\}$ .

Tập điểm giới hạn của tập mình xây dựng ở trên là
$\{\dfrac{1}{n} : n\in N\}\cup\{0\}$ , thế là đếm được rồi chứ