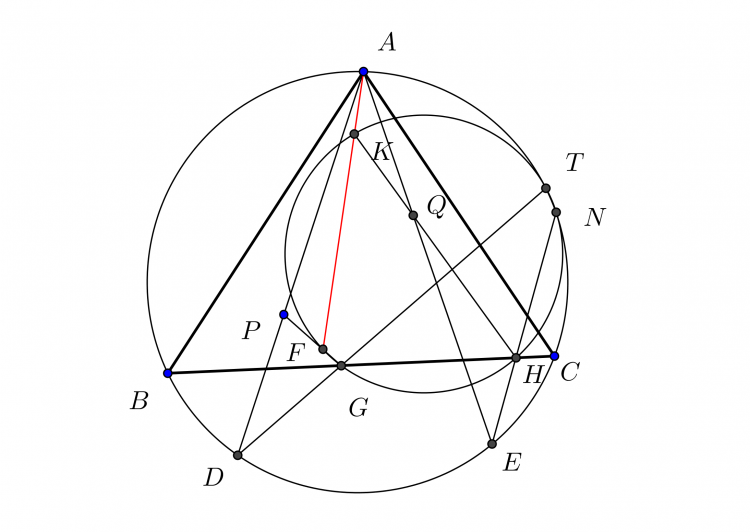
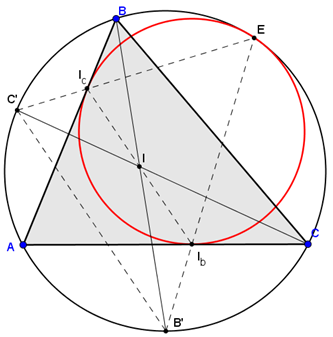
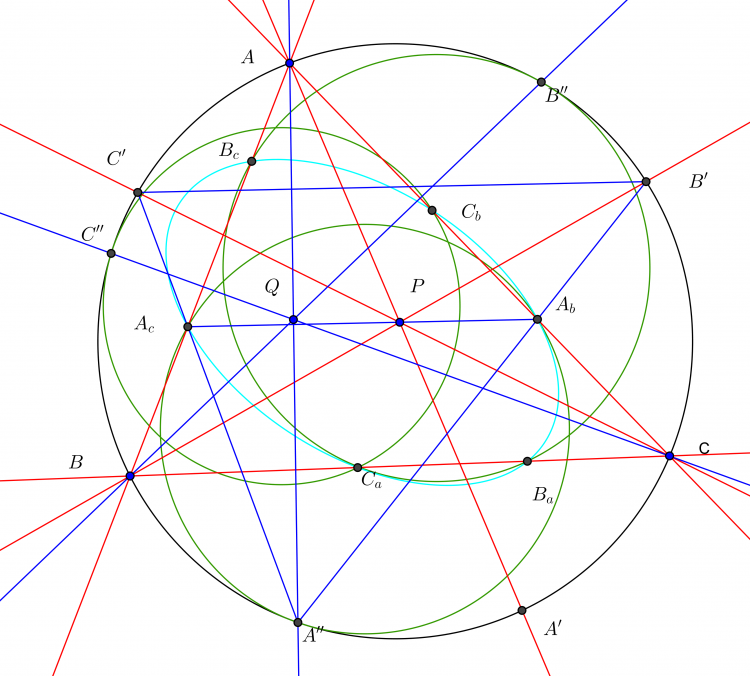
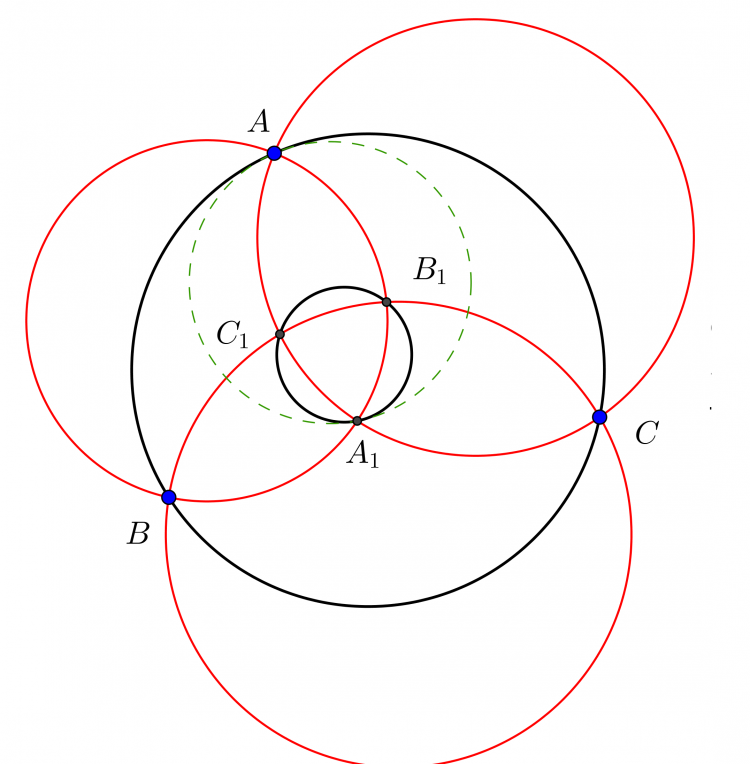
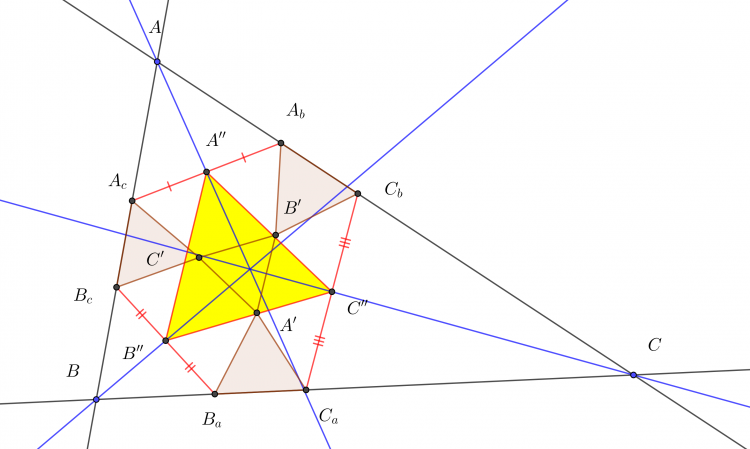
Giả thuyết: Cho sáu điểm $A, A', B, B', C, C'$ nằm trên một đường conic. Đường conic qua bốn điểm $B, B', C, C'$ cắt đường thẳng $AA'$ at $A_1, A_2$. Đường conic qua bốn điểm $C, C', A, A'$ cắt đường thẳng $CC'$  tại $B_1, B_2$. Đường conic qua bốn điểm $A, A', B, B'$ cắt đường thẳng $CC'$ tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường conic. Do đó nếu chọn trước $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng thẳng hàng.

Mở rộng định lý Pascal và định lý Brianchon

Cho sáu đường tròn $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$. Các đường tròn $(O_i)$, $(O_{i+1})$ cắt nhau tại các  điểm tại hai điểm $A_i$, $A'_i$ với $i=1, 2, 3, 4, 5, 6$ (Ở đây chúng ta lấy module 6). Chứng minh rằng nếu sáu điểm $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$ nằm trên một đường tròn và $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$  nằm trên một đường tròn khác.

1. Khi đó giao điểm của các cặp đường tròn $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ (nếu tồn tại) sẽ nằm trên một đường tròn.

2. Các đường thẳng $O_1O_4, O_2O_5, O_3O_6$ sẽ đồng quy (Vấn đề này đã được công bố tại Problem 3845, Volum 39, trên tạp chí Crux Mathemticorum)

http://tube.geogebra.org/m/1539785

TẠI SAO TÔI PHÁT HIỆN RA KẾT QUẢ NÀY?

Định lý Pascal là một định lý nổi tiếng đặt theo tên nhà bác học Blaise Pascal (1623-1662). Nội dung như sau:

Cho một lục giác nội tiếp khi đó giao điểm của các cặp cạnh đối diện nằm trên một đường thẳng.

Ngày 29/08/2015 anh Nguyễn Ngọc Giang có đăng trên facebook một kết quả là mở rộng của định lý Pascal như sau:



Tôi nhìn vào cách mở rộng của anh Giang tôi thấy rằng sẽ có một lục giác đối xứng với đường tròn ngoại tiếp lục giác $ABCDEF$ ban đầu ở bên kia trục của đường thẳng d. Với kinh nghiệm "CHƠI" hình học phẳng mấy năm nay tôi hiểu rằng kết quả này có thể mở rộng thành một định lý tổng quát hơn bằng cách ta thay lục giác đối xứng đó trong kết quả của anh Giang bằng một lục giác nội tiếp bất kỳ, ở vị trí bất kỳ trong mặt phẳng. Tôi nghĩ như vậy và tôi kiểm tra qua phần mềm thấy ý tưởng của tôi hoàn toàn đúng đắn. Quan sát kỹ hơn tôi thấy rằng cấu trúc hình học này thực ra tôi đã tìm ra và đăng trên tạp chí Crux vào tháng 5/2014(mà tôi vẫn gọi là vấn đề (hoặc định lý) tám đường tròn. Vốn được tôi biết đến như là một mở rộng của định lý Brianchon (một định lý kép của định lý Pascal).

Nội dung mở rộng định lý Pascal và định lý Brianchon như sau:

Cho sáu đường tròn $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$. Các đường tròn $(O_i)$, $(O_{i+1})$ cắt nhau tại các  điểm tại hai điểm $A_i$, $A'_i$ với $i=1, 2, 3, 4, 5, 6$ (Ở đây chúng ta lấy module 6). Chứng minh rằng nếu sáu điểm $A_1$, $A_2$, $A_3$, $A_4$, $A_5$, $A_6$ nằm trên một đường tròn và $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$  nằm trên một đường tròn khác.

1. Mở rộng định lý Pascal: Khi đó giao điểm của các cặp đường tròn $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ (nếu tồn tại) sẽ nằm trên một đường tròn (1)

Khi nào đường tròn này suy biến thành đường thẳng Pascal? Ở đây tôi chỉ ra hai cách để đường tròn này suy biến thành đường thẳng Pascal như sau:

Cách 1: Xây dựng như cách của anh Giang.

Cách 2: Nếu cho đường tròn qua $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$ suy biến thành một điểm đặt tên là điêm $M$, khi đó rõ ràng $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$ đều đi qua $M$. Giả sử các giao điểm còn lại của của $(O_1)$ và $(O_4)$,  $(O_2)$ và $(O_5)$, $(O_3)$ và $(O_6)$ là $A, B, C$ như vậy theo kết quả (1) $A, B, C, M$ nằm trên một đường tròn. Bây giờ nếu ta cho điểm M cứ tiến tới vô cùng khi đó đường tròn này sẽ biến thành một đường thẳng và $A, B, C$ chính là giao điểm của ba cặp cạnh đối diện của lục giác $A_1A_2A_3A_4A_5A_6$.

2. Mở rộng định lý Brianchon: Các đường thẳng $O_1O_4, O_2O_5, O_3O_6$ sẽ đồng quy (Vấn đề này đã được công bố tại Problem 3845, Volum 39, trên tạp chí Crux Mathemticorum)

Khi nào kết quả trên thu về định lý Brianchon? Ở đây tôi chỉ ra hai cách để kết quả trên suy biến thành định lý Brianchon.

Cách 1: Dựng hình sao cho các điểm Ai trùng với Ai' khi đó sẽ có phát biểu là:

Cho sáu đường tròn  $(O_1)$, $(O_2)$, $(O_3)$, $(O_4)$, $(O_5)$, $(O_6)$, giả sử các đường tròn $(O_i)$ tiếp xúc $(O_{i+1})$ (chúng ta lấy Modulo 6) và sáu điểm tiếp xúc này nằm trên một đường tròn khi đó đường thẳng  $O_1O_4, O_2O_5, O_3O_6$ đồng quy. Thực sự dễ dàng thấy rằng định lý Brianchon là trường hợp đặc biệt của kết quả này.

Cách 2: Cho $A'_1$, $A'_2$, $A'_3$, $A'_4$, $A'_5$, $A'_6$ suy biến thành một điểm (trùng nhau) đặt tên là điểm $M$ cho điểm này trùng với tâm đường tròn ngoại tiếp $A_1A_2A_3A_4A_5A_6$  sau đó vị tự tỉ số 2 ta sẽ có ngay định lý Brianchon.

Mở rộng định lý Lester, định lý Parry, định lý Zeeman-Gossard

Thầy Nguyễn Văn Linh chứng minh định lý mở rộng đường thẳng Simson trong file đính kèm.

   Nguyen Van Linh proof Dao generalization of the Simson line.pdf   60.35K   299 Số lần tải
 

Chứng minh khác tại đây : http://www.cut-the-k...ionSimson.shtml

Mở rộng bổ đề Sawayama

Cho tam giác $ABC$, $P$, $Q$ là hai điểm đẳng giác của nhau. $AP$, $AQ$ cắt đường tròn ngoại tiếp lần lượt tại $D, E$. Hai đường thẳng bất kỳ qua $D, E$ cắt đường tròn ngoại tiếp lần lượt tại hai điểm $T, N$ và cắt đường thẳng BC tại hai điểm $G, H$. Gọi $PG, HQ$ cắt đường tròn $(GHNT)$ tại $K, F$. Khi đó $K, F, A$ thẳng hàng.

Một giả thuyết giống định lý Cayley–Bacharach

Giả thuyết 1: Cho sáu điểm $A, A', B, B', C, C'$ cùng nằm trên một đường bậc hai và đường bậc ba (nào đó). Cho một đường bậc hai đi qua $B, B', C, C'$ và cắt đường bậc ba đó tại $A_1, A_2$. Đường bậc hai đi qua $C, C', A, A'$ và cắt đường bậc ba đó tại $B_1, B_2$. Đường bậc ba đi qua $A, A', B, B'$ và cắt đường bậc ba tại $C_1, C_2$. Khi đó sáu điểm $A_1,A_2, B_1, B_2, C_1, C_2$ nằm trên một đường bậc hai. Nếu ta chọn trước các điểm $A_1, B_1, C_1$ thẳng hàng thì các điểm $A_2, B_2, C_2$ cũng phải thẳng hàng.

Giả thuyết 2: Cho một đường conic cắt một đường bậc ba tại 6 điểm $A, B, C, D, E, F$. Cho một đường conic khác đi qua ba điểm $A,B,C$ cắt đường bậc ba tại $G, H, I$, cho đường conic khác đi qua ba điểm $D, E, F$ cắt đường bậc ba tại $J, Q, K$. Khi đó sáu điểm $G, H, I, J, Q, K$ sẽ nằm trên một đường conic.

Chứng minh giả thuyết 2:
Đây là cách chứng minh cho giả thuyết 2 của một giáo sư (mà mình không hiểu) nhưng cứ trình bày lại ra đây để mọi người tham khảo: 

Áp dụng luật nhóm, nếu như một đường bậc hai giao với một đường bậc ba tại sáu điểm thì tổng sáu điểm phải bằng không. Ta có A+B+C+D+E+F=0; A+B+C+G+H+I=0; D+E+F+J+Q+K=0 => G+H+I+J+Q+K=0 => Sáu điểm G, H, I, J, Q, K nằm trên một đường conic. Giả thuyết mạnh hơn được chứng minh.

Giả thuyết tổng quát: Cho hai đường cong (đa thức) cắt nhau tại $\frac{d^2+3d}{2}+\frac{l^2+3l}{2}+2$ điểm. Nếu $\frac{d^2+3d}{2}+1$ điểm nằm trên đường cong bậc $d$ thì $\frac{l^2+3l}{2}+1$ điểm còn lại sẽ nằm trên đường cong bậc $l$

Lời giải cho vấn đề tám đường tròn, Proposed by Đào Thanh Oai, solution by Luis Gonzalez

Liên quan đến định lý lá cờ Anh viết cùng thầy Nguyễn Minh Hà

 La co nuoc Anh.pdf   356.99K   1296 Số lần tải

Dao Thanh Oai, A family of Napoleon triangles associated with the Kiepert configuration, The Mathematical Gazette, Published online: 13 March 2015

http://journals.camb...d=0&issueId=544

 TamgiaNapoleon.pdf   309.59K   484 Số lần tải

Dao Thanh Oai, Equilateral triangles and Kiepert perspectors in complex numbers, 105--114.

 FG201509.pdf   94.99K   476 Số lần tải

Hôm qua mình có trao đổi với một cậu nước ngoại tại đây:

https://groups.yahoo...s/messages/3329

Cậu ấy viết:

Dear friends,
Consider a triangle ABC. Let I be the incenter of ABC. Draw CI such that meet the circumcircle of ABC at C’. Similarly, construct the point B’. Now, draw a line paralell to B’C’ passing throu I, such that intersect AB in I_c and AC in I_b. The lines B’I_b, C’I_c intersect at a point, E, on the circumcircle of ABC. Then, the circumcircle of triangle I_bI_cE is a mixtilinear incircle. See image attached.

I want to know whether this construction is new or not. Thanks in advance.

Best regards,
Emmanuel.



Và tìm ra một mở rộng tại đây: https://groups.yahoo...s/messages/3330


Dear Emmanuel José García, Dear Geometers,

I inspired from your construct. I posed a generalization of Mixtilinear circle as follows:

Let ABC be a triangle, P be a point on the plane, let A'B'C' be the circumcevian of P. Let a line through P and parallel to B'C', the line meets AC, AB at Ab, Ac respectively. Then B'Ab meets C'Ac at a point A'', and circle (AbAcA'') tangent with the circumcircle at A''. Define Bc, Ba, Ca, Cb cyclically , and Define B'', C'' cyclically. Then show that:

1. AA'', BB'', CC'' are concurrent.
2. Six points Ab, Ac, Bc, Ba, Ca, Cb lie on a conic



Best regards
Sincerely
Dao Thanh Oai


Tuy nhiên kết quả trên về bản chất sẽ trùng với ý tưởng của Bảo. Mình đã xác nhận tại diễn đàn đó là tuy lấy cảm hứng từ bài của Emmanuel để đưa ra mở rộng của đường tròn Mixtilinear. Nhưng kết quả này được tổng quát hóa trước đó bởi Bảo. Về mặt khoa học như thế coi như đã xác nhận kết quả này không phải của mình mà là của Bảo.

Cảm nhận riêng của mình là câu hỏi cái này quá khó để biết đúng hay sai. Nếu nó đúng thì chẳng hạn, rõ ràng sẽ giảm việc chứng minh định lý Fermat về hữu hạn trường hợp và chứng minh phương trình $1+a^n=b^n$ vô nghiệm với $n>2$, nhưng việc chứng minh định lý Fermat đã rất rất khó rồi.

 

Mình nghĩ công việc do hạn chế tầm hiểu biết có ích hơn là cố gắng bác bỏ nó cho $N_0$ nào đó đủ nhỏ.

Cảm ơn bạn đã quan tâm, vì máy tính của mình có chạy đến hết một năm cũng chưa chắc kiểm chứng được với $A, B \le 4*10^18$ nên đành nêu ý tưởng vậy thôi chứ cũng chẳng chứng minh, hay kiểm chứng được. Nhưng có một nhà toán học dự định nó sẽ đúng nếu $N_0=4$ nhưng nó yếu hơn giả thuyết $abc$.

Mình xin được viết lại ý của tác giả, vì mình không hiểu được cho đến khi đọc lại 3 lần nên có thể cmt này sẽ có ích với người khác.

 

Với mọi $N \in \mathbb{Z}_{\geq 4}$, chỉ có hữu hạn bộ 3 số nguyên dương $A,B,C$ thỏa mãn: 

1. $A+B=C,$

2. $(A,B,C)=1,$

3. $l(A,B,C) \geq N.$

Ở đây, $l(A,B,C)=\min \left\{ord_{p}(ABC)| p \in Spec(\mathbb{Z}), p | ABC \right\}$.

 

Có chỗ mình không hiểu trong phiên bản tiếng Việt là câu "tồn tại một số hữu hạn các số", hi vọng tác giả có thể nói rõ ý của mình.

 

P/S: Nếu cách diễn giải của mình đúng, số $N$ trong giả thuyết là không cần thiết vì nếu giả thuyết đúng cho $N$ thì nó đúng cho mọi $M \geq N$. Như vậy, phát biểu chỉ nên là

 

Chỉ có hữu hạn bộ 3 số nguyên dương $A,B,C$ thỏa mãn: 

1. $A+B=C,$

2. $(A,B,C)=1,$

3. $l(A,B,C) \geq 4.$

Ở đây, $l(A,B,C)=\min \left\{ord_{p}(ABC)| p \in Spec(\mathbb{Z}), p | ABC \right\}$.

Cảm ơn bạn, dùng ký hiệu mình không thạo nhưng mình có thể phát biểu bằng lời ý tưởng của mình nhé:

Nếu ba số nguyên dương $(A, B, A+B)$ nguyên tố cùng nhau thì trong phân tích ra thừa số nguyên tố của ba số $A, B, A+B$ phải có một thừa số với số mũ nhỏ hơn $N_0$, trong đó $N_0$ là một giá trị khá nhỏ  $4, 5, 6....$.

PS: Phát biểu như này thì mình không lăn tăn gì cả

1. Quan sát:
 

Cho hai hàm số liên tục $f(x)$ và $g(x)$ với $x \in [a,b]$, khi đó khả năng tồn tại một giá trị $x_0$ thực để $f(x_0)=g(x_0)$ là cao hơn so với khả năng tồn tại giá trị nguyên $y_0$ để $f(y_0)=g(y_0)$. Điều này dễ dàng hình dung qua đồ thị về giao điểm của hai hàm số liên tục và giao điểm của hai hàm số rời rạc. Đối với một đa thức khi bậc của đa thức cao lên thì độ rời rạc của đa thức $f(x)$ ($x$ nguyên) càng cao và dẫn đến giá trị $f(x)+f(y)=f(z)$ với $x,y,z$ nguyên càng trở lên khó khăn. Theo chiều hướng đó khi bậc của đa thức $k$ tăng đến một mức độ nào đó thì sẽ dẫn đến phương trình $f(x)+f(y)=f(z)$ hoàn toàn trở lên vô nghiệm. Xuất phát từ nguyên lý đó tôi đưa ra một giả thuyết như sau(chú ý giả thuyết sau chỉ là một cách để cố gắng thể hiện kết quả trong quan sát trên):

2. Giả thuyết: Cho $a$ là một số nguyên khác $0$, $m,n$ là hai số nguyên dương khác nhau, $g(x)$ là một đa thức bất kỳ cho trước, đặt $f(x)=g(x)+ax^k$, khi đó tồn tại một hằng số nguyên dương $k_0$ để với mọi $k \geq k_0$ thì phương trình:
$$f(x_1)+f(x_2)+....+f(x_n)=f(y_1)+....+f(y_m)$$
không có nghiệm nguyên dương khác một.

Chú ý: Tôi thêm chữ khác 1 vào để loại bỏ trường hợp tầm thường cho phù hợp với ý tưởng xuất phát là độ rời rạc của đa thức tăng lên khi bậc của đa thức tăng lên vì với x=1 thì f(1) không thay đổi khi ta chỉ thay đổi bậc của đa thức. Ngoài ra phản biện tại #2 của Zaraki là cho phiên bản version 1

 

Xét phép nghịch đảo tâm $A$ phương tích bất kì, ta chuyển bài toán đã cho về bài toán phụ:

Bài toán phụ. Cho tam giác $ABC,A_1$ là điểm bất kì $,B_1$ là điểm bất kì trên $BA_1,(BCB_1)$ cắt $A_1C$ ở $C_1.$ 

Chứng minh tiếp tuyến tại $A_1$ của $(AB_1C_1)$ song song với $BC.$

Bài toán phụ được chứng minh bằng cách gọi $A_1x$ là tiếp tuyến $(AB_1C_1)$ và có biến đổi góc 

$\widehat{xA_1C_1}= \widehat{A_1B_1C_1}= \widehat{A_1CB}$ suy ra đpcm.

Nhờ bạn vẽ hình lại cho mình được không? Bài toán phụ mình vẽ hình không thấy đúng. Cảm ơn bạn

Phiên bản cuối cùng của giả thuyết

Giả thuyết của anh không đúng, thử với $95800^4+217519^4+414560^4=422481^4$ (R. Frye 1988).

Thực ra, năm 1967, L. J. Lander, T. R. Parkin, and John Selfridge đã đưa ra một giả thuyết, mở rộng cho định lý Fermat lớn:

 

Nếu $k>3$ và $\sum_{i=1}^{n}a_i^k= \sum_{i=1}^mb_j^k$ trong đó $a_i \ne b_j$ với mọi thì $1 \le i \le n, 1 \le j \le m$ có nghiệm nguyên dương thì $m+n \ge k$.

 

Anh có thể xem thêm tại Euler's sum of powers conjecture.

 

Giả thuyết của anh chắc có thể đúng nếu chỉnh điều kiện từ $k \ge m+n$ thành $k>m+n$.

Cảm ơn em. Giáo sư Đào Hải Long cũng cho anh biết thông tin trên, và đưa đường link :

https://en.wikipedia...idge_conjecture

Bài toán: Cho ba đường tròn, đường tròn thứ nhất đi qua bốn điểm $B, C, B_1, C_1$, đường tròn thứ hai đi qua bốn điểm $C, A, C_1, A_1$, đường tròn thứ ba đi qua bốn điểm $A, B, A_1, B_1$. Chứng minh tồn tại một đường tròn tiếp xúc với hai đường tròn $(ABC)$, $(A_1B_1C_1)$ tại hai điểm $A, A_1$

Tam giác đều Morley, tam giác đều Napoleon luôn là chủ đề nổi tiếng và hấp dẫn đối với những ai đam mê đến hình học phẳng.  Tại chủ đề này tôi giới thiệu các bạn hơn 40 tam giác đều mới được chính tôi phát hiện. Các bạn có thể tham khảo tại link sau đây để tham khảo các kết quả này. Có rất nhiều vấn đề cần khám phá xoay quanh hơn 40 tam giác đều và họ tam giác đều này. Đây chắc chắn là những chủ đề thú vị đối vớ những ai có quan tâm đến hình học phẳng. Tôi xin trân trọng giới thiệu cùng các thầy cô và các em học sinh.

- 10 Tam giác đều thứ nhất bạn có thể xem tại đường link sau đây:

http://faculty.evans...cedInETC.html#F

- 10 tam giác đều tiếp theo bạn có thể xem tại link sau đây

https://drive.google...XnKLyw9VIl6zOhh

- Hơn hai mươi kết quả khác tôi sẽ gửi lên sau.

Đào Thanh Oai

Các bạn cho mình hỏi, sao ai đó khóa bài này của mình?

https://diendantoanh...-kinh-điển-mới/

Bài đó đã được đăng trên diễn đàn toán học cao cấp và đã có nhưng chứng minh và ủng hộ của các nhà toán học mình không hiểu tại sao lại khóa bài?

Với không gian hai chiều $f(n,m)=\frac{n}{m}=\frac{n}{2}$ 

Thấy có bài báo này trên trang web của trường đại học Princeton, mọi người cho ý kiến nhé

http://www.princeton.edu/~aloo/fermat