Mình thì thấy nhiều bài Toán tổ hợp đề bài và lời giải học sinh tiểu học cũng có thể hiểu được. Ví dụ như bài toán con ếch IMO 2016, hay bài đồng xu IMO 2014.

Em xin chém bài 4 
phần a thì  mò dễ k =3 
phần b ta cm k min =2017
Cách tô 
mỗi hàng tô 1 số cùng loại ( kể cả âm hay dương )
thì ta luôn có thoả vì lúc đó các số trên hàng k giao với cột
ta chỉ ra 1 cách mà bắt buộc k min =2017
xét bảng tô mà 2 đường chéo cạnh đường chéo lớn nhất tô trắng , 2 ô góc còn lại tô trắng và cả bảng đen
ta chỉ ra được là ô góc dưới và 2016 ô đường chéo lớn nhất k cùng mặt phẳng bờ AC với nó là các giá trị đôi 1 khác nhau 
=> k min =2017 
 

Bạn xem lại phần $b$. Đề bài nói rằng cách tô $k$-cân đối phải thỏa mãn điều kiện: Hai ô đối xứng qua đường chéo $AC$ phải điền cùng một số nguyên thuộc vào $[-k,k]$.

P/s: Xin lỗi bạn, mình hiểu nhầm ý bạn trong lời giải trên.

Hiện đã có file "Lời giải và bình luận VMO 2017" của nhóm các tác giả: thầy Trần Nam Dũng, thầy Võ Quốc Bá Cẩn, thầy Trần Quang Hùng, anh Lê Phúc Lữ, anh Nguyễn Văn Huyện. Xin up lên đây để mọi người cùng tham khảo.

File:   loi giai quoc gia - 2017.pdf   439.98K   751 Số lần tải

Hình vẽ cho bài 6:

$\boxed{\text{Bài toán 2}}$ (British MO 2014) 

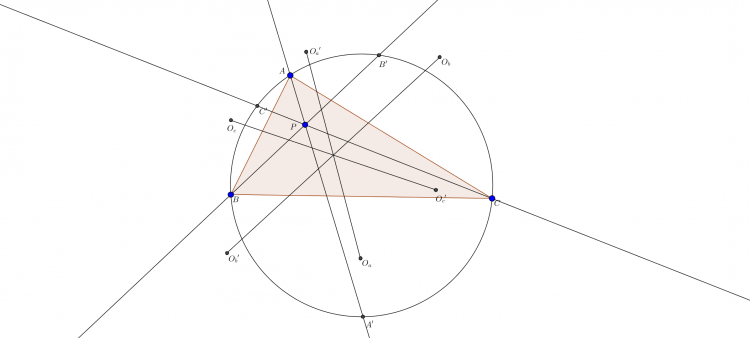
Cho tam giác $ABC$ và điểm $P$ nằm trong tam giác. Gọi giao điểm thứ hai của $AP$ với $(ABC)$ là $A'$. Các điểm $B',C'$ được xác định tương tự. Gọi $O_{a}$ là tâm đường tròn $(BCP)$. Các điểm $O_{b},O_{c}$ xác định tương tự. Gọi $O_{a}'$ là tâm đường tròn $(B'C'P)$.Các điểm $O_{b}',O_{c}'$ xác định tương tự. Chứng minh rằng $O_{a}O{a}',O_{b}O_{b}',O_{c}O_{c}'$ đồng quy.

Hình vẽ bài toán

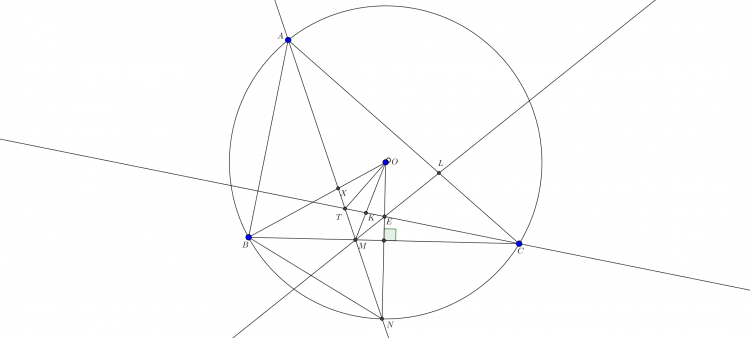
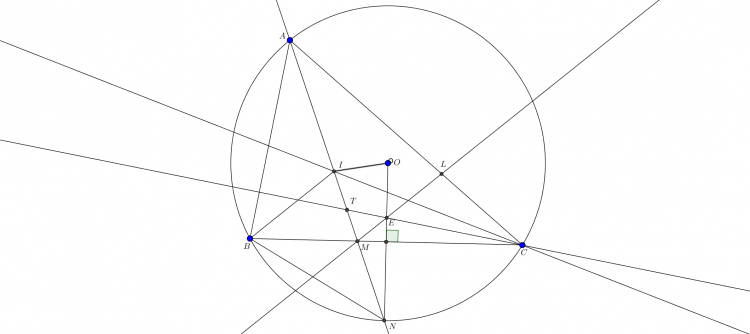
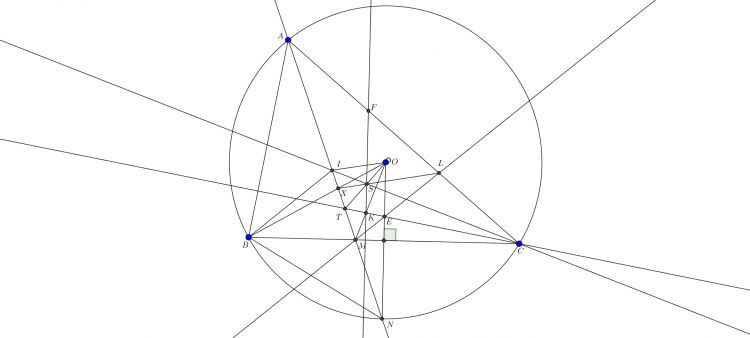
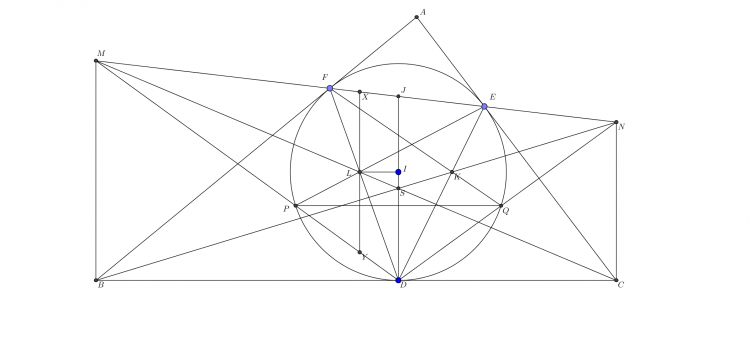
Mình xin trình bày bài giải khác, hầu như chỉ sử dụng kiến thức lớp 7 (tam giác bằng nhau, tính góc cơ bản, v.v) . Ở đây để tiện quan sát mình đã trình bày bài toán dưới dạng các bổ đề nhỏ (chia nhỏ bài toán ra). Ý tưởng của mình là chứng minh  các cặp điểm $(E;I),(K;X),(L;F)$ đối xứng qua một đường qua $O$ sau đó chỉ cần chứng minh $X,E,L\in$ một đường tròn tâm $O$ là xong. Điều này có được là nhờ sự đặc biệt của bài toán. Sau đây xin được cụ thể hóa ý tưởng này.

Trước hết, gọi $T,N$ lần lượt là giao điểm của $AI,CK$, của $OE, (ABC)$. Dễ thấy $\angle TAC=\angle TCA=30^0\Rightarrow \angle ATC=120^0, \Delta ATC$ cân tại $T$. Suy ra $TO\bot AC$ chia đôi góc $ATC$. Hơn nữa $O,N$ đối xứng qua $BC$, tam giác $OBN$ đều. Các góc sau cũng tính được dễ dàng: $\angle BCK=\angle TCI=10^0, \angle ANO=20^0,\angle OET=80^0$.

$\boxed{\text{Bổ đề 1}}$: $K,X$ đối xứng qua $TO$.

Ta có $\angle AXO=\angle BAX+\angle ABX=\frac{60^0}{2}+80^0-30^0=80^0.$. Mặt khác $\angle OKC=\angle KMC+\angle KCM=\angle NMC+\angle KCM=90^0-20^0+10^0=80^0$ (do $O,N$ đối xứng qua $BC$, tam giác $OBN$ đều). Kết hợp với $TO$ là tia phân giác góc $ATC$ suy ra $\Delta OTK=\Delta OTX\Rightarrow K,X$ đối xứng qua $TO$.

 

$\boxed{\text{Bổ đề 2}}$: $I,E$ đối xứng qua $TO$.

Thật vậy, theo một kết quả rất quen thuộc $NI=NB$, mặt khác ta đã chứng minh được $NB=NO$ nên $NI=NO$. Vậy $\Delta NOI$ cân tại $N$ và $\angle NIO=\frac{180^0-\angle ANO}{2}=80^0=\angle OET$. Vậy $\Delta OET=\Delta OIT\Rightarrow E,I$ đối xứng qua $OT(đ.p.c.m)$.

 

$\boxed{\text{Bổ đề 3}}$: $L,B$ đối xứng qua $AT$.

Thật vậy, dựng tia đối xứng với $AE$ cắt $BC$ tại $E'$. Ở bổ đề 2, ta đã chứng minh được $E,I$ đối xứng qua $TO$ mà $\Delta TAC$ cân tại $T$, vậy $\angle TAE=\angle TCI=10^0\Rightarrow \angle TAE'=10^0$. Mặt khác ta cũng có $\angle TCE'=10^0$ nên $\Delta AE'C$ cân tại $E'$, và vì vậy $E',T,O$ thẳng hàng, suy ra $\angle ATE'=\angle CTE'=120^0=\angle ATE$. Suy ra $\Delta ATE'=\Delta ATE\Rightarrow E,E'$ đối xứng qua tia phân giác góc $BAC$. vậy tia $ME$ đối xứng với $ME'$ qua $AI\Rightarrow B,L$ dối xứng qua $AI$. Phép chứng minh bổ đề 3 hoàn thành.

Tới đây ta sẽ vào bài:

Theo bổ đề 3, ta có $\angle XLA=\angle XBA=90^0-\angle ACB$, mà $\angle KFC=90^0-\angle ACB$ (do $KF\bot BC$) nên $\angle KFL=\angle XLF$ kết hợp với bổ đề 2 ta suy ra $F,L$ đối xứng qua $TO$. Công việc còn lại là đi chứng minh $E,X,L\in$ 1 dường tròn tâm $O$. Ta có $\angle XOE=60^0, \angle XTE=120^0\Rightarrow XTEO$ nội tiếp. Hơn nữa, theo một kết quả cơ bản khác, $TO$ là tia phân giác $\angle XTE$ suy ra $\Delta XOE$ cân tại $O$ và nó thực sự là một tam giác đều. Tiếp tục, $\angle XLE=\angle XBC=30^0$ (theo bổ đề 3) nên ta có $X,E,L$ nội tiếp một dường tròn tâm $O$ là $Γ$. Dễ thấy theo tính chất đối xứng từ các bổ đề 1, 2 ta có $K,X,I,E,L,F\in Γ, đ.p.c.m$!

P/s: Ta có thêm một số kết quả sau:

1) $KF, XL, TO, CI, AE$ đồng quy tại $S$.

2) Gọi $J$ là giao điểm của đường cao hạ từ $C$ xuống $AB$ với $(ABC)$ thì $J,O,I$ thẳng hàng.

và còn nhiều kết quả khác, mời các bạn khám phá.

$$\begin{array}{| I | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline \end{array}$$

Lời giải bài toán 83.

...Theo định Lý $\text{Brocard}$ ta có: $O$ là trực tâm của tam giác $AMI$ $\Rightarrow IM \perp OA$ $(2)$

Từ $(1)$ và $(2)$ $\Rightarrow I,M,P$ thẳng hàng

Vậy Chứng minh rằng $MP; BB_{1}; CC_{1}$ đồng quy tại $1$ điểm.

Chỗ này dùng Brocard hơi quá tay, hơn nữa Brocard không được học ở chương trình toán THCS! (chứng minh định lý này cũng không đơn giản) Để giải quyết chỗ này ta nên dùng ý tưởng trục đẳng phương thì hay hơn (mình biết là khái niệm này không được học, nhưng về ý tưởng thì đơn giản và sáng sủa hơn rất nhiều!).

Mình có ý tưởng cho câu b bài 5, đã đăng lên bên AOPS. Xin đăng lại ở đây; bạn đọc kiểm tra dùm.

Trước hết ta nhận thấy rằng nếu $d=2n-1$ thì tồn tại một bộ số như vậy:

$$n,n-1,n-2,\dots ,3,2,1,2,3,\dots ,n-2,n-1,n$$

Để hoàn tất chứng minh, ta chỉ ra rằng với mỗi $d$ nguyên dương, số $n$ nhỏ nhất sao cho $|S_n(d)|>0$ thì không nhỏ hơn $\frac{d+1}{2}$, bằng quy nạp.

Trường hợp $d=1$ hiển nhiên đúng.

Giả sử $k+1$ là số nguyên dương nhỏ nhất mà mệnh đề trên sai. Khi đó tồn tại một bộ $k+1$-số sao cho $n< \frac{k+2}{2}$. Khi đó phải tồn tại hai chỉ số $i,j$ sao cho $x_i=x_j$ và $|i-j|$ nhỏ nhất có thể. Khi đó mọi số nguyên nằm giữa $x_i,x_j$ chỉ xuất hiện đúng một lần, suy ra phải có một số $m$ nào đó xuất hiện ba lần. Ta thấy rằng bộ $k+1$-số bị cắt thành bốn đoạn (có thể rỗng) bởi $m$:

$$\{S_1\}m\{S_2\}m\{S_3\}m\{S_4\}$$

Câu 4a khá đơn giản. Ta chia mảnh đất thành $10$ hình chữ nhật kích thước $30\times 40$. Khi đó sẽ tồn tại một hình chữ nhật không tâm bồn hoa nào ở phần trong (không kể cạnh của nó). Khi đó phần trung tâm $25\times 35$ của hình chữ nhật này không cắt bồn hoa nào.

Lời giải bài 9:

Giả sử tồn tại các số $\alpha <\beta <\gamma $ khác 1 thoả mãn tập ${{\mathbb{Z}}^{+}}$ có thể phân hoạch thành 3 tập $S\left( \alpha  \right)$, $S\left( \beta  \right)$ và $S\left( \gamma  \right)$.

Vì $\alpha <\beta <\gamma $ nên suy ra $1\in S\left( \alpha  \right)$ hay $\left\lfloor \alpha  \right\rfloor =1$. Khi đó: $\alpha =1+\delta $ với $0<\delta <1$.

Nếu số tự nhiên $n\in S\left( \alpha  \right)$ thì tồn tại số nguyên dương $k$ sao cho:

$n=\left\lfloor k\alpha  \right\rfloor \Rightarrow k\alpha <n+1\Rightarrow \left( k+1 \right)\alpha <n+1+\alpha =n+2+\delta <n+3$

Suy ra $\left\lfloor \left( k+1 \right)\alpha  \right\rfloor \le n+2$, hay không tồn tại 2 số nguyên dương liên tiếp không thuộc $S\left( \alpha  \right)$.                                            (1)

Chỗ (1) mình thấy không ổn, chưa thể kết luận là không có hai số nguyên liên tiếp nào thuộc $S(\alpha)$. Nếu ta chọn $\alpha$ rất nhỏ, gần $1$ thì khi đó $S(\alpha)$ vẫn chứa rất nhiều số nguyên dương từ $1$ tới $m$ nào đó.

Đề bài 9 đúng phải là: với mỗi số thực dương $\alpha$, ta gọi $S(\alpha)=${$[n\alpha]|n\in \mathbb {Z^+}$}. Chứng minh rằng $\mathbb {Z^+}$ không thể biểu diễn thành hợp của 3 tập rời nhau $S(\alpha)$, $S(\beta)$, $S(\gamma)$.

Bài 5:

Có $17$ nhà bác học viết thư cho nhau trao đổi $3$ vấn đề. Chứng minh rằng luôn tìm được $3$ người cùng trao đổi một vấn đề.

 

Bài toán này khá nổi tiếng, từng là bài thi Olympic quốc tế năm 1964. Nó còn liên quan đến Định lý Ramsey trong lý thuyết đồ thị.

 2016-vie.pdf   168.36K   765 Số lần tải

Đề phiên bản Tiếng Việt đây, các mem chém đi nhé

 

Đáp số: $7$.

Trước hết nhận xét về hàm $f$. Phương trình $f(x)=0$ có ba nghiệm thực phân biệt $x_1\in (-1,0),\ x_2\in (0,1),\ x_3\in (2,3)$, và $f$ có giá trị cực đại là $1$, giá trị cực tiểu là $-3$. Bây giờ xét phương trình $f(f(x))=0$. Rõ ràng nếu $x_0$ là nghiệm của phương trình này thì $f(x_0)$ là nghiệm của phương trình $f(x)=0$, do đó phương trình $f(f(x))=0$ tương đương với

Xét hàm số $g(x)=f(x)-x_1$. Hàm số này có giá trị cực đại là $1-x_1>0$ và giá trị cực tiểu là $-3-x_1<0$. Do đó phương trình $f(x)=x_1$ có ba nghiệm thực phân biệt. Tương tự ta phương trình $f(x)=x_2$ cũng có ba nghiệm thực phân biệt. Còn hàm số $h(x)=f(x)-x_3$ có giá trị cực đại là $1-x_3<0$ nên phương trình $f(x)=x_3$ có một nghiệm duy nhất. Vậy tóm lại, phương trình đã cho $f(f(x))=0$ có đúng $7$ nghiệm.

 

Chọn bộ (a,b,c)=(2,2,1/4) thì ca+a+1 # ab+a+1

$ca+c+1$ chứ không phải $ca+a+1$!

Cách bạn có vài chỗ khác cách mình, nên mình không hiểu cái chỗ đó.

 

 

2 cái dòng cuối là mình không hiểu đó bạn.

Có lẽ bạn chưa hiểu kí hiệu $\nu_{5}(\dots)$. Kí hiệu này chỉ số mũ đúng của $5$ (có thể thay $5$ bởi số nguyên tố $p$ bất kỳ) trong phân tích thành thừa số nguyên tố của một số nguyên, tức là nếu ta có $5^k|n$ nhưng $5^{k+1}\not |n$ thì $\nu_{5}(n)=k$. Như vậy hai lời giải đều hoàn toàn như nhau.

Về bài toán $7$, mình nghĩ nó là biến thể của bài toán sau:

(Tournament of towns) Có một số tấm thẻ mà trên đó điền các số nguyên không vượt quá $n$ sao cho tổng các số ghi trên các tấm thẻ này là $k\cdot n!$. Chứng minh rằng ta có thể chia các tấm thẻ này thành $k$ đống, mỗi đống có tổng các số ghi trên các tấm thẻ đúng bằng $n!$.

Lời giải cho bài $3$ mà mình lấy được từ AOPS:

Bài 4 đề chuyên:

Từ đề bài ra ta dễ dàng có $(2n)^2-1=3(2a+1)^2$. Ta cần chứng minh tồn tại số tự nhiên $m$ sao cho $m^2+(m+1)^2=n$, hay $2n-1=(2m+1)^2$. Giả sử $3|2n-1$, khi đó $2n+1\equiv 2 \pmod 3$ và $2n-1=3(2b+1)^2,\ 2n+1=(2c+1)^2$, vô lí. Vậy $3|2n+1$ và $2n-1=(2m+1)^2$, đpcm. $\square$

Định lý Erdos-Ginzburg-Ziv: Trong $2n-1$ số nguyên bất kỳ, tồn tại $n$ số có tổng chia hết cho $n$.

Mình nghĩ  $a_{2k}=2a_k+1=3$ chứ nhỉ ? 

Chết, sai rồi =), để mình sửa, cám ơn bạn. Nói chung không ảnh hưởng gì nhiều.

Câu 3:

Mình giải quyết như sau:

Đặt $X=(K)\cap BC,Y=(L)\cap BC$.

$\angle INB=\angle IMC=90^0-\frac{\angle BAC}{2}$ (do $AMN$ cân tại $A$),

$\angle NIB=\angle AMN-\angle NBI=90^0-\frac{\angle BAC}{2}-\frac{\angle ABC}{2}=\frac{\angle ACB}{2}=\angle ICX$. Vậy $\Delta NIB$ và $\Delta MCI$ đồng dạng, suy ra $\frac{IB}{IC}=\frac{IN}{CM}=\frac{BN}{IM}$, suy ra $\frac {IB^2}{IC^2}=\frac{BN}{CM}$ (Do $IM=IN$). Ngoài ra ta cũng dễ cm được hai tam giác $IFN$ và $EIM$ cũng đồng dạng, suy ra $\angle FIN=\angle EIM$ và $\frac{IE^2}{IF^2}=\frac{EM}{FN}\Rightarrow \frac{IB}{IC}=\frac{IF}{IE}(*)$.

Đến đây, ta lại có $\angle FYB=\angle FIB=\angle FIN+\angle NIB=\angle IEM+\angle ICM=\angle IXY+\angle IXE=\angle EXY$

$\Rightarrow EX||FY\Rightarrow I,L,K$ thẳng hàng.

b) Câu này ta sẽ cm $BYFQ, CXEP$ là các hình thang cân, suy ra $BY=FQ,XC=PE$. Kết hợp với $BY=XC$ sẽ có ngay $đpcm$.

Thật vậy, dễ thấy $KL$ là trục $đx$ của hình thang $FYXE$ suy ra nó là hình thang cân, tới đây dễ suy ra $BYFQ, CXEP$ là các hình thang cân. 

Ta gọi $T$ là giao điểm của tiếp tuyến chung trong của $(K), (L)$ với $BC$. Thế thì $TY.TB=TX.TC$. Ta có (dễ cm được) các cặp tam giác sau đồng dạng: $TIY,IBF$ và $TIX,ICE$. từ đó ta có các kết quả sau:

$\frac{TI}{IB}=\frac{TY}{IF}, \frac{TI}{IC}=\frac{TX}{IE}$,
$\Rightarrow \frac{IB}{IC}=\frac{TY.IF}{TX.IE}$, kết hợp với $(*)$ suy ra $TY=TX\Rightarrow BY=CX\Rightarrow FQ=EP (đpcm)$.

Câu 4: Mình làm như thế này:

Ta thấy rằng $2016=2^5.3^2.7$, mà $3^2.7=1+2(1+2(1+2(1+2(1+2.1))))$, vậy nên nếu $a_k=1$ là một số hạng của dãy thì 

$a_{2k}=2a_k+1=3$

$a_{4k}=2a_{2k}+1=7$

...

$a_{2^5.k}=63$
$a_{2(2^5.k+1)-1}=63.2$

...

$a_{2^5.(2^5.k+1)-1}=63.2^5=2016$.

Nếu ta cm được có vô hạn số hạng $a_{k}=1$ của dãy, thì như vậy, tồn tại vô hạn số hạng $a_{2^5(2^5.k+1)-1}$ tương ứng có giá trị $2016$.

Thật vậy, ta để ý rằng có vô hạn số hạng $0$ trong dãy vì từ số hạng một $a_i=0$ ta có được $a_{2i+1}=2a_i=0$, dẫn tới tồn tại một dãy vô hạn các số $0$. Điều này xảy ra nếu ta chọn $i=1$. Chú ý rằng dãy trên gồm toàn các số hạng có chỉ số lẻ, nên từ đẳng thức $a_{2n}=a_{2n+1}+1$, ta suy ra tồn tại một dãy con vô hạn của dãy đầu gồm toàn các số $1$, suy $đpcm$.

 

P/s: Vì là từ phép suy luận ngược, dựa vào công thức truy hồi của dãy nên có lẽ công thức trên cho ta tất cả các số hạng $2016$ của dãy. (?) Khi đó câu thứ hai có thể giải quyết khá dễ dàng, chỉ số nhỏ nhất đó là $2^5(2.2^5+1)-1=2079$.

Một cách tiếp cận khác, nhẹ nhàng hơn cho câu 6 c):

Đặt $J=DI\cap EF,S=BN\cap CM$. Kẻ đường thẳng vuông góc với $IL$, cắt $EF$ tại $X$, $DP$ tại $Y$. Dễ thấy $D,S,I,J$ thẳng hàng. Theo định lý Pascal, $B,N,K,S$ thẳng hàng, tương tự với $C,M,L,S$. Hơn nữa, theo bổ đề hình thang, $S$ là trung điểm $JD$, theo định lý con bướm $LX=LY$. Vậy $XY//JD\Rightarrow XY\bot BC$, tức là $IL//BC\Rightarrow K,I,L$ thẳng hàng $(đpcm)$.

Hiện đã có file danh sách kết quả của kỳ thi VMO năm 2017 (mình lấy trên mạng, nhưng 99.99% là chính xác):
http://www.mediafire...SGQG_2017-1.pdf
Ngoài ra theo thông tin từ thầy Trần Nam Dũng, giáo viên trường ĐHQG TPHCM thì năm nay có 1 bạn lớp 10 đạt giải Nhất, kết quả một số tỉnh như sau:
Hà Tĩnh: 5 nhì, 4 ba
Vũng Tàu, 1 nhất, 1 nhì, 2 ba, 1 kk
Vĩnh Phúc có ít nhất là 3 giải nhì
Hạ Long 1 nhì, 2 ba, 5 kk
Binh Thuận 1 ba, 3 kk
Đồng Nai 1 ba
Ninh Bình 2 kk
Hà Nội toàn đoàn có giải, trong đó 3 Nhất.
Xin chúc mừng tất cả các bạn đạt giải trong kỳ thi năm nay.
Các mem của VMF ai có giải xin giơ tay!
P/s: Cá nhân mình cũng tham gia nhưng không đạt giải.

 

Xem xong file thì mình thấy có rất nhiều đoàn đạt giải toàn đoàn, trong đó đặc biệt là Nghệ An (không tính đến ĐH Vinh) với 10 giải Nhì!
P/s: Các bạn baopbc, canhhoang30011999, Nguyen Dinh Hoang team Nghệ An này!

 

Thêm một số thông tin từ thầy Nam Dũng: năm nay cut-off cho các giải từ nhất tới KK là 28:22.5:18:14. Điểm để dự thi TST (chọn đội tuyển IMO) là 23.