Câu 3b)

Hình

Tớ không thi nhưng đây là lời giải bài hình của tớ (Mong ad post dù e k biết latex nhưng các bạn đang cần lời giải)

Câu 2: Dạng toán này đòi hỏi cần tìm được tiếp điểm, nếu không gần như là vô vọng   

Hướng 2: Phát hiện 1 số tính chất, như sau (cho những bạn chưa được học về phép nghịch đảo giống mình  )

Bài 4: Gọi $E$ là điểm bất kì trên $d$, $AB$ cắt $OH$ tại $C$

$P(C/E)=CH^2=CA.CB=P(C/O)=OC^2-R^2$

Câu dãy ngày 1 là một ứng dụng đẹp của đa thức Chebyshev trong số học 

Xét bài toán tổng quát sau: Cho p nguyên tố lẻ, (xn): x₁=1, x2=p, x_n+2=2px_n+1-x_n. CMR A=x_2m + 1 / p+1 là số chính phương với mọi m.

Giải:

Xét các đa thức Chebyshev loại 1 và loại 2:

T₀(x)=1, T₁(x)=x, Tn+2(x)=2xT_n+1(x)-Tn(x)

U_o(x)=1, U₁(x)=2x,U_n+2(x)=2xU_n+1(x)-U_n(x)

Ta CM định lí sau:

$U_n(cosx)=\frac{sin(n+1)x}{sinx}$

CM: Ta sẽ cm bằng phương pháp quy nạp theo n

+ Dễ thấy nó đúng với n=0,1

+ Gs đúng tới n=k, khi đó:

Áp dụng ngay vào bài ta có ĐPCM 

Hai cách tiếp cận khác nhẹ nhàng hơn cho bài toán 2 

Cách 1:

Đặt p=2013, ta thấy phương trình đặc trưng xác định dãy là t²=2pt-1 <=> Delta'=p²-1>0

Vậy có 2 nghiệm $t_1=p+\sqrt{p^2-1}$ và $t_2=p+\sqrt{p^2-1}$

Thay n=1,2 ta giải hệ phương trình thì được: $x_n=\frac{t_1^{n-1}+t_2^{n-1}}{2}$

Từ đó $\frac{x_{p+1}+1}{p+1}=\frac{(t_1^{p/2}+t_2^{p-2})^2}{2(p+1)}$ 

Chú ý t₁+t₂=2p và t₁t₂=1 nên đặt căn nhân tử và phân tử theo định thức Newton ta được kết quả là N² (N nguyên)

Cách 1: 

Tương tự như trên, nhưng chú ý x_n+2=(4p²-2)x_n-x_n-2

Xét dãy (y_n) thỏa mãn y₁=1, y₂=2p-1, y_n+2=2py_n+1-y_n

Ta sẽ CM quy nạp biểu thức  $\frac{x_{2n+1}+1}{p+1}$ chính là y_n² (*)

Với n=1,2 khẳng định đúng

Theo hệ thức quen thuộc của dãy tuyến tính bậc 2 thì y_n.y_n+2-y_n+1²=y₁.y₃-y₂²=2p-2

Từ đó áp dụng giả thiết quy nạp và sử dụng chú ý thì ta được  $\frac{x_{2n+4}+1}{p+1}$=y_n+2²

Từ đó theo nguyên lí quy nạp (*) được CM

Vì vậy áp dụng vào bài ta cũng được ĐPCM

Bài 1 của em ạ:

Bổ đề: Cho $2$ đường tròn $(O_1), (O_2)$ và điểm $M$, $H$ là hình chiếu của $M$ lên tđp của $2$ đg tròn thì $P(M/O1)-P(M/O2)=2O1O2.HM$

Bài $3$: Lấy $S$ là chân đg cao từ $A$, $ID$ cắt $XY$ tại $J$, $AJ$ cắt $(O)$ tại $E$ thì $JA_1.JA_2=JA.JE=JH.JD$ với $ID$ giao $(DA_1A_2)$ tại $H$

Khi đó $P(J/O)=JA.JE=R^2-JO^2=R^2-(PD^2+(AS-AH)^2/4)=R^2-(b-c)^2/4-(RcosBcosC)^2=k$

Bài $4$: IMO Shortlist $2012$

Bài $6$: Chứng minh bằng quy nạp theo $n$ (Kí hiệu hàm phi bởi $o$)

Giả sử đúng đến $m=k$ tồn tại vô số $n$ để $k|3.2^n+n$

Ta sẽ chứng minh nó đúng với $k+1$ tức tồn tại vô số $s$ để $k+1|3.2^s+s$

Chú ý rằng $o(k+1)<k+1$ nên tồn tại $r$ để $o(k+1)|3.2^r+r$

Ta chọn $s$ sao cho $o(k+1)$, $k+1|s+3.2^u$ (luôn tồn tại theo định lí Thặng dư Trung Hoa)

Nếu $k+1$ chẵn, đặt $k+1=2^a.b$ lúc đó đặt $s=2^c.d$ với $c>a$ do đó $k+1|3.2^u(2^{s-u}-1)$ (do $o(k+1)|s-u$ và $v_2(k+1)<u$) nên $k+1|3.(2^s-2^u)$

Nếu $k+1$ lẻ thì cmtt như trên kết hợp lại ta có $k+1|3(2^s-2^u)$ nên $k+1|3.2^s+s$ từ đó tồn tại $s$, gt quy nạp hoàn tất và ta có ĐPCM

 Bổ đề Cho tam giác $ABC$, tiếp tuyến tại $A, C$ cắt nhau tại $E$. Khi đó: $sinAEB/sinCEB=(AC/BC)^2$

$sinAEB/sinCEB=sinAEB/sinBAE.sinBAE/sinBCE.sinBCE/sinBEC=AB/BE.sinBCA/sinBAC.BE/AC=(AB/AC)^2$

Áp dụng định lí $Ceva$ sin cho 3 đường $BAb, CAc, AA1$ đồng quy tại $A1$

$3$ câu hình

Lần $1:$ 

$a)$ Dễ CM $OM=ON$ và $PM=PN$ bằng cộng góc đơn giản từ đó dễ suy ra $H,I$ đối xứng qua $d$

$b)$ Áp dụng câu $a$ ta chuyển ĐPCM thành $AH$ đi qua tđ $D$ của $BC$. Áp dụng định lí $Menelaus$ với chú ý $OMN$ ~ $E'BC$ với $E'$ là điểm chính giữa cung lớn $BC$, gọi $K$ là trực tâm $E'BC$ và dễ CM $E'K=2OD$ và $DK.DE'=DB.DC=DE.DK$ hay $DE=DK$ từ đó ta được ĐPCM

Lần 2:

a) Dễ thấy $T$ là $(AEF)$ giao $(O)$ từ đó áp dụng t/c trục đẳng phương cho $(AEF), (BEFC) và (O)$ đc $A,T,G$ thẳng hàng

Bài hình 

Câu $3$:

Bài $4$:

Ta giải quyết bài toán tổng quát với bảng $2n.2n$

Dựa vào quan hệ bài toán ta có thể liên tưởng tới sự quen nhau của $2n$ người được đánh dấu thành bảng $2n.2n$

Ta coi $x[i,j]=0$ thì $i,j$ không quen nhau còn $x[i,j]=1$ thì $i,j$ quen nhau

Xét tổng $S_{j,j'}=\sum_{i=1, i\neq j,j'}^{2n}x_{ij}x_{ij'}$ (dễ thấy $2$ ô cột $j,j'$ không ảnh hưởng đến mod $2$)

Nói cách khác, ta đưa bài toán về cm trong $2n$ người bất kì luôn có số người quen chung là số chẵn

$CM$: Giả sử phản chứng rằng hai người bất kì trong nhóm đều có số người quen chung là lẻ

$TH1$: Tồn tại $1$ người có số người quen là lẻ

Gọi đó là $A$, tập người quen của $A$ là $(A_1,...A_k)$ với $k$ lẻ

Xét mối quan hệ trong nhóm $k$ người này nếu người nào cũng quen lẻ người thì tổng số mối quen biết là lẻ mà theo bổ đề bắt tay thì tổng chẵn vậy vô lí

Điều đó chứng tỏ tồn tại $A_i$ để $(A,A_i)$ có số người quen chung là chẵn từ đó dễ thấy tồn tại $S(A,A_i)$ chẵn

$TH2$: Tất cả đều quen chẵn người

Gọi người có nhiều người quen nhất là $A$, trong đó $X_1$ là tập người quen của A, $X_2$ là phần còn lại

Dễ thấy $|X_1|+|X_2|=2n-1$ là số lẻ nên $|X_2|$ lẻ

Theo giả sử phản chứng, mỗi bạn trong $X_1$ có số người quen chung với $X_1$ là lẻ, mà nó có chẵn người quen nên quen lẻ người trong $X_2$

Tương tự với, mỗi người trong $X_2$ cũng quen lẻ người trong $X_1$ và lẻ người trong $X_2$

Ta đếm bằng $2$ cách số cặp $V=(B,C)$ trong đó $B,C$ quen nhau mà $B$ nằm trong $X_1$, $C$ nằm trong $X_2$

+ Với $B \in X_1$, do $B$ quen lẻ người trong $X_2$ mà $|X_2|$ lẻ nên $V$ lẻ

+ Với $C \in X_2$, do $C$ quen lẻ người trong $X_1$ mà $|X_1|$ chẵn nên $V$ chẵn

Từ $2$ điều trên ta thấy vô lí tức gs phản chứng sai. Vậy tồn tại $S$ chẵn, thay $n=1009$ ta có kết quả của bài toán $\blacksquare$  

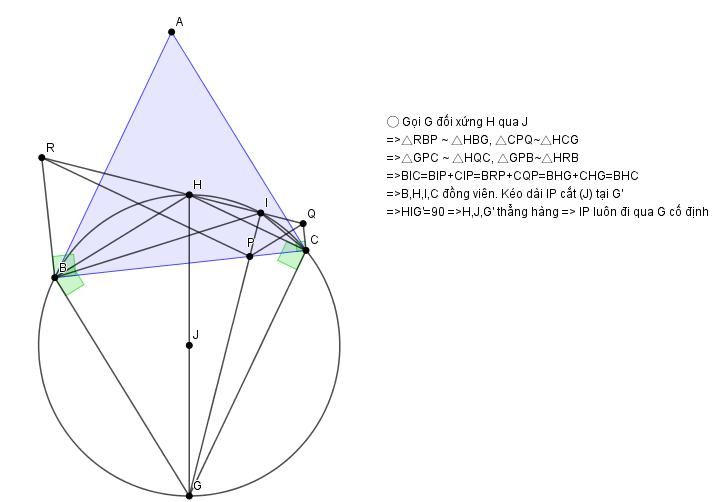
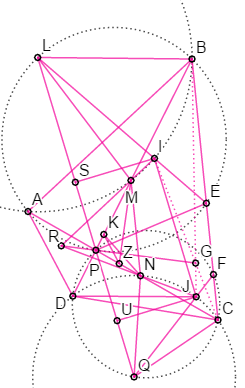
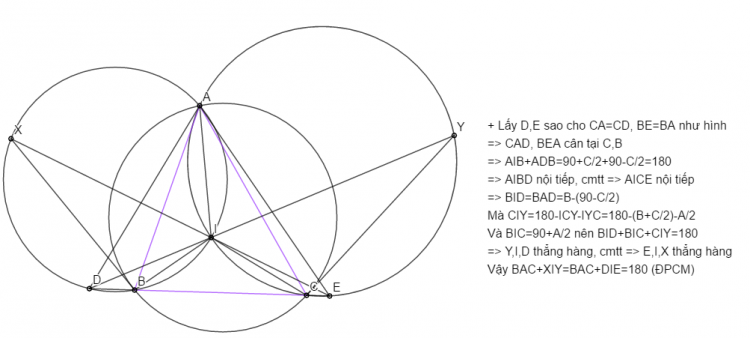
Bài $7$: Câu $a$ từng nằm trong đề thi HSG Lớp 10 trường ĐHSP năm nay, vẽ hình rất khó  

a) Gọi $L,Q$ là tâm $(AIB)$, $(AJC)$; $S,U$ là hình chiếu của $I,J$ trên $LQ$

Có $PEF=PAB=PDC=PFE$ nên $PE=PF$ đồng thời $LPB+QPC=1/2(AEB+DFC)=DPC \Rightarrow  L,P,Q $ thẳng hàng

Do $PLB=PEF=PFE=PQC$ và $PBL=PBA+ABL=PCD+DCQ=PCQ$ nên $PBL$ ~ $PCQ$ do đó $PB/BL=PC/CQ$ 

Ta có: $IS/JU=IL.sinPBC/JQ.sinPCB=LB/QC.PC/PB=LB/PB.PC/QC=1$ 

Vậy $d(I/LQ)=d(J/LQ)$ nên $IJ//LQ$ do đó $JIB+JCB=JIE+EIB+C/2= PAE+90+EAB/2+90-A/2=180+(PAE-DAE/2)=180$

(do $PAD=PBE=PAE$ nên $AP$ là pg $DAE$). Từ đó $(BICJ)$ đồng viên và ta có ĐPCM

{ Đề lớp 11 }

Bài 1:

Bài 4:

Bài 3: