ĐỀ THI OLYMPIC CHUYÊN KHTN 2018
Ngày thi thứ nhất
Câu 1: Tìm tất cả các số nguyên $a \ne 1$ sao cho:
$A=\dfrac{a^6-1}{a-1}$
là số chính phương.
Câu 2: Tìm tất cả đa thức hệ số thực $P(x)$ thỏa mãn $ P(0)=1 $ và
$ P(x^2+1)=(P(x)^2)+2xP(x)$
với mọi $x \in \mathbb{R}$
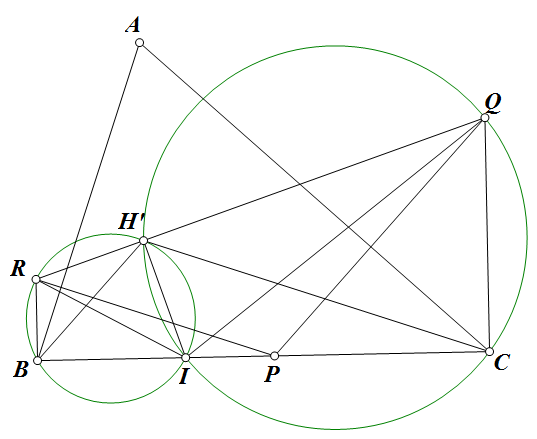
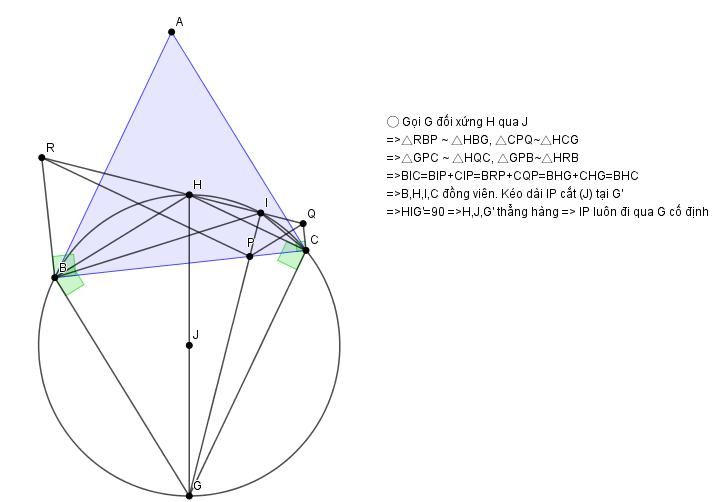
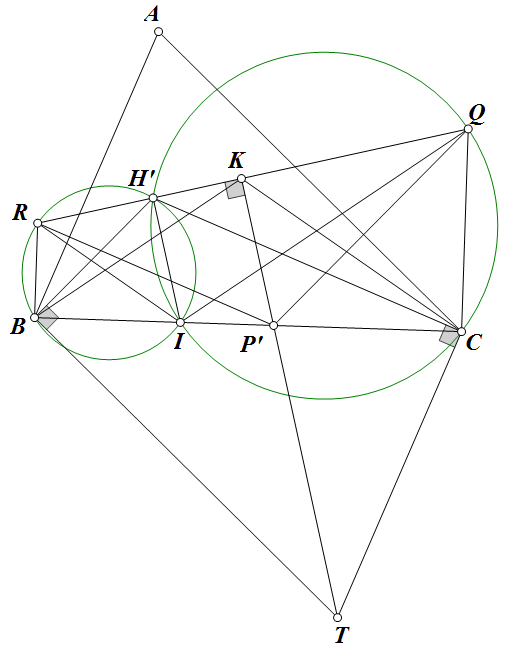
Câu 3: Cho tam giác $ ABC $ nhọn có trực tâm $ H $. Điểm $ P $ di chuyển trên cạnh $ BC $. Lấy các điểm $ Q $ và $ R $ sao cho $ PQ \perp CA, CQ \perp BC, PR \perp AB, BR \perp BC $.
a) Chứng minh rằng đường thẳng $QR $ đi qua $ H $.
b) Chứng minh rằng đường thẳng qua $ P $ vuông góc với $ QR $ luôn đi qua một điểm cố định khi $ P $ thay đổi.
Câu 4: Cho $ a,b,c $ là các số thực dương. Chứng minh rằng:
$ \sqrt{\dfrac{a^2+bc}{a(b+c)}}+\sqrt{\dfrac{b^2+ca}{b(c+a)}}+\sqrt{\dfrac{c^2+ab}{c(a+b)}}+\sqrt{\dfrac{8abc}{(a+b)(b+c)(c+a)}} \ge 4 $
Ngày thi thứ hai
Câu 5: Cho dãy số nguyên dương $ (a_n) $ thỏa mãn $a_{n+1}=a_n^3+4a_n$ với mọi $ n \ge 1 $.
Tìm giá trị nhỏ nhất của $a_1$ để $ a_{2018}+2018 $ chia hết cho $ 57 $.
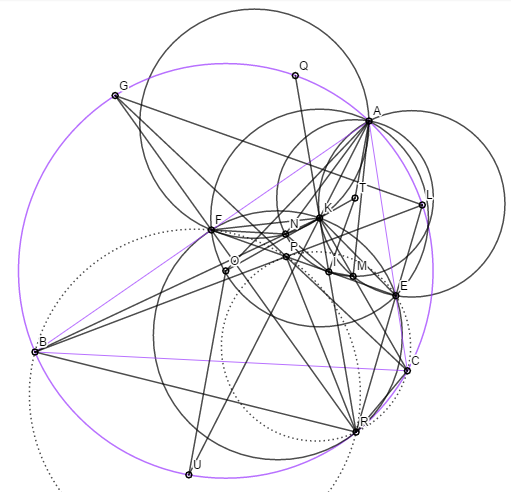
Câu 6: Cho tam giác $ ABC $ nhọn có trực tâm $ H $. Các điểm $ E, F $ lần lượt thuộc các đoạn thẳng $ CA, AB $ sao cho $ EF $ tiếp xúc với đường tròn ngoại tiếp tam giác $ BHC $. $ K $ là tâm ngoại tiếp tam giác $ AEF $. $ KC,KB $ lần lượt cắt các đường tròn ngoại tiếp tam giác $ KAE,KAF $ theo thứ tự tại $ M,N $ khác $ K $. Chứng minh rằng $ EF $ tiếp xúc với đường tròn ngoại tiếp tam giác $ AMN $.
Câu 7: Cho $ n \ge 3 $ là số nguyên dương. Trong mặt phẳng tọa độ $ Oxy $, giả sử tồn tại một đa giác lồi $ n $ cạnh thỏa mãn các điều kiện sau:
-Mỗi đỉnh của đa giác có hoành độ, tung độ là các số hữu tỉ.
-Tất cả $ n $ cạnh của đa giác có độ dài bằng nhau.
Chứng minh rằng $ n $ là số chẵn.
Bài viết đã được chỉnh sửa nội dung bởi anhquannbk: 06-05-2018 - 11:59