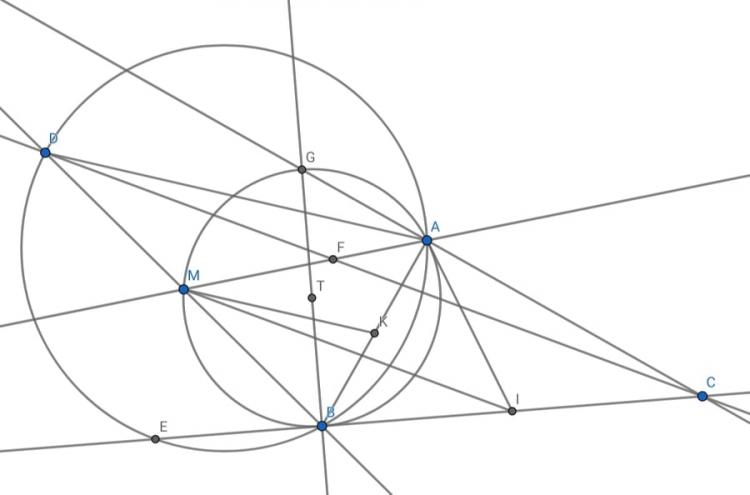
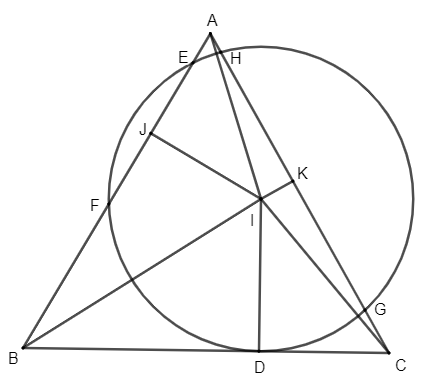
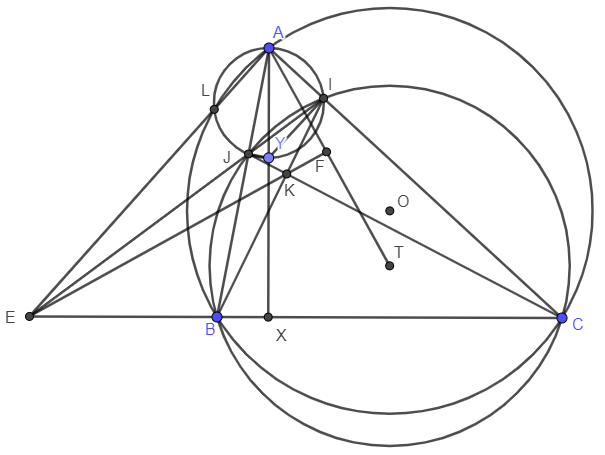
$\boxed{28}$ Cho tam giác $ABC$ vuông cân tại $A$. $M$ là trung điểm của $AC$, trên $BM$ lấy $N$ sao cho $AM=MN$. $CN$ cắt $AB$ tại $E$ Chứng minh rằng: $BN=AE$

Screenshot (22).png

Đặt AB = AC = a. Tính được $BM=\frac{\sqrt{5}}{2}a$, $BN=\frac{\sqrt{5}-1}{2}a$.

Áp dụng định lý Menelaus cho tam giác BAM ta có:

$\frac{EB}{EA}.\frac{CA}{CM}.\frac{NM}{NB}=1\Rightarrow \frac{EA}{EB}=\frac{2}{\sqrt{5}-1}\Rightarrow \frac{EA}{AB}=\frac{2}{\sqrt{5}+1}=\frac{\sqrt{5}-1}{2}=\frac{BN}{AB}\Rightarrow EA=BN$

Bài 7: Cho tam giác $ABC$ nhọn có $AB<AC$. Gọi $K$ là điểm bất kì trong tam giác. $M,N,P$ là hình chiếu của $K$ trên $BC,CA,AB$. $(MNP)$ cắt $BC$ tại $H$. $I,J$ là trung điểm của $BC,BA$. $IJ$ cắt $HN$ tại $L$. Chứng minh tam giác $LNP$ cân

Gọi $V$ là điểm đẳng giác với $K$ trong $\Delta ABC$.

Do $(MNP)$ là đường tròn Pedal ứng với điểm $K$ của $\Delta ABC$ nên $VH\perp BC$.

Gọi $T$ là điểm đối xứng với $N$ qua $L$.

Nhận thấy $IL|| NC$ và $L,I$ lần lượt là trụng điểm của $BC,TN$ nên $BT||AC$.

Từ đó ta có $BT\perp VN$. Ta có $\frac{BT}{BP}=\frac{BT}{CN}.\frac{CN}{BP}=\frac{BH}{CH}.\frac{CN}{BP}=\frac{VH.cot VBC}{VH.cotVCB}.\frac{KN.cotKCN}{KP.cotKBP}=\frac{KN}{KP}\Rightarrow \Delta KNP\sim\Delta BTP\Rightarrow TP\perp PN\Rightarrow PT\perp PN$.

Bài 6: Cho $\Delta ABC$ nhọn. Ba đường cao $AD,BE,CF$ cắt nhau tại $H$. $I$ là hình chiếu của $B$ trên $ED$. $J$ là trung điểm của $HD$  Chứng minh $F,J,D,I$ đồng viên.

$CH$ cắt $DE$ tại $K$.

Gọi $L$ là trung điểm của $CH$.

Áp dụng định lý Brocard cho tứ giác $DHEC$ nội tiếp ta có $BK\perp AL$.

$\Delta AHC\sim FHD(g.g)\Rightarrow \Delta ALC\sim FJD(c.g.c)\Rightarrow \angle ALC=\angle FJD$.

Mặt khác $BK\perp AL$ và $CF\perp BA$ nên $\angle ALC=180^o-\angle FBK$.

Mà tứ giác $BFKI$ nội tiếp nên $\angle FID=\angle FBK=180^o-\angle ALC=180^o-\angle FJD$.

Điều này dẫn đến $F,J,D,I$ đồng viên. (đpcm)

Bài 2: Cho tam giác ABC nhọn, các điểm $D,E,F$ lần lượt nằm trên các cạnh $BC,CA,AB$. Tìm vị trí của các điểm $D,E,F$ để chu vi tam giác $DEF$ nhỏ nhất.

Bài toán Fagnano - 1775:

Cách 2: Gọi $M,N$ lần lượt đối xứng với $D$ qua $AB,AC$. Khi đó $AM=AN=AD$ và $\angle MAN=2\angle BAC$.

Ta có $DE+EF+FD=EN+EF+FM\geq MN=2AM.\sin BAC=2AD.\sin BAC\geq 2h_a.\sin BAC$ với $h_a$ là đường cao xuất phát từ đỉnh $A$ của tam giác $ABC$.

Dấu bằng xảy ra khi $D,E,F$ là chân các đường cao của tam giác.

Bài đầu tiên trong năm 2022 

Bài 8: Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ có trực tâm $H$. $(BOC)$ cắt đường tròn đường kính $AO$ tại $P$, $(BHC)$ cắt đường tròn đường kính $AH$ ở $Q$. $AP$ cắt $(BOC)$ ở $I$, $AQ$ cắt $(BHC)$ ở $J$. Chứng minh $PQ//IJ$

Tổng quát điểm $H,O$ thành hai điểm liên hợp đẳng giác trong $\Delta ABC$.

Giả sử $AH$ nằm giữa $AO,AB$.

Dễ thấy $OI$ là đường kính của $(BOC)$ và $HJ$ là đường kính của $(BHC)$.

Theo định lý hàm số sin, ta có $OI=\frac{BC}{\sin \widehat{BOC}};HJ=\frac{BC}{\sin \widehat{BHC}}$.

Do đó $\frac{OI}{HJ}=\frac{\sin\widehat{BHC}}{\sin\widehat{BOC}}$.

Mặt khác: $\frac{AO}{AH}=\frac{AO}{CO}.\frac{CO}{BC}.\frac{BC}{BH}.\frac{BH}{AH}=\frac{\sin\widehat{OAC}}{\sin\widehat{OCA}}.\frac{\sin\widehat{OBC}}{\sin\widehat{BOC}}.\frac{\sin\widehat{BHC}}{\sin\widehat{HCB}}.\frac{\sin\widehat{BAH}}{\sin\widehat{ABH}}=\frac{\sin\widehat{BHC}}{\sin\widehat{BOC}}=\frac{OI}{HJ}$

$\Rightarrow \frac{OI}{HJ}=\frac{AO}{AH}$.

Mặt khác biến đổi góc ta có $\widehat{AHJ}-\widehat{AOI}=\widehat{AHC}+\widehat{JHC}-360^o+\widehat{AOC}+\widehat{IOC}=\widehat{AHC}+\widehat{AOC}-360^o+90^o-\widehat{HBC}+90^o-\widehat{OBC}=180^o-\widehat{HBC}-\widehat{OBC}+\widehat{BAC}+\widehat{ACB}=0^o\Rightarrow \widehat{AHJ}=\widehat{AOI}\Rightarrow \Delta AHJ\sim\Delta AOI(c.g.c)$.

Mà $HQ,OP$ là các đường cao tương ứng nên $\frac{AP}{AI}=\frac{AQ}{AJ}$ hay $PQ\parallel IJ$. (đpcm)

Bài tiếp theo

Bài 5: Cho tam giác $ABC$ ngoại tiếp đường tròn $(I)$, nội tiếp đường tròn $(O)$. Điểm Nagel là $R$. Kẻ $AX//BC$ với $X$ thuộc đường tròn $(O)$. $K$ là giao điểm của đường tròn đường kính $AI$ với $(O)$. Chứng minh: $\angle KAI=\angle AXR$

Cách khác:

$(I)$ tiếp xúc với $BC,CA,AB$ lần lượt tại $D,E,F$.

Vì $R$ là điểm Nagel nên $AR$ đi qua điểm tiếp xúc của đường tròn bàng tiếp góc $A$ $\Delta ABC$ với $BC$.

Do đó nếu kẻ đường kính $DV$ thì $V\in AR$.

Dễ thấy $AI$ đi qua điểm chính giữa $J$ của cung $BC$.

$\Delta KBF\sim\Delta KCE(g.g)\Rightarrow \frac{KB}{KC}=\frac{BF}{CE}=\frac{BD}{CD}\Rightarrow KD$ là phân giác góc $BKC$.

Từ đó $KD$ đi qua $J$.

Kẻ $RM\perp AX(M\in AX)$.

$DV$ cắt $AX$ tại $N$.

$BR$ cắt $AC$ tại $L$ thì $L,E$ đối xứng với nhau qua trung điểm của $AC$.

Áp dụng định lý Menelaus cho $\Delta AHC$ với cát tuyến $B,R,L$ ta có $\frac{RA}{RH}=\frac{BC}{BH}.\frac{LA}{LC}=\frac{BC}{LC}=\frac{2BC}{AB+AC-BC}\Rightarrow \frac{AR}{AH}=\frac{2BC}{AB+AC+BC}=\frac{2r}{h_{A}}=\frac{VH}{AH}\Rightarrow AR=VH$.

Do đó $\Delta ARM=\Delta HVD(g.c.g)$.

$OJ$ cắt $BC,AX$ lần lượt tại $P,Q$.

Khi đó $MX=AX-AM=AX-DH=2(AQ-DP)=2(AQ-NQ)=2AN$.

Mặt khác $\Delta KAN\sim\Delta KID(g.g)$ nên $\frac{KA}{KI}=\frac{AN}{ID}=\frac{MX}{MR}\Rightarrow \Delta KAI\sim\Delta MXR(c.g.c)\Rightarrow \angle KAI=\angle AXR$. (đpcm)

Bài 16: Cho $\Delta ABC$ nội tiếp $(O)$. $P$ bất kì trong $\Delta ABC$, đường thẳng qua $P$ vuông góc với $CA$, $AB$ cắt $BC$ tại $X$, $Y$. $(PBX)$ cắt $AB$ tại $Z$, $(PCY)$ cắt $CA$ tại $T$
a) Chứng minh $P$, $Z$, $T$ thẳng hàng
b) Tiếp tuyến tại $T$ của $(PCY)$ cắt tiếp tuyến tại $Z$ của $(PBX)$ tại $K$. Chứng minh $KA$ đi qua một trong 2 giao điểm của $(KZT)$ và $(O)$

b) Gọi (PCY) cắt lại (PBX) tại E.

Khi đó $\angle BEC=180^o-\angle EBC-\angle ECB=\angle EPX+\angle EPY-180^o=180^o-\angle XPY=\angle BAC\Rightarrow E\in (O)$.

Mặt khác $\angle TEZ=\angle ZEP-\angle TEP=180^o-\angle ABP-\angle ACP=180^o-\angle KZT-\angle KTZ=\angle ZKT$.

Do đó $Z,K,E,T$ đồng viên.

$(KZT)$ cắt $(O)$ lại tại $D$.

Khi đó $\angle KDE=\angle KZE=\angle ZPE-\angle TPE=\angle ACE=\angle ADE$.

Dẫn đến $A, K, D$ thẳng hàng hay ta có đpcm.

Kẻ đường kính $BG$ của $(T)$ thì $A,G,C$ thẳng hàng.

Lấy $K,I$ lần lượt là trung điểm của $AB,BC$.

Khi đó $I$ là giao hai tiếp tuyến tại $A,B$ của $(I)$.

Từ đó theo tính chất quen thuộc ta có $MK,MI$ đẳng giác trong $\angle AMB$.

Ta có $\angle AEC=\angle ADB=\angle BMK=\angle AMI=\angle AFC$.

Dẫn đến tứ giác $ACEF$ nội tiếp. Ta có đpcm.

Bài 15: Cho đường tròn $(O)$ đường kính $AB$. $C$ là một điểm thuộc đường tròn sao cho $CA>CB$. Kẻ $CH$ vuông góc với $AB$. Từ $H$ kẻ $HE,HF$ vuông góc với $CA,CB$. $(MOC)$ cắt $CH$ tại $K$. $EF$ cắt $(O)$ tại $M,N$ ($M$ thuộc cung nhỏ $CA$, $N$ thuộc cung nhỏ $CB$). Chứng minh rằng $KO$ và $HN$ cắt nhau tại một điểm $L$ trên $(O)$

Kẻ tiếp tuyến tại $C$ của $(O)$ cắt $HE,HF$ lần lượt tại $X,Y$.

Khi đó $H,X$ đối xứng với nhau qua $CA$; $H,Y$ đối xứng với nhau qua $CB$.

Lại có $EX.EH=EA.EC=EM.EN$ nên $X,M,H,N$ đồng viên.

Tương tự $Y,M,H,N$ đồng viên nên $X,Y,M,N,H$ đồng viên.

Mà $C$ là tâm của $(HXY)$ nên $CM=CN=CH$.

Giả sử $HN$ cắt lại $(O)$ tại $L$ thì do $C$ là tâm của $(HMN)$ nên $\frac{\angle MOL}{2}=\angle MNL=\angle MNH=\frac{\angle MCH}{2}=\frac{\angle MOK}{2}$.

Từ đó $O,K,L$ thẳng hàng nên ta có đpcm.

Tiếp theo là một bài giải trí vui vui, nhưng cũng khá hay!

Bài 11: Cho hình vẽ. Biết tam giác $ABC$ đều và đường tròn $(I)$ tiếp xúc với $BC$ như hình. Chứng minh: $BD+AE+AF=CD+AG+AH$

Gọi $J,K$ lần lượt là hình chiếu của $I$ trên $AB,AC$.

Khi đó $J,K$ lần lượt là trung điểm của $EF,GH$.

Ta có $AE+AF=2AJ;AH+AG=2AK$ nên ta quy về chứng minh $BD-CD=2(AK-AJ)$.

Ta có $BD-CD=\frac{BD^2-CD^2}{BD+CD}=\frac{BI^2-CI^2}{BC}=\frac{(BJ^2-CK^2)+(IJ^2-IK^2)}{BC}=\frac{(BJ-CK)(BJ+CK)+(AK^2-AJ^2)}{BC}=\frac{(AK-AJ)(BJ+CK)+(AK-AJ)(AK+AJ)}{BC}=\frac{(AK-AJ)(AB+AC)}{BC}=2(AK-AJ)$ hay ta có đpcm.

Bài 10: Cho dây cung $BC$ trên $(O)$. $A$ di chuyển trên cung lớn $BC$. $E,F$ đối xứng với $B,C$ qua $AC,AB$. $I$ là trung điểm của $EF$. Chứng minh $AI$ đi qua một điểm cố định

$BE,CF$ lần lượt cắt $AC,AB$ tại $X,Y$.

Khi đó $BX$ cắt $CY$ tại trực tâm $H$ của $\Delta ABC$.

Gọi $M,K,J$ theo thứ tự là trung điểm của $BC,XY,AH$. 

$AI$ cắt $OM$ tại $D$. Ta sẽ chứng minh $D$ cố định.

Nhận thấy $IX,IY$ lần lượt là đường trung bình của các tam giác $EBF,ECF$ nên $IX=\frac{BF}{2}=\frac{BC}{2}=\frac{CE}{2}=IY$.

Suy ra $M,K,J,I$ cùng thuộc đường trung trực của $XY$.

Ta cũng có $MX=MY=\frac{BC}{2}=IX=IY$ nên $I,M$ đối xứng với nhau qua $XY$.

Ta có $\frac{KJ}{KM}=\frac{YJ^2}{MY^2}=\frac{AH^2}{BC^2}=\frac{4OM^2}{BC^2}$ luôn không đổi nên tỉ số $\frac{MK}{MJ}$ không đổi $\Rightarrow \frac{MJ}{MI}$ không đổi $\Rightarrow \frac{IJ}{IM}$ không đổi hay $\frac{AJ}{DM}$ không đổi.

Mà $AJ=OM$ không đổi nên độ dài $DM$ không đổi.

Vậy $AI$ đi qua $D$ cố định.

Xin góp một số câu cho TOPIC:

Bài 2: Cho tam giác ABC nhọn, các điểm $D,E,F$ lần lượt nằm trên các cạnh $BC,CA,AB$. Tìm vị trí của các điểm $D,E,F$ để chu vi tam giác $DEF$ nhỏ nhất.

Bài 3: Cho điểm $P$ nằm ngoài đường tròn $(O)$. Từ $P$ kẻ tiếp tuyến $PA, PB$ tới $(O)$. $M$ là điểm bất kì di chuyển trên cung lớn $AB$. Gọi $T$ là trung điểm của $AB$. Góc $\widehat{xTy}=90^o$ quay quanh điểm $T$ sao cho $Tx$ cắt đoạn thẳng $MA$ tại $E$, $Ty$ cắt đoạn thẳng $MB$ tại $F$. Chứng minh rằng độ lớn của góc $\widehat{EPF}$ không phụ thuộc vào vị trí điểm $M$ và góc $\widehat{xTy}$.

Bài 1: Cho $\Delta ABC$ nhọn ($AB<AC$) nội tiếp đường tròn $(O)$. $X$ là chân đường cao hạ từ $A$ xuống $BC$, $Y$ là một điểm di động trên $AX$. Đường tròn tâm $Z$ đường kính $AY$ cắt $AC,AB$ tại $I,J$. Đường tròn $(AIJ)$ cắt $(O)$ tại $L$. $K$ là giao điểm của $BI$ và $CJ$. Chứng minh $L,Y,K$ thẳng hàng

Bổ đề: Cho ba đường tròn $(O_1),(O_2),(O_3)$ đôi một cắt nhau. Gọi $(O_1)\cap (O_2)=\{A,B\};(O_2)\cap (O_3)=\{C,D\};(O_3)\cap (O_1)=\{E,F\}$. Khi đó $AB,CD,EF$ đồng quy hoặc đôi một song song.

Chứng minh: Nếu $AB\parallel CD$ thì do $O_1O2\perp AB$ và $O_2O_3\perp CD$ nên $O_1,O_2,O_3$ thẳng hàng. Suy ra $AB\parallel CD\parallel EF$.

Nếu $AB$ cắt $CD$ tại M thì gọi $ME$ cắt $(O_3)$ lại tại $F'$. Ta có $ME.MF'=MC.MD$ và $MC.MD=MA.MB$ nên $ME.MF'=MA.MB$ suy ra $F'$ thuộc đường tròn $(O_1)$ nên $F'$ là giao điểm khác $E$ của $(O_1)$ và $(O_3)$. Từ đó $F'\equiv F$ hay $AB,CD,EF$ đồng quy.

Quay trở lại bài toán:

Do $\angle BJY=\angle BXY=90^\circ$ nên tứ giác $BJYX$ nội tiếp. Tương tự tứ giác $CIYX$ nội tiếp $\Rightarrow AJ.AB=AY.AX=AI.AC$ nên tứ giác $BJIC$ nội tiếp. Gọi $T$ là tâm đường tròn ngoại tiếp tứ giác này

Xét ba đường tròn $(AIJ),(T),(O)$ thì theo bổ đề, ta có $AL,IJ,BC$ đồng quy tại $E$.

Gọi $F$ là giao của $(KIJ)$ và $(KBC)$ ($F\neq K$) thì theo bổ đề ta cũng có $E\in KF$.

Ta có $\angle IFC=360^o-\angle IFK-\angle KFC=\angle IJC+\angle IBC=\angle ITC$ suy ra tứ giác $IFTC$ nội tiếp.

Tương tự tứ giác $(JFTB)$ nội tiếp. Áp dụng bổ đề cho ba đường tròn $(ITC),(JTB),(T)$ ta có $A,F,T$ thẳng hàng.

Do đó $\angle AFK=\angle IFK-\angle IFA=180^o-\angle IJC-\angle ICT=90^o$.

Mặt khác $EK.EF=EL.EA$ nên tứ giác $ALKF$ nội tiếp.

Dẫn đến $\angle ALK=90^o$ hay $L,Y,K$ thẳng hàng.

Bài 8: Cho các số thực dương x, y, z thỏa mãn x + y + z = 1. Chứng minh rằng: $\sum_{cyc}\frac{xy}{x^2+y^2}+\frac{1}{4}(\sum_{cyc}\frac{1}{x})\geqslant \frac{15}{4}$

$BĐT\Leftrightarrow \frac{1}{4}(x+y+z)(\frac{1}{x}+\frac{1}{y}+\frac{1}{z})+\sum\frac{xy}{x^2+y^2}\geq \frac{15}{4}$

$\Leftrightarrow \frac{1}{4}\sum(\frac{x}{y}+\frac{y}{x}-2)\geq \sum(\frac{1}{2}-\frac{xy}{x^2+y^2})$

$\Leftrightarrow \sum\frac{(x-y)^2}{4xy}\geq\sum\frac{(x-y)^2}{2(x^2+y^2)}$.

Dễ thấy bđt trên luôn đúng. Ta có đpcm.

Bài 4: Với các số thực dương a, b thay đổi. Chứng minh rằng: $(a+b)(\frac{1}{\sqrt{a^2-ab+2b^2}}+\frac{1}{\sqrt{b^2-ab+2a^2}})\leqslant 2\sqrt{2}$ (Chú ý: Bài 4 không được dùng tất cả các bất đẳng thức đã có như Cô-si, Cauchy-Schwarz, Cauchy-Schwarz dạng phân thức,...)

Chuẩn hoá $a+b=2$. Ta có $\frac{1}{\sqrt{a^2-ab+2b^2}}=\frac{1}{\sqrt{4a^2-10a+8}}$.

Ta chứng minh: $\frac{1}{\sqrt{4a^2-10a+8}}\leq \frac{\sqrt{2}}{4}a+\frac{\sqrt{2}}{4}$. (*)

Thật vậy, $(*)\Leftrightarrow 2a(a-1)^2(2a+3)\leq 0$ (luôn đúng)

Tương tự, $\frac{1}{\sqrt{b^2-ab+2a^2}}=\frac{1}{\sqrt{4b^2-10b+8}}\leq \frac{\sqrt{2}}{4}b+\frac{\sqrt{2}}{4}$.

Cộng vế với vế ta có đpcm.

Bài 7: Cho các số a, b, c thỏa mãn $0<a,b,c\leqslant 1$. Chứng minh rằng: $\sum \frac{1}{a+b}\geqslant \sum \frac{6}{11+a^3}$ 

Không biết có đúng không:

Ta có $\frac{6}{11+a^3}+\frac{1}{8}a-\frac{5}{8}=\frac{(a-1)^2(a^2-3a-7)}{8(a^3+11)}\leq 0\Rightarrow \frac{6}{11+a^3}\leq \frac{-1}{8}a+\frac{5}{8}$.

Tương tự với b, c rồi cộng vế với vế ta được $\sum\frac{6}{11+a^3}\leq \frac{-1}{8}(a+b+c)+\frac{15}{8}$. (1)

Ta thấy với $x\in(0;2]$ thì $\frac{1}{x}+\frac{1}{16}x-\frac{5}{8}=\frac{(x-8)(x-2)}{16x}\geq 0\Rightarrow \frac{1}{x}\geq \frac{-1}{16}x+\frac{5}{8}$.

Thay x bằng a + b, b + c, c + a rồi cộng vế với vế ta có $\sum\frac{1}{a+b}\geq \frac{-1}{8}(a+b+c)+\frac{15}{8}$. (2)

Từ (1), (2) có đpcm.

Bài 2: Cho a, b, c là các số thực thỏa mãn $ab+bc+ca\geqslant 0 $. Chứng minh rằng: $(a+b+c)(\frac{3a-b}{a^2+ab}+\frac{3b-c}{b^2+bc}+\frac{3c-a}{c^2+ca})\leqslant 9$

Phản ví dụ: a = 5; b = 7; c = -2.

Bài 10: Cho a, b, c không âm và $a^2+b^2+c^2=3$. Tìm GTLN của: $P=\frac{a}{b+2}+\frac{b}{c+2}+\frac{c}{a+2}$

Ta chứng minh $P\leq 1$ (1).  Thật vậy bằng biến đổi tương đương ta có $(1)\Leftrightarrow ab^2+bc^2+ca^2-abc\leq 2$.

Giả sử c = mid{a, b, c}. Khi đó $b(c-a)(c-b)\leq 0$ nên $ab^2+bc^2\leq abc+b^2c$.

Từ đó $ab^2+bc^2+ca^2-abc\leq ca^2+b^2c=c(3-c^2)=2-(c-1)^2(c+2)\leq 2$.

Vậy ta có đpcm.

Bài 17: Cho $a,b,c\geqslant 0$ thỏa mãn $ab+bc+ca+abc=4$. Chứng minh rằng: $3(a^2+b^2+c^2)+abc\geqslant 10$ 

Bất đẳng thức này không chặt lắm nên chắc chưa cần dùng đến pqr:

Ta có $3(a^2+b^2+c^2)+abc=3(a^2+b^2+c^2)+4-(ab+bc+ca)\geq 2(a^2+b^2+c^2)+4\geq 2.3+4=10$.

Bài 42: Chứng minh rằng: $a(a+b)(a^2+b^2)(a^4+b^4)+b(b+c)(b^2+c^2)(b^4+c^4)+c(c+a)(c^2+a^2)(c^4+a^4)\geqslant 0$

Đặt A = $\sum_{cyc}a(a+b)(a^2+b^2)(a^4+b^4)$. B = $\sum_{cyc}b(a+b)(a^2+b^2)(a^4+b^4)$.

Dễ thấy A - B = 0 nên A = B.

Mặt khác do A + B = $\sum(a+b)^2(a^2+b^2)(a^4+b^4)\geq 0$ nên $A\geq 0$.

Dấu "=" xảy ra khi a = b = c = 0.

Bài 40: Cho $a,b,c,d,e>0$ thỏa mãn $\sum_{cyc}\frac{1}{4+a}=1$. Chứng minh rằng: $\sum_{cyc}\frac{a}{4+a^2}\leqslant 1$

Ta có $\sum\frac{1}{4+a}=1\Leftrightarrow \sum\frac{a-1}{a+4}=0$.

BĐT tương đương: $\sum \frac{(a-1)(a-4)}{a^2+4}\geq 0\Leftrightarrow \sum(\frac{a-1}{a+4}.\frac{a^2-16}{a^2+4})\geq 0$.

Bất đẳng thức trên đúng theo Chevbyshev do $\frac{a-1}{a+4}\geq \frac{b-1}{b+4}\Leftrightarrow \frac{a^2-16}{a^4+4}\geq\frac{b^2-16}{b^2+4}$.

Bài 36: Chứng minh rằng với $a,b,c$ dương thì: $\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}\geqslant \frac{3}{2}$ (Bất đẳng thức Nesbitt)

Áp dụng bất đẳng thức Chevbyshev cho hai bộ số đơn điệu cùng chiều $(a,b,c);(\frac{1}{b+c},\frac{1}{c+a},\frac{1}{a+b})$ ta có:

$\sum\frac{a}{b+c}\geq \frac{1}{3}(a+b+c)(\sum\frac{1}{a+b})\geq \frac{3}{2}$

Bài 18: Tìm hằng số k tốt nhất sao cho bất đẳng thức sau đúng với mọi số thực không âm $a,b,c$ thỏa mãn $ab+bc+ca+abc=4$; $a^2+b^2+c^2+kabc\geqslant k+3$

Với a = 0; b = c = 2 ta có $5\geq k$.

Với $k=5$ ta có bất đẳng thức $a^2+b^2+c^2+5abc\geq 8$. Bất đẳng thức này đã có lời giải ở Marathon: (Mình lấy lời giải của anh 12DecMath).

Vậy hằng số k tốt nhất là 5.

Bài 1: Cho a, b, c là các số thực dương thỏa mãn $abc=\frac{3}{2}$. Chứng minh rằng: $\frac{ab}{a+b}+\frac{bc}{b+c}+\frac{ca}{c+a}\geqslant \frac{a+b+c}{a^3+b^3+c^3}$

Mình nghĩ $abc=\frac{2}{3}$ thì đúng hơn chứ nhỉ?

Ta có $\sum\frac{ab}{a+b}=\frac{2}{3}\sum\frac{1}{ac+bc}\geq \frac{3}{ab+bc+ca}$ nên ta chỉ cần chứng minh $3(a^3+b^3+c^3)\geq (a+b+c)(ab+bc+ca)$.

Mặt khác dễ dàng có $3(a^3+b^3+c^3)\geq (a^2+b^2+c^2)(a+b+c)\geq (a+b+c)(ab+bc+ca)$ nên ta có đpcm.