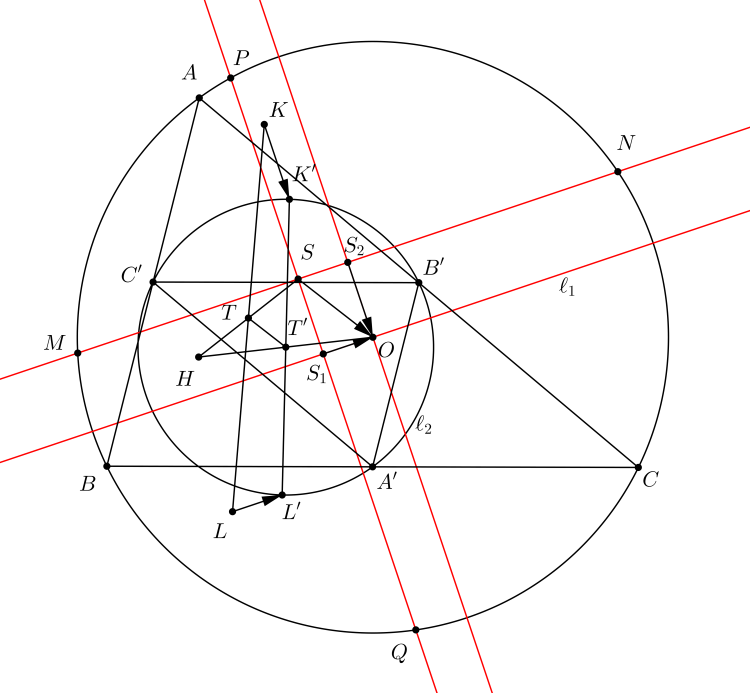
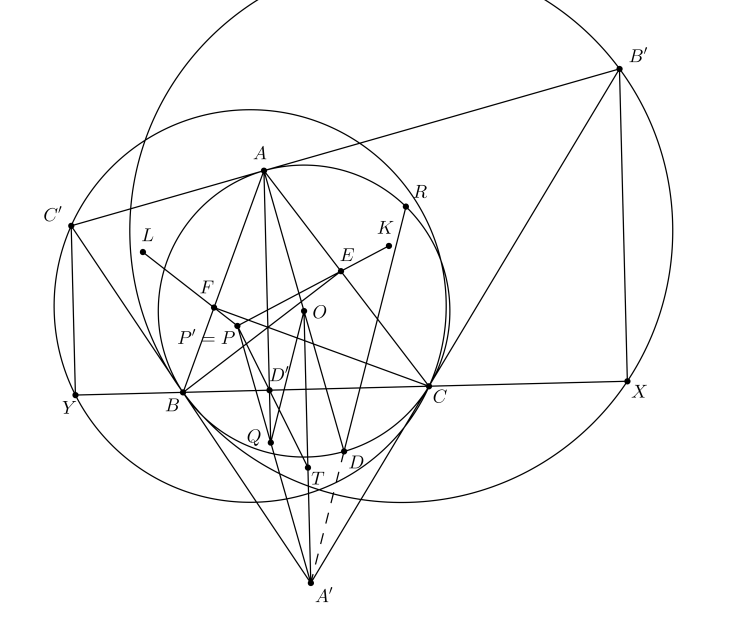
Lời giải của Trung đúng rồi.

Bài 2 mình tìm ra đã rất lâu. Ban đầu mình tìm ra với trường hợp $X\equiv D$, $Y\equiv E$, $Z\equiv F$ rồi tổng quát lên. Chứng minh của mình cũng biến đổi góc thôi.

Bài 2 là một bài rất nhẹ nhàng.

Mình mong đợi nhiều hơn chỉ là một lời giải - không phải vì mình chờ lời giải khác mà là vì cấu hình bài toán còn nhiều thứ để vọc lắm. Bài toán không phải để giải.

Mình hoàn thiện chứng minh trên của Min Nq bằng hình học định hướng

$2\overrightarrow{QP}=\overrightarrow{KX}+\overrightarrow{HZ}$, mà $KX=HZ$ nên $(\overrightarrow{QP},\overrightarrow{KX})=(\overrightarrow{HZ},\overrightarrow{KX})$ 

Góc giữa hai vector là góc định hướng $(\mod 2\pi)$

$\Rightarrow 2(\overrightarrow{QP},\overrightarrow{HZ})=(\overrightarrow{KX},\overrightarrow{HZ})=(\overrightarrow{KX},\overrightarrow{MO})+(\overrightarrow{MO},\overrightarrow{HZ})=2(\overrightarrow{BC},\overrightarrow{MO})+2(\overrightarrow{MO},\overrightarrow{AD})$

$\Rightarrow 2(\overrightarrow{QP},\overrightarrow{MO})=2(\overrightarrow{BC},\overrightarrow{AD})+2(\overrightarrow{HZ},\overrightarrow{MO})=2(\overrightarrow{BC},\overrightarrow{AD})+4(\overrightarrow{AD},\overrightarrow{MO})=2(\overrightarrow{BC},\overrightarrow{MO})+2(\overrightarrow{AD},\overrightarrow{MO})$

Đến đây chia hai vế cho 2(chia hai vế thì phải chia cả số chia)

$\Rightarrow (QP,MO)=(BC,MO)+(AD,MO)\pmod\pi$

Hơn nữa chú ý rằng $(BC,MO)+(AD,MO)=(AC,MO)+(BD,MO)=(AB,MO)+(CD,MO)\pmod\pi$ nên 4 điểm thẳng hàng.

Em mạo hiểm đề nghị bài sau

Bài toán 158. (Quan sát từ lâu) Cho 4 điểm phân biệt $A$, $B$, $C$, $D$ đồng viên. $M$ bất kì. $P_{ab}$ đối xứng với $M$ qua $AB.$

Tương tự ta xác định các điểm $P_{bc}$, $P_{ca}$, $P_{da}$, $P_{db}$, $P_{dc}.$

Chứng minh rằng đường thẳng đi qua trung điểm $P_{da}P_{bc}$, $P_{ca}P_{db}$, $P_{ab}P_{dc}$ quay quanh một điểm cố định khi $M$ di động.

___________________________________________

P/S: Khi $M$ chạy ta còn thu được nhiều bất biến, quỹ tích, hình bao hay ho khác.

Bạn Min Nq làm đúng rồi. Bài 156 chỉ cần định lý Menelaus nhưng mình trình bày như sau:

$\triangle DBC\sim\triangle AEC\sim\triangle ABF\sim\triangle A'B'C'\text{ nào đó}$

Đường thẳng Euler của $\triangle A'B'C'$ cắt $B'C'$, $C'A'$, $A'B'$ tại $D'$, $E'$, $F'$ thì

\[\frac{\overline{XB}}{\overline{XC}}\cdot\frac{\overline{YC}}{\overline{YA}}\cdot\frac{\overline{ZA}}{\overline{ZB}}=\frac{\overline{D'B'}}{\overline{D'C'}}\cdot\frac{\overline{E'C'}}{\overline{E'A'}}\cdot\frac{\overline{F'A'}}{\overline{F'B'}}=1\]

Vậy $X$, $Y$, $Z$ thẳng hàng.

Thực ra không cần tới đường thẳng Euler, chỉ cần thay bởi các đường thẳng $\ell_a$, $\ell_b$, $\ell_c$ thỏa mãn

\[\triangle DBC\cup\ell_a\sim\triangle AEC\cup\ell_b\sim\triangle ABF\cup\ell_c\]

Lời giải bài toán 155.

Em sẽ tính toán.

Đặt $a=BC$, $b=CA$, $c=AB$, và $p=\dfrac{a+b+c}{2}$

Vì $K$, $L$, $E$, $N$ đồng viên nên $CK\cdot CL=CE\cdot CN$

Chỉ cần tính được $CN$ - tức là biểu diễn được $CN$ qua $a$, $b$, $c$.

\[CK\cdot CL=CK^2+KL\cdot KC=CK^2+KD\cdot KF\]

Theo công thức tính độ dài đường phân giác, công thức hạ bậc và định lý cos

\[CK=\dfrac{2ab\cos\frac{C}{2}}{a+b}\Rightarrow CK^2=\frac{4a^2b^2\cos^2\dfrac{C}{2}}{(a+b)^2}=\frac{2a^2b^2(1+\cos C)}{(a+b)^2}=\frac{ab(a+b+c)(a+b-c)}{(a+b)^2}\]

\[KD=|AD-AK|=|p-a-\frac{bc}{a+b}|=|\frac{(a-b)(a+b-c)}{2(a+b)}|\]

\[KF=|AF-AK|=|p-b-\frac{bc}{a+b}|=|\frac{(a-b)(a+b+c)}{2(a+b)}|\]

\[\Rightarrow CK^2+KD\cdot KF=\frac{(a+b-c)(a+b+c)}{4(a+b)^2}\Big{(}(a-b)^2+4ab\Big{)}=\frac{(a+b+c)(a+b-c)}{4}=p(p-c)\]

Mà $CE=p-c$ nên $CN=p$ $\Rightarrow$ $BN=p-a=BF$.

Vậy $\triangle BNF$ cân tại $B$.

Lời giải bài toán 154.

Định lý. $A'$, $B'$, $C'$ lần lượt là trung điểm $BC$, $CA$, $AB$ thì tâm đẳng phương của ba đường tròn bàng tiếp là tâm đường tròn nội tiếp của $\triangle A'B'C'$.

Chứng minh định lý. Ta chỉ cần chứng minh đường phân giác của $\angle B'A'C'$ là trục đẳng phương của đường tròn bàng tiếp góc $B$ và $C$.

Gọi $(I_b)$, $(I_c)$ là đường tròn bàng tiếp góc $B$ và $C$.

$(I_b)$, $(I_c)$ tiếp xúc $BC$ tại $M$, $N$.

Nhớ lại rằng $BN=CM=p-a$, trong đó $a=BC$, $b=CA$, $c=AB$ và $p=\dfrac{a+b+c}{2}$

nên $A'$ là trung điểm $MN$, suy ra $A'$ thuộc trục đẳng phương của $(I_b)$ và $(I_c)$. Hơn nữa phân giác của $\angle B'A'C'$ song song với $AI_a$ nên cũng vuông góc với $I_bI_c$ (đường nối tâm) nên nó chính là trục đẳng phương của $(I_b)$ và $(I_c)$.

Quay trở lại bài toán

Gọi $S$, $G$, $N$ là tâm đẳng phương của ba đường tròn bàng tiếp, trọng tâm, tâm đường tròn chín điểm.

Ta có $\overrightarrow{IS}=\dfrac{3}{2}\cdot\overrightarrow{IG}$ nên ta cần chỉ ra $G$ chạy trên đường tròn cố định.

Thế nhưng lại có $\overrightarrow{OG}=\dfrac{2}{3}\overrightarrow{ON}$ nên ta cần chỉ ra $N$ chạy trên đường tròn cố định - điều này lại là hiển nhiên vì $IN=\dfrac{R}{2}-r$ nên $N$ chạy trên đường tròn cố định.

Vậy $S$ chạy trên đường tròn cố định.

____________________________________________

$\boxed{\text{Bài toán 156}}$(quan sát và đã chứng minh) Cho $\triangle ABC$ và điểm $P$ bất kì. $PA$, $PB$, $PC$ lần lượt cắt $(PBC)$, $(PCA)$, $(PAB)$ tại $D$, $E$, $F$.

Đường thẳng Euler của $\triangle DBC$ cắt $BC$ tại $X$.

Đường thẳng Euler của $\triangle ECA$ cắt $CA$ tại $Y$.

Đường thẳng Euler của $\triangle FAB$ cắt $AB$ tại $Z$.

Chứng minh rằng $X$, $Y$, $Z$ thẳng hàng.

Lời giải cho bài 148

Em sẽ phát biểu lại bài toán như sau:

\[(PB,PC)+(PE,PF)=0\pmod\pi \Leftrightarrow (QB,QC)+(QE,QF)=0\pmod\pi\]

Gọi $P_a$, $P_b$, $P_c$, $P'$ là hình chiếu vuông góc của $P$ lên $BC$, $CA$, $AB$, $EF$

 và $Q_a$, $Q_b$, $Q_c$, $Q'$ là hình chiếu vuông góc của $Q$ lên $BC$, $CA$, $AB$, $EF$.

 

\[(Q'Q_b,Q'Q_c)=(Q'Q_b,Q'E)+(Q'F,Q'Q_c)=(QQ_b,QE)+(QF,QQ_c)=(QF,QE)+(AC,AB)\pmod\pi\]

\[\Rightarrow (Q'Q_b,Q'Q_c)-(Q_aQ_b,Q_aQ_c)=(QF,QE)+(AC,AB)+(PB,PC)=(QF,QE)+(QC,QB)\pmod\pi\]

Vậy $(QB,QC)+(QE,QF)=0\pmod\pi$ khi và chỉ khi $Q'$ thuộc đường tròn pedal của $P$, $Q$

Tương tự, $(PB,PC)+(PE,PF)=0\pmod\pi$ khi và chỉ khi $P'$ thuộc đường tròn pedal của $P$, $Q$.

$O$ là trung điểm $PQ$, theo tính chất hình thang vuông thì $OP=OQ$ nên $Q'$ thuộc đường tròn pedal của $P,Q$ khi và chỉ khi $P'$ thuộc đường tròn pedal của $P,Q$. Chứng minh hoàn tất.

Em đề nghị bài toán mới

$\boxed{\text{Bài toán 149}}$(tự chế và đã chứng minh không tọa độ) Cho $\triangle ABC$ và điểm $P$ bất kì.

$A_b$, $A_c$ là hình chiếu vuông góc của $A$ lên $PB$, $PC$

$B_c$, $B_a$ là hình chiếu vuông góc của $B$ lên $PC$, $PA$

$C_a$, $C_b$ là hình chiếu vuông góc của $C$ lên $PA$, $PB$

$C_aA_c$ cắt $A_bB_a$ tại $A_1$, $A_bB_a$ cắt $B_cC_b$ tại $B_1$, $B_cC_b$ cắt $C_aA_c$ tại $C_1$

$B_cB_a$ cắt $C_aC_b$ tại $A_2$, $C_aC_b$ cắt $A_bA_c$ tại $B_2$, $A_bA_c$ cắt $B_cB_a$ tại $C_2$

Chứng minh rằng $AA_1$, $BB_1$, $CC_1$ đồng quy khi và chỉ khi $AA_2$, $BB_2$, $CC_2$ đồng quy.

 

 

Thực ra bài 145 không cần dùng đến lượng giác.

Bài 145 là sự kết hợp của hai tính chất:

Tính chất 1. $O_a$, $O_b$, $O_c$ là tâm đường tròn ngoại tiếp của $\triangle OBC$, $\triangle OCA$, $\triangle OAB$ thì $AO_a$, $BO_b$, $CO_c$ đồng quy tại điểm đẳng giác của tâm đường tròn chín điểm của $\triangle ABC$.

Tính chất 2. $N$ là tâm đường tròn chín điểm của $\triangle ABC$. $D$, $E$, $F$ là hình chiếu vuông góc của $N$ lên $BC$, $CA$, $AB$. $X$, $Y$, $Z$ đối xứng với $A$, $B$, $C$ qua $BC$, $CA$, $AB$ thì $\triangle DEF$ và $\triangle XYZ$ vị tự.

___________________________________________

Chứng minh tính chất 1. Gọi $D$, $E$, $F$ là đối xứng của $O$ qua trung điểm $BC$, $CA$, $AB$ (thì cũng là đối xứng qua $BC$, $CA$, $AB$). Khi đó theo tính chất $\dfrac{2}{3}$ của trọng tâm, $AD$, $BE$, $CF$ đồng quy tại tâm đường tròn chín điểm $N$ (bởi vì $\overrightarrow{OG}+2\overrightarrow{NG}=\overrightarrow{0}$)

$T_a$, $A'$ là giao điểm hai tiếp tuyến tại $B$, $C$ của $(ABC)$, trung điểm $BC$. Trung trực của $BC$ cắt $(ABC)$ tại $A_1$, $A_2$.

\[R^2=\overline{OA_1}^2=\overline{OA_2}^2=\overline{OA'}\cdot\overline{OT_a}=\frac{\overline{OD}}{2}\cdot 2\overline{OO_a}=\overline{OD}\cdot\overline{OO_a}\]

Đẳng thức trên cho thấy $(A_1,A_2;O_a,D)=-1$. Mà $AA_1\perp AA_2$ nên $AO_a$, $AD$ đối xứng nhau qua phân giác $\angle BAC$. Tương tự với $AO_a$, $BO_b$, $CO_c$ ta suy ra chúng đồng quy tại điểm đẳng giác của $N$.

Chứng minh tính chất 2.

$H$, $N$, $G$, $O$ lần lượt là trực tâm, tâm đường tròn chín điểm, trọng tâm và tâm ngoại tiếp của $\triangle ABC$.

$A_1$ đối xứng với $N$ qua $BC$, $A_2$ đối xứng với $O$ qua $BC$.

$A$, $N$, $A_2$ thẳng hàng, đối xứng qua $BC$ suy ra $X$, $A_1$, $O$ thẳng hàng. Theo định lý đường trung bình, $\overrightarrow{HX}=2\overrightarrow{NA_1}=4\overrightarrow{ND}$

Tương tự, $\overrightarrow{HY}=4\overrightarrow{NE}$ và $\overrightarrow{HZ}=4\overrightarrow{NF}$ nên $\triangle DEF\cup N$ vị tự với $\triangle XYZ\cup H$.

Hơn nữa, tâm vị tự chính là $G$ vì tỉ số vị tự là $\dfrac{1}{4}$.

Em đăng lời giải cho bài 143.
$O_a$ là tâm ngoại tiếp tam giác $AA_1A_2$.
Như vậy $AO_a$ và đường thẳng qua $A$ và song song $BC$ đẳng giác với góc $BAC$. Vậy $AO_a$ là tiếp tuyến của $(ABC)$ nên $(O)$ trực giao với $(AA_1A_2)$. Tương tự $(O)$ trực giao với $(BB_1B_2)$ và $(CC_1C_2)$. Do đó $(K)$ và $(L)$ là nghịch đảo của nhau qua phép nghịch đảo đường tròn $(O)$, điều đó dẫn đến $(O)$, $(K)$, $(L)$ đồng trục.

Đây là đường tròn Hervey và em thấy nó khó tiếp cận nên em sẽ sử dụng tọa độ Oxy.

Cũng vì lời giải sau sử dụng tọa độ(cùng với vài kiến thức không phổ thông) nên em sẽ không đề xuất bài mới ạ.

_________________________________________________

Ý tưởng về cách chọn tọa độ: Với bài toán này, ta KHÔNG NÊN lấy 4 đường thẳng bất kì vì như vậy sẽ không có một quy luật nào và biến đổi đại số sẽ mất đi phần đẹp đẽ. Để xây dựng cách chọn, ta dựa trên một số tính chất của tứ giác toàn phần như sau.

Tính chất 1(tham khảo tại Epsilon 11 - Điểm Steiner. Điểm Anti-Steiner). Tồn tại duy nhất một parabola tiếp xúc với 4 đường thẳng của một tứ giác toàn phần cho trước và đường thẳng Steiner cũng chính là đường chuẩn của parabola này.

 

Như vậy đã rõ, ta sẽ lấy một đường parabola và chọn lấy 4 tiếp tuyến bất kì của nó - như vậy là đã bao quát được mọi trường hợp ! Tuy nhiên vì mọi parabola đều đồng dạng nên ta chỉ cần chọn parabola có phương trình $y=x^2$. Tiếp tuyến của parabola này tại điểm $(m,m^2)$ có phương trình $y=2mx-m^2$

Ta chọn ra 4 tiếp tuyến:

\[y=2x_1x-x_1^2\qquad y=2x_2x-x_2^2\qquad y=2x_3x-x_3^2\qquad y=2x_4x-x_4^2\]

Tính chất 2(http://forumgeom.fau...00406index.html) Với tứ giác toàn phần $(\ell_1,\ell_2,\ell_3,\ell_4)$, cực trực giao của $\ell_1$ với tam giác tạo bởi $(\ell_2,\ell_3,\ell_4)$ thuộc đường thẳng Steiner của tứ giác toàn phần đó.

_________________________________________________

Bắt đầu tính toán

Thay vì dẫn ra trực tiếp những tính toán thủ công, ta chỉ đưa ra các kết quả, công thức được sử dụng và nếu ra nó được dùng như thế nào.

Nhắc lại định nghĩa cực trực giao của $\ell$ với tam giác $ABC$: $D$, $E$, $F$ là hình chiếu vuông góc của $A$, $B$, $C$ lên $\ell$ thì đường thẳng qua $D$, $E$, $F$ và lần lượt vuông góc với $BC$, $CA$, $AB$ đồng quy tại cực trực giao của $\ell$ với tam giác $ABC$.

Như vậy ta sẽ cần tới công thức hình chiếu vuông góc.

Định lý 1(tọa độ hình chiếu vuông góc). Hình chiếu vuông góc của điểm $(x_0,y_0)$ lên đường thẳng $ax+by+c=0$ có tọa độ là

\[\Bigl{(}x_0-\frac{a(ax_0+by_0+c)}{a^2+b^2},y_0-\frac{b(ax_0+by_0+c)}{a^2+b^2}\Bigl{)}\]

 

Giao điểm của $\ell_1$ với $\ell_2$ là điểm $\Bigl{(}\dfrac{x_1+x_2}{2},x_1x_2\Bigl{)}$. Tương tự, ta có được tọa độ các đỉnh khác của tứ giác toàn phần. Qua một lượng các bước tính, ta thu được tọa độ của cực trực giao $P_1$ là

\[\Bigl{(}2x_2x_3x_4+\frac{x_2+x_3+x_4}{2}+\frac{2(x_1-x_2)(x_1-x_3)(x_1-x_4)}{1+4x_1^2},\frac{-1}{4}\Bigl{)}\]

Tiếp tục, ta tính được tọa độ của $X_1$ là

\[\Bigl{(}2x_2x_3x_4+\frac{x_2+x_3+x_4}{2}+\frac{2(x_1-x_2)(x_1-x_3)(x_1-x_4)}{1+4x_1^2},\]

\[4x_1x_2x_3x_4+x_1(-x_1+x_2+x_3+x_4)+\frac{4x_1(x_1-x_2)(x_1-x_3)(x_1-x_4)}{1+4x_1^2}\Bigl{)}\]

Tương tự, ta cũng thu được tọa độ của $X_2$, $X_3$ và $X_4$ vì sự bình đẳng của 4 cạnh của tứ giác toàn phần.

Bước cuối cùng là khó nhất, ta cần chứng minh 4 điểm trên đồng viên. Đây là một công việc có khối lượng tính toán hết sức khủng khiếp cho nên ta chỉ chứng minh một kết quả trung gian

_______________________________________________

Trong Oxy, cho 4 điểm $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$, $(x_4,y_4)$ mà 3 điểm bất kì trong số chúng đều không thẳng hảng. Câu hỏi đặt ra là tìm điều kiện để 4 điểm này đồng viên.

Vì $(x_1,y_1)$, $(x_2,y_2)$, $(x_3,y_3)$ không thẳng hàng nên sẽ có một đường tròn đi qua chúng, với phương trình có dạng $x^2+y^2+ax+by+c=0$. Điều kiện cần và đủ để 4 điểm đồng viên là tọa độ của cả 4 điểm phải thỏa mãn phương trình đó, tức là

\[(x_1^2+y_1^2)+ax_1+by_1+c=0\]

\[(x_2^2+y_2^2)+ax_2+by_2+c=0\]

\[(x_3^2+y_3^2)+ax_3+by_3+c=0\]

\[(x_4^2+y_4^2)+ax_4+by_4+c=0\]

Hệ nếu chỉ gồm 3 phương trình đầu thì chắc chắn có nghiệm $(a,b,c)$ nhưng nếu bổ sung phương trình thứ 4 thì chưa chắc. Vì vậy, để hệ 4 phương trình này có nghiệm thì phương trình thứ 4 phải là tổ hợp tuyến tính của 3 phương trình còn lại. Nói cách khác thì ta phải có định thức $4\times 4$ với 4 hàng  là $(1,1,1,1)$, $(x_1,x_2,x_3,x_4)$, $(y_1,y_2,y_3,y_4)$, $(x_1^2+y_1^2,x_2^2+y_2^2,x_3^2+y_3^2,x_4^2+y_4^2)$ phải bằng 0.

_______________________________________________

Chốt lại, "lời giải" trên chưa hoàn thiện :3

Lâu lắm rồi em không đăng gì :3 

Lời giải của em kiểu biến hình.

Để đến được kết luận thì em sử dụng các kết quả sau.

Định nghĩa cực trực giao. Cho trước tam giác $ABC$ và đường thẳng $\ell$. Lấy $D$, $E$, $F$ là hình chiếu vuông góc của $\ell$ lên $BC$, $CA$, $AB$.

Khi đó các đường thẳng qua  $D$, $E$, $F$ và lần lượt vuông góc với  $BC$, $CA$, $AB$ đồng quy tại một điểm được gọi là cực trực giao của $\ell$ với tam giác $ABC$.

Nhận xét. Từ định nghĩa cực trực giao, ta có được một chú ý như sau: nếu $\ell$ bị tịnh tiến thành $\ell'$ theo một vector $\overrightarrow{v}$ vuông góc với $\ell $ thì $\overrightarrow{TT'}=\overrightarrow{v}$. Trong đó $T$, $T'$ là cực trực giao của $\ell$, $\ell'$.

Định lý 1. $MN$ là một dây của đường tròn ngoại tiếp tam giác $ABC$ thì cực trực giao của $MN$ với tam giác $ABC$ chính là giao điểm của đường thẳng Simson của $M$ và $N$ với tam giác $ABC$.

Định lý 2. $\ell$ là một đường kính của đường tròn ngoại tiếp tam giác $ABC$. $A'$, $B'$, $C'$ là trung điểm $BC$, $CA$, $AB$ thì cực trực giao của $\ell$ với tam giác $ABC$ là điểm Anti-Steiner của $\ell$ với tam giác $A'B'C'$(bởi vì tâm ngoại tiếp $O$ của tam giác $ABC$ chính là trực tâm của tam giác $A'B'C'$)

----------------------------------

Định lý 2 là một bước trong chứng minh định lý Fontene thứ nhất. Trong file đính kèm(epsilon số 7), bài viết "Đường thẳng Simson" thì định lý 1 được đánh số 11(thực ra định lý 11 là một phát biểu tương đương). Còn định lý 2 có thể tham khảo bài viết(trong file đính kèm).

_______________________________________________________________

Quay trở lại bài toán ban đầu. Ta tịnh tiến $MN$ thành đường kính $\ell_1$, tịnh tiến $PQ$ thành đường kính $\ell_2$.

Gọi $S_1$, $S_2$ là hình chiếu vuông góc của $O$ lên $PQ$, $MN$.

Gọi $K'$, $L'$ là cực trực giao của $\ell_1$, $\ell_2$ với tam giác $ABC$.

Theo nhận xét từ đầu post:

\[\overrightarrow{KK'}=\overrightarrow{S_2O}\qquad \overrightarrow{LL'}=\overrightarrow{S_1O}\]

Gọi $T$, $T'$ là trung điểm $KL$ và $K'L'$.

Theo định lý 2, $K'$, $L'$ là điểm Anti-Steiner của $\ell_1$, $\ell_2$ với tam giác $A'B'C'$, mà chúng lại vuông góc nên $K'L'$ là đường kính của đường tròn chín điểm. Nghĩa là $T'$ chính là tâm đường tròn chín điểm, tức là trung điểm của $OH$.

\[2\overrightarrow{TT'}=\overrightarrow{KK'}+\overrightarrow{LL'}=\overrightarrow{S_2O}+\overrightarrow{S_1O}=\overrightarrow{SO}\]

Điều này chứng tỏ rằng $T$ là trung điểm $HS$.

_______________________________________________________________

Cuối cùng, em muốn nhờ thầy đề nghị bài toán mới.

Lâu lắm rồi em không có đóng góp gì cho chuyên mục.

Bài toán tuần này của thầy khá lạ. Phía trên các bạn đều cho những lời giải với góc, đường tròn. Em thì vẫn chưa giải được, tuy nhiên em đã nảy ra ý định đưa nó về một bài toán mang tính xạ ảnh. Em có nhận xét là nếu $(PAD)$ và $(PBC)$ có điểm chung $P$ và $Q$, $PQ$ cắt $CD$ tại $I$ thì $\overline{IM}\cdot\overline{ID}=\overline{IN}\cdot\overline{IC}$. Như vậy, em có một tổng quát như sau:

$ABCD$ là hình thang với hai đáy $AB\parallel CD$. $AD$ cắt $BC$ tại $P$, $AC$ cắt $BD$ tại $K$.

$O$, $M$, $N$ thuộc $CD$ sao cho $\dfrac{\overline{OM}}{\overline{OC}}=\dfrac{\overline{ON}}{\overline{OD}}$. $H$ là điểm bất kì trên $PO$, $BH$ và $AH$ lần lượt cắt $AM$, $BN$ tại $E$, $F$. $DF$ cắt $CE$ tại $Q$.

Chứng minh rằng $P$, $K$, $Q$ thẳng hàng.

Em có một số suy nghĩ như này.

Hoàn toàn có thể dùng góc định hướng cho lời giải chặt chẽ.

Đây lại là một bài toán đường tròn tiếp xúc mà không lộ tiếp điểm, và kiểu bài toán này có lẽ cũng không còn hiếm, khi mà trong chứng minh, tiếp điểm thường là điểm Miquel của một tứ giác toàn phần nào đó. Các bước giải quyết của kiểu bài này có lẽ chỉ cần chứng minh được hai đường tròn cần chứng minh tiếp xúc đi qua điểm Miquel và rồi cộng góc để chứng minh chúng tiếp xúc.

Như bài toán trên đây, các tứ giác toàn phần $(BC,CA,AB,EF)$ và $(BC,CA,AB,MN)$ có chung điểm Miquel $T$ (Cách kí hiệu tứ giác toàn phần này không quen thuộc nhưng chính tắc và không phụ thuộc hình vẽ, không cần tới thứ tự đỉnh). Có được điểm Miquel chung đó là nhờ $\dfrac{\overline{BN}}{\overline{BF}}=\dfrac{\overline{CM}}{\overline{CE}}$.

Nếu như đặt ra vấn đề sau:

Vấn đề 1. Cho trước $\triangle ABC$. $E$, $M$ thuộc $AC$, $F$, $N$ thuộc $AB$ sao cho  $\dfrac{\overline{BN}}{\overline{BF}}=\dfrac{\overline{CM}}{\overline{CE}}$. Lúc này thì ta hoàn toàn chắc chắn $(ABC)$ và tam giác tạo bởi các đường thẳng $BC$, $MN$, $EF$ có điểm chung là điểm Miquel của tứ giác toàn phần $(BC,CA,AB,EF)$ - có điểm chung là một điều kiện cần để có sự tiếp xúc.

Tìm điều kiện của $E$, $F$, $M$, $N$ để $(ABC)$ và đường tròn ngoại tiếp của tam giác tạo bởi các đường thẳng $BC$, $MN$, $EF$ tiếp xúc nhau.

Cách giải quyết chính là phát biểu của bài toán của thầy, thậm chí đó còn là phát biểu tốt vì hoàn toàn dựng bằng hình học. Nhưng chưa dừng lại ở đó, em nghĩ tới vấn đề tổng quát hơn nữa như sau

Vấn đề 2. Cho trước $\triangle ABC$. $E$, $M$, $X$ thuộc $AC$, $F$, $N$, $Y$ thuộc $AB$ sao cho  $\dfrac{\overline{BN}}{\overline{BF}}=\dfrac{\overline{CM}}{\overline{CE}}$, $\dfrac{\overline{BN}}{\overline{BY}}=\dfrac{\overline{CM}}{\overline{CX}}$. Như vậy là ta cũng có $(ABC)$ và đường tròn ngoại tiếp của tam giác tạo bởi ba đường thẳng $MN$, $EF$, $XY$ có điểm chung là điểm Miquel của tứ giác toàn phần $(BC,CA,AB,EF)$.

Tìm điều kiện của $E$, $F$, $M$, $N$, $X$, $Y$ sao cho  $(ABC)$ và đường tròn ngoại tiếp của tam giác tạo bởi ba đường thẳng $MN$, $EF$, $XY$ tiếp xúc nhau.

Sẽ thật tuyệt nếu có một điều kiện mà có thể phát biểu một cách đơn giản, sơ cấp, sẽ càng hay hơn nếu chỉ dựng bằng các tính chất hình học(em dựng bằng parabola   ). Vấn đề 2 là kiểu bài tổng quát nhất có thể cho dạng bài hai đường tròn tiếp xúc nhau tại điểm Miquel.

Em cho rằng nếu giải quyết vấn đề 2 thì có thể khép lại kiểu bài này MỘT LẦN VÀ MÃI MÃI và có thể chế biến được nhiều thứ.

Em rất mong thầy và các bạn quan tâm tìm hiểu.

Em làm như sau.

Lấy $A'B'C'$ là tam giác tạo bởi tiếp tuyến tại $A$, $B$, $C$ của $(O)$.

Ý tưởng của em là chỉ ra $P$ là trực tâm $\triangle A'B'C'$.

Gọi $P'$ là trực tâm $\triangle A'B'C'$.

$X$, $Y$ lần lượt là hình chiếu vuông góc của $B'$, $C'$ lên $BC$.

$T$ là điểm đối xứng với $O$ qua $BC$. $AD'$ là đường cao của $\triangle ABC$.

Có đoạn này thì do muốn chứng minh không phụ thuộc hình vẽ(độ dài đại số, vector) cho nên em dùng barycentric một chút.

Kí hiệu $a$, $b$, $c$ là độ dài của $BC$, $CA$, $AB$.

$AA'$, $BB'$, $CC'$ đồng quy tại điểm Lemoine $S$, hơn nữa ta có $a^2\overrightarrow{SA}+b^2\overrightarrow{SB}+c^2\overrightarrow{SC}=\overrightarrow{0}$. $\triangle A'B'C'$ là tam giác anticevian của $S$ nên

\[-a^2\overrightarrow{A'A}+b^2\overrightarrow{A'B}+c^2\overrightarrow{A'C}=\overrightarrow{0}\]

\[a^2\overrightarrow{B'A}-b^2\overrightarrow{B'B}+c^2\overrightarrow{B'C}=\overrightarrow{0}\]

\[a^2\overrightarrow{C'A}+b^2\overrightarrow{C'B}-c^2\overrightarrow{C'C}=\overrightarrow{0}\]

Từ đó mà ta thu được rằng $(a^2+c^2-b^2)\overrightarrow{AB'}+(a^2+b^2-c^2)\overrightarrow{AC'}=\overrightarrow{0}$

Trực tâm $H$ của $\triangle ABC$ thỏa mãn $\sum\dfrac{\overrightarrow{HA}}{b^2+c^2-a^2}$ $\Rightarrow$ $(a^2+b^2-c^2)\overrightarrow{D'B}+(a^2-b^2+c^2)\overrightarrow{D'C}=\overrightarrow{0}$

\[\Rightarrow \dfrac{\overline{D'B}}{\overline{D'C}}=\dfrac{\overline{AC'}}{\overline{AB'}}=\dfrac{\overline{D'Y}}{\overline{D'X}}\]

$\Rightarrow \overline{D'B}\cdot\overline{D'X}=\overline{D'C}\cdot\overline{D'Y}$.

$\Rightarrow$ $D'$ thuộc trục đẳng phương của 2 đường tròn đường kính $BB'$ và $CC'$.

Dễ thấy $T$ là trực tâm $\triangle A'BC$.

Định lý. Một đường thẳng $\ell$ cắt $BC$, $CA$, $AB$ tại $D$, $E$, $F$ thì trực tâm $\triangle ABC$, $\triangle AEF$, $\triangle BFD$, $\triangle CDE$ thuộc trục đẳng phương của các đường tròn đường kính $AD$, $BE$, $CF$.

Áp dụng điều này, ta suy ra $P'$, $T$, $D'$ thẳng hàng. Hoàn toàn tương tự, $EK$, $FL$ đi qua trực tâm $\triangle A'B'C'$ - nghĩa là $P$ trùng $P'$.

Và từ đó còn dẫn tới $A'$, $P$, $Q$ thẳng hàng.

$AO$ song song $QA'$, $AQ$ song song $OA'$ nên $AOA'Q$ là hình bình hành $\Rightarrow \overrightarrow{QA'}=\overrightarrow{AO}=\overrightarrow{OD}$

$\Rightarrow$ $ODA'Q$ là hình bình hành $\Rightarrow$ $DA'$ song song $OQ$. Mà $DR$ song song $OQ$ nên $DR$ đi qua $A'$.

Vậy $DR$ luôn đi qua điểm cố định $A'$.

$\boxed{\text{Lời giải bài toán 82}}$. Bài này khá đơn giản!

Gọi $X,Y,Z$ lần lượt là giao điểm của $(AOX)(BOY)(COZ)$ với $(O)$. Do tứ giác $AOXD$ nội tiếp nên $\angle ADX=180^\circ-\angle AOX=2\angle OAX=2\angle ODX$. Từ đó $DA,DX$ đẳng giác trong $\angle BDC$. Chú ý tam giác $BDC$ đều nên từ đó $AD,AX$ đẳng giác trong $\angle A$. Theo định lí $Napoleon$ thì $AX,BY,CZ$ đồng quy tại điểm đẳng giác với điểm $Napoleon$ của tam giác $ABC$. Gọi điểm đó là $K$.

 

Gọi $OK$ cắt $(AOX)$ tại $T$ thì $OA^2=OK.OT$ từ đó $T$ xác định duy nhất trên $OK$. Mặt khác do $OA=OB=OC$ nên ba đường tròn $(AOX)(BOY)(COZ)$ đồng quy tại $T.\blacksquare$

 

PS. Kết quả về ba đường tròn đồng quy dạng này thì khá nhiều và quen thuộc với các chứng minh hoàn toàn tương tự như trên. 

Một kết quả khác như sau. Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Gọi $X,Y,Z$ lần lượt là đối xứng của $A,B,C$ qua $BC,CA,AB$. Khi đó $(AOX)(BOY)(COZ)$ đồng quy.

Chứng minh hoàn toán tương tự như trên, chú ý điểm cần tìm ở đây là điểm $Konista$ của tam giác $ABC$.

Bảo chỉ chưa đúng tên gọi thôi.

Điểm Napoleon thì khác(không có trong bài này): dựng ra ngoài các tam giác $A'BC$, $B'CA$, $C'AB$ cân tại  $A'$, $B'$, $C'$ và có góc ở đáy bằng 30 độ thì $AA'$, $BB'$, $CC'$ đồng quy tại điểm Napoleon.

$AD$, $BE$, $CF$ đồng quy tại điểm Fermat thứ nhất ($X_{13}$). $AX$, $AD$ đẳng giác, $AX$ đi qua đẳng giác của điểm Fermat. Đẳng giác của điểm Fermat thứ nhất là điểm isodynamic thứ nhất (một trong hai giao điểm của 3 đường tròn Apollonius) và điểm này là $X_{15}$, tên tại ETC(Encyclopedia of Triangle Centers).

Như vậy là điểm $K$ và điểm $T$ như Bảo đề cập trong chứng minh chính lần lượt là hai điểm isodynamic thứ nhất và thứ hai $(X_{15},X_{16})$.

Trường hợp lấy đối xứng qua ba cạnh tam giác thì ta được định lý Musselman, giao điểm của ba đường tròn là tâm ngoại tiếp và nghịch đảo của điểm Kosnita $(X_{54})$ qua đường tròn ngoại tiếp - điểm này là $X_{1157}$.

Một trong các cách tổng quát: $P$ là điểm thỏa mãn $PQ$ song song với đường thẳng Euler ($Q$ là đẳng giác của $P$). $PA$, $PB$, $PC$ cắt $(PBC)$, $(PCA)$, $(PAB)$ tại $D$, $E$, $F$ thì $(OAD)$, $(OBE)$, $(OCF)$ đồng trục.

Mình đề nghị bài mới.

Bài sau được đặc biệt hóa từ kết quả mình chế (bài tổng quát thì không sơ cấp tí nào).

$\boxed{\text{Bài toán 82}}$ $O$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Dựng ra ngoài tam giác $ABC$ các tam giác đều $DBC$, $ECA$, $FAB$.

Chứng minh rằng các đường tròn $(OAD)$, $(OBE)$, $(OCF)$ còn một điểm chung khác $O$.

Bài 81 này có phát biểu trông rất lạ.

Lời giải bài 81(hơi phức tạp, hi vọng có lời giải đơn giản hơn)

Gọi $I_a$, $I_b$, $I_c$ là tâm bàng tiếp góc $A,B,C$ của $\triangle ABC$.

Ta có $\overline{II_a}\cdot\overline{IA}=\overline{II_b}\cdot\overline{IB}=\overline{II_c}\cdot\overline{IC}=k$.

Xét phép nghịch đảo cực $I$, phương tích $k$ là $I^k_I$.

\[I^k_I: D,E\mapsto\text{đối xứng của $I_b$, $I_c$ qua $B$, $C$}\]

Có điều này do $I^k_I$ biến $AC$ thành $(II_cI_a)$  nên nó biến $D$ thành giao điểm khác $I$ của $IB$ với $(II_aI_c)$ - chính là đối xứng của $I_b$ qua $B$.

Gọi điểm đối xứng với $I_b$, $I_c$ qua $B$, $C$ là $B'$, $C'$. Như vậy cần phải chứng minh $IA$ đi qua điểm Kosnita của $\triangle IB'C'$ (điểm Kosnita là điểm đẳng giác của tâm đường tròn 9 điểm). Gọi $X$ là tiếp điểm của $(I)$ với $BC$, ta đã quen thuộc với tính chất $IA$ đi qua tâm ngoại tiếp $\triangle IBC$ nên $IA$, $IX$ đẳng giác với góc $(IB',IC')$.

Do vậy ta sẽ chứng minh $IX$ đi qua tâm đường tròn chín điểm của $\triangle IB'C'$.

Cấu hình có vẻ vẫn chưa đủ liên kết để giải quyết.

Ý tưởng của mình xuất phát từ việc để ý tới chỗ này: $B$, $C$ là trung điểm $I_bB'$, $I_cC'$. $I_bB'$, $I_cC'$ cắt nhau tại $I$, ta sẽ có tâm của $(IBC)$ là trung điểm của đoạn nối tâm $(IB'C')$ và $(II_bI_c)$(chúng đồng trục, rút ra từ tỉ số phương tích) và hệ quả là trực tâm $\triangle IBC$ là trung điểm của đoạn nối trực tâm $\triangle IB'C'$ và $\triangle II_bI_c$.

Kí hiệu $H_1$, $O_1$, $N_1$ là trực tâm, tâm ngoại tiếp, tâm đường tròn chín điểm của $\triangle IB'C'$.

$H_2$, $O_2$, $N_2$  là trực tâm, tâm ngoại tiếp, tâm đường tròn chín điểm của $\triangle IBC$.

$H_3$, $O_3$, $N_3$  là trực tâm, tâm ngoại tiếp, tâm đường tròn chín điểm của $\triangle II_bI_c$

Cần chỉ ra $N_1$ thuộc $IX$, hay $IH_2$ là xong.

$H_3$ chính là $I_a$ và $N_3$ chính là $O$. Theo định lý ERIQ thì $N_1$ là đối xứng của $O$ qua $N_2$.

Đến đây mọi thứ đã quá rõ ràng: $\triangle IBC$, $O$ thuộc trung trực $BC$. $N_2$ là tâm đường tròn chín điểm của $\triangle IBC$. Đối xứng của $O$ qua $N_2$ thuộc đường cao ứng với $I$ của $\triangle IBC$.

Điều này là rõ ràng bởi đường cao ứng với $I$ và trung trực của $BC$ đối xứng nhau qua tâm đường tròn chín điểm của $\triangle IBC$.

Hic, bài 78 này rối quá ạ.

Em đóng góp ĐÚNG 1 BƯỚC để làm đơn giản đi một tí, đó là chỉ ra $R$, $I_a$, $H$ thẳng hàng, nói cách khác là $RI_a$ vuông góc $OI$.

Nhưng nếu lấy $A'$, $B'$, $C'$ lần lượt là chân các phân giác ngoài góc $A$, $B$, $C$ thì $OI\perp \overline{A'B'C'}$. Do vậy có thể đưa về chứng minh $RI_a$ song song $\overline{A'B'C'}$, mà hướng đi này có vẻ khả thi hơn hướng chứng minh vuông góc.

Ý nhỏ này có thể tổng quát: $\triangle ABC$ và một điểm $P$ bất kì $PA$, $PB$, $PC$ cắt $BC$, $CA$, $AB$ tại $D$, $E$, $F$. $EF$, $FD$, $DE$ cắt $BC$, $CA$, $AB$ tại $A'$, $B'$, $C'$. $Y$, $Z$ thuộc $CA$, $AB$ sao cho $BY$, $CZ$ lần lượt song song $DE$, $DF$. $YZ$ cắt $BC$ tại $R$ thì $AR$ song song $\overline{A'B'C'}$.

Để chứng minh $AR$ song song $\overline{A'B'C'}$ thì ta cần có được $(AA',AR,AB,AC)=\dfrac{\overline{A'C'}}{\overline{A'B'}}$.

Đến đây thì chỉ cần áp dụng các định lý Thales, Menelaus @@

Để cho tiện trong việc biểu diễn các tỉ số, có thể giả sử $x\overrightarrow{PA}+y\overrightarrow{PB}+z\overrightarrow{PC}=\overrightarrow{0}$.

Như vậy thì $\dfrac{\overline{DB}}{\overline{DC}}=-\dfrac{z}{y}$, $\dfrac{\overline{EC}}{\overline{EA}}=-\dfrac{x}{z}$, $\dfrac{\overline{FA}}{\overline{FB}}=-\dfrac{y}{x}$.

\[(AA',AR,AB,AC)=(A',R,B,C)=\dfrac{\overline{A'B}}{\overline{A'C}}\cdot\dfrac{\overline{RC}}{\overline{RB}}=\dfrac{z}{y}\cdot\dfrac{\overline{RC}}{\overline{RB}}\]

Theo Menelaus

\[\dfrac{\overline{RC}}{\overline{RB}}=\dfrac{\overline{YC}}{\overline{YA}}\cdot\dfrac{\overline{ZA}}{\overline{ZB}}\]

\[\dfrac{\overline{CY}}{\overline{CA}}=\dfrac{\overline{CY}}{\overline{CE}}\cdot\dfrac{\overline{CE}}{\overline{CA}}=\dfrac{\overline{CB}}{\overline{CD}}\cdot\dfrac{\overline{CE}}{\overline{CA}}=\dfrac{y+z}{y}\cdot\dfrac{x}{z+x}\]

\[\Rightarrow \dfrac{\overline{YA}}{\overline{YC}}=\dfrac{z(x-y)}{x(y+z)}\]

Tương tự $\dfrac{\overline{ZA}}{\overline{ZB}}=\dfrac{y(x-z)}{x(y+z)}$

\[\Longrightarrow \dfrac{\overline{RC}}{\overline{RB}}=\dfrac{y(x-z)}{z(x-y)}\Longrightarrow (A',R,B,C)=\dfrac{x-z}{x-y}\]

\[\dfrac{\overline{A'C'}}{\overline{A'B'}}=\dfrac{\overline{BC'}}{\overline{BA}}\cdot\dfrac{\overline{CA}}{\overline{CB'}}=\dfrac{x}{x-y}\cdot\dfrac{x-z}{x}=\dfrac{x-z}{x-y}=(A',R,B,C)\]

Kết thúc

__________________________________

Quay lại bài toán cũ, vậy là đã chỉ ra được $R$, $I_a$, $H$ thẳng hàng, nên $H$ có thể xác định đơn giản là hình chiếu vuông góc của $I_a$ lên $OI$.

 

vietnam in my heart đã viết

"Bài toán 

7777 do Bảo đề nghị có lẽ được tạo ra nhờ bài toán sau: Cho tam giác XYZXYZ ngoại tiếp (O)(O). Các tiếp điểm của (O)(O) trên YZ,ZX,XY là A,B,C. Một đường tròn tâm O bất kỳ cắt tia đối của các tia OA,OB,OC(hoặc cắt các tia OA,OB,OC) lần lượt tại L,M,N. Khi đó XL,YM,ZN đồng quy 

Bài này có lẽ đã cũ nhưng em(mình) chưa tìm được một lời giải nào hay, tính toán ít nên nhờ thầy và mọi người giúp đỡ  :)"

 

Thực ra $\triangle XYZ$ và $\triangle LMN$ trực giao(orthologic) và có 2 tâm trực giao(orthology center) trùng nhau (chính là $O$), nên theo định lý Sondat, hai tam giác trực giao có tâm trực giao trùng nhau thì thấu xạ. Chứng minh cho trường hợp này có thể xem cho bài tổng quát hơn tại post #2 http://artofproblems...1181784p5767010

Ok Khánh, bài tổng quát thì thầy Hùng đã post tại http://artofproblems...1136264p5307949

Và hoàn toàn có thể tổng quát tiếp nhưng không còn đơn giản và phổ thông nữa @@

_________________________________

Trường hợp $P=I$ đơn giản và đặc biệt hơn cả, cách chứng minh của mình thì dùng barycentric nhưng mà một cách ngắn gọn.

Chú ý. $\dfrac{\overline{DB}}{\overline{DC}}=\dfrac{\alpha-\beta}{\alpha-\gamma}$, $\dfrac{\overline{EC}}{\overline{EA}}=\dfrac{\beta-\gamma}{\beta-\alpha}$, $\dfrac{\overline{FA}}{\overline{FB}}=\dfrac{\gamma-\alpha}{\gamma-\beta}$ - có được các tỉ số có "dạng" như thế khi và chỉ khi $AD$, $BE$, $CF$ song song.

Lưu ý $\triangle I_aI_bI_c$ và $\triangle I_aBC$ đồng dạng nghịch. Theo đó, lấy $X$ trên $I_bI_c$ sao cho $\dfrac{\overline{XI_b}}{\overline{XI_c}}=\dfrac{\overline{DB}}{\overline{DC}}$ thì $I_aX$, $I_aD$ đẳng giác với $\widehat{I_cI_aI_b}$. Tương tự, lấy $Y$, $Z$ thì ta có $I_bY$, $I_bE$ đẳng giác với $\widehat{I_aI_bI_c}$; $I_cZ$, $I_cF$ đẳng giác với $\widehat{I_aI_cI_b}$. Áp dụng chú ý trên cho $\triangle I_aI_bI_c$ thì ta được $I_aX$, $I_bY$, $I_cZ$ đôi một song song. Điều đó dẫn tới $I_aD$, $I_bE$, $I_cF$ đồng quy trên $(I_aI_bI_c)$.

Lời giải cho bài 74

Ý tưởng chủ đạo của em là tính chất sau: $P$, $Q$ đẳng giác khi với $\triangle ABC$ khi và chỉ khi chúng thỏa mãn ít nhất 2 trong 3 đẳng thức

\[(PB,PC)+(QB,QC)=(AB,AC);\quad (PC,PA)+(QC,QA)=(BC,BA);\quad (PA,PB)+(QA,QB)=(CA,CB)\]

Điều này được chứng minh bằng điểm trùng.

Quay trở lại bài toán, do tính đối xứng, chỉ cần cm $(SB,SC)+(TB,TC)=(DB,DC)+(XB,XC)=(AB,AC)$ là đủ.

\[(DB,DC)=(BD,BQ)+(QB,QC)+(CQ,CD)=(BQ,BP)+(QB,QC)+(CP,CQ)=2(QB,QC)-(PB,PC)\]

\[(XB,XC)=(BX,BL)+(LB,LC)+(CL,CB)=(BL,BK)+(LB,LC)+(CK,CL)=2(LB,LC)-(KB,KC)\]

Suy ra

\[(DB,DC)+(XB,XC)=2(QB,QC)+2(LB,LC)-(KB,KC)-(PB,PC)=2(AB,AC)-(AB,AC)=(AB,AC)\]

Vậy kết luận $S$, $T$ đẳng giác với $\triangle ABC$.

_____________________________

Mình đề nghị bài tiếp theo

$\boxed{\text{Bài toán 75}}$(đặc biệt hóa)$\triangle ABC$ có $I_a$, $I_b$, $I_c$ là các tâm đường tròn bàng tiếp góc $A$, $B$, $C$.

$D$, $E$, $F$ thuộc $BC$, $CA$, $AB$ sao cho $AD$, $BE$, $CF$ đôi một cùng phương.

Chứng minh $DI_a$, $EI_b$, $FI_c$ đồng quy trên đường tròn ngoại tiếp $\triangle I_aI_bI_c$.

Lời giải bài 71

Đây là file em gửi tới THTT, lời giải của em dùng hình học định hướng.

Lời giải bài 72.

Trong link gốc, bài toán của Telv có tới 4 đường đồng quy. Cái thứ 4 khó hơn.

Theo định lý Steinbart, $AX$, $BY$, $CZ$ đồng quy.

Theo chứng minh của bài 69 thì $XX^*$, $YY^*$, $ZZ^*$ đồng quy.

Với những bài có đúng 1 conic thì ta chỉ cần chứng minh cho đường tròn là đủ.

Nhờ thầy Hùng giúp em đề nghị bài mới.

Lời giải bài 69

Không mắc mớ gì tới vuông góc 

Gọi $D$, $E$, $F$ là giao điểm các cặp $(BZ, CY)$, $(AX,CZ)$, $(AY,BX)$.

Và hóa ra chỉ cần chứng minh $AD$, $BE$, $CF$ đồng quy thôi!

Gọi $T$ là giao điểm của $BE$, $CF$.

Ở đây mình dùng tỉ số kép. $PA$ cắt $BC$ tại $A'$

$(BT,BA,BD,BC)=(BE,BA,BD,BC)=(BE,BA,BZ,BC)=(CE,CA,CZ,CB)=(CX, CA,CP,CA')=(X,A,P,A')$

Giống hệt, ta được $(CT,CA,CD,CB)=(CF,CA,CD,CB)=(X,A,P,A')$

Do đó $BE\cap CF$, $A$, $D$ thẳng hàng, tức là $AD$, $BE$, $CF$ đồng quy.

Quay lại bài của Bảo, $BE$, $CF$ là đường cao nên $AD$ là đường cao.

Mình đề nghị bài tiếp theo

$\boxed{\text{Bài toán 70}}$(Morley point of quadrilateral) Cho 4 đường thẳng $a$, $b$, $c$, $d$ đôi một cắt nhau và không có bộ ba nào đồng quy.

Kí hiệu $\triangle abc$ là tam giác tạo bởi 3 đường thẳng $a$, $b$, $c$.

Gọi $N_a$, $N_b$, $N_c$, $N_d$ là tâm đường tròn 9 điểm của $\triangle bcd$, $\triangle cda$, $\triangle dab$, $\triangle abc$.

Chứng minh các đường thẳng lần lượt qua $N_a$, $N_b$, $N_c$, $N_d$ và vuông góc $a$, $b$, $c$, $d$ đồng quy tại một điểm trên đường thẳng Steiner của tứ giác toàn phần $abcd$.

P.S: Đường thẳng Steiner đã quen thuộc nhưng mình nhắc lại, đó là đường thẳng chứa trực tâm của 4 tam giác $\triangle bcd$, $\triangle cda$, $\triangle dab$, $\triangle abc$.

Hơn nữa, bài này mình đã có lời giải rồi, không tọa độ gì hết, thuần túy hình học thôi.

Em cũng không biết là bài 54 có cách chứng minh như vậy.

Tổng quát hơn là tính chất 6 đường thẳng đồng quy trên đường thẳng Euler mà em đã post tại http://artofproblems...1202141p5914760

Trong post đó em có ghi nguồn.

Tam giác vuông cân là trường hợp của bài 54.

Đặc biệt khi cho tam giác đều thì các đường thẳng sẽ song song với đường thẳng Euler; khi tam giác cân có góc ở đáy là $\dfrac{\pi}{6}$ thì điểm đồng quy là tâm đường tròn chín điểm.