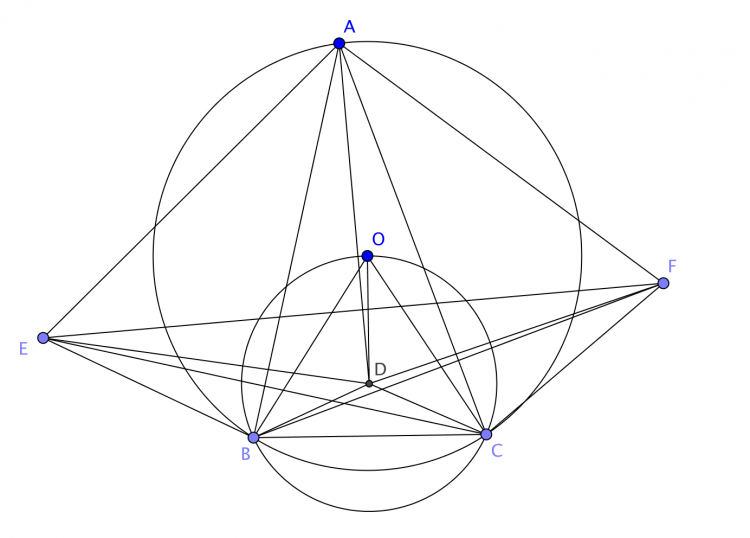
Bài toán 145 (AoPS). Cho tam giác $ABC$ với $\angle BAC<45^{\circ}$. $D$ ở trong tam giác $ABC$ sao cho $BD=CD$ và $\angle BDC=4\angle BAC$. $E$ là đối xứng của $C$ qua $AB$. $F$ là đối xứng của $B$ qua $AC$. Chứng minh rằng $AD\perp EF$.

Lời giải của em như sau:

Lời giải bài toán 145: Gọi $O$ là tâm ngoại tiếp tam giác $ABC$ thì $D$ là tâm ngoại tiếp tam giác $OBC$. Đặt $BC=a,CA=b,AB=c$ và bán kính của $(ABC)$, $(OBC)$ lần lượt là $R,r$, ta sẽ chứng minh rằng $DE^2-DF^2=AE^2-AF^2=b^2-c^2$. Thật vậy, dễ dàng tính được $\angle DBE=\angle A+90^{\circ}+\angle B-\angle C$ và $\angle DBE=\angle A+90^{\circ}+\angle C-\angle B$.

Lại có các đẳng thức $DE^2=a^2+r^2-2ar\cdot cos\angle DBE, \\DF^2=a^2+r^2-2ar\cdot cos\angle DCF$ và $r=\frac{a}{2sin\angle 2A}=\frac{a}{4sin\angle A\cdot cos\angle A}$ nên ta có:

$DE^2-DF^2=2ar(cos\angle DCF-cos\angle DBE)\\= \frac{-a^2\cdot sin(\angle A+90^{\circ})\cdot sin(\angle C-\angle B)}{sin\angle A\cdot cos\angle A}\\=4R^2\cdot sin\angle A\cdot sin(\angle C-\angle B)$

Mặt khác $b^2-c^2=2R^2(cos\angle 2C-cos\angle 2B)=4R^2sin(\angle C+\angle B)sin(\angle C-\angle B)$, dẫn đến $DE^2-DF^2=b^2-c^2=AE^2-AF^2$ hay $AD\perp EF$ $\blacksquare$

 

$\boxed { Bài \ toán \ 110} $ (sách) Cho $\triangle ABC$ nội tiếp $(O)$ , $K,L$ là tâm bàng tiếp góc $\angle B, \angle C$. $(K)$ tiếp xúc $BA,BC$ tại $B_1,B_2$, tương tự ta có $C_1,C_2$. $B_1B_2$ cắt $C_1C_2$ tại $N$. Chứng minh rằng $AN \perp BC$

 

Lời giải của em như sau. Em tính hết ra.

Không mất tính tổng quát, giả sử vị trí các điểm như hình vẽ. Đặt $BC=a, CA=b, AB=c$. Gọi đường cao $AH$ của tam giác $ABC$ cắt $CL,BK,B_1B_2,C_1C_2$ tại $X,Y,T,T'$. Ta có $\angle HT'C_2=\frac{\angle ACB}{2}=\angle ACL$ nên $CXC_1T'$ nội tiếp hay $AX.AT'=AC.AC_1=b(p-b)$. Tương tự thì $AY.AT=AB.AB'=c(p-c)$ nên $\frac{AX}{AY}.\frac{AT'}{AT}=\frac{b(p-b)}{c(p-c)}$. Ta tính được $BH=AB.cos\angle ABC=\frac{c(c^2+a^2-b^2)}{2ca}=\frac{c^2+a^2-b^2}{2a}$, mặt khác theo tính chất đường phân giác thì $\frac{AY}{AB}=\frac{YH}{BH}=\frac{AH}{AB+BH}$ nên $AY=\frac{AB.AH}{AB+BH}=\frac{c.AH}{c+\frac{c^2+a^2-b^2}{2a}}=\frac{2ac.AH}{(c+a-b)(c+a+b)}=\frac{ac.AH}{2p(p-b)}$, tương tự thì $AX=\frac{ab.AH}{2p(p-c)}$. Do đó $\frac{AX}{AY}=\frac{b(p-b)}{c(p-c)}=\frac{AX}{AY}.\frac{AT'}{AT}$, dẫn đến $AT=AT'$ hay $B_1B_2,C_1C_2$ cắt nhau trên $AH$. Vậy $AN\perp BC$ $\blacksquare$

Và em muốn nhờ thầy Hùng đề nghị bài toán mới

Bài toán 108 (Mở rộng ý a) bài toán 7 VMO 2017). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$. Trung trực $BC$ cắt $(K)$ tại $M,N$. $P$ là điểm thuộc $(K)$. $PM$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $L$. Chứng minh rằng $AL,PN$ và $BC$ đồng quy.

 

Figure4244.png

Không rõ lời giải của em có nhầm lẫn gì không, nhưng em thấy lời giải khá ngắn.

Gọi $NP$ cắt $BC$ tại $T$, $EF$ cắt $BC$ tại $S$ thì $PN$ là phân giác $\angle BPC$ nên $(ST,BC)=-1$, từ đó dễ dàng có ngay $AL$ đi qua $T$.

Bài toán tiếp theo là của thầy Hùng, là bài toán 25 trong tập bài giảng của thầy tại đây: http://analgeomatica...t-chuyen-i.html. Nói ngoài lề một ít, đây là tập bài giảng làm em rất ấn tượng, một phần vì các bài sau rất khó, và mỗi lần sau một khoảng thời gian giải lại thì lại tìm thấy những điều thú vị.

Bài toán 109 (Sáng tác từ Serbia 2013 và Iran 2015): Cho tam giác $ABC$ nội tiếp $(O)$, $X$ là điểm trên cung nhỏ $BC$ sao cho nếu $E,F$ là hình chiếu của $X$ trên $IB,IC$ thì trung điểm $EF$ nằm trên trung trực $BC$. Gọi $J$ là tâm bàng tiếp góc $\angle BAC$ của tam giác $ABC$. Chứng minh rằng $XJ$ đi qua trung điểm cung lớn $BC$ của $(O)$.

Bài toán 105.(Mở rộng ý a) VMO 2017 bài toán 3). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$. Một đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$ khác $B,C$. $BE$ cắt $CF$ tại $H$. $AH$ cắt $(O)$ tại $D$ khác $A$. Tiếp tuyến tại $E,F$ của $(K)$ lần lượt cắt $DB,DC$ tại $M,N$. Chứng minh rằng $MN\perp OH$.

Bổ đề: Cho tam giác $ABC$ nội tiếp $(O)$. Đường tròn $(K)$ đi qua $B,C$ cắt $CA,AB$ tại $E,F$. $BE$ cắt $CF$ tại $H$. Gọi $AT$ là đường kính của $(O)$. Khi đó $T,K,H$ thẳng hàng.

Lời giải bài toán 105: Gọi $L$ là giao điểm của $ME,AH$ thì ta có $\angle LEB=\angle ACB=\angle ADB$ nên $BDEL$ nội tiếp, dẫn đến $HL.HD=HE.HB=HF.HC$ hay $CDFL$ nội tiếp. Từ đó $\angle LFC=\angle ADC=\angle ADC$ nên $FL$ là tiếp tuyến của $(K)$ và $N,F,L$ thẳng hàng. Mặt khác $ML.ME=MB.MD$ và $NL.NF=NC.ND$ nên $MN$ chính là trục đẳng phương của $(LEF)$ và $(K)$, nên ta chỉ cần chứng minh tâm của $(LEF)$ nằm trên $OH$ hay $OH$ chia đôi $LK$. Gọi $AT$ là đường kính của $(O)$, do $BCEF$ nội tiếp nên dễ dàng chứng minh được $EF\perp AT$, mà $EF||LK$ (tính chất tiếp tuyến) nên $LK||EF$. Theo bổ đề, $T,K,H$ thẳng hàng mà $OH$ chia đôi $AT$ nên $OH$ chia đôi $LK$. Vậy $MN\perp OH$.

Một hệ quả của bài toán là $MN,EF,BC$ đồng quy, Thật vậy, nếu gọi $EF$ cắt $BC$ tại $S$ thì $SE.SF=SB.SC$ nên $S$ nằm trên trục đẳng phương của $(LEF)$ và $(K)$ hay $MN,EF,BC$ đồng quy.

Hình vẽ bài toán 105 ở phần dưới.

Bài toán 106 (Sưu tầm): Cho tam giác $ABC$ nhọn có $AD,BE,CF$ là đường cao và trực tâm $H$. $I$ là tâm nội tiếp tam giác $AEF$. Gọi $M,N$ là điểm trên $(IAB),(IAC)$ sao cho $BM,CN$ là phân giác $\angle ABC, \angle ACB$. Chứng minh rằng trung tuyển qua $M,N$ của tam giác $MHB,NHC$ cắt nhau trên $(DEF)$.

Được sự đồng ý của thầy Hùng, em đề nghị bài toán tiếp theo, cũng là 1 bài của thầy.

Bài toán 166. Cho tam giác $ABC$ nhọn nội tiếp đường tròn $(O)$ bán kính $R$ có $I$ là tâm nội tiếp, $AD$ là đường cao. $K$ là điểm trên tia $AD$ sao cho $AK=2R$. $M$ là hình chiếu của $B$ trên $IK$. Gọi $AD$ cắt lại $(O)$ tại $N$. Giả sử rằng $IK\parallel AB$. Chứng minh rằng $MN\parallel ID$.

Theo đề nghị của anh Khánh, em đề xuất bài toán tiếp theo, có lẽ là của anh Phạm Hy Hiếu, HCB IMO năm 2009.

Bài toán 168. Cho tam giác $ABC$ nội tiếp $(O)$ có $BC>CA>AB$ và $I$ là tâm nội tiếp. $AI$ cắt lại $(O)$ tại $K$. $M$ là trung điểm $BC$. Gọi $N$ đối xứng với $I$ qua $M$. $KN$ cắt lại $(O)$ tại $L$. Chứng minh rằng $LB=LC+LA$.

Anh Hiếu nhờ em đề xuất tiếp bài toán sau đây:

Bài toán 179: Cho tam giác $ABC$ có đường cao $BE,CF$. $M$ là hình chiếu của $A$ trên $EF$. $N,P$ là trung điểm $BE,CF$. Chứng minh rằng hai tam giác $ABC,MNP$ đồng dạng.

Bài toán 174. Cho $\Delta ABC$ có 1 điểm $D$ bất kì thuộc đường thẳng $BC$ sao cho $D$ và $B$ nằm khác phía so với $C$. Gọi $I$ và $I_1$ l ần lượt là tâm nội tiếp $\Delta ABC$ và $\Delta ACD$. Chứng minh rằng trục đẳng phương của $(I)$ và $(I')$ đi qua 1 điểm cố định khi $D$ thay đổi.

Đây là bài toán IMO Shortlist 2004, có thể xem tại đây: https://artofproblem...c6h41033p257883

Bài toán sau trích từ chuỗi bài giảng của thầy Hùng tại trường Đông miền Nam 2015:

Bài toán 175. Cho tam giác $ABC$ nội tiếp $(O)$ có trực tâm $H$. $AD,AM$ lần lượt là đối trung và trung tuyến. Gọi $P,Q$ đối xứng $H$ qua $AD,AM$ và $R$ đối xứng $H$ qua $D$. Chứng minh rằng $(PQR)$ tiếp xúc $(O)$.

Bài toán 170: Cho $\triangle ABC$. $M\in (BC)$ sao cho $M$ nằm trog $\triangle ABC$. Gọi $D,E,F$ lần lượt là hình chiếu của $M$ trên $BC,CA,AB$. $ME$ cắt $AB$ tại $P$, $MF$ cắt $AC$ tại $Q$, $PQ$ cắt $BC$ tại $K$. $H$ đối xứng với $M$ qua trung điểm của $PQ$. CMR: $HK\perp AD$

Lời giải sau tham khảo từ Nguyễn Lê Phước trên Facebook.

Lời giải: Ta có hai tam giác $PBM$ và $QMC$ đồng dạng g.g do $\angle PBM=90^{\circ}-\angle BMF=\angle QMC$ và $\angle BPM=\angle MQC$, từ đó $\frac{PB}{QM}=\frac{PM}{QC}$. Dễ thấy rằng $MPHQ$ là hình bình hành nên $MQ=HP$ và $MP=HQ$, từ đó $\frac{PB}{PH}=\frac{QH}{QC}$ hay tam giác $PBH$ đồng dạng tam giác $QHC$ (c.g.c). Gọi $R$ là hình chiếu của $H$ trên $BC$ thì $\angle PRQ=\angle PRH+\angle QRH=\angle PBH+\angle QCH=90^{\circ}$, lại theo một bài toán quen thuộc là $ND=NR$ nên các điểm $D,E,F,P,Q,R$ thuộc một đường tròn. Gọi $HK$ cắt $(APQ)$ tại $S$ thì $KD.KR=KP.KQ=KH.KS$ dẫn đến $DSHR$ nội tiếp. Do đó $\angle DSH=90^{\circ}=\angle ASH$ nên $A,S,D$ thẳng hàng. Vậy $AD\perp HK$ $\blacksquare$

Một kết quả thú vị cho bài toán: $M.H$ là hai điểm đẳng giác trong tam giác $ABC$.

Theo đề nghị của anh Phương, em đề xuất tiếp bài toán sau của thầy Hùng.

Bài toán 169. Cho tam giác $ABC$ có $D$ là điểm bất kỳ trên đường cao từ $A$. Đường tròn $(K)$ đường kính $AD$ cắt $CA,AB$ tại $E,F$. Tiếp tuyến tại $E,F$ của $(K)$ cắt $BC$ tại $M,N$. Gọi $EB$ cắt $FC$ tại $P$, $EN$ cắt $FM$ tại $Q$. Chứng minh rằng $PQ$ luôn đi qua điểm cố định khi $D$ thay đổi.

Em giải thích rõ hơn phần tính toán để có được $IN||AF$.

Đặt $BC=a,CA=b,AB=c(b\neq c)$ thì dễ dàng có $\frac{IE}{IA}=\frac{a}{b+c}$. Mặt khác cũng tính được $BE=\frac{ca}{c+b}$ nên $NE=BN-BE=\frac{a}{2}-\frac{ca}{c+b}=\frac{a(b-c)}{2(b+c)}$. Hơn nữa $NF=NC-CF=\frac{a}{2}-\frac{c+a-b}{2}=\frac{b-c}{2}$ nên $\frac{NE}{NF}=\frac{a(b-c)}{2(b+c)}:\frac{b-c}{2}=\frac{a}{b+c}=\frac{IE}{IA}$. Theo định lý Thales đảo, $IN||AF$.

Bài toán 103 (Mathematical Refections 6/2014). Cho tam giác $ABC$ nội tiếp $(\Gamma)$ có $M$ là điểm chính giữa cung $BC$ không chứa $A$. Gọi $l_{b},l_{c}$ là đường thẳng qua $B,C$ song song $AM$ và cắt lại $(\Gamma)$ tại $P,Q$. $PQ$ cắt $AB,AC$ tại $X,Y$. $AM$ cắt lại $(AXY)$ tại $N$. Chứng minh rằng trung trực $BC,XY,MN$ đồng quy.

 

Bài toán 102 (Tập huấn đội IMO 2016). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ cố định. $B$, $C$ cố định, $A$ di chuyển trên $(O)$. $I$ là tâm đường tròn nội tiếp tam giác $ABC$. $K$, $L$ theo thứ tự là trực tâm các tam giác $IAB$, $IAC$. $P$ đối xứng với $O$ qua trung điểm $KL$. Chứng minh rằng $AP$ đi qua một điểm cố định khi $A$ thay đổi.

Lời giải của em như sau.

Trước hết, ta phát biểu hai bổ đề sau:

Bổ đề 1: Hai tam giác đồng dạng có hai cặp cạnh tương ứng vuông góc thì cặp cạnh còn lại cũng vuông góc.

Bổ đề 2: $KL,AF$ vuông góc trên $(I)$ với $F$ là tiếp điểm đường tròn bàng tiếp góc $\angle BAC$ của tam giác $ABC$.

Hai bổ đề trên đều quen thuộc nên không trình bày lại phép chứng minh tại đây, riêng bổ đề 2 chính là hệ quả bài toán 3 trong kỳ thi Olympic Sharygin vòng 1 năm 2017. Quay trở lại bài toán ban đầu. Do trường hợp $AB=AC$ là hiển nhiên nên không mất tính tổng quát, ta xét trường hợp $AB<AC$ và vị trí các điểm như hình vẽ.

Do $K,L$ là trực tâm các tam giác $IAB,IAC$ và $I$ là tâm nội tiếp tam giác $ABC$ nên ta có:

$\angle KAL=\angle KAB+\angle LAC-\angle BAC=90^{o}-\frac{\angle ABC}{2}+90^{o}-\frac{\angle BCA}{2}-\angle BAC=90^{0}-\frac{\angle BAC}{2}$

Gọi $Q$ là điểm sao cho $AQ\perp BC$ và $QP||AL$ thì ta có:

$\angle KAQ=\angle BAK-\angle BAQ=90^{o}-\frac{\angle ABC}{2}-(90^{o}-\angle ABC)=\frac{\angle ABC}{2}=\angle IBC$.

Mặt khác do $\angle AKQ=180^{o}-\angle KAL=180^{o}-(90^{o}-\frac{\angle BAC}{2})=90^{o}+\frac{\angle BAC}{2}=\angle BIC$ nên tam giác $AKQ$ đồng dạng tam giác $BIC$ (g.g). Gọi $M,N$ là trung điểm $AQ,BC$ thì tam giác $AKM$ đồng dạng tam giác $BIN$ (c.g.c). Từ bổ đề dễ dàng có $KM\perp IN$, lại có $KL\perp AF$ nên ta chỉ cần chứng minh rằng $IN||AF$. Nhưng điều này đúng do dễ dàng tính toán theo 3 cạnh tam giác $ABC$ bởi tính chất phân giác để có tỉ lệ $\frac{IE}{IA}=\frac{BC}{CA+AB}=\frac{NE}{NF}$. Từ đó dẫn đến $KM\equiv KL\perp IN$, lại có $\Delta MAL=\Delta MQK$ (g.c.g) nên $ML=MK$ hay $M$ là trung điểm $KL$ hay $M$ cũng là trung điểm $OP$. Lại có $\frac{AQ}{BC}=\frac{AK}{BI}=cot\frac{\angle BAC}{2}$ không đổi nên $AQ$ không đổi. Gọi $R$ là đối xứng của $P$ qua $A$ thì $OR=AQ$ không đổi, lại có $OR||AP\perp BC$ nên $AP$ luôn qua $R$ cố định $\blacksquare$

Thầy có lời giải nào mà để tránh tính toán phần sau không ạ ?

Hình vẽ bài toán:

Em đề nghị bài toán tiếp theo, đã được phát biểu lại cho gọn hơn. Bài toán trích từ đề thi chọn HSG lớp 9 trường THPT chuyên Trần Đại Nghĩa năm ngoái.

Bài toán 99: Cho tam giác $ABC$ có $O$ là tâm ngoại tiếp. Đường thẳng $d$ đi qua $O$ sao cho $B,C$ nằm cùng phía với $d$. Gọi $M,N$ là hình chiếu của $B,C$ trên $d$. Đường thẳng qua $M$ vuông góc $CA$ cắt đường thẳng qua $N$ vuông góc $AB$ tại $T$. Chứng minh rằng $T$ luôn thuộc đường tròn cố định khi $d$ thay đổi.

Theo cái nhìn chủ quan của em thì đây là một bài toán có cấu hình đẹp và thú vị, nên em rất mong thầy Hùng và các anh chị đóng góp những mở rộng của bài toán trên.

Lời giải sau do bạn Nguyễn Lê Phước gửi tới tác giả.

 

Figure4051.png

 

Lời giải bài toán 101. Gọi $NI$ cắt $HK$ tại $S$, $MI$ cắt $HL$ tại $T$ thì $S,T$ là tâm bàng tiếp tam giác $ANH,AMH$. Từ đó $\angle ASE=45^\circ=\angle AHL$ và $\angle AES=90^\circ+\angle ANE=\angle ALH$. Từ đó hai tam giác $ASE$ và $ALH$ đồng dạng g.g. Lại có $\angle ATH=90^\circ-\frac{\angle AMN}{2}=180^\circ-\angle AIN=\angle AIS$. Từ đó hai tam giác $ATH$ và $AIS$ đồng dạng g.g. Vậy $\frac{ES}{EI}=\frac{LH}{LT}$. Tương tự $\frac{FT}{FI}=\frac{KH}{KS}$. Từ đó $\frac{FI}{FT}.\frac{LT}{LH}=\frac{EI}{ES}.\frac{KS}{KH}$. Dùng định lý Menelaus dễ thấy $FL,ES$ cùng đi qua một điểm trên $IH$.

 

Lời giải khác của bạn Nguyễn Đức Bảo có thể xem tại http://artofproblems...1308940p7009306, bài toán này nằm trong chuỗi bài mở rộng bài toán IMO 2009 của tác giả http://analgeomatica...-2009-ngay.html

 

Bài toán 102 (Tập huấn đội IMO 2016). Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và $P$ di chuyển trên cung $BC$ không chứa $A$. Đối xứng của $PA$ qua $PB$, $PC$ lần lượt cắt $AB$, $AC$ tại $F$, $E$. Một đường thẳng vuông góc với $PA$ tại một điểm chia $PA$ theo tỉ số cố định cắt tiếp tuyến tại $A$ của $(AEF)$ tại $Q$. Chứng minh rằng $Q$ luôn thuộc đường thẳng cố định khi $P$ thay đổi.

Trong quá trình cố gắng chứng minh bài toán, em phát hiện ra một số tính chất khác như sau. Không mất tính tổng quát, ta giả sử rằng $AB<AC$.

Tính chất 1: $EF$ đi qua $D$ là chân đường phân giác ngoài từ $A$ của $\Delta ABC$.

Thật vậy, do $NE$ là phân giác $\angle ANC$ nên $\frac{EC}{EA}=\frac{NC}{NA}=\frac{AC}{AH}$. Tương tự ta có $\frac{FA}{FB}=\frac{AH}{AB}$ nên nếu gọi $AD$ là phân giác ngoài của $\Delta ABC$ thì theo định lý Menelaus, chứng minh được $D,E,F$ thẳng hàng.

Tính chất 2: $NF,ME,AI$ đồng quy.

Từ tính chất 1 và lưu ý rẳng $AI$ là phân giác $\angle BAC$, lại có $AB,AC$ là hai đường đẳng giác trong $\Delta AMN$ nên gọi $AI$ cắt $BC$ tại $P$ thì $(DP,BC)=(DP,NM)=-1$. Mặt khác gọi $AI$ cắt $EF$ tại $S$ thì $A(DP,BC)=A(DS,FE)=(DS,FE)=-1=(DP,NM)$ nên $SP,NF,ME$ đồng quy hay $NF,ME$ cắt nhau trên $AI$.

Bài toán 98. Cho tam giác $ABC$ giả sử có điểm $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$ đồng thời nếu có các đường tròn $(K)$ qua $P,C$ và đường tròn $(L)$ qua $P,B$ sao cho $(K),(L)$ cắt nhau tại $Q$ khác $P$ thì $BQ$ đi qua giao điểm $E$ của $(K)$ và $AC$ còn $CQ$ đi qua giao điểm $F$ của $(L)$ và $AB$. Chứng minh rằng $BE=CF$.

 

Figure4229.png

 

Nguồn gốc: http://www.cut-the-k.../Stoyanov.shtml

Lời giải của em như sau:

Không mất tính tổng quát, giả sử vị trí các điểm như hình vẽ thì ta có $\angle BFP = \angle BQP = \angle PCA = \angle PBA$ nên $\Delta PBF$ cân tại $P$ hay $PB=PF$. Tương tự ta có $PE=PC$ nên $\Delta PBE=\Delta PFC$ (c.g.c), dẫn đến $BE=CF$.

Mình xin được có một vài ý kiến.

Thiết nghĩ việc sử dụng các bài toán Olympic quá khó cho việc ôn luyện vào THPT chuyên không phải là một việc làm hay. Như bài toán của thầy Nguyễn Minh Hà được lấy từ mục "Thách đấu" trên tạp chí TTT2 tuy lời giải sử dụng kiến thức THCS nhưng không thích hợp trong điều kiện đề thi của THCS. Mình cho rằng với kỳ thi vào lớp chuyên, một bài toán hình học có ý nghĩa là khi không quá dễ, phát biểu đẹp nhưng cũng đồng thời kiểm tra được khả năng đoán nhận tính chất và nhận biết vấn đề của học sinh trong thời gian ngắn. Còn về những tính chất khó đoán nhận hơn, đó lại là câu chuyện sau khi vượt qua kỳ thi đó. Và thật ra đa số các bài toán Olympic đều có lời giải chỉ dùng kiến thức THCS.

Bài toán 91. Cho tam giác $ABC$ nhọn nội tiếp $(O)$. Tiếp tuyến tại $B,C$ của $(O)$ cắt nhau ở $K$. Gọi $I$ đối xứng $O$ qua $BC$. $L$ là trung điểm $OK$. Chứng minh rằng $\angle IAB=\angle LAC$.

Bài 51.1. (Tuymaada, Junior). Cho ba số thực không âm $a,b,c$ thỏa mãn $a^2+b^2+c^2 \geqslant 3.$ Chứng minh rằng
\[(a+b+c)^3 \geqslant 9(ab+bc+ca).\]

Giải: Áp dụng bất đẳng thức AM-GM cho 3 số dương, ta có:

$(a+b+c)^3+(a+b+c)^3+27\geq 9(a+b+c)^2$

$\Rightarrow (a+b+c)^3 +\frac{27}{2}\geq \frac{9}{2}(a+b+c)^2=\frac{9}{2}(a^2+b^2+c^2)+9(ab+bc+ca)\geq \frac{27}{2}+9(ab+bc+ca)$

Từ đó ta có điều phải chứng minh. ĐTXR $\Leftrightarrow a=b=c=1$

Bài 48: Ta xét: $S=(a^2+ac+c^2)(b^2+bd+d^2)-(ab+bc+cd)^2=(ad-bc)(ab+ad+cd)=(ad-bc)(1+ad-bc)=(ad-bc+\frac{1}{2})^2-\frac{1}{4}\geq -\frac{1}{4}$

$\Rightarrow P\geq (ab+bc+cd)^2-\frac{1}{4}=\frac{3}{4}$

Đẳng thức xảy ra tương đương với việc ta có hệ: $\left\{\begin{matrix} ad-bc=-\frac{1}{2}\\ ab+bc+cd=1\\ \end{matrix}\right.$

Hệ này có nghiệm, ví dụ như bộ nghiệm: $(a,b,c,d)\sim (0,\frac{1}{2},1,\frac{1}{2})$

Như vậy ta có giá trị nhỏ nhất của $P$ là $\frac{3}{4}$, xảy ra chẳng hạn khi $(a,b,c,d)\sim (0,\frac{1}{2},1,\frac{1}{2})$.

Làm thế nào để có cách tách "kỳ diệu" như thế nhỉ

Bài 50 (Taiwan TST Round 2). Cho hai số thực dương $x,y$ thỏa mãn điều kiện $x+y=1.$ Chứng minh rằng
\[\frac{x}{x^2+y^3}+\frac{y}{x^3+y^2} \leqslant 2 \left(\frac{x}{x+y^2}+\frac{y}{x^2+y}\right).\]
 

Giải: Áp dụng bất đẳng thức Cauchy, ta có $(x^2+y^3)(1+y)\geq (x+y^2)^2>0$. Suy ra $\frac{x}{x^2+y^3}\leq \frac{x(1+y)}{(x+y^2)^2}$.

Tương tự ta có $\frac{y}{y^2+x^3}\leq \frac{y(1+x)}{(y+x^2)^2}$. Cộng vế theo vế với BĐT trên, ta có:

$\frac{x}{x^2+y^3}+\frac{y}{y^2+x^3}\leq \frac{x(1+y)}{(x+y^2)^2}+\frac{y(1+x)}{(y+x^2)^2}$.

Ta sẽ chứng minh $\frac{x(1+y)}{(x+y^2)^2}+\frac{y(1+x)}{(y+x^2)^2} \leq 2\left (\frac{x}{x+y^2}+\frac{y}{y+x^2} \right ) (1)$

Ta có:

$\frac{x(1+y)}{(x+y^2)^2}-\frac{2x}{x+y^2}=\frac{x}{x+y^2}\left ( \frac{1+y}{x+y^2}-2 \right )=\frac{x(1+y-2y^2-2x)}{(x+y^2)^2}=\frac{-x^2(x-y)}{(x+y^2)^2}$

$\frac{y(1+x)}{(y+x^2)^2}-\frac{2y}{y+x^2}=\frac{-y^2(y-x)}{(y+x^2)^2}$

$(1)\Leftrightarrow \frac{-x^2(x-y)}{(x+y^2)^2}+\frac{-y^2(y-x)}{(y+x^2)^2}\leq 0 \Leftrightarrow -(x-y)\left ( \frac{x^2}{(x+y^2)^2}-\frac{y^2}{(y+x^2)^2} \right )\leq 0\Leftrightarrow \frac{-(x-y)^2(x^2+xy+y^2)}{(x+y^2)(y+x^2)}\left ( \frac{x}{x+y^2}+\frac{y}{y+x^2} \right )\leq 0$ (đúng)

Từ đó ta có điều phải chứng minh. ĐTXR $\Leftrightarrow x=y=\frac{1}{2}$

Ý bạn là sao ? 

Do $B(x)$ có 2 nghiệm nên em không rõ là $Q(x)-(3x-1)$ có nhận số còn lại làm nghiệm hay không (em không rành lắm về đa thức). Nếu có, anh có thể chứng minh chặt chẽ luôn được không ạ ? 

Câu 1:

Ý tưởng là để ý x = 3 là điểm nhạy cảm của dãy số.

a)Ta chứng minh các bước sau

- $x_n>3 \forall n$

- $|x_{n+1}-3|<\frac{|x_n-3|}{2}$

b)Chia làm hai TH:

Nếu tồn tại $n$ để $x_n>3$ thì cmtt như a)

Xét $x_n<3 \forall n$

Chọn dãy $v_n = \frac{1}{2} + \sqrt{2u_n+\frac{1}{4}}$, ta có $u_n>v_n$ và $lim v_n = 3$, suy ra $lim x_n = 3$ do bị kẹp

 

Câu 2:

Tồn tại

Chọn $A(x) = (x-1)^3-2$, $B(X) = x^2 + 2x - 4$, ta có:

$gcd(A,B) = 1$, $P(x) - x$ chia hết cho $A(x)$ và $Q(x) - (3x-1)$ chia hết cho $B(x)$

Suy ra, ta cần tìm $P(x)$ thoả mãn:

$P = A.Q + x = B.R + (3x-1)$

$\Leftrightarrow A.Q - B.R = 2x-1$

Vì $gcd(A,B) = 1$ nên theo thuật chia Euclid, tồn tại $Q,R$ hệ số nguyên thoả mãn, suy ra dpcm

$Q(x)-(3x-1)$ chia hết cho $B(x)$ thì mọi nghiệm của $B(x)$ là mọi nghiệm của $Q(x)-(3x-1)$, nhưng tại sao lại thế vậy anh ?

Bài 5: Đẳng thức $(x-1)(x-2)...(x-2016)=(x-1)(x-2)...(x-2016)$ được viết trên bảng với 2016 thừa số ở mỗi vế. Xác định giá trị nhỏ nhất có thể của $k$ để ta có thể xoá $k$ trong số 4032 thừa số trên, với điều kiện là mỗi vế còn lại ít nhất một thừa số, để phương trình nhận được sau phép biến đổi là vô nghiệm.

Giải: Ta sẽ chứng minh rằng $k=2016$ là giá trị nhỏ nhất cần tìm.

Nếu như ta xoá ít hơn 2016 thừa số, thì đẳng thức nhận được chứa ít nhất 2017 thừa số. Do có 2016 loại thừa số là $x-1$, $x-2$,..., $x-2016$ nên theo nguyên lý Dirichlet, tồn tại một thừa số xuất hiện 2 lần. Thừa số ấy xuất hiện ở cả 2 vế của đẳng thức, dẫn đến việc phương trình nhận được sẽ có nghiệm. Do đó $k\geqslant 2016$

Xét phương trình $(x-1)(x-3)...(x-2015)=(x-2)(x-4)...(x-2016)$ $(1)$ nhận được sau khi xoá $k=2016$ thừa số từ đẳng thức ban đầu.

Trường hợp $x\in \left \{ 1;2;...;2016 \right \}$ thì phương trình hiển nhiên vô nghiệm.

Với $x< 1$ thì $2015-x<2016-x$ ,..., $1-x<2-x$. Cả 2 vế của các bất đẳng thức trên đều dương nên nhân vế theo vế, $VT(1)<VP(1)$. Phương trình vô nghiệm.

Với $1<x<2$ thì $VT(1)<0<VP(1)$ nên phương trình cũng vô nghiệm.

Với $2<x<3$ thì $2015-x<2016-x$ ,..., $3-x<4-x$, $x-1<x-2$. Cả 2 vế các BĐT trên đều dương nên nhân vế theo vế và đổi dấu, $VT(1)>VP(1)$. Phương trình vô nghiệm.

Với $3<x<4$ thì $VT(1)>0>VP(1)$ nên phương trình cũng vô nghiệm.

Các trường hợp còn lại ta chứng minh tương tự.

Kết luận: Giá trị nhỏ nhất của k là 2016.

Mình nghĩ lời giải này chưa đúng, vì sau khi khai triển hết ra thì hệ số của $x^{1008}$ triệt tiêu, so sánh hệ số của $x^{1007}$ 2 vế thì ta thấy $1+3+\ldots+2015< 2+4+\ldots+2016$, do đó đây là phương trình bậc $1007$ và có nghiệm thực. 

 

Lời giải của mình thì xét phương trình $\prod \limits_{i=0}^{503} (x-4i-1)(x-4i-4)=\prod \limits_{i=0}^{503}(x-4i-2)(x-4i-3)$ (1). 

Ta chứng minh rằng $VT(1)<VP(1)$. Chú ý rằng nếu $x<1$, $x>2016$ hoặc $4k<x<4k+1$ thì tất cả các giá trị $(x-4i-1)(x-4i-4)$ và $(x-4i-2)(x-4i-3)$ đều dương, do đó áp dụng bất đẳng thức $(x-4i-1)(x-4i-4)<(x-4i-2)(x-4i-3)$ với mọi $0 \leq i \leq 503$ ta suy ra đpcm.

Ngoài ra, nếu $4k+1<x<4k+2$ hay $4k+3<x<4k+4$ thì dễ thấy $VT(1)<0<VP(1)$. Như vậy ta chỉ cần xét trường hợp tồn tại $k$ sao cho $4k+2<x<4k+3$. Đến đây ta sử dụng bất đẳng thức khác $(x-4i-3)(x-4i-6)<(x-4i-4)(x-4i-5)$ (lúc này tất cả các giá trị $(x-4i-3)(x-4i-6)$ và $(x-4i-4)(x-4i-5)$ đều dương). (2)

Lưu ý là không như trường hợp ở trên, BDT này không quét hết được tất cả các giá trị, mà còn sót lại $(x-1)(x-1008)$ và $(x-2)(x-1007)$. Lúc này do tồn tại $k$ để $4k+2<x<4k+3$ nên $0>(x-2)(x-1007)>(x-1)(x-1008)$. Từ đó ta suy ra $0<\frac{(x-2)(x-1007)}{(x-1)(x-1008)}<1$. (3)

Từ (2) và (3) ta suy ra $0<\frac{VP(1)}{VT(1)}<1$. Tuy nhiên do $4k+2<x<4k+3$ nên cả $VT$ và $VP$ đều âm, từ đó ta suy ra $VT(1)<VP(1)$. 

Vậy $2016$ là giá trị cần tìm.

Đúng là em bị sai lầm ở đoạn "chứng minh tương tự" thật ! Em cảm ơn anh 

Các bài toán đều hay và đẹp ạ   

Em hy vọng tạp chí PI sẽ thành công như mong đợi   !

Bài 4:

Đánh thứ tự các cột từ trái sang phải.

Ta điền số vào tất cả các ô của bảng sao cho toàn bộ cột 1 là số 0, toàn bộ cột 2 là số 1, toàn bộ cột 3 là số 0... toàn bộ cột 99 là số 0.

Mỗi viên gạch đều che phủ phần diện tích có tổng các số được ghi trong các ô là chẵn.

Mà tổng các số được điền vào bảng là $49.99$ là số lẻ.

Vậy không thể lát bảng ô vuông như đề bài. 

Hoàn toàn có thể phủ được.

Do bảng khuyết ô trung tâm nên ta chia được bảng thành $4$ hình chữ nhật kích thước $44.45$. Mỗi hình chữ nhật như thế đều phủ được bởi các dải $44 $ đơn vị (dễ chỉ ra).