Câu 1: (2 điểm)
a/ Cho A = $\frac{2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}}{\sqrt{6}+\sqrt{2}}$, chứng minh A là một số nguyên.
b/ Giải hệ phương trình : $$\left\{\begin{array}{l}x^{2}=12y+6 \\2y^{2}=x-1 \end{array}\right.$$
Câu 2: (2 điểm)
a/ Cho (P): $y=\frac{1}{3}x^{2}$ và đường thẳng (d): $y=-x+\frac{4}{3}$. Gọi A, B là giao điểm của đường thẳng (d) và parabol (P), tìm điểm M trên trục tung sao cho độ dài MA +MB nhỏ nhất.
b/ Giải phương trình: $x^{2}+5x+8=3\sqrt{2x^{3}+5x^{2}+7x+6}$.
Câu 3: (2 điểm)
a/ Cho f(x) là một đa thức với hệ số nguyên. Biết f(1).f(2) = 2013, chứng minh phương trình f(x) = 0 không có nghiệm nguyên.
b/ Cho p là một số nguyên tố. Tìm p để tổng các ước nguyên dương của $p^{4}$ là một số chính phương.
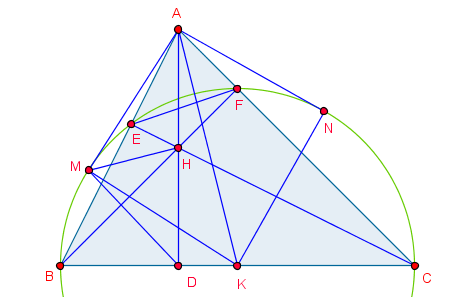
Câu 4: (3 điểm) Cho tam giác ABC có 3 góc nhọn (AB $<$ AC) nội tiếp đường tròn tâm O. Đường tròn (K) đường lính BC cắt các cạnh AB, AC lần lượt tại E và F. Gọi H là giao điểm của BF và CE.
a/ Chứng minh AE.AB = AF.AC.
b/ Chứng minh OA vuông góc với EF.
c/ Từ A dựng các tiếp tuyến AM, AN đến đường tròn (K) với M, N là các tiếp điểm. Chứng minh ba điểm M, H, N thẳng hàng.
Câu 5: (1,0 điểm) Cho các số a, b, c, d thỏa mãn điều kiện: ac - bd = 1. Chứng minh rằng:
$a^{2}+b^{2}+c^{2}+d^{2}+ad+bc \geq \sqrt{3}$
Bài viết đã được chỉnh sửa nội dung bởi Miranda: 27-06-2013 - 21:13