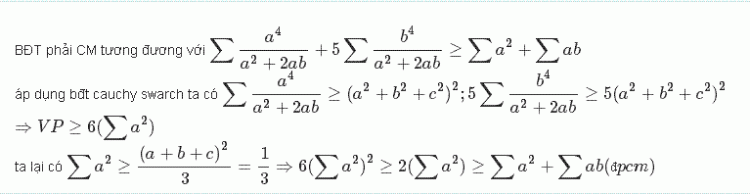Chủ đề này có 4 trả lời

[vutuanhien]

Ngày 1:

Câu 1:Cho tam giác đều $ABC$, $D$ là 1 điểm nằm trên cạnh $BC$ ($D$ không trùng với các đỉnh). Gọi $I$ là tâm đường tròn ngoại tiếp tam giác $ABD$ đối diện với cạnh $AB$, $J$ là tâm đường tròn bàng tiếp tam giác $ACD$ đối diện với cạnh $AC$. Giả sử $E$ là giao điểm thứ 2 của đường tròn ngoại tiếp các tam giác $ABI$ và tam giác $ẠCJ$. Chứng minh rằng:$A$ là tâm đường tròn nội tiếp tam giác $IEJ$

Câu 2:

1. Tìm tất cả các số nguyên tố $p,q,r$ thỏa mãn $p+q+r$ không chia hết cho 3; $p+q+r$ và $p+q+r+3$ đều là các số chính phương
2. Có tồn tại các số nguyên tố $p,q,r$ thỏa mãn $p+q+r$ chia hết cho 3; $p+q+r$ và $p+q+r+3$ đều là các số chính phương

Câu 3:Hai bạn $A$ và $B$ cùng chơi 1 trò chơi gồm 1 quả bóng và $n$ cái hộp được đặt trên các đỉnh của 1 đa giác lồi có $n$ cạnh ($n$ là 1 số nguyên dương). Đầu tiên $A$ giấu quả bóng vào 1 chiếc hộp. Ở mỗi lượt chơi, $B$ sẽ chọn 1 hộp bất kì và $A$ sẽ nói khoảng cách từ quả bóng đến chiếc hộp vừa được chọn, và sau đó chuyển quả bóng sang hộp liền kề. Nếu $B$ tìm ra được quả bóng thì $B$ thắng. Tìm số lượt chơi ít nhất để $B$ chắc chắn thắng trò chơi

Câu 4:Với mọi số thực $a,b,c$ thỏa mãn $a+b+c=1$, chứng minh rằng:

$$\frac{a^4+5b^4}{a(a+2b)}+\frac{b^4+5c^4}{b(b+2c)}+\frac{c^4+5a^4}{c(c+2a)}\geq 1-ab-bc-ca$$

Ngày 2:

Câu 5:Cho $a,b,c,d$ là các số thực lớn hơn $1$ và $x,y$ là các số thực dương thỏa mãn 

$$a^{x}+b^{y}=(a^2+b^2)^{x}$$ và $$c^{x}+d^{y}=2^{y}(cd)^{\frac{y}{2}}$$

Chứng minh rằng:$x< y$

Câu 6:Tìm tất cả các số nguyên dương $n$ thỏa mãn $n!+1\vdots 2n+7$

Câu 7:Cho tứ giác lồi $ABCD$, 2 đường chéo cắt nhau tại $E$ và $BE=\sqrt{2}.DE$; $\angle BEC=45^{\circ}$. Gọi $F$ là chân đường cao hạ từ $A$ xuống $BC$ và $P$ là giao điểm thứ 2 của đường tròn ngoại tiếp tam giác $BFD$ và đoạn thẳng $DC$. Tính số đo góc $\angle APD$

Câu 8:Trong một đồ thị có hướng với $2013$ đỉnh, có đúng 1 cạnh giữa bất kì hai đỉnh và với mọi đỉnh, tồn tại một cạnh không chứa đỉnh đó. Biết rằng, với mọi cách sắp xếp các cạnh, từ mỗi cạnh chúng ta có thể tiến tới $k$ đỉnh khác bằng cách dùng tối đa 2 cạnh. Tìm giá trị lớn nhất của $k$

Lưu ý:Không thảo luận tại đây mà nhấn vào từng bài để thảo luận

Bài viết đã được chỉnh sửa nội dung bởi vutuanhien: 10-07-2013 - 11:05

[ngoctruong236]

$Lời giải. a) \blacktriangleright Nếu p,q,r đều lẻ thì 4 \nmid p+q+r, do đó p+q+r \equiv 1 \pmod{4} (vì p+q+r là số chính phương). Để thỏa mãn các yếu cầu trên thì số dư của p,q,r khi chia cho 4 phải là 1,3,1 hoặc 3,3,3 (vì p,q,r lẻ nên chỉ có thể chia 4 dư 1 hoặc 3).Với trường hợp p,q,r khi chia cho 4 nhận số dư là 1,3,1 thì pq+pr+rp+3 chia 4 dư 2, mâu thuẫn vì pq+qr+rp+3 chính phương. Với trường hợp p,q,r khi chia cho 4 nhận số dư là 3,3,3 thì pq+pr+rp+3 chia 4 dư 2, mâu thuẫn vì pq+qr+rp+3 chính phương.Vậy trong ba số nguyên tố p,q,r có ít nhất một số chẵn, tức có ít nhất một số là 2. Không mất tính tổng quát, giả sử p=2. \blacktriangleright Nếu q,r không có số nào chia hết cho 3, mà 2+q+r \equiv 1 \pmod{3} suy ra khi q,r chia 3 có thể nhận số dư là 1,1. Tuy nhiên khi đó thì pq+qr+rp+3 sẽ chia 3 dư 2, mâu thuẫn vì pq+qr+rp+3 chính phương. Do đó trong hai số q,r phải có một số chia hết cho 3, tức có một số bằng 3. Giả sử q=3. \blacktriangleright Ta có pq+qr+rp+3=9+5r là số chính phương nên ta đặt 9+5r=b^2 \Leftrightarrow (b-3)(b+3)=5r với b \in \mathbb{N}^*. Vì r nguyên tố nên dễ dàng tìm được r=11. Kết luận. Vậy ba số nguyên tố cần tìm là 2,3,11.$

[ngoctruong236]

$b) Câu trả lời là có. Theo lập luận câu a thì có thể giả sử p=2. Đến đây chắc là thử chọn thì có cặp 2,11,23 thỏa mãn.$.Đay la loi giai bai 2 cua toi

[Ha Manh Huu]

sao ko ai giải nhỉ mà cái bài bđt có trên face rồi 

 

Hình gửi kèm

• 

[cool hunter]

 

Ngày 1:

Câu 1:Cho tam giác đều $ABC$, $D$ là 1 điểm nằm trên cạnh $BC$ ($D$ không trùng với các đỉnh). Gọi $I$ là tâm đường tròn ngoại tiếp tam giác $ABD$ đối diện với cạnh $AB$, $J$ là tâm đường tròn bàng tiếp tam giác $ACD$ đối diện với cạnh $AC$. Giả sử $E$ là giao điểm thứ 2 của đường tròn ngoại tiếp các tam giác $ABI$ và tam giác $ẠCJ$. Chứng minh rằng:$A$ là tâm đường tròn nội tiếp tam giác $IEJ$

Câu 2:

1. Tìm tất cả các số nguyên tố $p,q,r$ thỏa mãn $p+q+r$ không chia hết cho 3; $p+q+r$ và $p+q+r+3$ đều là các số chính phương
2. Có tồn tại các số nguyên tố $p,q,r$ thỏa mãn $p+q+r$ chia hết cho 3; $p+q+r$ và $p+q+r+3$ đều là các số chính phương

 

Hình như đề là I là tâm đường tròn bàng tiếp mới đúng.

Còn câu 2 chính xác phải là:

Câu 2:

1. Tìm tất cả các số nguyên tố $p,q,r$ thỏa mãn $p+q+r$ không chia hết cho 3; $p+q+r$ và $pq+qr+rp+3$ đều là các số chính phương
2. Có tồn tại các số nguyên tố $p,q,r$ thỏa mãn $p+q+r$ chia hết cho 3; $p+q+r$ và $pq+qr+rp+3$ đều là các số chính phương

Bài viết đã được chỉnh sửa nội dung bởi cool hunter: 09-08-2013 - 20:44