Trung sĩ
Định lý: Tâm của các đường tròn đi qua ba đỉnh của tam giác và tiếp xúc các trung tuyến tương ứng của các đỉnh còn lại tại trọng tâm tam giác nằm trên một đường tròn.
Đường tròn đó gọi là đường tròn Đào, tâm đường tròn đó được đánh số là X(5569) trong từ điển ETC
Từ điển ETC là một từ điển toán học nguồn, rất nổi tiếng đối với nền toán học cơ bản.
http://faculty.evans...a/ETCPart4.html
Edited by khongghen, 07-11-2013 - 13:25.
$LOVE(x)|_{x =\alpha}^\Omega=+\infty$
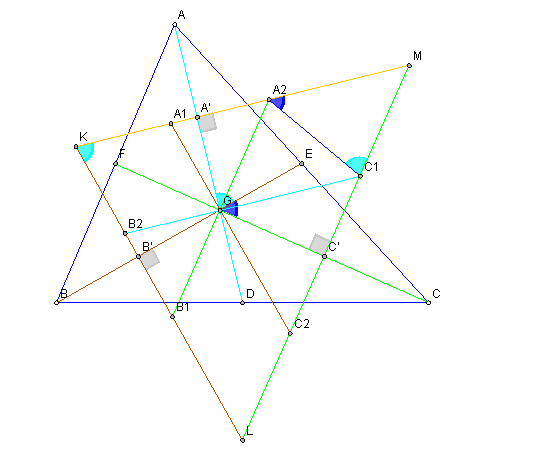
Bài toán:
Cho $\triangle ABC$ và trọng tâm $G$. Gọi $(A_b)$ là đường tròn qua $A,G$ và tiếp xúc $GB$. Gọi $(A_c)$ là đường tròn qua $A,G$ và tiếp xúc $GC$. Xác định $(B_a),(B_c),(C_a),(C_b)$ tương tự.
Chứng minh rằng $A_b,A_c,B_c,B_a,C_a,C_b$ đồng viên.
Lời giải:
Kí hiệu $[\pi]$ nghĩa là $\pmod {\pi}$
Trước hết, ta cần có 2 bổ đề sau:
Bổ đề 1: Cho $\triangle ABC$. Gọi $(O_1)$ là đường tròn qua $A,C$ và tiếp xúc $AB$. Gọi $(O_2)$ là đường tròn qua $A,B$ và tiếp xúc $AC$. $D$ là giao điểm thứ 2 của $(O_1),(O_2)$. Khi đó $AD$ là đường đối trung $\triangle ABC$.
Chứng minh bổ đề 1:
Do cách dựng nên $D,B$ cùng phía so với $AC$; $D,C$ cùng phía so với $AB$. Từ đó suy ra $D \in \angle BAC$.
Ta có $\angle DBA=\angle DAC$ và $\angle DAB=\angle DCA \Rightarrow \triangle DBA \sim \triangle DAC \Rightarrow \dfrac{d(D,AB)}{d(D,AC)}=\dfrac{AB}{AC}$
Đẳng thức cuối cho ta: $D$ nằm trên đường đối trung ứng đỉnh $A$ của $\triangle ABC$. Ta có đpcm.
=============================
Bổ đề 2: Cho 3 đường tròn $(O_1),(O_2),(O_3)$ có các trục đẳng phương của $d_1,d_2,d_3$. Giả sử $d_1,d_2,d_3$ tạo thành 1 tam giác thì khi đó $(O_1)\equiv (O_2) \equiv (O_3)$.
=============================
Quay lại bài toán. Đầu tiên, ta sẽ chứng minh tồn tại đường tròn $(\gamma_a)$ để $B_a,B_c,C_a,C_b \in (\gamma_a)$.
Thật vậy, gọi $A'$ là trung điểm $BC$, $D$ là giao điểm thứ 2 của $(B_c),(C_b)$.
\[
\begin{array}{l}
\left. \begin{array}{l}
C_a B_a \bot GA' \\
C_a C_b \bot GC \\
\end{array} \right\} \Rightarrow \left( {C_a B_a ,C_a C_b } \right) \equiv \left( {GA',GC} \right)[\pi] \\
\left. \begin{array}{l}
B_c B_a \bot GB \\
B_c C_b \bot GD \\
\end{array} \right\} \Rightarrow \left( {B_c B_a ,B_c C_b } \right) \equiv \left( {GB,GD} \right)[\pi] \\
\end{array}
\]
Mặt khác, theo bổ đề 1 cho $\triangle GBC$, ta có $GD$ là đường đối trung của $\triangle GBC$ nên\[
\left( {GB,GD} \right) \equiv \left( {GA',GC} \right)[\pi] \Rightarrow \left( {C_a B_a ,C_a C_b } \right) \equiv \left( {B_c B_a ,B_c C_b } \right)[\pi] \Rightarrow C_a ,C_b ,B_a ,B_c \in \left( {\gamma _a } \right)
\]
Chứng minh tương tự, ta có $A_b,A_c,B_c,B_a \in (\gamma_c)$ và $A_b,A_c,C_a,C_b \in (\gamma_b)$.
Mặt khác, $(\gamma_a),(\gamma_b),(\gamma_c)$ có các trục đẳng phương của $A_bA_c,B_cB_a,C_aC_b$: trung trực của $GA,GB,GC$ nên các trục đẳng phương đó tạo thành 1 tam giác. Áp dụng bổ đề 2, ta có $$(\gamma_a)\equiv(\gamma_b)\equiv (\gamma_c)$$
Ta có đpcm.
Edited by perfectstrong, 13-11-2013 - 19:19.
Trung sĩ
Edited by khongghen, 16-11-2013 - 18:00.
$LOVE(x)|_{x =\alpha}^\Omega=+\infty$
Định lý: Tâm của các đường tròn đi qua ba đỉnh của tam giác và tiếp xúc các trung tuyến tương ứng của các đỉnh còn lại tại trọng tâm tam giác nằm trên một đường tròn.
Đường tròn đó gọi là đường tròn Đào, tâm đường tròn đó được đánh số là X(5569) trong từ điển ETC
Từ điển ETC là một từ điển toán học nguồn, rất nổi tiếng đối với nền toán học cơ bản.
http://faculty.evans...a/ETCPart4.html
Bài toán:
Cho $\triangle ABC$ và trọng tâm $G$. Gọi $(A_b)$ là đường tròn qua $A,G$ và tiếp xúc $GB$. Gọi $(A_c)$ là đường tròn qua $A,G$ và tiếp xúc $GC$. Xác định $(B_a),(B_c),(C_a),(C_b)$ tương tự.
Chứng minh rằng $A_b,A_c,B_c,B_a,C_a,C_b$ đồng viên.
Ta có 2 nhận xét sau (do Peter Moses đề xuất)
Nhận xét 1: $$B_cC_b=C_aA_c=A_bB_a$$
Nhận xét 2: Gọi $X$ là tâm của đưòng tròn qua $A_b,A_c,B_c,B_a,C_a,C_b$. Gọi $\alpha$ là góc Brocard trong $\triangle ABC$.
Khi đó: $$\angle A_bB_aX=\angle B_cC_bX=\angle C_aA_cX=\dfrac{\pi}{2}-\alpha$$
==============================
Nhận xét 1 đúng vì $A_bC_b \parallel B_aB_c$ nên $B_aA_b=B_cC_b$. Tương tự: $B_aA_b=A_cC_a$.
Thậm chí, ta cũng có thể tình được $B_cC_b$ như sau:
Dựng hình bình hành $AG_bCG$. Ta có:\[
\begin{array}{l}
\left. \begin{array}{l}
\angle GB_c B = 2\angle C'GB = 2\angle CGB' = \angle CC_b G \\
\frac{{B_c G}}{{B_c B}} = 1 = \frac{{C_b G}}{{C_b C}} \\
\end{array} \right\} \Rightarrow \triangle GB_c B \sim \triangle GC_b C\left( {c.g.c} \right) \\
\left. \begin{array}{l}
\Rightarrow \frac{{GB_c }}{{GC_b }} = \frac{{GB}}{{GC}} = \frac{{GG_b }}{{AG_b }} \\
\angle B_c GC_b = 90^o - \angle C_b GC = \angle CGB' = \angle AG_b G \\
\end{array} \right\} \Rightarrow \triangle GB_c C_b \sim \triangle G_b GA\left( {c.g.c} \right) \\
\Rightarrow \frac{{B_c C_b }}{{GA}} = \frac{{GB_c }}{{G_b G}} = \frac{{\frac{{GB}}{{2\sin GDB}}}}{{GB}} = \frac{1}{{2\sin BGC'}} = \frac{1}{{2\sin BGC}} \\
\Rightarrow B_c C_b = \frac{{GA}}{{2\sin BGC}} = \frac{{GA}}{{2.\frac{{2S_{BGC} }}{{GB.GC}}}} = \frac{{GA.GB.GC}}{{4S_{BGC} }} = \frac{3}{4}.\frac{{GA.GB.GC}}{{S_{ABC} }} \\
\end{array}
\]
=================================
Ngoài ra, ta còn 1 nhận xét sau:
Gọi $A_0,B_0,C_0$ là tâm ngoại tiếp $\triangle GBC,GCA,GAB$. 1 tính chất quen thuộc đó là: $G$ là điểm Lemoine của $\triangle A_0B_0C_0$. Từ đó, ta thấy đường tròn $(X)$ qua $B_c,C_b,C_a,A_c,A_b,B_a$ chính là đường tròn Lemoine thứ nhất của $\triangle A_0B_0C_0$
Edited by perfectstrong, 15-11-2013 - 22:25.
Binh nhất
Một cách chứng minh khác cho Dao's circle:
Gọi $K, L, M$ là giao điểm của các đường trung trực của $AG, BG, CG$ (xem hình vẽ), tâm của các đường tròn được nói tới là $A_{1}, A_{2}, B_{1}, B_{2}, C_{1},C_{2}$. Do tứ giác $A’MC’G$ là tứ giác nội tiếp nên $\angle DGC’ = \angle A’MC’$ hay là $\angle AGE + \angle EGC = \angle MA_{2}C_{1} + \angle A_{2}C_{1}M$ (1)
Lưu ý là $\Delta GC’C_{1}\sim \Delta GA’A_{2}$ và vì $E$ là trung điểm của $AC$ nên
$sin AGE/sin EGC = GC/GA = GC’/GA’ = GC_{1}/GA_{2} = MC_{1}/MA_{2} = sin MA_{2}C_{1}/sin\angle A_{2}C_{1}M$ (2)
(1) và (2) cho $\angle AGE = \angle A_{2}C_{1}M$ nhưng dễ thấy $\angle AGE =\angle MKL$ nên tứ giác $KA_{2}C_{1}L$ là tứ giác nội tiếp, do $A_{1}C_{2}\parallel KL$ nên $A_{1}A_{2}C_{1}C_{2}$ là tứ giác nội tiếp.
Làm tương tự như trên hai lần nữa sẽ thấy sáu điểm $A_{1}, A_{2}, B_{1}, B_{2}, C_{1},C_{2}$ quả thực nằm trên một đường tròn.
Edited by malx, 17-11-2013 - 02:50.
Trung sĩ
Thân chào malx nhớ ngày xưa khi mới tham gia diễn đàn này, lúc đó chưa quen ai mà chỉ quen cậu, cậu giúp tớ dịch một bài sang tiếng Anh. Đến nay gặp lại như gặp lại cố nhân, rất hân hạnh. Mời cậu tham khảo: http://www.artofprob...p?f=47&t=554776
Đào Thanh Oai
Edited by khongghen, 18-11-2013 - 23:06.
Binh nhất
@khongghen: Cám ơn bạn nhé, chúc bạn nhiều thành công! 
Edited by malx, 19-11-2013 - 00:58.
Trung sĩ
Định lý tổng quát đã được đề cập tại đây từ năm 2012
http://groups.yahoo....s/messages/5612
https://groups.googl...ege/bEVpuj-gDNM
Edited by khongghen, 05-01-2014 - 13:31.
0 members, 1 guests, 0 anonymous users
Community Forum Software by IP.Board
Licensed to: Diễn đàn Toán học
