Chủ đề này có 7 trả lời

[Dream com true]

Cho tam giác nhọn ABC nội tiếp (O) và ngoại tiếp (I). M, N là điểm chính giữa của cung nhỏ AB, AC. G là điểm thuộc cung ngỏ BC. Gọi I' và I'' là tâm đường trọn nội tiếp các tam giác ABG, ACG. Đường tròn ngoại tiếp tam giác GI'I'' cắt (O) tai P. CMR P, I và trung điểm MN thằng hàng 

 

[nguyenthehoan]

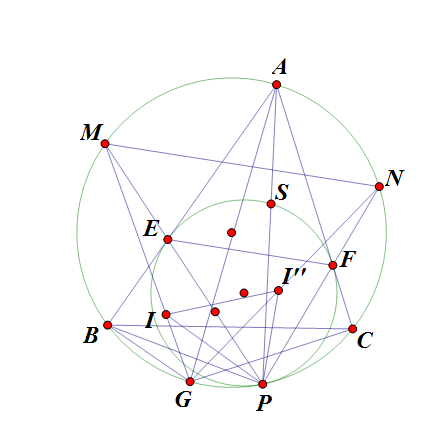
Cho tam giác nhọn ABC nội tiếp (O) và ngoại tiếp (I). M, N là điểm chính giữa của cung nhỏ AB, AC. G là điểm thuộc cung ngỏ BC. Gọi I' và I'' là tâm đường trọn nội tiếp các tam giác ABG, ACG. Đường tròn ngoại tiếp tam giác GI'I'' cắt (O) tai P. CMR P, I và trung điểm MN thằng hàng 

 

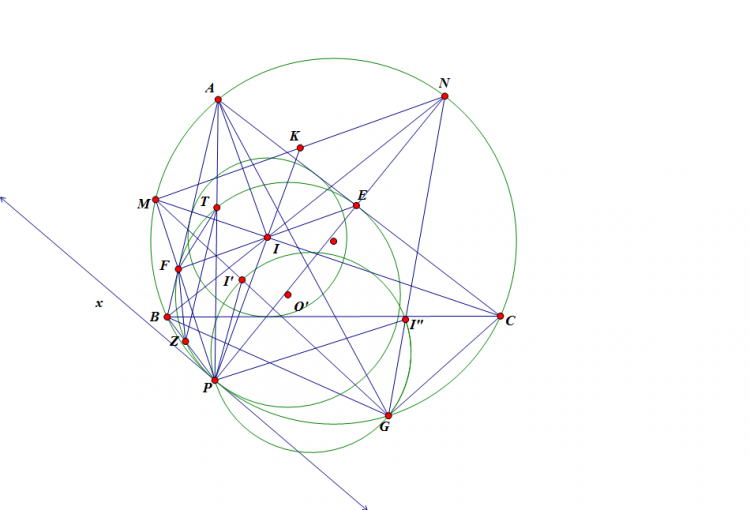
Gọi $P$ là tiếp điểm của đường tròn A-Mixtilinear với $(ABC)$.  (kí hiệu ($O'$) là đường tròn A-mixtilinear)

 

Ta sẽ chứng minh tứ giác $GPI'I"$ nội tiếp.

 

Gọi $E,F$ thứ tự là tiếp điểm của đường tròn $(O')$ trên $AC,AB$.

 

Gọi $Z,T$ thứ tự là giao điểm của $PB,PA$ với $(O')$.Qua $P$ vẽ tiếp tuyến $Px$ với $(O')$ (cũng là tiếp tuyến với $(O)$)

 

Khi đó vì $P$ là tâm vị tự trong của $(O)$ và $(O')$ nên $ZT//AB$

 

ta có $O'F\perp AB\Rightarrow O'F\perp ZT\Rightarrow FZ=FT$.Do đó $\widehat{FPZ}=\widehat{FBT}$

 

Vậy $PF$ đi qua trung điểm cung $AB$, hay $P,F,M$ thẳng hàng. Tương tự $P,E,N$ thẳng hàng.

 

Vì $I'$ là tâm nội tiếp $\Delta GAB$ nên $MI'=MA=MB$  (kết quả quen thuộc) tương tự $NI"=NA=NC$)

 

Ta có $\widehat{FPx}=\widehat{FEP}=\widehat{MNP}$ (vì $Px$ là tiếp tuyến của $(O)$ và $(O')$)

 

Nên $FE//MN$ $\Rightarrow \frac{MF}{MP}=\frac{NE}{NP}$  (1)

 

Lai có $\Delta MFA\sim \Delta MAP\Rightarrow MA^{2}=MF.NP$

 

Tương tự $NA^{2}=NE.NP$ $\Rightarrow \frac{MF.MP}{NE.NP}=\frac{MA^{2}}{NA^{2}}$  (2)

 

Từ (1) và (2) ta có $\frac{MA}{NA}=\frac{MP}{NP}=\frac{MI'}{NI"}$

 

Lạ có $\widehat{PMI'}=\widehat{PNI"}\Rightarrow \Delta PI'M\sim \Delta PI"N$ 

 

$\Rightarrow \widehat{I'PM}=\widehat{I"PN}\Rightarrow \widehat{I'PI"}=\widehat{MPN}=\widehat{I'GI"}$

 

Do đó tứ giác $GPI'I"$ nội tiếp.

 

Vậy ta có ngay giao điểm của $(GI'I")$ với $(O)$ cũng chính là tiếp điểm của đường tròn A_Mixtilinear với $(O)$.

 

Mặt khác ta có $MA=MI, NA=NI$ nên $MN\perp AI$, hay $MN//EF$.

 

Mà, $IE=IF$ nên $PI$ đi qua trung điểm của $MN$.

 

Vậy ta có điều phải chứng minh.

Bài viết đã được chỉnh sửa nội dung bởi nguyenthehoan: 08-12-2013 - 12:13

[haitienbg]

Mình có cách khác như sau (cũng gần giống với Hoàn nhưng theo chiều thuận hơn):

Bài viết đã được chỉnh sửa nội dung bởi haitienbg: 04-12-2013 - 21:58

[haitienbg]

Ta có $(C,I,M)$ và $(B,I,N)$ là các cặp thẳng hàng. Gọi $E,F$ thứ tự là giao của các cặp đt $(PM,AB), (PN,AC)$

có ngay hai tam giác $MI'P,NI''P$ đồng dạng (g-g) nên

$\frac{PM}{PN}=\frac{MI'}{NI''}=\frac{MB}{NC}$

 

$\Rightarrow \frac{PM^2}{PN^2}=\frac{MB^2}{NC^2}=\frac{ME.MP}{NF.NP}$

 

$\Rightarrow \frac{PM}{PN}=\frac{ME}{NF}$ hay $EF,MN$ s.song

 

Mà $IA,MN$ vuông góc nên $EF$ vuông góc với $AI$

$Pascal$ cho 6 điểm $P,M,C,A,B,N$ được $E,I,F$ thẳng hàng

Do đó $I$ là trung điểm của $EF$

Gọi $K$ là trung điểm của $MN$ ta có $K,I,P$ là thẳng hàng $\Rightarrow$ Dpcm~~.

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi haitienbg: 04-12-2013 - 21:59

[Ndtt]

T là trung điểm cung lớn BC . Dễ thấy IMTN là hbh => I , T , K thẳng hàng cắt ( O ) tại P' . 

I'M = IM = NT , I''N = IN = MT (1)

( TN . P'N ) / ( TM . P'M ) = KN/KM = 1 (2)

(1) , ( 2 ) => tg P'MI' đồng dạng tg P'NI'' => GI'I''P' là tgnt => P trùng P'

P/s : Đăng xog mới phát hiện ra cách làm trên cũng gần giống về ý tưởng . Ngại quá :|

Bài viết đã được chỉnh sửa nội dung bởi Ndtt: 05-12-2013 - 15:33

[thukilop]

 

di qua trung diem.png

 

 

 

Từ (1) và (2) ta có $\frac{MA}{NA}=\frac{MX}{NX}=\frac{MI'}{NI"}$

 

Lạ có $\widehat{PMI'}=\widehat{PNI"}\Rightarrow \Delta PI'M\sim \Delta PI"N$ 

Chỗ này mình chưa hiểu lắm, X,Y là điểm gì vậy, mà sao từ (1) và (2) lại suy ra được hệ thức này vậy  

[nguyenthehoan]

Chỗ này mình chưa hiểu lắm, X,Y là điểm gì vậy, mà sao từ (1) và (2) lại suy ra được hệ thức này vậy  

$X$ là $P$ nhé..Mình nhầm tí.Mình fix lại rồi. Còn chỗ bạn nói chỉ cần chia hai vế của (1) với (2) là được mà.

[BlackSelena]

Cho tam giác nhọn ABC nội tiếp (O) và ngoại tiếp (I). M, N là điểm chính giữa của cung nhỏ AB, AC. G là điểm thuộc cung ngỏ BC. Gọi I' và I'' là tâm đường trọn nội tiếp các tam giác ABG, ACG. Đường tròn ngoại tiếp tam giác GI'I'' cắt (O) tai P. CMR P, I và trung điểm MN thằng hàng 

Một cách khác nữa (càng nhiều càng tốt nhỉ ).

Dựng trước điểm $P$ ra, ta sẽ chứng minh $GII'I'P:tgnt$, mệnh đề này có vẻ tự nhiên hơn nhiều mà khúc sau trở đi lại rất dễ .

Và điều này tương đương với $\triangle MIP \sim \triangle NI''P$

$\Leftrightarrow \dfrac{MI}{MP} = \dfrac{NI''}{NP}$

$\Leftrightarrow \dfrac{MA}{MP} = \dfrac{NA}{NP}$

$\Leftrightarrow \dfrac{ES}{EP} = \dfrac{FS}{FP}$ (với $S$ là giao của $AP$ với đường tròn A-mixtilinear, chú ý thêm là $ES \parallel MA, FS \parallel NA$)

$\Leftrightarrow SEPF$ là tứ giác điều hòa. Điều này hiển nhiên đúng.

Vậy $G,I,I'',P$ đồng viên, chỗ còn lại khá là dễ dàng .

Mà từ đây ta có một bài toán khác như sau:
Cho tam giác $ABC$ nội tiếp $(O)$. Điểm $G$ bất kì trên cung $BC$ không chứa $A$. Gọi $I_1$ và $I_2$ là tâm nội tiếp của $\triangle ABG, \triangle ACG$. Khi đó ta có $GI_1I_2$ luôn đi qua 1 điểm cố định.

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 09-12-2013 - 01:58