TRƯỜNG ĐẠI HỌC KHOA HỌC TỰ NHIÊN
TRƯỜNG THPT CHUYÊN KHTN
ĐỀ THI OLYMPIC CHUYÊN KHOA HỌC TỰ NHIÊN 2014
Thời gian : 180 phút
NGÀY THỨ NHẤT
Câu I : Tìm tất cả các bộ ba số $(x,n,p)$ với $x,n$ là các số nguyên dương và $p$ là số nguyên tố thỏa mãn :
$$x^3+2x=3(p^n-1)$$
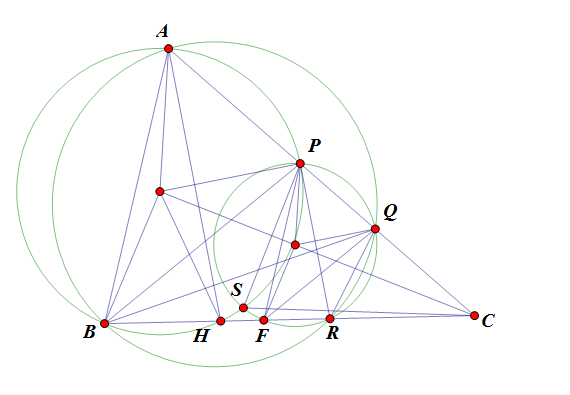
Câu II : Cho tam giác $ABC$. Trên đoạn thẳng $AC$ lấy điểm $P$ và trên đoạn thẳng $PC$ lấy điểm $Q$ sao cho $\dfrac{PA}{PC}=\dfrac{QP}{QC}$. Đường tròn ngoại tiếp tam giác $ABQ$ cắt $BC$ tại $R$ khác $B$.
a) Chứng minh rằng $\angle ABP=\angle PRQ$
b) Gọi $S$ là giao điểm khác $P$ của hai đường tròn ngoại tiếp các tam giác $PAB,PQR$. Chứng minh tam giác $CPS$ cân.
Câu III : Cho các số thực không âm $a,b,c,$ thỏa :
$$(a+b+2c)(b+c+2a)(c+a+2b)=1$$
Chứng minh rằng :
$$\dfrac{a}{b(4c+15)(b+2c)^2}+\dfrac{b}{c(4a+15)(c+2a)^2}+\dfrac{c}{a(4b+15)(a+2b)^2}\geq \dfrac{1}{3}$$
Vạn sự khởi đầu nan... :'(
Edited by Juliel, 23-05-2014 - 12:21.