Đã có số Tuần 1 tháng 9. Lời giải bài trước đã có trên số. Cách biến đổi tỉ số để chứng minh $\angle KNL=90^{\circ}$ trong lời giải này rất hay. 
Bài 3. Cho tam giác $ABC$ có đường tròn nội tiếp $(I)$ tiếp xúc $BC$ tại $D$. Tâm đường tròn bàng tiếp góc $A$ là $J$. $P$ là một điểm bất kì trên $(I)$ không trùng $D$. $Q$ thuộc $BC$ sao cho $JQ \parallel PD$. Chứng minh rằng đường tròn ngoại tiếp tam giác $PBC$ chia đôi $QJ$.
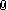 Screen Shot 2015-08-31 at 7.17.57 am.png
Screen Shot 2015-08-31 at 7.17.57 am.png
$JD$ cắt $(I)$ tại K,tiếp tuyến tại $K$ cắt $BC$ ở $T$, $TI$ cắt $JK$ tại $N$
ta có $TI.TN=TB.TC=TD^{2}=TK^{2}$
$T$ thuộc trục đẳng phương của $(I)$ và $(BPC)$
$(I)$ cắt lại $(PBC)$ tại $H$
ta có $H,P,T$ thẳng hàng
ta sẽ cm $M,D,H$ thẳng hàng
thật vậy ta có $D(QJPM)=-1$ (1)
lại có $PKHD$ điều hòa nên $D(DKPH)=-1$(2)
Từ (1) và (2) ta có $M,D,H$ thẳng hàng
Kẻ $MX$ vuông góc $BC$, $IY$ vuông góc $DH$
ta có $\triangle MDX$ đồng dạng với $\triangle IDY$
$\Rightarrow DM.DY=ID.MX\Rightarrow DM.DH=r.R_{a}$
ta chỉ cần cm $r.R_{a}= DB.DC$
Thật vậy qua $J$ kẻ $JE$ vuông góc $BC$ ta có
$\triangle IBD\sim \triangle BEJ$
$\Rightarrow ID.JE=BD.BE=BD.DC$ (DPCM)
![]()









