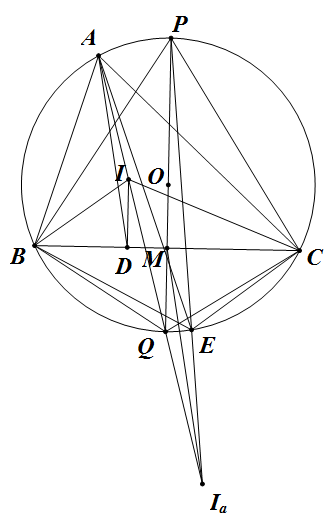
Cho $\bigtriangleup ABC $ nội tiếp đường tròn $(O)$, đường tròn nội tiếp $(I)$ tiếp xúc với $BC$ tại $D$. Đường tròn $ \textrm{A-mixtilinear excircle}$ ( đường tròn tiếp xúc ngoài với $(O)$ và tiếp xúc với các tia $AB, AC$) tiếp xúc ngoài với $(O)$ tại $E$. Chứng minh rằng $AD, AE$ đẳng giác trong góc $A$.
#2
Đã gửi 11-06-2016 - 21:08
viet nam in my heart
-
- Điều hành viên OLYMPIC
-
- 242 Bài viết
Thượng sĩ
Gọi $M$ là trung điểm $BC$.
$P,Q$ lần lượt là điểm chính giữa các cung $BC$ chứa $A$ và không chứa $A$
$I_a$ là tâm đường tròn bàng tiếp góc $A$ của tam giác $ABC$
Trước hết ta có $3$ bổ đề khá quen thuộc sau
Bổ đề 1: $EI_a$ là phân giác của góc $\widehat{BEC}$. (Chứng minh tương tự định lý với đường tròn mixtilinear-incircle)
Bổ đề 2(quen thuộc): $Q$ là trung điểm của $II_a$
Bổ đề 3(quen thuộc): $I_aM \parallel AD$
Trở lại bài toán:
Áp dụng bổ đề $3$ thì để chứng minh $AD,AE$ đẳng giác trong góc $A$ thì ta quy về chứng minh: $\widehat{QI_aM}=\widehat{MPI_a}$
Hay ta chỉ cần chứng minh: $QI_a$ là tiếp tuyến của $(MPI_a)$ $\Leftrightarrow QI_{a}^2 = QM.QP$
Theo bổ đề $2$ thì chỉ cần chứng minh $QI^2=QM.QP\Leftrightarrow QB^2=QM.QB$(đúng theo hệ thức lượng trong tam giác vuông $QBP$) $\blacksquare$
.
Bài viết đã được chỉnh sửa nội dung bởi viet nam in my heart: 30-06-2016 - 11:19
- anhquannbk yêu thích
"Nếu bạn hỏi một người giỏi trượt băng làm sao để thành công, anh ta sẽ nói với bạn: ngã, đứng dậy là thành công." Isaac Newton
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh
