Cho a,b,c là các số thực dương. CMR: $\sum \frac{2a}{b+c}\geq 3+\frac{(a-b)^2+(b-c)^2+(c-a)^2}{(a+b+c)^2}$

Cho a,b,c là các số thực dương. CMR: $\sum \frac{2a}{b+c}\geq 3+\frac{(a-b)^2+(b-c)^2+(c-a)^2}{(a+b+c)^2}$
#1
 Đã gửi 20-04-2017 - 20:08
Đã gửi 20-04-2017 - 20:08

Làm việc đừng quá trông đợi vào kết quả, nhưng hãy mong cho mình làm được hết sức mình
#2
 Đã gửi 20-04-2017 - 20:30
Đã gửi 20-04-2017 - 20:30

Cho a,b,c là các số thực dương. CMR: $\sum \frac{2a}{b+c}\geq 3+\frac{(a-b)^2+(b-c)^2+(c-a)^2}{(a+b+c)^2}$
Bài viết đã được chỉnh sửa nội dung bởi Mr Cooper: 20-04-2017 - 21:08
- yeutoan2001, NHoang1608 và monkeyking thích
#3
 Đã gửi 20-04-2017 - 21:15
Đã gửi 20-04-2017 - 21:15

Ta có:
\[\sum\limits_{cyc} {\frac{{2a}}{{b + c}}} - 3 - \frac{{\sum\limits_{cyc} {{{\left( {a - b} \right)}^2}} }}{{{{\left( {a + b + c} \right)}^2}}} = \sum\limits_{cyc} {{{\left( {a - b} \right)}^2}\left( {\frac{{{a^2} + {b^2} + ab + bc + ca}}{{\left( {a + c} \right)\left( {b + c} \right){{\left( {a + b + c} \right)}^2}}}} \right)} \ge 0\]
Vậy có đpcm
$$\boxed{\boxed{I\heartsuit MATHEMATICAL}}$$
![]() Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya
Sức hấp dẫn của toán học mãnh liệt đến nỗi tôi bắt đầu sao nhãng các môn học khác - Sofia Vasilyevna Kovalevskaya ![]()
#4
 Đã gửi 21-04-2017 - 00:58
Đã gửi 21-04-2017 - 00:58

Cho a,b,c là các số thực dương. CMR: $\sum \frac{2a}{b+c}\geq 3+\frac{(a-b)^2+(b-c)^2+(c-a)^2}{(a+b+c)^2}$
Ta có
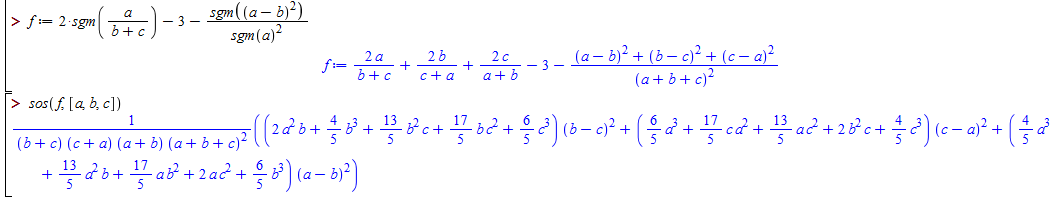
- Dark Magician 2k2 yêu thích
Ho Chi Minh City University Of Transport
#5
 Đã gửi 22-04-2017 - 20:26
Đã gửi 22-04-2017 - 20:26

- quangantoan và Mr Cooper thích
Anh sẽ vẫn bên em dù bất cứ nơi đâu
Anh sẽ là hạt bụi bay theo gió
Anh sẽ là ngôi sao trên bầu trời phương Bắc
Anh không bao giờ dừng lại ở một nơi nào
Anh sẽ là ngọn gió thổi qua các ngọn cây
Em sẽ mãi mãi đợi anh chứ ??
will you wait for me forever
1 người đang xem chủ đề
0 thành viên, 1 khách, 0 thành viên ẩn danh







