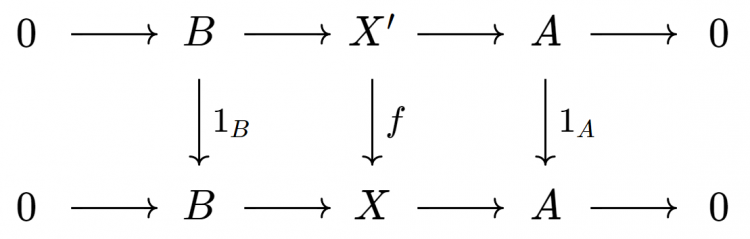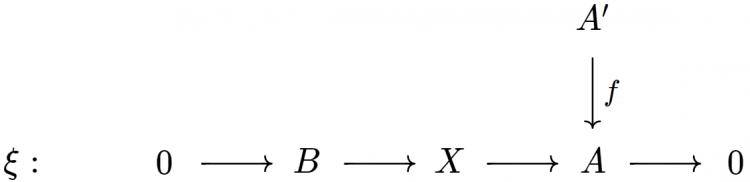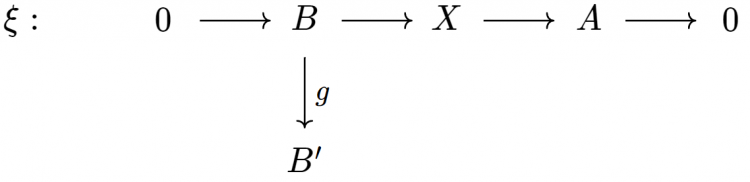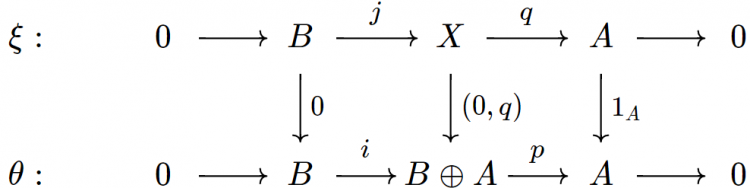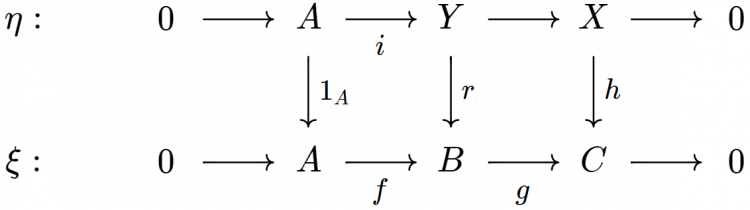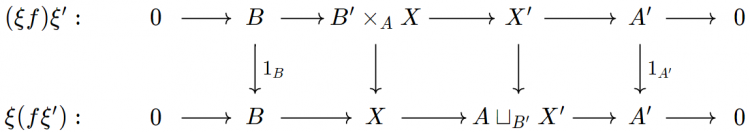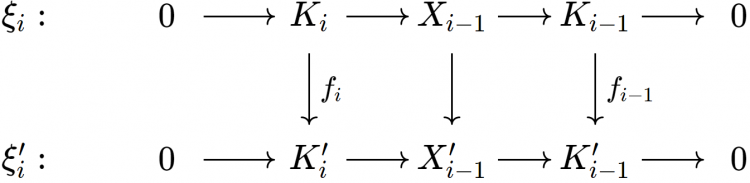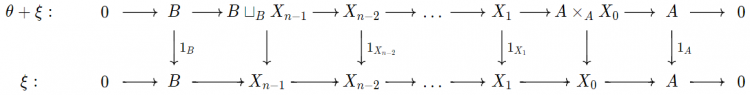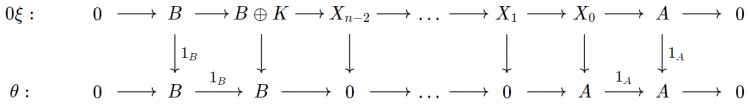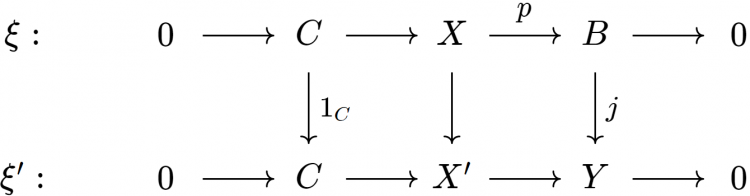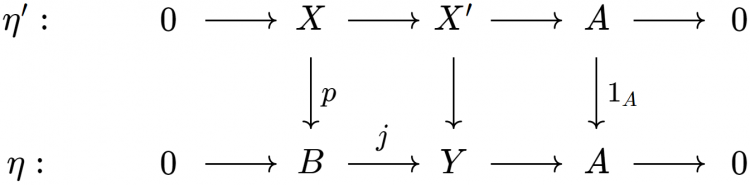Các hàm tử $\text{Hom}$ phản biến và thuận biến của một phạm trù abel là các hàm tử khớp trái. Khi phạm trù đã cho có đủ xạ ảnh hoặc đủ nội xạ, ta có thể xây dựng các hàm tử $\text{Ext}^n$ với tư cách là dẫn xuất phải thứ $n$ của $\text{Hom}$, $n = 1,2,\ldots$. Năm 1934, Baer đã đưa ra mô tả cụ thể cho nhóm $\text{Ext}^1$ bởi các dãy khớp ngắn và phép toán trên đó (tổng Baer). Yoneda đã tổng quát hóa điều này cho các nhóm $\text{Ext}^n$ bởi các mở rộng độ dài $n$ ($n$-fold extensions).
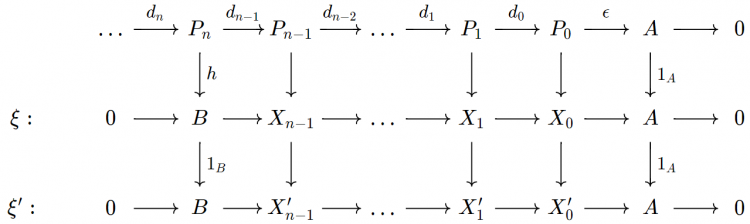
Mục tiêu của các bài viết trong chủ đề này là trình bày lại các xây dựng trên và chỉ ra rằng cách xây dựng cụ thể ở trên của hàm tử $\text{Ext}^n$ trùng với cách xây dựng qua ngôn ngữ hàm tử dẫn xuất. Nội dung được lấy từ chương VII của [Barry Mitchell, Theory of Categories, 1965].
Ta cố định một phạm trù abel $\mathcal{A}$. Khi không có gì nhầm lẫn, ta dùng ký hiệu $\text{Hom}$ thay cho $\text{Hom}_{\mathcal{A}}$ và tương tự với $\text{Ext}^n$. Để tránh "abstract nonsense", ta hoàn toàn có thể làm việc trong một phạm trù cụ thể như phạm trù các mô-đun trên một vành. Khi đó, các chứng minh sẽ đơn giản hơn nhiều vì ta có khái niệm "phần tử".
1. Nhóm $\text{Ext}^1$ và tổng Baer
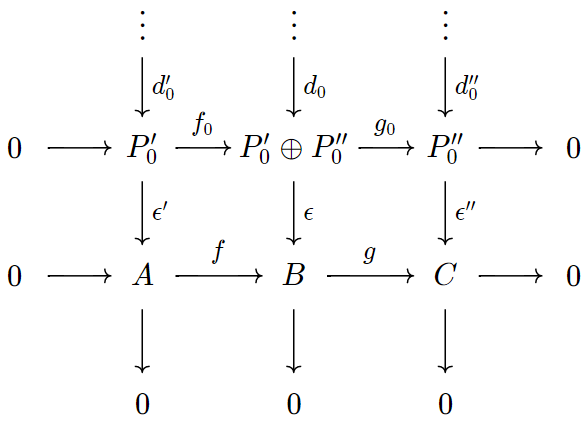
Cho $A$, $B$ là hai vật (của $\mathcal{A}$). Một mở rộng của $A$ bởi $B$ là một dãy khớp ngắn $\xi: 0 \to B \to X \to A \to 0$. Ta nói một mở rộng $\xi': 0 \to B \to X' \to A \to 0$ là tương đương với $\xi$ nếu tồn tại một cấu xạ $f: X' \to X$ sao cho biểu đồ
giao hoán. Theo bổ đề 5, một cấu xạ $f$ như vậy tự động là một đẳng cấu. Lạm dụng ký hiệu, ta sẽ viết $\xi = \xi'$ nếu chúng tương đương. Ta ký hiệu bởi $\text{Ext}^1(A,B)$ lớp tất cả các mở rộng của $A$ bởi $B$ sai khác tương đương (dễ thấy "$=$" là một quan hệ tương đương giữa các mở rộng của $A$ bởi $B$). Có một vấn đề về mặt lý thuyết tập hợp rằng $\text{Ext}^1(A,B)$ có thể quá lớn (tức là một lớp thực sự thay vì là một tập hợp). Tuy nhiên chúng ta sẽ hoàn toàn lờ đi điều này. Dễ thấy nếu $\xi = \xi'$ và $\eta = \eta'$ thì $\xi \oplus \eta = \xi' \oplus \eta'$.
Mục tiêu của chúng ta là định nghĩa một phép toán có tính hàm tử trên $\text{Ext}^1(A,B)$ để nó trở thành một nhóm abel. Ta bắt đầu với tính hàm tử.
Bổ đề 1. Cho $f: A' \to A$ là một cấu xạ. Tồn tại duy nhất (sai khác tương đương) một cách nhúng biểu đồ
vào một biểu đồ giao hoán với hai hàng khớp:
Hàng trên của biểu đồ này là một mở rộng của $A'$ bởi $B$. Ta gọi nó là kéo lùi của $\xi$ bởi $f$ và ký hiệu nó bởi $\xi f$ (ta sẽ sớm thấy lợi thế của ký hiệu này so với ký hiệu $f^\ast \xi$).
Chứng minh
Trước hết, ta chứng minh tính duy nhất. Thật vậy, theo tính chất phổ dụng của tích theo thớ (fibered product) $X \times_A A'$, ta có một cấu xạ $X' \to X \times_A A'$, và ta dễ dàng kiểm tra rằng nó cho ta một tương đương giữa hai mở rộng $0 \to B \to X' \to A' \to 0$ và $0 \to B \to X \times_A A' \to A' \to 0$. Để chứng minh sự tồn tại, ta chỉ cần chỉ ra rằng dãy $0 \to B \to X \times_A A' \to A' \to 0$ khớp. Đây là một bài tập cơ bản của đại số đồng điều: trước hết, vì $X \to A$ là một toàn cấu nên $A$ chính là tổng hỗn tạp (amalgamated sum) của $X$ và $A'$ dọc theo $X \times_A A'$. Chi tiết xem ở The Stacks project 08N4. $\square$
Như vậy, mỗi cấu xạ $f: A' \to A$ cảm sinh một ánh xạ $f^\ast: \text{Ext}^1(A,B) \to \text{Ext}^1(A',B), \quad \xi \mapsto \xi f$.
Một cách đối ngẫu (chẳng hạn, ta có thể làm việc trong $\mathcal{A}^{\text{op}}$), nếu $g: B \to B'$ là một cấu xạ thì tồn tại duy nhất một cách nhúng biểu đồ
vào một biểu đồ giao hoán với hai hàng khớp
Trong trường hợp này, $X'$ là tổng hỗn tạp $X \sqcup_B B'$. Hàng dưới của biểu đồ trên là một mở rộng của $A$ bởi $B'$. Ta gọi nó là đẩy xuôi của $\xi$ bởi $g$ và ký hiệu nó bởi $g \xi$.
Ta có một ánh xạ $g_\ast: \text{Ext}^1(A,B) \to \text{Ext}^1(A,B'), \quad \xi \mapsto g\xi$.
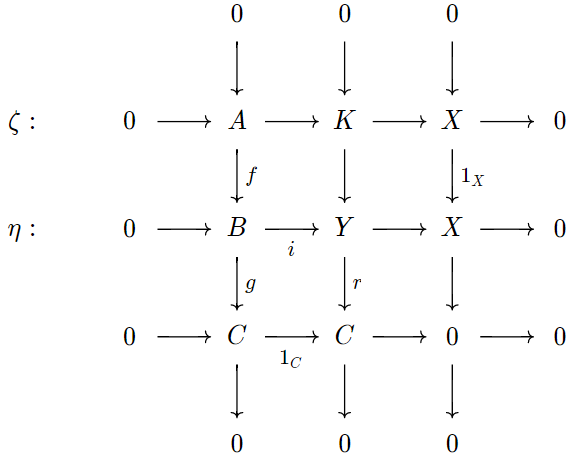
Bổ đề 2. Cho $\xi: 0 \to B \to X \to A \to 0$ và $\xi': 0 \to B' \to X' \to A' \to 0$ là các dãy khớp ngắn. Cho một cấu xạ $\xi' \to \xi$ giữa chúng, và ký hiệu $f: A' \to A$ và $g: B' \to B$ là các cấu xạ tương ứng. Khi đó $\xi' \to \xi$ phân tích qua một mở rộng $\xi''$ của $A'$ bởi $B$ sao cho $\xi'' = g \xi' = \xi f$.
Chứng minh
Ta lấy $\xi'' = \xi f$ rồi xây dựng một cấu xạ $X' \to X \times_A A'$ bằng tính chất phổ dụng của tích theo thớ, từ đó ta có một cấu xạ $\xi' \to \xi''$ với hai đầu là $g: B' \to B$ và $1_{A'}: A' \to A'$. Do tính duy nhất nên ta có $\xi'' = g \xi'$. $\square$
Bổ đề 3. Cho $\xi: 0 \to B \to X \to A \to 0$ là một mở rộng. Cho $f: A' \to A, f': A'' \to A', g: B \to B'$ và $g': B' \to B''$ là các cấu xạ. Ta có các đẳng thức sau
(i) $1_B \xi = \xi 1_A = \xi$.
(ii) $(g'g)\xi = g'(g\xi)$ và $\xi(ff') = (\xi f)f'$.
(iii) $(g \xi) f = g(\xi f)$.
Nói cách khác, các xây dựng $f^\ast$ và $g_\ast$ có tính hàm tử và tương thích với nhau. Nói riêng, ta có một hàm tử hai biến $\text{Ext}^1(-,-): \mathcal{A}^{\text{op}} \times \mathcal{A} \to \mathbf{Sets}.$ Ngoài ra, ta có thể viết $gg' \xi, \xi ff'$ và $g\xi f$ mà không gây bất kỳ nhầm lẫn nào.
Chứng minh
(i) và (ii) là hiển nhiên. Để chứng minh (iii), ta xét các cấu xạ tự nhiên $\xi f \to \xi$ và $\xi \to g\xi$. Áp dụng Bổ đề 2, ta có thể phân tích hợp thành $\xi f \to g\xi$ qua một mở rộng $\xi'$ của $A'$ bởi $B'$ sao cho $\xi' = g(\xi f) = (g \xi)f$. $\square$
Khi $A$ là một vật, ta ký hiệu $\Delta: A \to A \oplus A$ là cấu xạ đường chéo, $\nabla: A \oplus A \to A$ là cấu xạ "cộng", và $\tau: A \oplus A \to A \oplus A$ là cấu xạ "đổi chỗ hai tọa độ".
Cho $A$ và $B$ là hai vật. Ta định nghĩa phép toán $+$ (được gọi là tổng Baer) trên tập hợp $\text{Ext}^1(A,B)$ bởi $$\xi+\xi':=\nabla (\xi \oplus \xi') \Delta$$ (tất nhiên, để vế phải có nghĩa thì $\nabla: B \oplus B \to B$ và $\Delta: A \to A \oplus A$). Cụ thể, nếu $\xi: 0 \to B \xrightarrow{i} X \to A \to 0$ và $\xi': 0 \to B \xrightarrow{i'} X' \to A \to 0$ thì $\xi + \xi'$ là mở rộng $$0 \to B \to \text{Coker}(B \xrightarrow{(i,-i')} X \times_A X') \to A \to 0.$$
Bổ đề 4. Các đẳng thức sau là đúng một khi một trong hai vế có nghĩa.
(i) $(g \oplus g')(\xi \oplus \xi') = g\xi \oplus g'\xi'$ và $(\xi \oplus \xi')(f \oplus f') = \xi f \oplus \xi' f'$.
(ii) $\xi \nabla = \nabla(\xi \oplus \xi)$ và $\Delta \xi = (\xi \oplus \xi) \Delta$.
(iii) $(g + g')\xi = g\xi + g'\xi$ và $\xi (f + f') = \xi f + \xi f'$.
(iv) $g(\xi + \xi') = g\xi + g\xi'$ và $(\xi + \xi')f = \xi f + \xi' f$.
Chứng minh
(i) suy ra là tính hàm tử của song tích $\oplus$. (ii) được suy ra từ Bổ đề 2 áp dụng cho cấu xạ cộng $\xi \oplus \xi \to \xi$ cũng như cấu xạ đường chéo $\xi \to \xi \oplus \xi$. Để chứng minh (iii), ta nhận xét rằng $g + g' = \nabla(g \oplus g') \Delta$, vì thế $$(g+g')\xi = \nabla(g \oplus g') \Delta \xi = \nabla(g \oplus g') (\xi \oplus \xi) \Delta = \nabla(g \xi \oplus g'\xi) \Delta = g\xi + g'\xi,$$ và tương tự cho đẳng thức $\xi (f + f') = \xi f + \xi f'$. Để chứng minh (iv), chú ý rằng $g \nabla = \nabla(g \oplus g)$, do đó $$g(\xi + \xi') = g\nabla(\xi \oplus \xi') \Delta = \nabla(g \oplus g)(\xi \oplus \xi') \Delta = \nabla(g \xi \oplus g\xi') \Delta = g\xi + g\xi',$$ và tương tự cho đẳng thức $(\xi + \xi')f = \xi f + \xi' f$. $\square$
Định lý 5. Cho $A$ và $B$ là các vật. Tập hợp $\text{Ext}^1(A,B)$ cùng với tổng Baer là một nhóm abel.
Chứng minh
Tính kết hợp. Cho $\xi,\xi'$ và $\xi''$ là các mở rộng của $A$ bởi $B$. Ta có $$(\xi + \xi') + \xi'' = \nabla(\xi \oplus \xi') \Delta + \xi'' = \nabla((\nabla(\xi \oplus \xi') \Delta) \oplus \xi'')\Delta = \nabla(\nabla \oplus 1_B)(\xi \oplus \xi' \oplus \xi'')(\Delta \oplus 1_A)\Delta.$$ Sử dụng các đẳng thức $\nabla(\nabla \oplus 1_B) = \nabla(1_B \oplus \nabla)$ và $(\Delta \oplus 1_A)\Delta = (1_A \oplus \Delta) \Delta$, ta thu được $$(\xi + \xi') + \xi'' = \nabla(1_B \oplus \nabla)(\xi \oplus \xi' \oplus \xi'')(1_A \oplus \Delta)\Delta = \nabla(\xi \oplus (\nabla(\xi' \oplus \xi'')\Delta))\Delta = \xi + (\xi' + \xi'').$$
Tính giao hoán. Cho $\xi$ và $\xi'$ là các mở rộng của $A$ bởi $B$. Các cấu xạ đổi chỗ hai tọa độ cảm sinh một cấu xạ hiển nhiên $\xi \oplus \xi' \to \xi' \oplus \xi$. Theo Bổ đề 2, ta có $\tau(\xi \oplus \xi') = (\xi' \oplus \xi) \tau$. Hiển nhiên, ta có $\nabla \tau = \nabla$ và $\tau \Delta = \Delta$, do đó $$\xi + \xi' = \nabla(\xi \oplus \xi') \Delta = \nabla \tau(\xi \oplus \xi') \Delta = \nabla(\xi' \oplus \xi) \tau \Delta = \nabla(\xi' \oplus \xi) \Delta = \xi' + \xi.$$
Phần tử trung lập. Ta chỉ rằng rằng dãy khớp chẻ $\theta: 0 \to B \xrightarrow{i} B \oplus A \xrightarrow{p} A \to 0$ là phần tử trung lập của tổng Baer. Thật vậy, nếu $\xi: 0 \to B \xrightarrow{j} X \xrightarrow{q} A \to 0$ là một mở rộng của $A$ bởi $B$, ta có biểu đồ giao hoán với các dòng khớp:
trong đó $\alpha$ là hợp thành của $q$ và phép chiếu lên tọa độ thứ hai $B \oplus X \to X$. Từ đó ta thấy rằng hàng giữa của biểu đồ trên là $(\theta \oplus \xi) \Delta$ và vì thế hàng dưới bằng $$\xi = \nabla(\theta \oplus \xi) \Delta = \theta + \xi.$$
Phần tử đối. Xét $\theta$ và $\xi$ như trên. Ta có biểu đồ giao hoán với hai hàng khớp
Từ đó ta có $0 \xi = \theta$. Do đó $$\xi + (-1_B)\xi = (1_B + (-1_B))\xi = 0\xi = \theta,$$ nghĩa là $(-1_B)\xi$ là một phần tử đối của $\xi$. $\square$
Như vậy, $\text{Ext}^1(A,B)$ là một nhóm abel với mọi vật $A$ và $B$. Nếu $f: A' \to A$ và $g: B \to B'$ là các cấu xạ thì các ánh xạ cảm sinh $f^\ast: \text{Ext}^1(A,B) \to \text{Ext}^1(A',B)$ và $g_\ast: \text{Ext}^1(A,B) \to \text{Ext}^1(A,B')$ là các đồng cấu nhóm theo Bổ đề 4. Như vậy, ta đã xây dựng hàm tử hai biến $\text{Ext}^1(-,-): \mathcal{A}^{\text{op}} \times \mathcal{A} \to \mathbf{Ab}.$
File gửi kèm
Bài viết đã được chỉnh sửa nội dung bởi nmlinh16: 07-05-2021 - 14:03