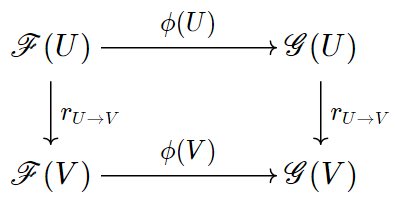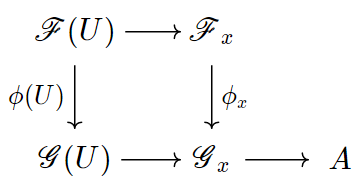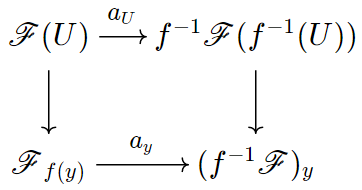Chủ đề này có 7 trả lời

[nmlinh16]

Khái niệm bó (sheaf) thể hiện một ý tưởng cơ bản: để hiểu một không gian hình học, ta có thể nghiên cứu các hàm trên không gian đó. Bó vốn có nguồn gốc từ Tô pô đại số và hình học vi phân (Leray đã xây dựng nó để chứng minh các định lý điểm bất động trong PDE). Sau này, người ta sử dụng bó một cách có hệ thống trong hình học đại số hiện đại.

 

1. "Hàm" và "điểm"

 

Trước khi đến với nội dung chính, ta bắt đầu một phiên bản baby của định lý biểu diễn Gelfand-Naimark.

 

Nếu $A$ là một vành (giao hoán và có đơn vị), ta ký hiệu $\text{Spm}(A)$ là phổ cực đại của $A$, tức là tập hợp tất cả các ideal cực đại của $A$. Trên tập hợp này có một tô-pô được gọi là tô-pô Zariski, trong đó các tập đóng là các tập hợp $$V(I):=\{\mathfrak{m} \in \text{Spm}(A): I \subseteq \mathfrak{m}\},$$ trong đó $I$ là một ideal nào đó của $A$. Thật vậy, $\varnothing = V((1))$, $\text{Spm}(A) = V((0))$, $V(I) \cup V(J) = V(IJ)$ và $\bigcap_i V(I_i) = V\left(\sum_i I_i\right)$. Tô-pô này sinh bởi các tập mở có dạng $$D(f):=\{\mathfrak{m} \in \text{Spm}(A): f \notin \mathfrak{m}\},$$ với $f \in A$, được gọi là các tập mở chính. Như vậy, ta có thể coi các phần tử của $A$ như các hàm trên không gian tô-pô $\text{Spm}(A)$. Các ideal cực đại của $A$ chính là các điểm. Việc tính giá trị của một hàm $f$ tại một điểm $\mathfrak{m}$ chính là việc tính $f \mod \mathfrak{m}$, đó là một phần tử của trường thặng dư $A / \mathfrak{m}$. Như vậy, hàm $f$ nhận giá trị trong một trường biến thiên theo từng điểm. 

Slogan: Trong hình học, điểm là một cái gì đó mà tại đó ta có thể tính giá trị của các hàm, các giá trị này nằm trong một trường nào đó.

 

 

Cho $X$ là một không gian tô-pô. Ký hiệu $\mathcal{C}(X)$ là vành các hàm liên tục $X \to \mathbb{R}$ (phép cộng và phép nhân được định nghĩa một cách hiển nhiên). Nhóm các phần tử khả nghịch của vành này là $$\mathcal{C}(X)^\ast = \{f \in \mathcal{C}(X): \forall x \in X, f(x) \neq 0\}.$$ Với mỗi điểm $x \in X$, tập hợp $\mathfrak{m}_x:=\{f \in \mathcal{C}(X): f(x) = 0\}$ là một ideal của $\mathcal{C}(X)$. Chính xác thì nó là hạch của toàn cấu $$\mathcal{C}(X) \to \mathbb{R}, \qquad f \mapsto f(x).$$ Nó là một ideal cực đại vì $\mathcal{C}(X)/\mathfrak{m}_x \simeq \mathbb{R}$ là một trường. Ta có một ánh xạ $$X \to \text{Spm}(\mathcal{C}(X)), \qquad x \mapsto m_x.$$

 

Mệnh đề. Nếu $X$ là Hausdorff và compact thì ánh xạ trên là một phép đồng phôi (trong đó tô-pô trên $\text{Spm}(\mathcal{C}(X))$ là tô-pô Zariski).

Chứng minh

Tính toàn ánh. Cho $\mathfrak{m}$ là một ideal cực đại của $\mathcal{C}(X)$. Ta chứng minh rằng tồn tại $x \in X$ sao cho $\mathfrak{m} \subseteq \mathfrak{m}_x$ (và vì thế $\mathfrak{m} = \mathfrak{m}_x$ vì chúng là các ideal cực đại). Thật vậy, nếu ngược lại thì với mọi $x \in X$, tồn tại $f_x \in \mathfrak{m}$ sao cho $f_x(x) \neq 0$. Lấy $U_x \subseteq X$ là một lân cận mở của $x$ sao cho $f_x$ nhận giá trị khác $0$ trên toàn $U_x$. Vì $X$ là compact nên tồn tại một tập con hữu hạn $S \subseteq X$ sao cho $X = \bigcup_{x \in S}U_x$. Đặt $f:=\sum_{x \in S} f_x^2 \in \mathfrak{m}$. Thế thì $f(y) > 0$ với mọi $y \in X$, do đó $f$ khả nghịch trong $\mathcal{C}(X)^\times$, suy ra $\mathfrak{m} = \mathcal{C}(X)$, mâu thuẫn.

Tính đơn ánh. Cho $x \neq y$ là hai điểm của $X$. Vì $X$ là Hausdorff và compact nên chuẩn tắc. Theo định lý Urysohn, tồn tại hàm liên tục $f: X \to \mathbb{R}$ sao cho $f(x) = 0$ và $f(y) \neq 0$, suy ra $\mathfrak{m}_x \neq \mathfrak{m}_y$.

Tính liên tục. Xét một tập mở chính $D(f)$ của $\text{Spm}(\mathcal{C}(X))$, với $f: X \to \mathbb{R}$ liên tục. Ảnh ngược của nó bởi ánh xạ $$X \to \text{Spm}(\mathcal{C}(X)), \qquad x \mapsto \mathfrak{m}_x$$ là $\{x \in X: f(x) \neq 0\}$, hiển nhiên đây là một tập mở. Các tập mở chính là một cơ sở cho tô-pô Zariski trên $\text{Spm}(\mathcal{C}(X))$ nên ánh xạ trên liên tục.

Tính đóng. Cho $Y$ là một tập con đóng của $X$. Ta sẽ chứng minh rằng $$\{\mathfrak{m}_x: x \in Y\} = V(I),$$ với $I = \bigcap_{x \in Y} \mathfrak{m}_x = \{f \in \mathcal{C}(X): f|_Y = 0\}$. Hiển nhiên ta có $\{\mathfrak{m}_x: x \in Y\} \subseteq V(I)$. Ngược lại, xét $\mathfrak{m} \in V(I)$. Ta có $\mathfrak{m} = \mathfrak{m}_x$ với $x \in X$ nào đó. Nếu $x \notin Y$ thì tồn tại $f: X \to \mathbb{R}$ liên tục sao cho $f(x) \neq 0$ và $f|_Y = 0$ (vì $X$ là chuẩn tắc, nói riêng là chính quy). Khi đó, $f \in I$ và $f \notin \mathfrak{m}_x$. Nhưng $\mathfrak{m}_x \in V(I)$ nên $I \subseteq \mathfrak{m}_x$. Tóm lại, $x \in Y$ và do đó ta có $\{\mathfrak{m}_x: x \in Y\} = V(I)$ là một tập đóng. $\square$

[nmlinh16]

2. Tiền bó

 

Cho $X$ là một không gian tô-pô. Như ở bài trước, ta đã thấy rằng nếu $X$ là Hausdorff và compact thì ta có thể nghiên cứu $X$ thông qua vành các hàm liên tục $X \to \mathbb{R}$ (mà không bị mất thông tin). Tuy nhiên, việc chỉ xét các hàm trên toàn bộ $X$ nói chung là không đủ (chẳng hạn, trong hình học đại số, các không gian tô-pô mà chúng ta xét là các lược đồ (scheme), chúng hầu như không bao giờ là Hausdorff). Từ đó người ta nghĩ đến việc xét các hàm xác định trên một tập mở của $X$, đó là cơ sở của khái niệm bó.

 

Để gọn gàng, mình sẽ trình bày các định nghĩa bằng ngôn ngữ phạm trù và hàm tử, nhưng mình cũng sẽ giải thích các định nghĩa sao cho người đọc chưa biết đến ngôn ngữ này cũng có thể hiểu.

 

Ký hiệu bởi $O(X)$ phạm trù các tập mở của $X$, trong đó các cấu xạ là các phép bao hàm (như vậy, nếu $U, V \subseteq X$ là các tập mở thì có duy nhất một cấu xạ $U \to V$ nếu $U \subseteq V$, và không có cấu xạ $U \to V$ nào nếu ngược lại).

Một tiền bó (presheaf) nhóm abel trên $X$ là một hàm tử phản biến từ $O(X)$ vào phạm trù các nhóm abel. Một cách cụ thể, một tiền bó $\mathscr{F}$ trên $X$ được cho bởi các dữ liệu sau đây

1. với mỗi tập mở $U$ của $X$, một nhóm abel $\mathscr{F}(U)$;
2. với $V \subseteq U$ là các tập mở của $X$, một đồng cấu nhóm $r_{U \to V}: \mathscr{F}(U) \to \mathscr{F}(V)$, thường được gọi là phép hạn chế từ $U$ vào $V$.

sao cho các tính chất sau đây được thỏa mãn

1. với mọi tập mở $U \subseteq X$, $r_{U \to U}: \mathscr{F}(U) \to \mathscr{F}(U)$ là cấu xạ đồng nhất;
2. với $W \subseteq V \subseteq U$ là các tập mở của $X$, ta có $r_{V \to W} \circ r_{U \to V} = r_{U \to W}: \mathscr{F}(U) \to \mathscr{F}(W)$.

Tương tự, ta có thể nói về tiền bó tập hợp, tiền bó vành, tiền bó module...

 

Ví dụ. 

1. Ta có (tiền) bó $\mathcal{C}^0$ các hàm liên tục trên $X$ cho bởi $U \mapsto \mathcal{C}^0(U,\mathbb{R})$, trong đó $\mathcal{C}^0(U,\mathbb{R})$ là vành các hàm liên tục $U \to \mathbb{R}$. Các phép hạn chế được hiểu theo nghĩa thông thường.
2. Tương tự, cho $X$ là một đa tạp trơn. Ta có (tiền) bó $\mathcal{C}^\infty$ các hàm khả vi trên $X$ cho bởi $U \mapsto \mathcal{C}^\infty(U, \mathbb{R})$.
3. Tương tự, cho $X$ là một đa tạp giải tích phức (chẳng hạn, một diện Riemann). Ta có (tiền) bó $\mathcal{O}$ các hàm chỉnh hình) $U \mapsto \mathcal{O}(U,\mathbb{C})$.
4. Cho $A$ là một nhóm abel. Tiền bó hằng $\underline{A}^{\text{pre}}$ trên $X$ được cho bởi $U \mapsto A$. Các phép hạn chế là các cấu xạ đồng nhất $A \to A$.
5. Cho $x \in X$ và $A$ là một nhóm abel. (Tiền) bó chọc trời $i_{x,\ast} A$ trên $X$ được cho bởi $U \mapsto \begin{cases} A & \text{nếu } x \in U, \\ 0 & \text{nếu } x \notin U.\end{cases}$. Các phép hạn chế đều hiển nhiên (cấu xạ đồng nhất $A \to A$, hoặc $A \to 0$, hoặc $0 \to 0$).
6. Cho $A$ là một vành (giao hoán, có đơn vị). Không gian tô-pô $X = \text{Spec}(A)$ được định nghĩa là tập hợp các ideal nguyên tố của $A$ cùng với tô-pô Zariski (tương tự như $\text{Spm}(A)$), đó là phổ (nguyên tố) của $A$. Có duy nhất một bó (sẽ định nghĩa bó ở bài sau) vành $\mathcal{O}_X$ trên $X$ sao cho trên mỗi tập mở chính $D(f) = \{\mathfrak{p} \in \text{Spec}(A): f \notin \mathfrak{p}\}$, $f \in A$, ta có $\mathcal{O}_X(D(f)) = A_f$, địa phương hóa của $A$ tại tập con nhân tính $\{1,f,f^2,\ldots\}$. Các phép hạn chế giữa các tập mở chính là các cấu xạ địa phương hóa. Bó $\mathcal{O}_X$ được gọi là bó cấu trúc của $X$. Đây là viên gạch cơ bản trong hình học đại số: cặp $(X, \mathcal{O}_X)$ được gọi là một lược đồ affine. Một lược đồ được xây dựng bằng cách "dán" các lược đồ affine.

Cho $\mathscr{F}$ là một tiền bó (nhóm abel) trên $X$. Với mỗi tập mở $U$, ta cũng dùng các ký hiệu $\Gamma(U, \mathscr{F})$ và $\mathrm{H}^0(U, \mathscr{F})$ để chỉ nhóm $\mathcal{F}(U)$. Các phần tử của nhóm này được gọi là các lớp cắt (section) của $\mathscr{F}$ trên $U$. Nếu $V \subseteq U$ là một tập mở và $s \in \Gamma(U,\mathscr{F})$ là một lớp cắt, ta cũng dùng ký hiệu $s|_V$ để chỉ hạn chế $r_{U \to V}(s)$. Một lớp cắt trên $X$ đưuọc gọi là một lớp cắt toàn cục (global section).

 

Cho $\mathscr{F}$ và $\mathscr{G}$ là các tiền bó trên $X$. Theo định nghĩa, chúng là các hàm tử phản biến từ phạm trù các tập mở của $X$ vào phạm trù các nhóm abel. Một cấu xạ $\phi: \mathscr{F} \to \mathscr{G}$ là một biến đổi tự nhiên giữa hai hàm tử này. Một cách cụ thể, nó được cho bởi một họ các đồng cấu nhóm $\phi(U): \mathscr{F}(U) \to \mathscr{G}(U)$ các đồng cấu nhóm, được đánh số bởi các tập mở $U$ của $X$, sao cho nếu $V \subseteq U$ là các tập mở của $X$ thì ta có biểu đồ giao hoán

Nếu $U$ là một tập mở của $X$ và $s$ là một lớp cắt của $\mathscr{F}$ trên $U$, ta ký hiệu $\phi(s)$ thay cho $\phi(U)(s)$. Đó là một lớp cắt của $\mathscr{G}$ trên $U$. Tính giao hoán của biểu đồ trên có thể viết lại thành $\phi(s|_V) = \phi(s)|_V$ với mọi $s \in \Gamma(U,\mathscr{F})$. Các tiền bó trên $X$ cùng các cấu xạ giữa chúng tạo thành một phạm trù mà ta ký hiệu bởi $\mathbf{PSh}(X)$. Đây là một phạm trù tiền cộng tính: nếu $\phi, \psi: \mathscr{F} \to \mathscr{G}$ là các cấu xạ giữa hai tiền bó trên $X$, cấu xạ $\phi + \psi: \mathscr{F} \to \mathscr{G}$ được định nghĩa một cách hiển nhiên, $$(\phi + \psi)(U):=\phi(U) + \psi(U).$$

 

Một cách thủ tục, ta kiểm tra được rằng $\mathbf{PSh}(X)$ là một phạm trù abel. Tổng trực tiếp của hai tiền bó $\mathscr{F}$ và $\mathscr{G}$ là tiền bó $$\mathscr{F} \oplus \mathscr{G}: U \mapsto \mathscr{F}(U) \oplus \mathscr{G}(U).$$ Nếu $\phi: \mathscr{F} \to \mathscr{G}$ là một đồng cấu giữa hai tiền bó thì hạch (tương ứng, đối hạch; tương ứng, ảnh) của $\phi$ là tiền bó $\text{Ker} \phi: U \mapsto \text{Ker} (\phi (U))$ (tương ứng, $\text{Coker} \phi: U \mapsto \text{Coker}(\phi(U))$; tương ứng, $\text{Im} \phi: U \mapsto \text{Im}(\phi(U))$). Cấu xạ $\phi$ là một đơn cấu (tương ứng, toàn cấu; tương ứng, đẳng cấu) trong phạm trù $\mathbf{PSh}(X)$khi và chỉ khi $\phi(U)$ là một đơn cấu (tương ứng, toàn cấu; tương ứng, đẳng cấu) với mọi tập mở $U \subseteq X$. Nói riêng, nếu $\mathscr{F} (U) \subseteq \mathscr{G}(U)$ với mọi tập mở $U \subseteq X$ thì ta gọi $\mathcal{F}$ là một tiền bó con của $\mathscr{G}$ và tiền bó thương $\mathscr{G} / \mathscr{F}$ được cho bởi $U \mapsto \mathscr{G}(U) / \mathscr{F}(U)$.

 

File gửi kèm

•  1.png   8.35K   56 Số lần tải

[nmlinh16]

3. Thớ và bó

 

Ta vẫn cho $X$ là một không gian tô-pô.

 

Cho $\mathscr{F}$ là một tiền bó trên $X$. Cho $x \in X$. Thớ (stalk) của $\mathscr{F}$ tại $x$ là giới hạn xuôi $$\mathscr{F}_x:= \varinjlim_{U \owns x} \mathscr{F}(U).$$ Cụ thể, ta có các đồng cấu chính tắc $\mathcal{F}(U) \to \mathscr{F}_x$ với mỗi lân cận mở $U$ của $x$. Ảnh của mỗi lớp cắt $s \in \Gamma(U, \mathscr{F})$ bởi đồng cấu này được ký hiệu bởi $s_x \in \mathscr{F}_x$, và được gọi là mầm (germ) của $s$ tại $x$. Mỗi phần tử của $\mathscr{F}_x$ đều là mầm của một lớp cắt nào đó xác định trong lân cận của $x$. Nếu $U, V$ là các lân cận mở của $x$ và $s \in  \Gamma(U, \mathscr{F})$, $t \in \Gamma(V, \mathscr{F})$ thì $s_x = t_x$ khi và chỉ khi tồn tại lân cận mở $W \subseteq U \cap V$ của $x$ sao cho $s|_W = t|_W$.

 

Ví dụ.

1. Xét tiền bó $\mathcal{O}$ các hàm chỉnh hình trên $\mathbb{C}$ (Đây là một tiền bó $\mathbb{C}$-đại số). Với mỗi $a \in \mathbb{C}$, thớ $\mathcal{O}_a$ đẳng cấu với vành $\mathbb{C}\{z - a\}$ các chuỗi lũy thừa với tâm tại $a$ và bán kính hội tụ dương. 
2. Cho $A$ là một nhóm abel. Tiền bó hằng $\underline{A}^{\text{pre}}: U \mapsto A$ trên $X$ có thớ bằng $A$ tại mọi điểm.
3. Cho $A$ là một nhóm abel và $x \in X$. Tiền bó chọc trời $i_{x,\ast} A$ có thớ $A$ tại mọi điểm $y \in \overline{\{x\}}$ (các điểm đặc biệt hóa của $x$) và $0$ tại các điểm khác.
4. Cho $A$ là một vành (giao hoán, có đơn vị) và $X = \text{Spec}(A)$, với mỗi ideal nguyên tố $\mathfrak{p} \in X$, thớ $\mathcal{O}_{X,\mathfrak{p}}$ của bó cấu trúc $\mathcal{O}_X$ là địa phương hóa $A_{\mathfrak{p}}$ của $A$ tại $\mathfrak{p}$.

 

Một tiền bó $\mathcal{F}$ trên $X$ được gọi là một bó nếu nó thỏa mãn hai điều kiện sau đây với mọi tập mở $U$ của $X$ và mọi phủ mở $U = \bigcup_{i \in I} U_i$.

1. (Tính địa phương) Nếu $s \in \mathscr{F}(U)$ sao cho $s|_{U_i} = 0$ với mọi $i \in I$ thì $s = 0$.
2. (Tính dán được) Nếu $s_i \in \mathscr{F}(U_i)$ với mỗi $i \in I$ sao cho $s_i|_{U_i \cap U_j} = s_j|_{U_i \cap U_j}$ với mọi $i, j \in I$ thì tồn tại $s \in \mathcal{F}(U)$ sao cho $s|_{U_i} = s_i$ với mọi $i \in I$ (lớp cắt $s$ này là duy nhất do tính địa phương).

Nhận xét.

1. Từ tính địa phương, ta suy ra rằng với mọi tập mở $U$ thì $\mathscr{F}(U) \to \prod_{x \in U} \mathscr{F}_x$ là một đơn cấu (nói riêng, nếu $\mathscr{F}_x 0 $ với mọi $x \in U$ thì $\mathscr{F}(U) = 0$). Thật vậy, giả sử $s \in \mathscr{F}(U)$ sao cho $s_x = 0$ với mọi $x \in U$. Tồn tại lân cận mở $U_x \subseteq U$ của $x$ sao cho $s|_{U_x} = 0$. Vì các tập mở $U_x$ phủ $U$ nên ta có $s = 0$.
2. Áp dụng tính dán được duy nhất cho $U = \varnothing$, ta thấy $\mathscr{F}(\varnothing) = 0$.

Phạm trù $\mathbf{Sh}(X)$ các bó trên $X$ được định nghĩa là phạm trù con đầy của phạm trù con đầy của phạm trù $\mathbf{Psh}(X)$ các tiền bó. Nói cách khác, một đồng cấu giữa hai bó đơn giản là một đồng cấu giữa hai tiền bó tương ứng.

 

 

Ví dụ.

1. Tiền bó các hàm liên tục, tiền bó các hàm khả vi và tiền bó các hàm chỉnh hình đều là các bó.
2. Tiền bó chọc trời là một bó.
3. Nếu $A$ là một vành giao hoán có đơn vị và $X = \text{Spec}(A)$ thì tiền bó cấu trúc $\mathcal{O}_X$ là một bó.
4. Cho $X = \{0,1\}$ với tô-pô rời rạc và $A$ là một abel khác $0$. Tiền bó $\underline{A}^{\text{pre}}$  trên $A$ không phải là một bó. 
5. Bó hằng $\underline{A}$ trên không gian tô-pô $X$ được cho bởi $U \mapsto \{\text{hàm hằng địa phương } U \to A\}$.

 

Việc lấy thớ có tính hàm tử. Cho $\phi: \mathscr{F} \to \mathscr{G}$ là một cấu xạ giữa hai tiền bó trên $X$. Cho $x \in X$. Lấy giới hạn, ta có một cấu xạ $\phi_x: \mathscr{F}_x \to \mathscr{G}_x$ được mô tả như sau. Nếu $U$ là một lân cận mở của $x$ và $s \in \mathscr{F}(U)$ thì $\phi_x(s_x) = \phi(s)_x$.

 

Sau đây là các tính chất của bó có thể kiểm tra trên thớ.

 

Mệnh đề. Cho $\phi: \mathscr{F} \to \mathscr{G}$ là một cấu xạ giữa hai bó trên $X$. 

1. Nếu $\phi_x = 0$ với mọi $x \in X$ thì $\phi = 0$.
2. $\phi$ là một đơn cấu (theo nghĩa tiền bó) khi và chỉ khi $\phi_x$ là một đơn cấu với mọi $x \in X$.
3. $\phi$ là một đẳng cấu (theo nghĩa tiền bó) khi và chỉ khi $\phi_x$ là một đẳng cấu với mọi $x \in X$.

Chú ý rằng tính toàn cấu (theo nghĩa tiền bó) nói chung không kiểm tra được trên thớ.

Chứng minh

1. Giả sử $\phi_x = 0$ với mọi $x \in X$. Cho $U$ là một tập mở của $X$, ta cần chứng minh rằng $\phi(U) = 0: \mathscr{F}(U) \to \mathscr{G}(U)$. Thật vậy, cho $s \in \mathscr{F}(U)$. Khi đó $\phi(s)_x = \phi_x(s_x) = 0$ với mọi $x \in U$. Mà $\mathscr{G}$ là một bó nên $\mathscr{G}(U) \to \prod_{x \in U} \mathscr{G}_x$ là một đơn cấu, suy ra $\phi(s) = 0$.

2. Giả sử $\phi$ là một đơn cấu. Cố định $x \in X$. Lấy $\alpha \in \mathscr{F}_x$ sao cho $\phi_x(\alpha) = 0$. Ta có thể viết $\alpha = s_x$ với $s \in \mathcal{F}(U)$ nào đó và $U$ là một lân cận mở của $x$. Thế thì $\phi(s)_x = \phi_x(s_x) = \phi_x(\alpha) = 0$, nên tồn tại lân cận mở $V \subseteq U$ của $x$ sao cho $\phi(s|_V) = \phi(s)|_V = 0$. Vì $\phi(V)$ là một đơn cấu nên $s|_V = 0$, suy ra $s_x = 0$.

Ngược lại, giả sử $\phi_x$ là một đơn cấu với mọi $x \in X$. Cho $U$ là một tập mở tùy ý của $X$, ta chứng minh rằng $\phi(U): \mathscr{F}(U) \to \mathscr{G}(U)$ là một đơn cấu. Thật vậy, xét $s \in \mathscr{F}(U)$ sao cho $\phi(s) = 0$. Thế thì $\phi_x(s_x) = \phi(s)_x = 0$ với mọi $x \in U$, suy ra $s_x = 0$ vì $x$ là một đơn cấu. Vì $\mathscr{F}$ là một bó nên $s = 0$.

3. Giả sử $\phi$ là một đẳng cấu. Ta chỉ cần chứng minh $\phi_x$ là một toàn cấu với mọi $x \in X$. Thật vậy, xét $\beta \in \mathscr{G}_x$. Ta có thể viết $\beta = t_x$ với $t \in \mathscr{G}(U)$ nào đó và $U$ là một lân cận mở của $x$. Vì $\phi(U)$ là một toàn cấu nên tồn tại $s \in \mathscr{F}(U)$ sao cho $t = \phi(s)$, suy ra $\beta = t_x = \phi(s)_x = \phi_x(s_x)$.

Ngược lại, giả sử $\phi_x$ là một đẳng cấu với mọi $x \in X$. Ta chỉ cần chứng minh $\phi$ là một toàn cấu. Cho $U$ là một tập mở tùy ý của $X$ và $t \in \mathscr{G}(U)$. Ta cần tìm $s \in \mathscr{F}(U)$ sao cho $t = \phi(s)$. Ta sẽ thấy rằng chỉ tính toàn cấu của $\phi_x$ là chưa đủ.

Với mỗi $x \in U$, tồn tại $\alpha_x \in \mathscr{F}_x$ sao cho $\phi_x(\alpha_x) = t_x$. Viết $\alpha_x = r^x_x$, với $r^x \in \mathscr{F}(V_x)$ nào đó và $V_x \subseteq U$ là một lân cận mở của $x$. Thế thì $t_x = \phi_x(\alpha_x) = \phi_x(r^x_x) = \phi(r^x)_x$, nghĩa là tồn tại lân cận mở $U_x \subseteq U$ sao cho $\phi(r^x)|_{U_x} = t|_{U_x}$. Ta thu được phủ mở $U = \bigcup_{x \in U} U_x$ của $U$. Đặt $s^x: = r^x|_{U_x} \in \mathscr{F}(U_x)$. Với $x,y \in U$, ta có $$\phi(s^x|_{U_x \cap U_y}) = \phi(s^x)|_{U_x \cap U_y} = \phi(r^x)|_{U_x \cap U_y} = t|_{U_x \cap U_y}.$$

Tương tự, $$\phi(s^y|_{U_x \cap U_y}) = t|_{U_x \cap U_y}.$$ Vì $\phi(U_x \cap U_y)$ là một đơn cấu (theo phần 2.) nên $s^x|_{U_x \cap U_y} = s^y|_{U_x \cap U_y}$. Vì $\mathscr{F}$ là một bó nên ta có thể dán các lớp cắt $s^x$ thành một lớp cắt $s \in \mathscr{F}(U)$. Với mỗi $x \in U$, ta có $t|_{U_x} = \phi^(r^x)|_{U_x} = \phi(s^x) = \phi(s|_{U_x}) = \phi(s)|_{U_x}$. Vì $\mathscr{G}$ là một bó nên $t = \phi(s)$. $\square$

Bài viết đã được chỉnh sửa nội dung bởi nmlinh16: 24-05-2021 - 22:30

[nmlinh16]

4. Bó hóa

 

Cho $X$ là một không gian tô-pô

Ta dễ dàng kiểm tra được rằng, nếu $\mathscr{F}$ và $\mathscr{G}$ là các bó trên $X$ thì tiền bó tổng trực tiếp $$\mathscr{F} \oplus \mathscr{G}: U \mapsto \mathscr{F}(U) \oplus \mathscr{G}(U)$$ là một bó. Tương tự, nếu $\phi: \mathscr{F} \to \mathscr{G}$ là một cấu xạ thì tiền bó hạch $$\text{Ker}\phi: U \mapsto \text{Ker}(\phi(U))$$ cũng là một bó. Nếu $\phi$ là một đơn cấu thì nó cảm sinh một đẳng cấu giữa $\mathscr{F}$ và tiền bó ảnh $$\text{Im} \phi: U \mapsto \text{Im}(\phi(U)),$$ vì thế $\text{Im} \phi$ cũng là một bó. Tuy nhiên, nói chung thì $\text{Im} \phi$ không phải là một bó. Điều tương tự xảy ra với các tiền bó đối hạch $\text{Coker} \phi$ và thương $\mathscr{G} / \mathscr{F}$ (khi $\mathscr{F}$ là một bó con của $\mathscr{G}$.

 

Để khắc phục điều này, ta xây dựng hàm tử bó hóa (sheafification) như sau. Cho $\mathscr{F}$ là một tiền bó trên $X$. Cho $U \subseteq X$ là một tập mở. Một bộ $(\alpha_x)_{x \in U} \in \prod_{x \in U} \mathscr{F}_x$ được gọi là một mầm tương thích (compatible germ) của $\mathscr{F}$ trên $U$ nếu với mỗi $x \in U$, tồn tại lân cận mở $V \subseteq U$ của $x$ và lớp cắt $s \in \mathscr{F}(V)$ sao cho $s_y = \alpha_y$ với mọi $y \in V$. Các mầm tương thích của $\mathscr{F}$ trên $U$ lập thành một nhóm con của tích trực tiếp $\prod_{x \in U} \mathscr{F}_x$. Ta ký hiệu nhóm này bởi $\mathscr{F}^{\#}(U)$. Nếu $V \subseteq U$ là các tập mở, phép chiếu $\prod_{x \in U} \mathscr{F}_x \to \prod_{x \in V} \mathscr{F}_x$ cảm sinh một đồng cấu hiển nhiên $\mathscr{F}^{\#}(U) \to \mathscr{F}^{\#}(V)$. Dễ thấy ta có một tiền bó $$\mathscr{F}^{\#}: U \mapsto \mathscr{F}^{\#}(U).$$ Ta khẳng định rằng đây là một bó. Thật vậy, cho $U = \bigcup_{i \in I} U_i$ là một phủ mở. Cho $\alpha^i  = (\alpha^i_x)_{x \in U_i} \in \mathscr{F}^{\#}(U_i)$ với mỗi $i \in I$, sao cho $\alpha^i_x = \alpha^j_x$ với mọi $i,j \in I$ và mọi $x \in U_i \cap U_j$. Điều này cho phép ta định nghĩa bộ $\alpha = (\alpha_x)_{x \in U}$ như sau: với mỗi $x \in U$, lấy một chỉ số $i \in I$ tùy ý sao cho $x \in U_i$ và đặt $\alpha_x:=\alpha^i_x$. Hiển nhiên đây là một mầm tương thích (do tính "địa phương" của định nghĩa mầm tương thích), vậy $\alpha \in \mathscr{F}^{\#}(U)$ thỏa mãn $\alpha|_{U_i} = \alpha^i$ với mọi $i \in I$. Hiển nhiên đây là lớp cắt duy nhất thỏa mãn tính chất này.

 

Định nghĩa. Bó $\mathscr{F}^{\#}$ được gọi là bó liên kết với tiền bó $\mathscr{F}$.

Bó hóa có tính hàm tử theo nghĩa hiển nhiên: Mỗi đồng cấu $\phi: \mathscr{F} \to \mathscr{G}$ cảm sinh một đồng cấu bó $\phi^{\#}: \mathscr{F}^{\#} \to \mathscr{G}^{\#}$. Cụ thể, nếu $U$ là một tập mở của $X$ và $\alpha = (\alpha_x)_{x \in U} \in \mathscr{F}^{\#}(U)$ là một mầm tương thích thì $\phi^{\#}(\alpha) = (\phi_x(\alpha_x))_{x \in U} \in \mathscr{G}^{\#}(U)$.

 

Ta có một cấu xạ tiền bó $i: \mathscr{F} \to \mathscr{F}^{\#}$ như sau: với mỗi tập mở $U$ của $X$ và $s \in \mathscr{F}(U)$, $i(s) = (s_x)_{x \in U}$.

 

Mệnh đề. Cấu xạ $i$ cảm sinh đẳng cấu trên từng thớ. Nói riêng, nếu $\mathscr{F}$ là một bó thì $i$ là một đẳng cấu.

Chứng minh

Cố định $x \in X$. Với mỗi lân cận mở $U$ của $x$, ký hiệu $p_U: \mathscr{F}^{\#}(U) \to \mathscr{F}_x$ là phép chiếu lên tọa độ $x \in U$. Khi $U$ thay đổi, các cấu xạ $p_U$ tương thích với các đồng cấu hạn chế của $\mathscr{F}^{\#}$, vì thế chúng cảm sinh một đầu cấu $p_x: \mathscr{F}^{\#}_x \to \mathscr{F}_x$. Hợp thành $p_U \circ i(U): \mathscr{F}(U) \to \mathscr{F}_x$ là đồng cấu chính tắc $s \mapsto s_x$. Do đó $p_x \circ i_x = \text{id}_{\mathscr{F}_x}$ theo tính chất phổ dụng của đối giới hạn. Từ đó suy ra $i_x$ là một đơn cấu.

Tiếp theo, xét $\alpha \in \mathscr{F}^{\#}_x$ tùy ý. Thế thì $\alpha$ là mầm tại $x$ của một lớp cắt $\beta = (\beta_y)_{y \in U} \in \mathscr{F}^{\#}(U)$ nào đó, với $U$ là một lân cận mở của $x$. Vì $\beta$ là một mầm tương thích nên tồn tại lân cận mở $V \subseteq U$ của $x$ và lớp cắt $s \in \mathscr{F}(V)$ sao cho $s_y = \beta_y$ với mọi $y \in V$, nghĩa là $i(s)|_V = \beta|_V$. Từ đó ta có $i_x(s_x) = i(s)_x = \alpha$, vậy $i_x$ là một toàn cấu.

Nếu $\mathscr{F}$ là một bó thì $i$ là một đẳng cấu, vì tính chất "là một đẳng cấu" kiểm tra được trên thớ. $\square$

 

Tính chất phổ dụng của bó liên kết. Với mỗi cấu xạ $\phi: \mathscr{F} \to \mathscr{G}$, trong đó $\mathscr{G}$ là một bó trên $X$, tồn tại duy nhất cấu xạ $\phi': \mathscr{F}^{\#} \to \mathscr{G}$ sao cho $\phi = \phi' \circ i$.

Chứng minh

Cấu xạ bó hóa $j: \mathscr{G} \to \mathscr{G}^{\#}$ là một đẳng cấu (theo mệnh đề trước). Tính toán trực tiếp, ta có $\phi^{\#} \circ i = j \circ \phi$. Vì thế, cấu xạ $\phi'$ duy nhất thỏa mãn $\phi = \phi' \circ i$ là $\phi' = j^{-1} \circ \phi^{\#}$. $\square$

 

Như vậy, ta có một đẳng cấu tự nhiên $\text{Hom}_{\textbf{Sh}(X)}(\mathscr{F}^{\#},\mathscr{G}) \simeq \text{Hom}_{\textbf{Psh}(X)}(\mathscr{F},\mathscr{G})$. Nói cách khác, hàm tử bó hóa $(-)^{\#}: \textbf{Psh}(X) \to \textbf{Sh}(X)$ là liên hợp bên trái của hàm tử quên $\textbf{Sh}(X) \to \textbf{Psh}(X)$. Vì thế, bó hóa là một hàm tử khớp phải và bảo toàn đối giới hạn. Nếu $\phi: \mathscr{F} \to \mathscr{G}$ là một đơn cấu giữa hai tiền bó thì với mỗi $x \in X$, $\phi_x: \mathscr{F} \to \mathscr{G}$ là một đơn cấu (xem chứng minh ở Bài 3; bước này không cần dùng đến tiên đề bó của $\mathscr{F}$). Các cấu xạ bó hóa $\mathscr{F} \to \mathscr{F}^{\#}$ và $\mathscr{G} \to \mathscr{G}^{\#}$ cảm sinh đẳng cấu trên thớ, do đó $\phi_x^{\#}: \mathscr{F}^{\#}\to \mathscr{G}^{\#}$ là một đơn cấu, suy ra $\phi^{\#}$ là một đơn cấu vì $\mathscr{F}^{\#}$ và $\mathscr{G}^{\#}$ là các bó. Tóm lại, bó hóa  $(-)^{\#}: \textbf{Psh}(X) \to \textbf{Sh}(X)$ là một hàm tử khớp. Tuy nhiên, hàm tử quên $\textbf{Sh}(X) \to \textbf{Psh}(X)$ nói chung chỉ khớp trái.

 

Sử dụng tính chất phổ dụng của bó hóa, ta chứng minh được rằng $\mathbf{Sh}(X)$ là một phạm trù abel. Hơn nữa, nếu $\phi: \mathscr{F} \to \mathscr{G}$ là một đồng cấu giữa hai bó thì $(\text{Coker} \phi)^{\#}$ chính là đối hạch của $\phi$ theo nghĩa bó (i.e. trong phạm trù $\mathbf{Sh}(X)$). Tương tự, $(\text{Im} \phi^{\#}$ chính là ảnh của $\phi$ theo nghĩa bó. Nếu $\mathscr{F}$ là một bó con của $\mathscr{G}$ (nghĩa là $\mathscr{F}(U) \subseteq \mathscr{G}(U)$ với mọi tập mở $U$) thì $(\mathscr{G}/\mathscr{F})^{\#}$ chính là thương của $\mathscr{G}$ bởi $\mathscr{F}$ theo nghĩa bó.

 

Kể từ nay, ta sẽ dùng các ký hiệu $\text{Coker} \phi$, $\text{Im} \phi$ và $\mathscr{G}/\mathscr{F}$ để chỉ đối hạch, ảnh và thương theo nghĩa bó. Các đối tượng tương ứng theo nghĩa tiền bó sẽ được ký hiệu lần lượt bởi $(\text{Coker} \phi)^{\text{pre}}$, $(\text{Im} \phi)^{\text{pre}}$ và $(\mathscr{G}/\mathscr{F})^{\text{pre}}$.

 

Mệnh đề. Cho $\phi: \mathscr{F} \to \mathscr{G}$ là một cấu xạ giữa hai bó. Các khẳng định sau đây là tương đương.

1. $\phi$ là một toàn cấu (theo nghĩa bó).

2. $\phi_x: \mathscr{G}_x \to \mathscr{F}_x$ là một toàn cấu nhóm với mọi $x \in X$.

3. Với mỗi tập mở $U \subseteq X$, mỗi lớp cắt $t \in \mathscr{G}(U)$ và mỗi $x \in U$, tồn tại lân cận mở $V \subseteq U$ của $x$ và lớp cắt $s \in \mathscr{F}(V)$ sao cho $\phi(s) = t|_V$ ("một cách địa phương, mỗi lớp cắt của $\mathscr{G}$ đều là ảnh của một lớp cắt của $\mathscr{F}$").

Chứng minh

$1. \Rightarrow 2.$ Cố định $x \in X$ và đặt $A = \text{Coker} \phi_x$. Ta xây dựng một cấu xạ $\psi$ từ $\mathscr{G}$ vào bó chọc trời $i_{x,\ast} A$ như sau. Cho $U$ là một tập mở của $X$. Nếu $x \in U$, ta đặt $\psi(U): \mathscr{G}(U) \to i_{x,\ast}A(U) = A$ là hợp thành $\mathscr{G}(U) \to \mathscr{G}_x \to \text{Coker} \phi_x = A$. Trong trường hợp này, ta có biểu đồ giao hoán

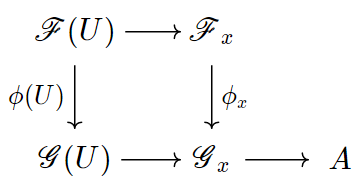
Vì hợp thành $\mathscr{F_x} \xrightarrow{\phi_x} \mathscr{G}_x \to A$ bằng $0$, nên ta có $\psi(U) \circ \phi(U) = 0$.

Nếu $x \notin U$, ta đặt $\psi(U) = 0: \mathscr{G}(U) \to i_{x,\ast}A(U) = 0$. Trong mọi trường hợp, ta có $\psi(U) \circ \phi(U) = 0$, nghĩa là $\psi \circ \phi = 0$, suy ra $\psi = 0$ vì $\phi$ là một toàn cấu. Từ đó $\psi_x = 0$. Mà $\psi_x$ chính là phép chiếu $\mathscr{G}_x \to A$, nên $\text{Coker} \phi_x = A = 0$, suy ra $\phi_x$ là một toàn cấu.

$2. \Rightarrow 3.$ Cho $U \subseteq X$ là một tập mở, $t \in \mathscr{G}(U)$ và $x \in U$. Vì $\phi_x$ là một toàn cấu nên tồn tại $\alpha \in \mathscr{F}_x$ sao cho $\phi_x(\alpha) = t_x$. Ta có thể viết $\alpha = s'_x$ với $s' \in \mathscr{F}(U')$ nào đó, và $U'$ là một lân cận mở của $x$, từ đó $t_x = \phi_x(s'_x) = \phi(s')_x$, nghĩa là tồn tại lân cận mở $V \subseteq U' \subseteq U$ của $x$ sao cho $t|_V = \phi(s')|_V$. Lấy $s = s'|_V$, ta có $t|_V = \phi(s)$.

$3. \Rightarrow 1.$ Giả sử $\psi: \mathscr{G} \to \mathscr{H}$ là một cấu xạ (trong đó $\mathscr{H}$ là một bó) sao cho $\psi \circ \phi = 0$. Cho $U$ là một tập mở của $X$ và $t \in \mathscr{G}(U)$. Với mỗi $x \in U$, tồn tại lân cận mở $U_x \subseteq U$ của $x$ và lớp cắt $s^x \in \mathscr{F}(U_x)$ sao cho $\phi(s^x) = t|_{U_x}$, suy ra $\psi(t)|_{U_x} = \psi(t|_{U_x}) = \psi(\phi(s^x)) = 0$. Mà $\{U_x\}_{x \in U}$ là một phủ mở của $U$ và $\mathscr{H}$ là một bó nên ta có $\psi(t) = 0$. Vậy $\psi = 0$, suy ra $\phi$ là một toàn cấu. $\square$

 

Từ kết quả trên, ta có mô tả khá dễ chịu sau đây cho ảnh (theo nghĩa bó) của một đồng cấu bó. Cho $\phi: \mathscr{F} \to \mathscr{G}$ là một đồng cấu bó. Ký hiệu bởi $\mathscr{I}$ tiền bó con của $\mathscr{G}$ được xây dựng như sau. Với mỗi tập mở $U \subseteq X$, $\mathscr{I}(U)$ là nhóm các lớp cắt $t \in \mathscr{G}(U)$ sao cho với mỗi $x \in U$, tồn tại lân cận mở $V \subseteq U$ của $x$ và lớp cắt $s \in \mathscr{F}(V)$ sao cho $\phi(s) = t|_V$. Tiền bó $\mathscr{I}$ là một bó; vì nếu $U = \bigcup_{i \in I} U_i$ là một phủ mở và $t_i \in \mathscr{I}(U_i) \subseteq \mathscr{G}(U_i)$ với mỗi $i \in I$ sao cho $t_i|_{U_i \cap U_j} = t_j|_{U_i \cap U_j}$ với mọi $i,j \in I$ thì ta có thể dán các lớp cắt $t_i$ thành một lớp cắt $t \in \mathscr{G}(U)$. Một cách địa phương, mỗi lớp cắt $t_i$ đều là ảnh bởi $\phi$ của một lớp cắt của $\mathscr{F}$, nên $t$ cũng vậy, nghĩa là $t \in \mathscr{I}(U)$. Hiển nhiên, cấu xạ $\phi: \mathscr{F} \to \mathscr{G}$ có một phân tích $\mathscr{F} \to \mathscr{I} \to \mathscr{G}$, trong đó $\mathscr{F} \to \mathscr{I}$ là một toàn cấu (mệnh đề trên) và $\mathscr{I} \to \mathscr{G}$ là một đơn cấu (đơn cấu theo nghĩa bó và tiền bó là như nhau!). Theo định nghĩa, $\mathscr{I}$ đẳng cấu với bó ảnh $\text{Im} \phi$.

 

Sau đây là một kết quả quan trọng.

Mệnh đề. Tính khớp của một dãy các đồng cấu bó có thể kiểm tra trên thớ.

Chứng minh

Cho $\mathscr{F} \xrightarrow{\phi} \mathscr{G} \xrightarrow{\psi} \mathscr{H}$ là một dãy các đồng cấu bó. 

Nếu dãy $\mathscr{F} \xrightarrow{\phi} \mathscr{G} \xrightarrow{\psi} \mathscr{H}$ khớp thì $\text{Ker}\psi = \text{Im} \phi$ (như những bó con của $\mathscr{G}$, ta dùng mô tả ở trên của bó ảnh $\text{Im} \phi$. Cố định $x \in X$. Bó hóa bảo toàn thớ, nên ta có $(\text{Im} \phi)^{\text{pre}}_x = (\text{Im} \phi)_x = (\text{Ker} \psi)_x$. Lấy đối giới hạn là một hàm tử khớp, nên ta có $\text{Im} \phi_x = (\text{Im} \phi)^{\text{pre}}_x = (\text{Ker} \psi)_x = \text{Ker} \psi_x$, nghĩa là dãy $\mathscr{F_x} \xrightarrow{\phi_x} \mathscr{G_x} \xrightarrow{\psi_x} \mathscr{H_x}$ khớp.

Ngược lại, giả sử dãy $\mathscr{F_x} \xrightarrow{\phi_x} \mathscr{G_x} \xrightarrow{\psi_x} \mathscr{H_x}$ khớp với mọi $x \in X$. Nói riêng, $\psi \circ \phi = 0$, vì $(\psi \circ \phi)_x = \psi_x \circ \phi_x = 0$ với mọi $x \in X$. Từ đó, ta có một đơn cấu giữa hai tiền bó $(\text{Im} \phi)^{\text{pre}} \to \text{Ker} \psi$. Theo chính chất phổ dụng, nó cảm sinh một cấu xạ giữa hai bó $\text{Im} \phi \to \text{Ker} \psi$. Đây là một đẳng cấu vì nó cảm sinh đẳng cấu trên thớ (bó hóa bảo toàn thớ). Vậy $\text{Im} \phi = \to \text{Ker} \psi$, nghĩa là dãy $\mathscr{F} \xrightarrow{\phi} \mathscr{G} \xrightarrow{\psi} \mathscr{H}$ khớp $\square$.

 

Ví dụ. Xét $X = \mathbb{C}$. Xét $\mathcal{O}$ là bó hàm chỉnh hình trên $\mathbb{C}$. Phép đạo hàm chỉnh hình cho ta một cấu xạ $\partial / \partial z: \mathcal{O} \to \mathcal{O}$. Ta có một dãy khớp các bó $\mathbb{C}$-không gian véc-tơ $$0 \to \underline{\mathbb{C}} \to \mathcal{O} \xrightarrow{\partial / \partial z} \mathcal{O} \to 0$$ (một hàm chỉnh hình có đạo hàm bằng $0$ khắp nơi khi và chỉ khi nó là hàm hằng địa phương; mọi hàm chỉnh hình đều có nguyên hàm địa phương). Ta cũng có thể chứng minh điều này bằng cách kiểm tra trên thớ (nhắc lại rằng với $a \in \mathbb{C}$ thì $\mathcal{O}_a = \mathbb{C}\{z - a\}$, vành cái chuỗi lũy thừa với tâm tại $a$ và bán kính hội tụ dương).

 

Nếu ta xét vành lớp cắt trên $U = \mathbb{C}^\times$ thì ta chỉ có một dãy khớp $$0 \to \mathbb{C} \to \mathcal{O}(\mathbb{C}^\times) \xrightarrow{\partial / \partial z} \mathcal{O}(\mathbb{C}^\times).$$ Cấu xạ cuối cùng không là một toàn cấu vì hàm $z \mapsto 1/z$ chỉnh hình trên $\mathbb{C}^\times$ nhưng không có nguyên hàm (toàn cục).

 

Tương tự, xét $\mathcal{O}^\times$ là bó hàm chỉnh hình không triệt tiêu. Hàm mũ cho ta một cấu xạ $\exp: \mathcal{O} \to \mathcal{O}^\times$. Ta có một dãy khớp các bó nhóm abel $$0 \to \underline{2\pi i \mathbb{Z}} \to \mathcal{O} \xrightarrow{\exp} \mathcal{O}^\times \to 1.$$ Nếu ta xét vành lớp cắt trên $U = \mathbb{C}^\times$ thì ta chỉ có một dãy khớp $$0 \to 2\pi i \mathbb{Z} \to \mathcal{O}(\mathbb{C}^\times) \xrightarrow{\exp} \mathcal{O}^\times(\mathbb{C}^\times).$$ Cấu xạ cuối cùng không là một toàn cấu vì hàm $z \mapsto z$ chỉnh hình và không triệt tiêu trên $\mathbb{C}^\times$ nhưng không có lô-ga-rít (toàn cục).

 

File gửi kèm

•  2.png   7.56K   64 Số lần tải

[nmlinh16]

5. Ảnh ngược

 

Ở bài này, ta cố định một ánh xạ liên tục $f: Y \to X$ giữa hai không gian tô-pô.

 

Cho $\mathscr{F}$ là một bó trên $X$. Ta muốn dùng $f$ để kéo lùi nó thành một bó trên $Y$. Xây dựng này rất giống với bó hóa.

Với mỗi tập mở $V$ của $Y$, một bộ $(\alpha_y)_{y \in V} \in \prod_{y \in V} \mathscr{F}_{f(y)}$ được gọi là một mầm $f$-tương thích của $\mathscr{F}$ trên $V$ nếu với mỗi $y \in V$, tồn tại các tập mở $U \subseteq X$ và $V' \subseteq V \cap f^{-1}(U)$ với $y \in V'$ và một lớp cắt $s \in \mathscr{F}(U)$ sao cho $\alpha_{y'} = s_{f(y')}$ với mọi $y' \in V'$. Các mầm $f$-tương tích của $\mathscr{F}$ trên $V$ lập thành một nhóm con của $\prod_{y \in V} \mathscr{F}_{f(y)}$, ta ký hiệu nhóm này bởi $f^{-1}\mathscr{F}(V)$.

Nếu $W \subseteq V$ là các tập mở của $Y$, phép chiếu $\prod_{y \in V} \mathscr{F}_{f(y)} \to \prod_{y \in W} \mathscr{F}_{f(y)}$ cảm sinh một đồng cấu hiển nhiên $f^{-1} \mathscr{F}(V) \to f^{-1} \mathscr{F}(W)$. Hiển nhiên ta có một tiền bó trên $Y$, $$f^{-1} \mathscr{F}: V \mapsto f^{-1} \mathscr{F}(V).$$ Ta khẳng định rằng đây là một bó. Thật vậy, cho $V = \bigcup_{i \in I}V_i$ là một phủ mở (gồm các tập mở của $Y$). Cho $\alpha^i = (\alpha^i_y)_{y \in V_i} \in f^{-1} \mathscr{F}(V_i)$ với mỗi $i \in I$, sao cho $\alpha^i_y = \alpha^j_y$ với mọi $i,j \in I$ và mọi $y \in V_i \cap V_j$. Điều này cho phép ta định nghĩa bộ $\alpha = (\alpha_y)_{y \in V}$ như sau. Với mỗi $y \in V$, lấy chỉ số $i \in I$ tùy ý sao cho $y \in V_i$ và đặt $\alpha_y:=\alpha^i_y$. Đây là một mầm $f$-tương thích (vì tính địa phương của định nghĩa mầm $f$-tương thích), vậy $\alpha \in f^{-1}\mathscr{F}(V)$ thỏa mãn $\alpha|_{V_i} = \alpha^i$ với mọi $i \in I$. Hiển nhiên $\alpha$ là lớp cắt duy nhất của $f^{-1}\mathscr{F}$ trên $V$ thỏa mãn tính chất này.

 

Định nghĩa. Bó $f^{-1} \mathscr{F}$ được gọi là ảnh ngược (hay kéo lùi) của bó $\mathscr{F}$ bởi $f$.

Ảnh ngược có tính hàm tử theo nghĩa hiển nhiên. Mỗi đồng cấu $\phi: \mathscr{F} \to \mathscr{F'}$ các bó trên $X$ cảm sinh một đồng cấu $f^{-1} \phi: f^{-1} \mathscr{F}  \to f^{-1} \mathscr{F}'$ các bó trên $Y$. Cụ thể, với $V$ là một tập mở của $Y$ và $\alpha = (\alpha_y)_{y \in V} \in f^{-1}\mathscr{F} (V)$ là một mầm $f$-tương thích thì $f^{-1}\phi(\alpha) = (\phi_{f(y)}(\alpha_y))_{y \in V}$.

 

Bước đầu tiên, ta sẽ chứng minh rằng phép kéo lùi bó bảo toàn thớ.

 

Cho $U$ là một tập mở của $X$. Ta có một đồng cấu liên hợp (adjunction map) $$a_U: \mathscr{F}(U) \to f^{-1} \mathscr{F} (f^{-1}(U)), \qquad s \mapsto (s_{f(y)})_{y \in f^{-1}(U)}.$$ Với mỗi $y \in f^{-1}(U)$, hợp thành của cấu xạ chính tắc $f^{-1}\mathscr{F} (f^{-1}(U)) \to (f^{-1}\mathscr{F})_y$ với $a_U$ cho ta một cấu xạ $\mathscr{F}(U) \to (f^{-1}\mathscr{F})_y$. Cố định $y$ và lấy đối giới hạn khi $U \owns f(y)$ thay đổi, ta thu được cấu xạ $a_y: \mathscr{F}_{f(y)} \to (f^{-1}\mathscr{F})_y$.

 

Mệnh đề. $a_y: \mathscr{F}_{f(y)} \to (f^{-1}\mathscr{F})_y$ là một đẳng cấu với mỗi $y \in Y$.

Chứng minh

Với mỗi lân cận mở $V$ của $y$, ký hiệu $p_V: f^{-1}\mathscr{F}(V) \to \mathscr{F}_{f(y)}$ là phép chiếu lên tọa độ $y \in V$. Khi $V$ thay đổi, các cấu xạ $p_V$ tương thích với các đồng cấu hạn chế của $f^{-1}\mathscr{F}$, vì thế chúng cảm sinh một đồng cấu $p_y: (f^{-1}\mathscr{F})_y \to \mathscr{F}_{f(y)}$. Với mỗi lân cân mở $U$ của $f(y)$, hợp thành $p_{f^{-1}(U)} \circ a_U: \mathscr{F}(U) \to \mathscr{F}_{f(y)}$ là đồng cấu chính tắc $s \mapsto s_{f(y)}$. Do đó $p_y \circ a_y = \text{id}_{\mathscr{F}_{f(y)}}$ theo tính chất phổ dụng của đối giới hạn. Nói riêng, $a_y$ là một đơn cấu.

Tiếp theo, xét $\alpha \in (f^{-1}\mathscr{F})_y$. Thế thì $\alpha$ là mầm tại $y$ của một lớp cắt $\beta = (\beta_y)_{y \in V} \in f^{-1} \mathscr{F}(V)$, với $V$ là một lân cận mở của $y$. Vì $\beta$ là một mầm $f$-tương thích nên tồn tại các tập mở $U \subseteq X$ và $V' \subseteq V \cap f^{-1}(U)$ với $y \in V'$ và một lớp cắt $s \in \mathscr{F}(U)$ sao cho $\beta_{y'} = s_{f(y')}$ với mọi $y' \in V'$, nghĩa là $a_U(s)|_{V'} = \beta|_{V'}$, từ đó $a_U(s)_y = \alpha$. Mặt khác, biểu đồ 

giao hoán, do đó $\alpha = a_U(s)_y = a_y(s_{f(y)}$, vậy $a_y$ là một toàn cấu. $\square$

 

Hệ quả. Hàm từ ảnh ngược $f^{-1}: \mathbf{Sh}(X) \to \mathbf{Sh}(Y)$ là một hàm tử khớp.

Chứng minh

Cho $\mathscr{F'} \to \mathscr{F} \to \mathscr{F''}$ là một dãy khớp các bó trên $X$. Với mỗi $y \in Y$, ta có biểu đồ giao hoán

trong đó các mũi tên dọc là các đẳng cấu cảm sinh từ các đồng cấu liên hợp. Vì tính khớp có thể kiểm tra trên thớ nên ta có dãy khớp $f^{-1}\mathscr{F'} \to f^{-1}\mathscr{F} \to f^{-1}\mathscr{F''}$. $\square$

 

Ta có một mô tả khác cho bó $f^{-1} \mathscr{F}$ như sau. Xét $\mathscr{P}$ là tiền bó trên $Y$ cho bởi $V \mapsto \varinjlim_{U \supseteq f(V)} \mathscr{F}(U)$ (các đồng cấu hạn chế được định nghĩa một cách hiển nhiên). Với $V$ là một tập mở của $Y$ vào $U \supseteq f(V)$ là một tập mở của $X$, ta có đồng cấu $\mathscr{F}(U) \xrightarrow{a_U} f^{-1} \mathscr{F}(f^{-1}U)) \xrightarrow{r_{f^{-1}(U) \to V}} f^{-1}\mathscr{F}(V)$. Chúng cảm sinh một đồng cấu $\phi(V): \mathscr{P}(V) \to f^{-1}\mathscr{F}(V)$. Khi $V$ thay đổi, ta thu được một cấu xạ giữa hai tiền bó $\phi: \mathscr{P} \to f^{-1} \mathscr{F}$.

Với $y \in Y$, ta tính thớ $\mathscr{P}_y = \varinjlim_{U \supseteq f(V), V \owns y} \mathscr{F}(U)$. Với $U$ là lân cận mở tùy ý của $Y$ thì $V = f^{-1}(U)$ là một lân cận mở của $y$ và $U \supseteq f(V)$. Do đó đối giới hạn vừa xét là cofinal, nên ta có $\mathscr{P}_y = \varinjlim_{U \owns f(y)} \mathscr{F}(U) = \mathscr{F}_{f(y)}$. 

Với $V$ là lân cận mở của $y$ và $U \supseteq f(V)$ là một tập mở trong $X$, ta có biểu đồ giao hoán

Theo mệnh đề trên thì $\phi_y = a_y$ là một đẳng cấu. Theo chính chất phổ dụng của bó liên kết, $\phi$ cảm sinh một cấu xạ $\phi': \mathscr{P}^{\#} \to f^{-1}\mathscr{F}$. Đây là một đẳng cấu, vì nó cảm sinh đẳng cấu trên từng thớ (bó hóa bảo toàn thớ). Như vậy, bó ảnh ngược $f^{-1}\mathscr{F}$ chính là bó liên kết với tiền bó $$V \mapsto \varinjlim_{U \supseteq f(V)} \mathscr{F}(U).$$

 

Ví dụ.

1. Cho $U \subseteq X$ là một tập mở $i: U \to X$ là phép bao hàm. Thế thì $i^{-1} \mathscr{F}$ là bó hạn chế $\mathscr{F}|_U$ của $\mathscr{F}$ trên $U$ cho bởi $U' \mapsto \mathscr{F}(U')$.

2. Cho $x \in X$ và $i: \{x\} \to X$ là phép bao hàm. Thế thì $i^{-1} \mathscr{F}$ là bó trên $\{x\}$ cho bởi $\varnothing \mapsto 0$ và $\{x\} \mapsto \mathscr{F}_x$.

3. Cho $Z \xrightarrow{g} Y \xrightarrow{f} X$ là các ánh xạ liên tục giữa các không gian tô-pô. Với mỗi bó $\mathscr{F}$ trên $X$, ta có đẳng cấu tự nhiên $g^{-1}(f^{-1} \mathscr{F}) \simeq (f \circ g)^{-1} \mathscr{F}$.

File gửi kèm

•  3.png   8.4K   79 Số lần tải
•  4.png   6.15K   56 Số lần tải
•  5.png   12.71K   57 Số lần tải

[nmlinh16]

6. Ảnh xuôi

 

Cho $f: Y \to X$ là một ánh xạ liên tục giữa hai không gian tô-pô. Nếu $\mathscr{G}$ là một bó trên $Y$ thì ta định nghĩa tiền bó $f_\ast \mathscr{G}$ trên $X$ bởi $f_\ast \mathscr{G}(U) = \mathscr{G}(f^{-1}(U))$. Đây là một bó, vì nếu $U = \bigcup_{i \in I} U_i$ là một phủ mở (gồm các tập mở của $X$) thì $f^{-1}(U) = \bigcup_{i \in I}f^{-1}(U_i)$ là một phủ mở (gồm các tập mở của $Y$); sau đó ta áp dụng tiên đề dán cho bó $\mathscr{G}$ trên phủ mở này để chứng minh tiên đề dán cho tiền bó $f_\ast \mathscr{G}$.

Xây dựng trên có tính hàm tử: Nếu $\phi: \mathscr{G} \to \mathscr{G}'$ là một đồng cấu giữa hai bó trên $Y$ thì ta có một đồng cấu bó $f_\ast \phi: f_\ast \mathscr{G} \to f_\ast \mathscr{G}'$ giữa hai bó trên $X$, trong đó $f_\ast \phi(U) = \phi(f^{-1}(U)): \mathscr{G}(f^{-1}(U)) \to \mathscr{G}'(f^{-1}(U))$ với mọi tập mở $U$ của $X$.

 

Cho $\mathscr{F}$ là một bó trên $X$. Ở bài trước, ta đã xây dựng đồng cấu liên hợp $$a(U): \mathscr{F}(U) \to f^{-1} \mathscr{F}(f^{-1}(U)) = f_\ast f^{-1} \mathscr{F}(U), \qquad s \mapsto (s_{f(y)})_{y \in f^{-1}(U)}$$ với mỗi tập mở $U$ của $X$. Khi $U$ thay đổi, ta thu được cấu xạ liên hợp $a: \mathscr{F} \to f_\ast f^{-1} \mathscr{F}$ giữa hai bó trên $X$. Cho $\mathscr{G}$ là một bó trên $Y$. Ta xây dựng đồng cấu $$\eta: \text{Hom}_{\mathbf{Sh}(Y)}(f^{-1} \mathscr{F}, \mathscr{G}) \to \text{Hom}_{\mathbf{Sh}(X)}(\mathscr{F},f_\ast \mathscr{G}), \qquad \phi \mapsto f_\ast \phi \circ a.$$

 

Hệ quả. $\eta$ là một đẳng cấu, tự nhiên theo $\mathscr{F}$ và $\mathscr{G}$.

Chứng minh

$\eta$ là một đơn cấu. Cho $\phi: \mathscr{F}^{-1} \to \mathscr{G}$ là một cấu xạ. Cố định $y \in Y$. Với mỗi lân cân mở $U$ của $f(y)$, ta có biểu đồ giao hoán

Lấy giới hạn khi $U \owns f(y)$ thay đổi, ta thu được biểu đồ giao hoán.

Ta đã biết rằng biết rằng $a_y$ là một đẳng cấu. Nếu $\eta(\phi) = 0$ thì từ đây ta suy ra $\phi_y = 0$ với mọi $y \in Y$, do đó $\phi = 0$.

 

$\eta$ là một toàn cấu. Cho $\psi: \mathscr{F} \to f_\ast\mathscr{G}$ là một cấu xạ. Với mỗi $y \in Y$, xét cấu xạ $b_y: (f_\ast \mathscr{G})_{f(y)} \to \mathscr{G}_y$ trong biểu đồ giao hoán ở trên. Cụ thể, nếu $U$ là một lân cận mở của $f(y)$ và $s \in f_\ast \mathscr{G}(U) = \mathscr{G}(f^{-1}(U))$ thì $b_y(s_{f(y)}) = s_y$. Ta xây dựng cấu xạ $\phi: f^{-1} \mathscr{F} \to \mathscr{G}$ như sau. Cho $V$ là một tập mở của $Y$ và $\alpha = (\alpha_y)_{y \in V}) \in f^{-1} \mathscr{F}(V)$ là một mầm $f$-tương thích. Khi đó $(b_y(\psi_{f(y)}(\alpha_y)))_{y \in V} \in \prod_{y \in V} \mathscr{G}_y$ là một mầm tương thích. Vì $\mathscr{G}$ là một bó nên tồn tại một lớp cắt suy nhất, mà ta ký hiệu là $\phi(\alpha) \in \mathscr{G}(U)$, sao cho $\phi(\alpha)_y = b_y(\psi_{f(y)}(\alpha_y))$ với mọi $y \in V$.

Ta chứng minh rằng $\psi = f_\ast \phi \circ a: \mathscr{F} \to f_\ast \mathscr{G}$. Thật vậy, cho $U$ là một tập mở của $X$ và $s \in \mathscr{F}(U)$. Ta cần chứng minh rằng $\psi(s) = \phi(a(s)) \in \mathscr{G}(f^{-1}(U))$: với mọi $y \in f^{-1}(U)$, ta có $$\phi(a(s))_y = b_y(\psi_{f(y)}(a(s)_y)) = b_y(\psi_{f(y)}(s_{f(y)})) = b_y(\psi(s)_{f(y})) = \psi(s)_{y},$$ do đó $\psi(s) = \phi(a(s))$. Vậy $\psi = f_\ast \phi \circ a = \eta(\phi)$.

 

$\eta$ tự nhiên theo $\mathscr{F}$ và $\mathscr{G}$. Cho $\psi: \mathscr{F'} \to \mathscr{F}$ là một đồng cấu giữa hai bó trên $X$ và $\theta: \mathscr{G} \to \mathscr{G'}$ là một đồng cấu giữa hai bó trên $Y$. Ta cần chứng minh rằng biểu đồ

giao hoán. Cho $\phi: f^{-1}\mathscr{F} \to \mathscr{G}$ là một cấu xạ. Ta cần chứng minh rằng $$f_\ast \theta \circ f_\ast \phi \circ a \circ \psi = f_\ast(\theta \circ \phi \circ f^{-1}\psi) \circ a.$$ Vì tính hàm tử của $f_\ast$ nên ta chỉ còn phải chứng minh rằng $a \circ \psi = f_\ast f^{-1} \psi \circ a: \mathscr{F'} \to f_\ast f^{-1} \mathscr{F}$. Đây chính là tính tự nhiên của cấu xạ liên hợp $a$. $\square$

 

Mệnh đề. Ảnh xuôi $f_\ast$ là liên hợp bên phải của hàm tử ảnh ngược $f^{-1}$. Nói riêng, $f_\ast$ khớp trái.

 

Ví dụ. 

1. Cho $Z \xrightarrow{g} Y \xrightarrow{f} X$ là các ánh xạ liên tục giữa các không gian tô-pô. Từ định nghĩa của $f_\ast$ và $g_\ast$, ta có $(f \circ g)_\ast = f_\ast \circ g_\ast: \mathbf{Sh}(Z) \to \mathbf{Sh}(X)$ một cách hiển nhiên. Từ đây, ta có một chứng minh đơn giản rằng $(f \circ g)^{-1} \simeq g^{-1} \circ f^{-1}$. Thật vậy, cho $\mathscr{F}$ là một bó trên $X$. Với mọi bó $\mathscr{H}$ trên $Z$, ta có các đẳng cấu tự nhiên (theo $\mathscr{H})$ $$\text{Hom}_{\mathbf{Sh}(Z)}((f \circ g)^{-1} \mathscr{F}, \mathscr{H}) = \text{Hom}_{\mathbf{Sh}(X)}(\mathscr{F}, (f \circ g)_\ast \mathscr{H}) = \text{Hom}_{\mathbf{Sh}(X)}(\mathscr{F}, f_\ast g_\ast \mathscr{H}) = \text{Hom}_{\mathbf{Sh}(Y)}(f^{-1} \mathscr{F}, g_\ast \mathscr{H}) = \text{Hom}_{\mathbf{Sh}(Y)}(g^{-1} f^{-1} \mathscr{F}, \mathscr{H}),$$ từ đó $(f \circ g)^{-1} \mathscr{F} \simeq g^{-1} f^{-1} \mathscr{F}$ theo bổ đề Yoneda. Đẳng cấu này tự nhiên theo $\mathscr{F}$ vì các đẳng cấu ở trên đều như vậy, do đó hai hàm tử $(f \circ g)^{-1}$ và $g^{-1} \circ f^{-1}$ đẳng cấu.
2. Cho $x \in X$ và $i_x: \{x\} \to X$ là phép bao hàm. Cho $A$ là một nhóm abel, mà ta có thể xem là bó $$\varnothing \mapsto 0, \qquad \{x\} \mapsto A$$ trên $X$. Khi đó đẩy xuôi $i_{x,\ast} A$ chính là bó chọc trời tại $x$ của $X$.

File gửi kèm

•  6.png   16.37K   58 Số lần tải
•  7.png   12.68K   55 Số lần tải
•  8.png   14.23K   57 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi nmlinh16: 26-05-2021 - 17:09

[nmlinh16]

7. Đối đồng điều

 

Cho $X$ là một không gian tô-pô.

 

Mệnh đề. Phạm trù $\mathbf{Sh}(X)$ các bó trên $X$ có đủ nội xạ.

Chứng minh

Cho $\mathscr{F}$ là một bó trên $X$. Với mỗi $x \in X$, nhúng $\mathscr{F}_x$ vào một nhóm abel chia được (i.e. nội xạ) $D_x$. Ta định nghĩa tiền bó $\mathscr{I}$ trên $X$ bởi $U \mapsto \prod_{x \in U} D_x$, trong đó các đồng cấu hạn chế là các phép chiếu. Dễ thấy $\mathscr{I}$ là một bó.

Vì $\mathscr{F}$ là một bó nên hợp thành $\mathscr{F}(U) \to \prod_{x \in U} \mathscr{F}_x \hookrightarrow \prod_{x \in U} D_x = \mathscr{I}(U)$ là một đơn cấu với mỗi tập mở $U$ của $X$. Khi $U$ thay đổi, ta thu được một đơn cấu $\mathscr{F} \hookrightarrow \mathscr{I}$. 

Ta chỉ còn phải chứng minh rằng $\mathscr{I}$ là một bó nội xạ. Cho $\phi: \mathscr{G} \to \mathscr{H}$ là một đơn cấu giữa hai bó trên $X$, và $\psi: \mathscr{G} \to \mathscr{I}$ là một cấu xạ tùy ý. Ta cần xây dựng cấu xạ $\theta: \mathscr{H} \to \mathscr{I}$ sao cho $\theta \circ \phi = \psi$. Cố định $x \in X$. Các phép chiếu $\mathscr{I}(U) \to D_x$ (với $U$ là lân cận mở của $x$) cảm sinh một đồng cấu $j_x: \mathscr{I}_x \to D_x$. Cụ thể, nếu $U$ là một lân cận mở của $x$ và $\alpha = (d_x)_{x \in U} \in \mathscr{I}(U)$ thì $j_x(\alpha_x) = d_x$ (nói cách khác, $\alpha = (j_x(\alpha_x))_{x \in U}$). Vì $\theta_x: \mathscr{G}_x \to \mathscr{H}_x$ là một đơn cấu và $D_x$ là một nhóm abel chia được nên tồn tại cấu xạ $\theta^x: \mathscr{H}_x \to D_x$ sao cho $\theta^x \circ \phi_x = j_x \circ \psi_x$. Với mỗi tập mở $U$ của $X$, ký hiệu bởi $\theta(U)$ đồng cấu hợp thành $\mathscr{H}(U) \to \prod_{x \in U} \mathscr{H}_x \xrightarrow{\prod_{x \in U} \theta^x} \prod_{x \in U} D_x = \mathscr{I}(U)$. Khi $U$ thay đổi, ta thu được một cấu xạ $\theta: \mathscr{H} \to \mathscr{I}$. Với mỗi $s \in \mathscr{G}(U)$, ta có $$\theta(\phi(s)) = (\theta^x(\phi(s)_x))_{x \in U} = (\theta^x(\psi_x(s_x)))_{x \in U} = (j_x(\psi_x(s_x)))_{x \in U} = (j_x(\psi(s)_x)_{x \in U} = \phi(s).$$ Vậy $\theta \circ \psi = \phi$. $\square$

 

Hệ quả. Phạm trù $\mathbf{Psh}(X)$ các tiền bó trên $X$ có đủ nội xạ. Hàm tử quên $\iota: \mathbf{Sh}(X) \to \mathbf{Psh}(X)$ bảo toàn nội xạ.

Chứng minh

Cho $\mathscr{I}$ là một bó nội xạ trên $X$. Ta có đẳng cấu tự nhiên $\text{Hom}_{\mathbf{Psh}(X)}(-,\mathscr{I}) = \text{Hom}_{\mathbf{Sh}(X)}((-)^{\#},\mathscr{I})$. Vì bó hóa $(-)^{\#}$ và $\text{Hom}_{\mathbf{Sh}(X)}(-,\mathscr{I})$ là các hàm tử khớp nên $\text{Hom}_{\mathbf{Psh}(X)}(-,\mathscr{I})$ cũng vậy, nghĩa là $I$ cũng nội xạ với tư cách là một tiền bó. Ngoài ra, nếu $\mathscr{P}$ là một tiền bó bất kỳ trên $X$ thì ta có thể nhúng bó $\mathscr{P}^{\#}$ vào một bó nội xạ $\mathscr{I}$. Tính đơn cấu theo nghĩa tiền bó kiểm tra được trên thớ, và bó hóa bảo toàn thớ, nên tiền bó $\mathscr{P}$ nhúng vào tiền bó nội xạ $\mathscr{I}$ qua cấu xạ hợp thành $\mathscr{P} \xrightarrow{i} \mathscr{P}^{\#} \to \mathscr{I}$. $\square$

 

Hàm tử quên $\iota: \mathbf{Sh}(X) \to \mathbf{Psh}(X)$ là liên hợp bên phải của hàm tử bó hóa $(-)^{\#}: \mathbf{Psh}(X) \to \mathbf{Sh}(X)$ nên là một hàm tử khớp trái. Cụ thể, nếu $0 \to \mathscr{F} \xrightarrow{\phi} \mathscr{G} \xrightarrow{\psi} \mathscr{H}$ là một dãy khớp các bó trên $X$ thì dãy nó cũng là một dãy khớp các tiền bó. Vì $\phi$ là một đơn cấu nên tiền bó ảnh $U \mapsto \text{Im}\phi(U)$ là một bó, do đó $\text{Im} (\phi(U)) = \text{Im} \phi (U) = \text{Ker} \psi(U) = \text{Ker} (\psi(U))$, nghĩa là ta có dãy khớp $0 \to \mathscr{F}(U) \xrightarrow{\phi(U)} \mathscr{G}(U) \xrightarrow{\psi(U)} \mathscr{H}(U)$. Tóm lại, hàm tử lớp cắt $$\Gamma(U,-): \mathbf{Sh}(X) \to \mathbf{Ab}, \qquad \mathscr{F} \mapsto \mathscr{F}(U)$$ khớp trái. Vì $\mathbf{Sh}(X)$ có đủ nội xạ, ta có thể định nghĩa các hàm tử dẫn xuất phải $$\text{H}^q(U,-):=\text{R}^q \Gamma(U,-), \qquad q \ge 0.$$

 

Định nghĩa. Cho $\mathscr{F}$ là một bó trên $X$ và $U$ là một tập mở của $X$. Với $q \ge 0$, nhóm $\text{H}^q(U,\mathscr{F})$ được gọi là nhóm đối đồng điều thứ $q$ của $U$ với hệ số trong $\mathscr{F}$.

 

Vì là những hàm tử dẫn xuất, các hàm tử đối đồng điều $\text{H}^q(U,\mathscr{F})$ thỏa mãn các tính chất tổng quát từ đại số đồng điều.

1. Để tính $\text{H}^q(U,\mathscr{F})$, chọn một giải nội xạ $$0 \to \mathscr{F} \to \mathscr{I}^0 \xrightarrow{d^0} \mathscr{I}^1 \xrightarrow{d^1} \cdots.$$ Áp dụng hàm tử khớp trái $\Gamma(U,-)$, ta thu được phức $$0 \to \mathscr{I}^0(U) \xrightarrow{d^0(U)} \mathscr{I}^1(U) \xrightarrow{d^0(U)} \cdots,$$ và khi đó $$\text{H}^0(U,\mathscr{F}) = \text{Ker}(d^0(U)) = \mathscr{F}(U), \qquad \text{H}^q(U,\mathscr{F}) = \frac{\text{Ker}(d^q(U))}{\text{Im}(d^{q-1}(U))}, \qquad q \ge 1.$$
2. Một dãy khớp ngắn $0 \to \mathscr{F} \to \mathscr{G} \to \mathscr{H} \to 0$ các bó trên $X$ cảm sinh một dãy khớp dài $$0 \to \mathscr{F}(U) \to \mathscr{G}(U) \to \mathscr{H}(U) \to \text{H}^1(U,\mathscr{F}) \to \text{H}^1(U,\mathscr{G}) \to \text{H}^1(U,\mathscr{H}) \to \cdots$$
3. Một bó $\mathscr{A}$ được gọi là $U$-acyclic nếu $\text{H}^q(U,\mathscr{A}) = 0$ với mọi $q \ge 1$. (nghĩa là $\mathscr{A}$ là $\Gamma(U,-)$-acyclic). Các bó nội xạ đều $U$-acyclic.
4. Các hàm tử $\text{H}^q(U,\mathscr{F})$ được định nghĩa thông qua giải nội xạ, nhưng để tính chúng thì ta chỉ cần sử dụng giải $U$-acyclic (định lý đẳng cấu de Rham-Weil). Thật vậy, trước hết nhận xét rằng nếu $0 \to \mathscr{F} \to \mathscr{G} \to \mathscr{H} \to 0$ là một dãy khớp ngắn các bó trên $X$, trong đó $\mathscr{G}$ là $U$-acyclic thì ta có dãy khớp dài $$\cdots \to \text{H}^q(U,\mathscr{G}) \to \text{H}^{q}(U,\mathscr{H}) \to \text{H}^{q+1}(U,\mathscr{F}) \to \text{H}^{q+1}(U,\mathscr{G}) \to \cdots$$ Vì $\text{H}^q(U,\mathscr{G}) = 0$ với mọi $q \ge 1$ nên ta có $\text{H}^1(U,\mathscr{F}) = \text{Coker}(\mathscr{G}(U) \to \mathscr{H}(U))$ và $\text{H}^{q+1}(U,\mathscr{F}) = \text{H}^q(U,\mathscr{H})$ với mọi $q \ge 1$. Bây giờ, giả sử $$0 \to \mathscr{F} \to \mathscr{A^0} \to \mathscr{A^1} \to \cdots$$ là một dãy khớp dài, trong đó mỗi $\mathscr{A}^q$ đều $U$-acyclic. Ta chẻ nó thành các dãy khớp ngắn $$0 \to \mathscr{F} \to \mathscr{A^0} \to \mathscr{I}^0 \to 0$$ $$0 \to \mathscr{I}^0 \to \mathscr{A}^1 \to \mathscr{I}^1 \to 0$$ $$\vdots$$ với $\mathscr{I}^q = \text{Im}(\mathscr{A}^q \to \mathscr{A}^{q+1}) = \text{Ker}(\mathscr{A}^{q+1} \to \mathscr{A}^{q+2})$. Từ nhận xét trên, ta có $$\text{H}^q(U,\mathscr{F}) = \text{H}^{q-1}(U,\mathscr{I}^0) = \cdots = \text{H}^{1}(U,\mathscr{I}^{q-2}) = \text{Coker}(\mathscr{A}^{q-1}(U) \to \mathscr{I}^{q-1}(U)).$$ Vì $\Gamma(U,-)$ khớp trái nên $\mathscr{I}^{q-1}(U) = \text{Ker}(\mathscr{A}^q(U) \to \mathscr{A}^{q+1}(U))$. Tương tự, $\mathscr{I}^{q-1}(U) \to \mathscr{A}^q(U)$ là một đơn cấu, nên $\text{Im}(\mathscr{A}^{q-1}(U) \to \mathscr{I}^{q-1}(U)) = \text{Im}(\mathscr{A}^{q-1}(U) \to \mathscr{A}^{q}(U))$. Do đó, $$\text{H}^q(U,\mathscr{F}) = \text{Coker}(\mathscr{A}^{q-1}(U) \to \mathscr{I}^{q-1}(U)) = \frac{\mathscr{I}^{q-1}(U)}{\text{Im}(\mathscr{A}^{q-1}(U) \to \mathscr{I}^{q-1}(U))} = \frac{\text{Ker}(\mathscr{A}^q(U) \to \mathscr{A}^{q+1}(U))}{\text{Im}(\mathscr{A}^{q-1}(U) \to \mathscr{A}^{q}(U))}$$ với mọi $q \ge 1$.

Nhắc lại rằng hàm tử quên $\iota: \mathbf{Sh}(X) \to \mathbf{Psh}(X)$ khớp trái. Với $q \ge 0$, ta có thể xét hàm tử dẫn xuất bên phải thứ $q$ của $\iota$, $$\mathcal{H}^q:=\text{R}^q \iota.$$

Ta sẽ chỉ rằng rằng nếu $\mathscr{F}$ là một bó trên $X$ thì $\mathcal{H}^q(\mathscr{F})$ chính là tiền bó $\text{H}^q(-,\mathscr{F}): U \mapsto \text{H}^q(U,\mathscr{F})$. 

 

Mệnh đề. Cho $\mathscr{F}$ là một bó trên $X$ và $U$ là một tập mở của $X$. Với $q \ge 0$, ta có một đẳng cấu tự nhiên $$\mathcal{H}^q(\mathscr{F})(U) = \text{H}^q(U,\mathscr{F}).$$

Chứng minh

Ta sử dụng lý thuyết về $\partial$-hàm tử, tham khảo Tôhoku paper của Grothendieck.

Nếu $0 \to \mathscr{F} \to \mathscr{G} \to \mathscr{H} \to 0$ là một dãy khớp ngắn các bó trên $X$ thì với mọi tập mở $U$, ta có khớp dài các nhóm abel, $$0 \to \mathscr{F}(U) \to \mathscr{G}(U) \to \mathscr{H}(U) \to \text{H}^1(U,\mathscr{F}) \to \text{H}^1(U,\mathscr{G}) \to \text{H}^1(U,\mathscr{H}) \to \cdots$$ Dãy khớp dài này tự nhiên theo $U$, vì thế cho ta một dãy khớp dài các tiền bó trên $X$, $$0 \to \mathscr{F} \to \mathscr{G} \to \mathscr{H} \to \text{H}^1(-,\mathscr{F}) \to \text{H}^1(-,\mathscr{G}) \to \text{H}^1(-,\mathscr{H}) \to \cdots$$ Nói riêng, ta có các đồng cấu nối $\text{H}^q(-,\mathscr{G}) \to \text{H}^{q+1}(-,\mathscr{F})$. Các hàm tử $\mathscr{F} \mapsto \text{H}^q(-,\mathscr{F})$ cùng với các đồng cấu nối này tạo thành một $\partial$-hàm tử từ $\mathbf{Sh}(X)$ vào $\mathbf{Psh}(X)$, trong đó $\text{H}^0 = \iota$. Mặt khác, nếu $\mathscr{I}$ là một bó nội xạ trên $X$ thì $\text{H}^q(-,\mathscr{I}) = 0$ với mọi $q \ge 1$, vì thế $\partial$-hàm tử nói trên là khớp và phổ dụng, và do đó trùng với các hàm tử dẫn xuất $\text{R}^q \iota = \mathcal{H}^q$. $\square$

 

 

Cho $f: Y \to X$ là một ánh xạ liên tục giữa các không gian tô-pô. Ảnh xuôi $f_\ast: \mathbf{Sh}(Y) \to \mathbf{Sh}(X)$ là một hàm tử khớp trái (vì nó là liên hợp bên phải của hàm tử ảnh ngược $f^{-1}: \mathbf{Sh}(X) \to \mathbf{Sh}(Y)$.

 

Định nghĩa. Với $q \ge 0$, ta gọi dẫn xuất bên phải thứ $q$ của $f_\ast$, $$\text{R}^q f_\ast: \mathbf{Sh}(Y) \to \mathbf{Sh}(X)$$ là hàm tử ảnh xuôi bậc cao thứ $q$ (higher direct image).

 

Mệnh đề. Cho $\mathscr{G}$ là một bó trên $Y$. Khi đó $\text{R}^q f_\ast \mathscr{G}$ là bó liên kết với tiền bó $U \mapsto \text{H}^q(f^{-1}(U),\mathscr{G})$ trên $X$. 

Chứng minh

Trước hết, ta định nghĩa hàm tử ảnh xuôi trên tiền bó $f_p: \mathbf{Psh}(Y) \to \mathbf{Psh}(X)$ một cách hoàn toàn tương tự như $f_\ast$, $$f_p \mathscr{P} (U) = \mathscr{P}(f^{-1}(U)).$$ Đây là một hàm tử khớp (tính khớp theo nghĩa tiền bó có thể kiểm tra trên từng tập mở. Nhắc lại rằng bó hóa $(-)^{\#}: \mathbf{Psh}(X) \to \mathbf{Sh}(X)$ là một hàm tử khớp, do đó hàm tử $(-)^{\#} \circ f_p: \mathbf{Psh}(Y) \to \mathbf{Sh}(X)$ khớp. Hàm tử quên $\iota: \mathbf{Sh}(Y) \to \mathbf{Psh}(Y)$ gửi mỗi bó nội xạ vào một tiền bó nội xạ trên $Y$, nói riêng là $((-)^{\#} \circ f_p)$-acyclic.

Mặt khác, rõ ràng $f_p \circ \iota = \iota \circ f_\ast$, nghĩa là nếu $\mathscr{G}$ là một bó trên $Y$ thì $f_\ast \mathscr{G} = f_p \mathscr{G} = (f_p \iota \mathscr{G})^{\#}$. Nói cách khác, hàm tử ảnh xuôi $f_\ast$ phân tích thành $$\mathbf{Sh}(Y) \xrightarrow{\iota} \mathbf{Psh}(Y) \xrightarrow{(-)^{\#} \circ f_p} \mathbf{Sh}(X).$$ Vì thế ta có dãy phổ Grothendieck $$E_2^{pq} = \text{R}^p((-)\# \circ f_p)(\mathcal{H}^q(\mathscr{G})) \Rightarrow \text{R}^q f_\ast \mathscr{G}.$$ Dãy phổ này suy biến, cụ thể là $E_2^{pq} = 0$ với mọi $p > 0$, vì $(-)^{\#} \circ f_p$ là một hàm tử khớp. Từ đó suy ra rằng đồng cấu edge $$\text{R}^q f_\ast \mathscr{G} \to (f_p \mathcal{H}^q(\mathscr{G}))^{\#}$$ là một đẳng cấu với mọi $q \ge 0$. Nói cách khác, $\text{R}^q f_\ast \mathscr{G}$ là tiền bó liên kết với bó $$U \mapsto f_p  \mathcal{H}^q(\mathscr{G})(U) = \text{H}^q(f^{-1}(U),\mathscr{G})$$ trên $X$. $\square$

 

Một tính chất khác của ảnh xuôi đó là bảo toàn nội xạ. Thật vậy, cho $\mathscr{I}$ là một bó nội xạ trên $Y$. Ta có đẳng cấu tự nhiên $\text{Hom}_{\mathbf{Sh}(X)}(-,f_\ast \mathscr{I}) = \text{Hom}_{\mathbf{Sh}(Y)}(f^{-1}(-),\mathscr{I})$. Vì ảnh ngược $f^{-1}$ và $\text{Hom}_{\mathbf{Sh}(Y)}(-,\mathscr{I})$ là các hàm tử khớp nên $\text{Hom}_{\mathbf{Sh}(X)}(-,f_\ast\mathscr{I})$ cũng vậy, nghĩa là $f_\ast \mathscr{I}$ là một bó nội xạ trên $X$.

 

Chẳng hạn, nếu $Z \xrightarrow{g} Y \xrightarrow{f} X$ là các ánh xạ liên tục giữa các không gian tô-pô thì $g_\ast$ gửi mỗi bó nội xạ trên $Z$ vào một bó $f_\ast$-acyclic trên $Y$. Từ đó ta có dãy phổ Grothendieck $$E_2^{pq} = (\text{R}^p f_\ast(\text{R}^q g_\ast\mathscr{H})) \Rightarrow \text{R}^{p+q}(f \circ g)_\ast \mathscr{H}$$ với mỗi bó $\mathscr{H}$ trên $Z$.

 

Cho $f: Y \to X$ là một ánh xạ liên tục giữa hai không gian tô-pô. Với mỗi tập mở $U$ của $X$, ta có $\Gamma(f^{-1}(U),-) = \Gamma(U,-) \circ f_\ast$. Mặt khác, $f_\ast$ gửi mỗi bó nội xạ trên $Y$ vào một bó nội xạ (nói riêng là $U$-acyclic) trên $X$. Do đó ta có dãy phổ $$E^{pq}_2 = \text{H}^p(U, \text{R}^q f_\ast \mathscr{G}) \Rightarrow \text{H}^{p+q}(f^{-1}(U), \mathscr{G})$$ với mỗi bó $\mathscr{G}$ trên $Y$, được gọi là dãy phổ Leray.

Bài viết đã được chỉnh sửa nội dung bởi nmlinh16: 26-05-2021 - 21:49

[nmlinh16]

8. Bó flasque

 

Cho $X$ là một không gian tô-pô. Một bó $\mathscr{F}$ trên $X$ được gọi là flasque (hoặc flabby) (nhũn?) nếu các đồng cấu hạn chế của nó là các toàn cấu. Dễ thấy điều này tương đương với việc mọi lớp cắt của $\mathscr{F}$ đều là hạn chế của một lớp cắt toàn cục.

 

Mệnh đề. Cho $0 \to \mathscr{F} \xrightarrow{\phi} \mathscr{G} \xrightarrow{\psi} \mathscr{H} \to 0$ là một dãy khớp các bó trên $X$, trong đó $\mathscr{F}$ là flasque. Thế thì dãy trên cũng khớp trong phạm trù các tiền bó

Chứng minh

Đây là một định lý trong ZFC. Cho $U$ là một tập mở, ta cần chứng minh rằng dãy $0 \to \mathscr{F}(U) \xrightarrow{\phi(U)} \mathscr{G}(U) \xrightarrow{\psi(U)} \mathscr{H}(U) \to 0$ khớp. Tính khớp trái đã được đảm bảo bởi hàm tử $\Gamma(U,-)$ nên ta chỉ cần chứng minh rằng $\psi(U)$ là một toàn cấu.

Cố định $t \in \mathscr{H}(U)$. Xét tập hợp $S$ các bộ $(s,V)$ với $V \subseteq U$ là một tập mở và $s \in \mathscr{G}(V)$ sao cho $\psi(s)| = t|_V$. Ta có thể giả sử rằng $U$ khác rỗng. Thế thì tập hợp $S$ khác rỗng vì $\psi$ cảm sinh toàn cấu trên từng thớ. Xét quan hệ thứ tự $\le$ trên $S$ sao cho $(s,V) \le (s',V')$ khi và chỉ khi $V \subseteq V'$ và $s'|_V = s$. Nếu một họ $\{(s_i,V_i)\}_{i \in I}$ các phần tử của $S$ được sắp thứ tự toàn phần thì ta có thể dán các lớp cắt $s_i$ thành một lớp cắt $s$ của $\mathscr{G}$ trên $V:=\bigcup_{i \in I} V_i \subseteq U$. Ta có $\psi(s)|_{V_i} = \psi(s|_{V_i}) = \psi(s_i) = t|_{V_i}$ với mọi $i \in I$, suy ra $\psi(s) = t|V$, vậy $(s,V) \in S$. Rõ ràng $(s_i,V_i) \le (s,V)$ với mọi $i \in I$.

Theo bổ đề Zorn, $S$ có một phần tử tối đại $(s,V)$. Ta khẳng định rằng $V = U$. Thật vậy, xét $x \in U$. Vì $\psi_x$ là một toàn cấu nên tồn tại $\alpha \in \mathscr{G}_x$ sao cho $\psi_x(\alpha) = t_x$. Ta có thể viết $\alpha = r_x$, với $W \in U$ là một lân cận mở của $x$ và $r \in \mathscr{G}(W)$. Thế thì $\psi(r)_x = \psi_x(r_x) = \psi_x(\alpha) = t_x$. Thu nhỏ $W$ nếu cần thiết, ta có thể giả sử rằng $\psi(r)|_W = t|_W$. Bây giờ, $\psi(s|_{V \cap W}) = t|_{W \cap W} = \psi(r|_{V \cap W})$, nên $s|_{V \cap W} = r|_{V \cap W} + \phi(v)$ với $v \in \mathscr{V \cap W}$ nào đó. Vì $\mathscr{F}$ là flasque nên tồn tại lớp cắt $w \in \mathscr{W}$ sao cho $w|_{V \cap W} = v$. Thay $r$ bởi $r - \phi(w)$ (ta vẫn có $\psi(r) = t|_W$ thì $\psi \circ \phi = 0$), ta suy ra $s|_{V \cap W} = r|_{V \cap W}$. Do đó $s$ và $r$ có thể dán thành một lớp cắt $s' \in \mathscr{G}(V \cup W)$. Nói riêng, $(s,V) \le (s', V \cup W)$, do đó $V \cup W = V$ vì $(s,V)$ là một phần tử tối đại, nghĩa là $x \in W \subseteq V$. $\square$

 

Hệ quả. Cho  $0 \to \mathscr{F} \xrightarrow{\phi} \mathscr{G} \xrightarrow{\psi} \mathscr{H} \to 0$ là một dãy khớp các bó trên $X$, trong đó $\mathscr{F}$ và $\mathscr{G}$ là flasque. Khi đó $\mathscr{H}$ là flasque.

Chứng minh

Dùng bổ đề 5 trong đại số đồng điều. $\square$

 

Xây dựng Godement. Cho $\mathscr{F}$ là một bó bất kỳ trên $X$. Tiền bó $C^0 \mathscr{F}$ trên $X$ cho bởi $U \mapsto \prod_{x \in U} \mathscr{F}_x$ (các đồng cấu hạn chế là các phép chiếu) hiển nhiên là một bó flasque. Với mỗi tập mở $U$, $\mathscr{F}(U) \to C^0\mathscr{F}(U)$ là một đơn cấu, vì thế ta có một đơn cấu bó $\mathscr{F} \hookrightarrow C^0\mathscr{F}$. Vậy, mọi bó đều nhúng được vào một bó flasque. 

 

Mệnh đề. Mỗi bó nội xạ đều flasque.

Chứng minh

Cho $\mathscr{F}$ là một bó nội xạ trên $X$. Nhúng $\mathscr{F}$ vào một bó flasque $\phi: \mathscr{F} \hookrightarrow \mathscr{G}$. Vì $\mathscr{F}$ nội xạ nên $\phi$ có một rút gọn $\psi: \mathscr{G} \to \mathscr{F}$. Nói riêng, với mọi tập mở $U$ thì $\psi(U) \circ \phi(U) = \text{id}_{\mathscr{F}(U)}$, nên $\psi(U)$ là một toàn cấu. Với $V \subseteq U$ là các tập mở của $X$, ta có biểu đồ giao hoán 

Vì $\psi(U)$, $\psi(V)$ và hạn chế $\mathscr{G}(U) \to \mathscr{G}(V)$ là các toàn cấu nên $\mathscr{F}(U) \to \mathscr{F}(V)$ cũng là một toàn cấu. $\square$

 

Mệnh đề. Mỗi bó flasque đều acyclic trên từng tập mở. Nói riêng, đối đồng điều bó có thể tính được bằng giải flasque.

Chứng minh

Cho $\mathscr{F}$ là một bó flasque trên $X$. Nhúng $\mathscr{F}$ vào một bó nội xạ $\mathscr{G}$ và gọi $\mathscr{H}$ là bó thương $\mathscr{G}/\mathscr{F}$. Khi đó ta có dãy khớp $$0 \to \mathscr{F} \to \mathscr{G} \to \mathscr{H} \to 0.$$ Bó $\mathscr{G}$ là nội xạ nên flasque, suy ra $\mathscr{H}$ cũng là một bó flasque. 

Cố định một tập mở $U$. Ta sẽ chứng minh rằng $\text{H}^q(U,\mathscr{F}) = 0$ với mọi bó flasque $\mathscr{F}$ và mọi $q \ge 1$ bằng nhảy chiều (dimension shifting). Thật vậy, vì $\mathscr{G}$ là nội xạ nên $U$-acyclic, nói riêng, ta có $\text{H}^{q+1}(U,\mathscr{F}) = \text{H}^q(U,\mathscr{H})$ với mọi $q \ge 1$ (xem bài trước). Điều này cho phép ta thực hiện bước quy nạp. Ở bước $q = 1$, ta có $\text{H}^1(X,\mathscr{F}) = \text{Coker}(\mathscr{G}(U) \to \mathscr{H}(U)) = 0$ (vì $\mathscr{F}$ là flasque nên $\mathscr{G}(U) \to \mathscr{H}(U)$ là một toàn cấu). Điều này kết thúc chứng minh. $\square$

 

Cho $\mathscr{F}$ là một bó tùy ý trên $X$. Ta dùng xây dựng Godement để thu được dãy khớp $$0 \to \mathscr{F} \to C^0 \mathscr{F} \to C^1 \mathscr{F} \to \cdots,$$ trong đó mỗi bó $C^q \mathscr{F}$ đều flasque. Ở đây, $C^1 \mathscr{F} = C^0 \text{Coker}(\mathscr{F} \to C^0 \mathscr{F})$ và $C^{q+1} \mathscr{F} = C^0 \text{Coker}(C^{q-1}\mathscr{F} \to C^q \mathscr{F})$ với mọi $q \ge 1$. Nó được gọi là giải chính tắc Godement của $\mathscr{F}$. Với mỗi tập mở $U$, ta có $$\text{H}^q(U,\mathscr{F}) = \frac{\text{Ker}(C^q\mathscr{F}(U) \to C^{q+1}\mathscr{F}(U) )}{\text{Im}(C^{q-1}\mathscr{F}(U) \to C^{q}\mathscr{F}(U) )}, \qquad q \ge 1.$$ Về mặt lịch sử, đây là định nghĩa các nhóm đối đồng điều $\text{H}^q(U,\mathscr{F})$ mà Godement đã đưa ra.

 

Ví dụ. Cho $X$ là một đa tạp trơn. Với $q \ge 0$, ký hiệu $\Omega^q$ là bó các $q$-dạng vi phân trơn trên $X$ ($\Omega^0 = \mathcal{C}^\infty$. Các bó này flasque (sử dụng phân hoạch đơn vị!). Ta có một dãy khớp $$0 \to \underline{\mathbb{R}} \to \mathcal{C}^\infty \xrightarrow{d} \Omega^1 \xrightarrow{d} \Omega^2 \xrightarrow{d} \cdots,$$ trong đó $d: \Omega^q \to \Omega^{q+1}$ là phép đạo hàm ngoài (theo bổ đề Poincaré, và tính chất rằng mỗi điểm của $X$ đều một cơ sở lân cận gồm các tập mở hình sao). Áp dụng hàm tử lớp cắt toàn cục, ta thu được đối đồng điều de Rham $\text{H}^q_{\text{dR}}(X)$. Vì thế đối đồng điều de Rham đẳng cấu với đối đồng điều với hệ số trong bó hằng $\underline{\mathbb{R}}$, $$\text{H}^q_{\text{dR}}(X) = \text{H}^q(X, \underline{\mathbb{R}}), \qquad q \ge 0.$$

Tương tự, xét tiền bó $\text{C}_{\text{sing}}^q(-,\mathbb{R})$ các $q$-đối dây chuyền kỳ dị với hệ số thực, $q \ge 0$. Ta có một dãy khớp $$0 \to \underline{\mathbb{R}}^{\text{pre}} \to \text{C}_{\text{sing}}^0(-,\mathbb{R}) \xrightarrow{\delta} \text{C}_{\text{sing}}^1(-,\mathbb{R}) \xrightarrow{\delta} \cdots$$ các tiền bó trên $X$, trong đó $\delta$ là các đồng cấu đối biên (kiểm tra trên thớ, và lấy giới hạn trên cơ sở lân cận gồm các tập mở hình sao). Sau khi bó hóa, ta thu được một giải flasque khác của bó hằng $\underline{\mathbb{R}}$. Từ đó ta có chứng minh được (không dễ!) rằng đối đồng điều Betti cũng đẳng cấu với đồng điều với hệ số trong bó hằng, $$\text{H}^q(X,\underline{\mathbb{R}}) = \text{H}^q_{\text{sing}}(X,\mathbb{R}), \qquad q \ge 0.$$ Ta thu được định lý de Rham cổ điển (so sánh giữa đối đồng điều de Rham và đối đồng điều Betti)! 

File gửi kèm

•  9.png   7.38K   55 Số lần tải

Bài viết đã được chỉnh sửa nội dung bởi nmlinh16: 27-05-2021 - 13:36