GIỚI THIỆU
Định lý ba đường cao trong tam giác đồng quy được giới thiệu trong SGK toán 7 nhưng chỉ công nhận. Khi bắt đầu tìm cách chứng minh thì mình mới nhận ra là cũng không dễ chút nào.
Tại sao mình lại đi tìm tận 9 cách chứng minh? Chỉ là do trực giác mách bảo và thôi thúc vậy.
Mình tự giới hạn kiến thức vận dụng trong chương trình của lớp 6, 7, 8.
5 cách đầu tiên vận dụng tính chất hai tam giác đồng dạng. Bản thân mình thấy những cách này không hay lắm, nhưng vẫn đưa lên giới thiệu trước vì đó là cái mà mình nghĩ tới lúc ban đầu tìm tòi. Cách thứ 6, vận dụng tính chất trung tuyến ứng với cạnh huyền trong tam giác vuông. Ba cách còn lại vận dụng tính chất hình bình hành.
___________________
TÓM LƯỢC
Định lý: Ba đường cao trong một tam giác đồng quy.
Ta chỉ cần chứng minh định lý với trường hợp tam giác nhọn. Trường hợp tam giác vuông là hiển nhiên đúng, vì khi đó ba đường cao đồng quy ngay tại đỉnh góc vuông. Trường hợp tam giác tù, có thể suy ra trực tiếp từ trường hợp tam giác nhọn.
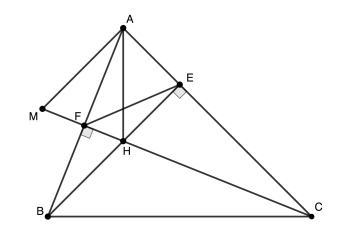
Xét tam giác ABC nhọn bất kỳ có hai đường cao BE và CF cắt nhau tại H. Để chứng minh ba đường cao của tam giác ABC đồng quy ta chứng minh một mệnh đề tương đương là AH vuông góc BC. Sau đây là các cách chứng minh mệnh đề này.
______________________
CÁCH 1. Đây là cách mình nghĩ ra đầu tiên và cũng là cách đơn giản nhất trong 9 cách, không cần vẽ thêm bất kì hình phụ nào. Nhưng mà giải xong mình cứ cảm thấy không thoả mãn do đó đã cất công tìm thêm những cách giải mới.
Ta có $\angle EBA=90^{\circ}-\angle BAC$ (vì tam giác BEA vuông tại E) và $\angle ECH=90^{\circ}-\angle BAC$ (vì tam giác CFA vuông tại F). Do đó $\angle EBA=\angle ECH.$
Ta lại có $\angle BEA=\angle CEH=90^{\circ}$ nên tam giác AEB đồng dạng với tam giác HEC (g.g).
Suy ra $\frac{EA}{EB}=\frac{EH}{EC}.$
Ta lại có $\angle AEH=\angle BEC=90^{\circ}$ nên tam giác AEH đồng dạng với tam giác BEC (c.g.c).
Do đó $\angle EAH=\angle EBC.$ Mặt khác $\angle EBC +\angle ACB=90^{\circ}$ (vì tam giác EBC vuông tại E). Suy ra $\angle EAH +\angle ECB=90^{\circ}.$
Vậy AH vuông góc với BC.
CÁCH 2.
Tam giác ECH và tam giác FCA đồng dạng vì có $\angle HEC=\angle AFC=90^{\circ}$ và góc C chung. Do đó $\frac{EC}{FC}=\frac{CH}{AC}.$
Suy ra tam giác ECF đồng dạng với tam giác HCA (c.g.c).
Vậy $\angle HAC=\angle EFH.$
Tam giác BHF và tam giác CHE đồng dạng vì có $\angle BFH=\angle CEH=90^{\circ}$ và có hai góc BHF và CHE đối đỉnh. Suy ra $\frac{HB}{HF}=\frac{HC}{HE}.$
Ta lại có EHF và BHC là hai góc đối đỉnh nên tam giác HEF đồng dạng với tam giác HCB (c.g.c).
Suy ra $\angle EFH=\angle EBC.$ Ta đã chứng minh ở trên $\angle HAC=\angle EFH$, cho nên $\angle HAC=\angle EBC.$
Mà $\angle EBC+\angle ACB=90^{\circ}$ (vì tam giác EBC vuông tại E). Do đó $\angle HAC +\angle ACB=90^{\circ}.$
Vậy AH vuông góc với BC.
CÁCH 3.
Qua A kẻ đường thẳng vuông góc với AC cắt tia CF tại M.
Ta có MA song song với BE vì cùng vuông góc AC. Theo định lý Ta-let ta có $\frac{MF}{FH}=\frac{AF}{FB}.$ Từ đó $\frac{MF}{MH}=\frac{AF}{AB}$, hay $\frac{MH}{AB}=\frac{MF}{AF}.$
Tam giác MAF đồng dạng với tam giác MCA vì có $\angle MFA=\angle MAC=90^{\circ}$ và góc M chung. Suy ra $\frac{MF}{AF}=\frac{MA}{AC}.$
Vậy $\frac{MH}{AB}=\frac{MA}{AC}.$
Ta lại có $\angle AMH=\angle BAC$ vì cùng phụ với góc MAB. Do đó tam giác MHA đồng dạng với tam giác ABC (c.g.c).
Suy ra $\angle AHM=\angle ABC.$ Mà $\angle AHM+\angle HAB=90^{\circ}$ nên $\angle ABC+\angle HAB=90^{\circ}.$
Vậy AH vuông góc BC.
CÁCH 4.
Qua A kẻ đường thẳng vuông góc với AH cắt các tia BE, CF lần lượt tại I và K.
Tam giác HEA đồng dạng với tam giác HAI (g.g) vì có $\angle AEH=\angle HAI =90^{\circ}$ và góc H chung. Suy ra $\frac{AH}{HI}=\frac{HE}{AH}$, hay $HE.HI=AH^2$. Tương tự ta có $HF.HK=AH^2$. Do đó $HE.HI=HF.HK$ hay $\frac{HE}{HF}=\frac{HK}{HI}.$Ta lại có tam giác HFB đồng dạng với tam giác HEC (g.g) vì có $\angle HFB=\angle HEC =90^{\circ}$ và cặp góc BHF, CHE đối đỉnh. Do đó $\frac{HE}{HF}=\frac {HC}{HB}.$
Vậy $\frac{HK}{HI}=\frac {HC}{HB}$. Theo định lý Talet đảo suy ra IK song song với BC. Mà AH vuông góc IK nên AH vuông góc với BC.
CÁCH 5.
Kẻ đường thẳng qua H vuông góc AH, cắt AC tại P. Ta có $\angle PHC=\angle BAH$ vì cùng phụ với $\angle AHF, \angle PCH=\angle ABH$ vì cùng phụ với $\angle BAC$. Do đó tam giác PCH đồng dạng với tam giác HBA (g.g). Suy ra $\frac{PC}{BH}= \frac{HP}{HA}.$ Ta lại có tam giác EHP đồng dạng với tam giác HAP (g.g) vì $\angle HEP=\angle AHP=90^{\circ}$ và góc P chung. Suy ra $\frac{PE}{HE}=\frac{HP}{HA}.$ Do đó $\frac{PC}{BH}=\frac{PE}{HE}$ hay $\frac{HE}{HB}=\frac{PE}{PC}.$ Theo định lý Talet đảo ta suy ra HP song song BC. Mà AH vuông góc HP nên AH vuông góc với BC.
CÁCH 6.
Gọi M là trung điểm BC, I là trung điểm AH. Tam giác AHE vuông tại E và AHF vuông tại F cùng có I là trung điểm của AH nên $IE=IF=\frac{AH}{2}.$ Tam giác BEC vuông tại E và BFC vuông tại F cùng có M là trung điểm BC nên $ME=MF=\frac{BC}{2}.$ Vậy $IE=EF$ và $ME=MF$, suy ra tam giác MEI bằng tam giác MFI.
Tam giác IHE cân tại I và MBE cân tại M nên
$\angle IEM=\angle IEH +\angle BEM=\angle IHE +\angle HBC.$
Tam giác IHF cân tại I và MCE cân tại M nên
$\angle IFM=\angle IFH +\angle BFM=\angle IHF +\angle HCB.$
Cộng vế với vế ta có
$\angle IEM+\angle IFM$
$=(\angle IHE + \angle IHF) + (\angle HBC +\angle HCB)$
$=\angle EHF + (180^{\circ} - \angle BHC) $
$=\angle EHF+ (180^{\circ} - \angle EHF)$
$=180^{\circ}.$
Mà $\angle IEM=\angle IFM$ vì hai tam giác MEI và MFI bằng nhau nên $\angle IEM=\angle IFM=90^{\circ}$.
Cuối cùng, để ý tam giác IAE cân tại E và tam giác MEC cân tại M ta có
$\angle HAC+\angle ACB= \angle IEA +\angle MEC=180^{\circ} - \angle IEM = 90^{\circ}.$
Vậy AH vuông góc BC.
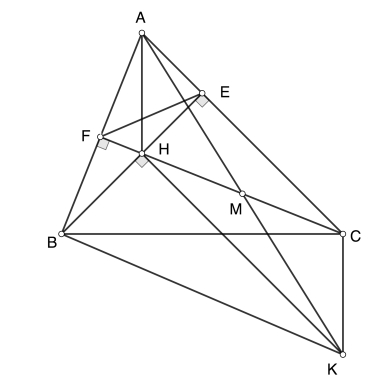
CÁCH 7.
Gọi M là trung điểm HC. K là điểm đối xứng với A qua M. Ta có ACKH là hình bình hành, suy ra AH song song CK và AC song song HK; $AC=HK$ và $AH=CK. $
Áp dụng định lý Pytago cho hai tam giác vuông BHF và AHF ta có
$BH^2=BF^2+HF^2$ và $AH^2=AF^2+HF^2. $
Trừ vế cho vế hai đẳng thức ta được $BH^2-AH^2=BF^2-AF^2. $Tương tự ta có $BC^2-AC^2=BF^2-AF^2. $
Do đó $BH^2-AH^2=BC^2-AC^2$ hay $BH^2+AC^2=AH^2+BC^2.$
Ta lại có $AC=HK$ và $AH=CK$ (cmt) nên
$BH^2+HK^2=CK^2+BC^2. $
Vì HK song song AC và BE vuông góc AC nên BE vuông góc HK. Tam giác BHK vuông tại H nên
$BK^2=BH^2+HK^2. $
Vậy $BK^2=CK^2+BC^2.$ Theo định lý Pytago đảo ta suy ra tam giác BCK vuông tại C, tức là CK vuông góc BC. Mà AH song song CK nên AH vuông góc BC.
CÁCH 8.
Gọi M là trung điểm BC, D đối xứng với H qua M và I là trung điểm AD.
Tứ giác BHCD là hình bình hành, mà $HB \bot AC$ và $HC \bot AB$ nên $BD \bot AB$ và $CD \bot AC.$
Tam giác ABD vuông tại B và tam giác ACD vuông tại C cùng có I là trung điểm AD nên $IB=IC.$
Tam giác IBC cân tại I và có M là trung điểm BC nên $IM \bot BC.$
Tam giác AHD có I là trung điểm AD và M là trung điểm HD nên AH song song IM. Vậy AH vuông góc BC.
CÁCH 9. Đây là cách với mình là đẹp nhất cũng là cách mà mình nghĩ ra sau cùng.
Qua A vẽ đường thẳng a song song với BC, qua B vẽ đường thẳng b song song với AC, qua C vẽ đường thẳng c song song với AB. Gọi A' là giao điểm của b và c, B' là giao điểm của a và c, C' là giao điểm của a và b.
Tứ giác ABCB' và ACBC' là các hình bình hành nên $AB'=AC'=BC$. Vậy A là trung điểm của B'C'. Tương tự ta có B là trung điểm A'C' và C là trung điểm A'B'.
Ta có $HB \bot AC$ và $A'C' \parallel AC$ nên $HB \bot A'C'.$ Mà B là trung điểm A'C' nên tam giác HA'C' cân tại H, do đó $HA'=HC'$. Tương tự ta có $HA'=HB'$. Suy ra $HB'=HC'$. Mà A là trung điểm của B'C' nên $AH \bot B'C'$. Ta lại có $B'C' \parallel BC$ nên AH vuông góc BC.
Bài viết đã được chỉnh sửa nội dung bởi HaiDangPham: 12-04-2023 - 21:09