Chủ đề này có 3 trả lời

[E. Galois]

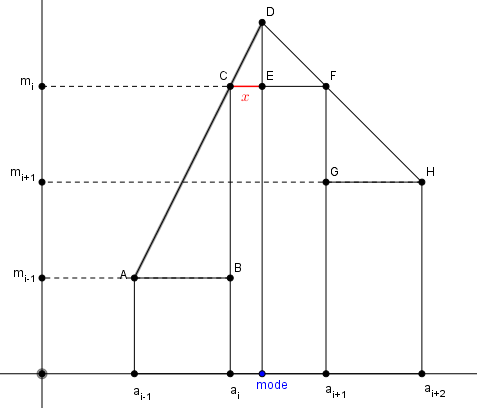
Ta biết rằng mode của mẫu dữ liệu là giá trị có tần số lớn nhất. Trong SGK toán 11 của chương trình giáo dục Phổ thông 2018 có công thức tính mode của mẫu dữ liệu ghép nhóm như sau:

 

Giả sử ta có bảng số liệu ghép nhóm sau

$$\begin{array}{|c|c|c|c|c|c|c|} \hline \text{Nhóm} & [a_1;a_2) & [a_2;a_3) & ... & [a_i;a_{i+1}) & ... & [a_{k-1};a_{k})  \\ \hline \text{Tần số} & m_1 &m_2  &...  &m_i  & ... & m_k \\ \hline \end{array}$$

Ở đây các nhóm có độ dài bằng nhau, tức là 

$$a_{i+1}-a_{i}=h, \quad i =1,...,k$$

Giả sử $[a_i; a_{i+1})$ là nhóm có tần số lớn nhất. Khi đó 

\begin{equation} \label{1} mode = a_i + \dfrac{m_i-m_{i-1}}{(m_i-m_{i-1})+(m_i-m_{i+1})}. h \end{equation}

Quy ước: $m_0=m_{k+1}=0$.

 

Mình không hiểu công thức $\eqref{1}$ có được từ đâu. Rất mong các bạn giúp mình chứng minh nó.

Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 14-10-2023 - 00:22

[E. Galois]

Cố gắng chứng minh công thức $\eqref{1}$ bằng hình học, ta thấy rằng, hợp lý nhất thì mode phải là hoành độ của giao điểm $D$ của $AC$ và $FH$. Đặt $x=CE$.

Ta có

$$\frac{x}{AB}=\frac{DE}{CB}\Rightarrow DE=\frac{x.CB}{AB}$$

$$\frac{EF}{GH}=\frac{DE}{FG}\Rightarrow DE=\frac{EF.FG}{GH}$$

Rõ ràng $AB=GH=h$, $EF=h-x$ nên ta có

$$\frac{x.CB}{h}=DE=\frac{(h-x).FG}{h}\Leftrightarrow x.(CB+FG)=h.FG \Leftrightarrow x= \frac{FG}{FG+CB}.h$$

Mà $FG=m_i-m_{i+1}$, $CB=m_i-m_{i-1}$. Do đó

$$x=\dfrac{m_i-m_{i+1}}{(m_i-m_{i-1})+(m_i-m_{i+1})}. h$$

Vậy 

$$\begin{equation} \label{2} mode = a_i + \dfrac{m_i-{\color{Red} m_{i+1}}}{(m_i-m_{i-1})+(m_i-m_{i+1})}. h \end{equation}$$

Công thức này không đúng so với $\eqref{1}$

 

Rất mong các bạn chỉ ra hộ mình chỗ chưa đúng.

Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 14-10-2023 - 00:31

[E. Galois]

Nếu coi mẫu dữ liệu là liên tục thì mode là điểm cực đại của hàm phân phối $F(x)$. Bài toán trở thành:
Cho hàm số $F(x)$ liên tục trên $[a_1;a_4]$. Chia đoạn $[a_1;a_4]$ thành ba đoạn bằng nhau $[a_1; a_2], [a_2; a_3]; [a_3; a_4]$. Đặt $$\sum_{x=a_i}^{a_{i+1}}F(x)=m_i, \quad i = 1,2,3.$$
Biết rằng $m_2>m_1; m_2>m_3$. Tìm điểm cực đại của $F(x)$.

Nhờ các bạn giải hộ bài toán này

Bài viết đã được chỉnh sửa nội dung bởi E. Galois: 14-10-2023 - 06:26

[nhungvienkimcuong]

Cố gắng chứng minh công thức $\eqref{1}$ bằng hình học, ta thấy rằng, hợp lý nhất thì mode phải là hoành độ của giao điểm $D$ của $AC$ và $FH$. Đặt $x=CE$.

screenshot_1697216271.png

Việc lấy giao điểm $AC\cap FH$ là chưa chính xác, vì điểm đạt được mode phải thỏa mãn "tỉ lệ". Như vậy để thu được kết quả đúng thì cần lấy giao điểm $BF\cap CG$.

 

Nếu coi mẫu dữ liệu là liên tục thì mode là điểm cực đại của hàm phân phối $F(x)$. Bài toán trở thành:
Cho hàm số $F(x)$ liên tục trên $[a_1;a_4]$. Chia đoạn $[a_1;a_4]$ thành ba đoạn bằng nhau $[a_1; a_2], [a_2; a_3]; [a_3; a_4]$. Đặt $$\sum_{x=a_i}^{a_{i+1}}F(x)=m_i, \quad i = 1,2,3.$$
Biết rằng $m_2>m_1; m_2>m_3$. Tìm điểm cực đại của $F(x)$.

Điểm cực đại sẽ là nghiệm của phương trình $F'(x)=0$.

Bài viết đã được chỉnh sửa nội dung bởi nhungvienkimcuong: 16-10-2023 - 06:36