Chủ đề này có 11 trả lời

[E. Galois]

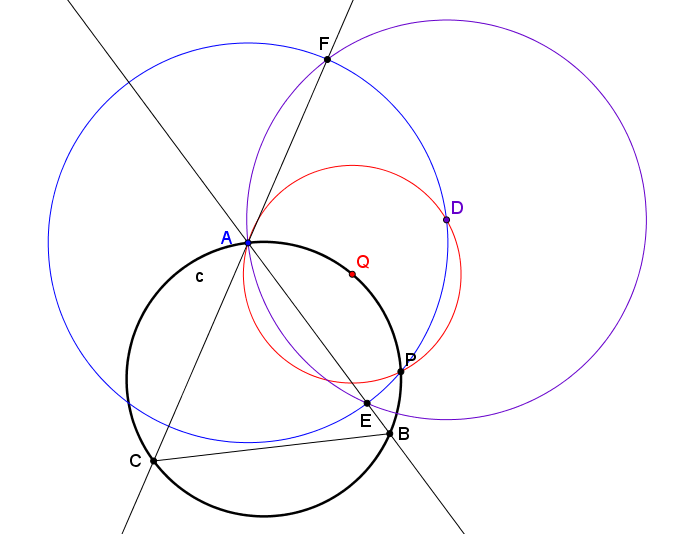
Cho điểm $A$ thuộc đường tròn $(c)$. Lấy điểm $Q \in (c)$, $Q$ bất kỳ khác $A$. Đường tròn $(Q,QA)$ cắt đường tròn  $(c)$ tại điểm thứ hai $P$. Đường tròn $(A,PA)$ cắt đường tròn  $(Q,QA)$ tại điểm thứ hai $D$. Đường tròn $(D,DA)$ cắt đường tròn  $(A, AP)$ tại $E,F$. Gọi $B,C$ là giao điểm thứ hai của $AE,AF$ với $(c)$. Chứng minh rằng $ABC$ là tam giác đều.

[VGNam]

sao e vẽ hình thử ko thấy nó đều là sao ạ? 

Bài viết đã được chỉnh sửa nội dung bởi VGNam: 17-02-2024 - 21:33

[E. Galois]

Tặng bạn cái hình

 

[VGNam]

e xin phép trình bày ngắn gọn lời giải của mình ạ:

Dễ thấy $AE= AF=AD= R_{A},DF=DA=DE=R_{D}\Rightarrow$ các tam giác $AFD, AED$ đều$\Rightarrow$$\angle CAB= 180^{\circ}-\angle EAD-\angle DAF=60^{\circ} $ $= \angle AED\Rightarrow AC$ song song $DE$

Gọi $K$=$DE\cap BC$

Đến đây chỉ việc chứng minh $\bigtriangleup EKB\sim \bigtriangleup DEA$ mà đã có góc E  đối đỉnh và các cặp cạnh tỉ lệ thì dùng thales là ra nên $\angle CBA= 60^{\circ}=\angle CAB$ $\Rightarrow \bigtriangleup ABC$đều.(đpcm)

Bài viết đã được chỉnh sửa nội dung bởi VGNam: 17-02-2024 - 23:40

[nguyenhuybao06]

e xin phép trình bày ngắn gọn lời giải của mình ạ:

Dễ thấy $AE= AF=AD= R_{A},DF=DA=DE=R_{D}\Rightarrow$ các tam giác $AFD, AED$ đều$\Rightarrow$$\angle CAB= 180^{\circ}-\angle EAD-\angle DAF=60^{\circ} $ $= \angle AED\Rightarrow AC$ song song $DE$

Gọi $K$=$DE\cap BC$

Đến đây chỉ việc chứng minh $\bigtriangleup EKB\sim \bigtriangleup DEA$ mà đã có góc E  đối đỉnh và các cặp cạnh tỉ lệ thì dùng thales là ra nên $\angle CBA= 60^{\circ}=\angle CAB$ $\Rightarrow \bigtriangleup ABC$đều.(đpcm)

Chỗ quan trọng nhất là cặp cạnh tỉ lệ để suy ra đồng dạng mà bạn lại không trình bày ra là sao nhỉ? 

[VGNam]

Chỗ quan trọng nhất là cặp cạnh tỉ lệ để suy ra đồng dạng mà bạn lại không trình bày ra là sao nhỉ? 

mình lm đến đây buồn ngủ díp mắt rồi nên nhảy luôn ấy   , có gì chắc mai mình bổ sung thêm

[VGNam]

Chỗ quan trọng nhất là cặp cạnh tỉ lệ để suy ra đồng dạng mà bạn lại không trình bày ra là sao nhỉ? 

Sáng nghĩ lại thấy  mình bị ngộ nhận bạn ạ! mình mặc định  BE=BK nên lúc đấy nghĩ dùng tỉ lệ nma cái kia đã chứng minh đc đâu 

Bây giờ thì bí r 

Bài viết đã được chỉnh sửa nội dung bởi VGNam: 18-02-2024 - 09:31

[hovutenha]

Dễ thấy $D$ thuộc tiếp tuyến tại $A$ của $(c)$. 

Có $(A,AP)$ cắt $(D,DA)$ tại $E,F$ và $AP=AD$ nên có ngay $\angle EAF = 120^{\circ}$ và $\angle EAD = \angle FAD = 60^{\circ}$

Suy ra $\angle B =\angle C = 60^{\circ}$ hay có $ABC$ là tam giác đều

[nguyenhuybao06]

Dễ thấy $D$ thuộc tiếp tuyến tại $A$ của $(c)$. 

Có $(A,AP)$ cắt $(D,DA)$ tại $E,F$ và $AP=AD$ nên có ngay $\angle EAF = 120^{\circ}$ và $\angle EAD = \angle FAD = 60^{\circ}$

Suy ra $\angle B =\angle C = 60^{\circ}$ hay có $ABC$ là tam giác đều

Bằng cách nào mà lại dễ thấy $D$ thuộc tiếp của $c$ tại $A$ vậy nhỉ? 

[MPU]

Vì $AD=AP \Leftrightarrow \widehat{AQP}=\widehat{AQD}$
Vì $AQ=PQ\Leftrightarrow \widehat{APQ}= \frac{180-\widehat{AQP}}{2}$
Vì $AQ=DQ\Leftrightarrow \widehat{DAQ}=\frac{180-\widehat{AQD}}{2}$
Do đó $\widehat{APQ}=\widehat{DAQ} \Rightarrow DA$ là tiếp tuyến tại $A$ của $(c)$.

[literallyme]

Cho điểm $A$ thuộc đường tròn $(c)$. Lấy điểm $Q \in (c)$, $Q$ bất kỳ khác $A$. Đường tròn $(Q,QA)$ cắt đường tròn  $(c)$ tại điểm thứ hai $P$. Đường tròn $(A,PA)$ cắt đường tròn  $(Q,QA)$ tại điểm thứ hai $D$. Đường tròn $(D,DA)$ cắt đường tròn  $(A, AP)$ tại $E,F$. Gọi $B,C$ là giao điểm thứ hai của $AE,AF$ với $(c)$. Chứng minh rằng $ABC$ là tam giác đều.

 

Mình chứng minh như sau (không phụ thuộc hình vẽ). Mình viết chứng minh dài vì giải thích từng tí một.

 

Hai đường tròn: đường tròn tâm $A$ với bán kính $AP$ và đường tròn tâm $D$ với bán kính $DA$ lần lượt đi qua tâm của nhau. Do đó với hai giao điểm $E$ và $F$ của chúng, chúng ta suy ra $AE = AF = DE = DF = AD$, kéo theo hai tam giác $ADE$ và $ADF$ là hai tam giác đều.

 

Tam giác $APD$ cân tại $A$ vì $P$ và $D$ cùng thuộc đường tròn tâm $A$ với bán kính $AP$. Cùng với việc $Q$ là tâm đường tròn ngoại tiếp tam giác $APD$, chúng ta chứng minh được hai tam giác $QDA$ và $QPA$ bằng nhau và cùng hướng. Từ điều này chúng ta có cặp góc bằng nhau, cụ thể là $(AQ, AD) \equiv (PQ, PA) \pmod{\pi}$. Nếu vẽ tiếp tuyến $t$ đi qua $A$ của đường tròn $c$ thì chúng ta có $(AQ, t) \equiv (PQ, PA) \pmod{\pi}$ (phiên bản góc định hướng cho định lý góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau). Do đó $(AQ, AD) \equiv (AQ, t)\pmod{\pi}$, điều này có nghĩa là $AD$ trùng $t$, hay $AD$ là tiếp tuyến tại $A$ của đường tròn $c$.

 

Tiếp tục áp dụng định lý về góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung, cùng với việc hai tam giác $ADE$ và $ADF$ đều (chúng cũng ngược hướng nữa) chúng ta có

$$(CA, CB)\equiv (AD, AB) \equiv (AD, AF) \equiv (FA, FD) \equiv -(FD, FA) \pmod{\pi}$$

$$(BA, BC)\equiv (AD, AC) \equiv (AD, AE) \equiv (AF, AD) \equiv -(AD, AF) \pmod{\pi}$$

Từ hai điều này, chúng ta suy ra hai tam giác $ABC$ và $DAF$ đồng dạng ngược hướng (trường hợp góc-góc). Vì tam giác $DAF$ là tam giác đều nên tam giác $ABC$ cũng là tam giác đều.

 

____

 

Lưu ý: Việc có $\angle EAF = 120^{\circ}$ là không đủ để suy ra $\angle BAC = 60^{\circ}$. Bởi vì nếu chỉ có $\angle EAF = 120^{\circ}$ thì $\angle BAC$ có thể có số đo là $60^{\circ}$ hoặc $120^{\circ}$.

 

Mình có góp ý nữa: Các bạn không nên dùng những từ như "dễ thấy" và "quen thuộc" vì đó là những tính từ mang tính chủ quan, làm suy giảm tính khách quan và sự dễ theo dõi cho người đọc. Ngoài ra, khi lập luận, nếu nêu rõ được dùng mệnh đề gì, điều kiện gì để "suy ra" thì tốt hơn là chỉ nêu mỗi "suy ra ..."

[perfectstrong]

Mình chứng minh như sau (không phụ thuộc hình vẽ). Mình viết chứng minh dài vì giải thích từng tí một.

 

Hai đường tròn: đường tròn tâm $A$ với bán kính $AP$ và đường tròn tâm $D$ với bán kính $DA$ lần lượt đi qua tâm của nhau. Do đó với hai giao điểm $E$ và $F$ của chúng, chúng ta suy ra $AE = AF = DE = DF = AD$, kéo theo hai tam giác $ADE$ và $ADF$ là hai tam giác đều.

 

Tam giác $APD$ cân tại $A$ vì $P$ và $D$ cùng thuộc đường tròn tâm $A$ với bán kính $AP$. Cùng với việc $Q$ là tâm đường tròn ngoại tiếp tam giác $APD$, chúng ta chứng minh được hai tam giác $QDA$ và $QPA$ bằng nhau và cùng hướng. Từ điều này chúng ta có cặp góc bằng nhau, cụ thể là $(AQ, AD) \equiv (PQ, PA) \pmod{\pi}$. Nếu vẽ tiếp tuyến $t$ đi qua $A$ của đường tròn $c$ thì chúng ta có $(AQ, t) \equiv (PQ, PA) \pmod{\pi}$ (phiên bản góc định hướng cho định lý góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung thì bằng nhau). Do đó $(AQ, AD) \equiv (AQ, t)\pmod{\pi}$, điều này có nghĩa là $AD$ trùng $t$, hay $AD$ là tiếp tuyến tại $A$ của đường tròn $c$.

 

Tiếp tục áp dụng định lý về góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung, cùng với việc hai tam giác $ADE$ và $ADF$ đều (chúng cũng ngược hướng nữa) chúng ta có

$$(CA, CB)\equiv (AD, AB) \equiv (AD, AF) \equiv (FA, FD) \equiv -(FD, FA) \pmod{\pi}$$

$$(BA, BC)\equiv (AD, AC) \equiv (AD, AE) \equiv (AF, AD) \equiv -(AD, AF) \pmod{\pi}$$

Từ hai điều này, chúng ta suy ra hai tam giác $ABC$ và $DAF$ đồng dạng ngược hướng (trường hợp góc-góc). Vì tam giác $DAF$ là tam giác đều nên tam giác $ABC$ cũng là tam giác đều.

 

____

 

Lưu ý: Việc có $\angle EAF = 120^{\circ}$ là không đủ để suy ra $\angle BAC = 60^{\circ}$. Bởi vì nếu chỉ có $\angle EAF = 120^{\circ}$ thì $\angle BAC$ có thể có số đo là $60^{\circ}$ hoặc $120^{\circ}$.

 

Mình có góp ý nữa: Các bạn không nên dùng những từ như "dễ thấy" và "quen thuộc" vì đó là những tính từ mang tính chủ quan, làm suy giảm tính khách quan và sự dễ theo dõi cho người đọc. Ngoài ra, khi lập luận, nếu nêu rõ được dùng mệnh đề gì, điều kiện gì để "suy ra" thì tốt hơn là chỉ nêu mỗi "suy ra ..."

Bạn dùng cả góc định hướng thì quá tầm THCS mất rồi Hình học THCS thì chỉ dừng lại ở mức trực quan chứ chưa thể làm chặt chẽ hơn như THPT Nhưng đúng là không nên "dễ thấy" và "quen thuộc", dễ tạo thành thói quen xấu khi đi kiểm tra thi thố.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 18-02-2024 - 11:16