Chủ đề này có 7 trả lời

[William Nguyen]

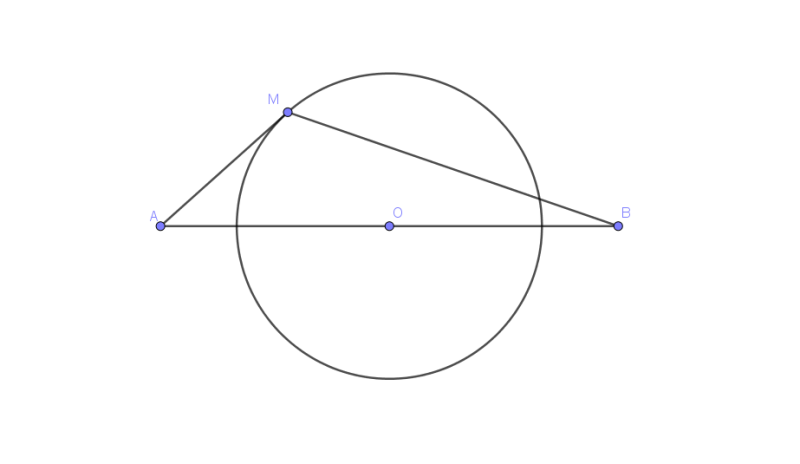
Trên mặt phẳng cho đường tròn tâm $O$, hai điểm $A$ và $B$ đối xứng nhau qua $O$ và nằm ngoài đường tròn $(O)$. Tìm vị trí các điểm $M$ trên đường tròn $(O)$ sao cho $P=MA+MB$ đạt GTLN, GTNN?

Hình gửi kèm

• 

[Leonguyen]

$\ast\quad MA+MB\ge AB,$ dấu bằng xảy ra khi $M$ nằm giữa $A$ và $B$ hay $M$ trùng với một trong hai giao điểm của $AB$ với $(O).$

$\ast\quad$Đặt $\angle MOA=\alpha.$

      Ta có \begin{align*}MA+MB&=\sqrt{OA^2+OM^2-2OA\cdot OM\cdot\cos\alpha}+\sqrt{OB^2+OM^2+2OB\cdot OM\cdot\cos\alpha}\\ &\le \sqrt{2(OA^2+OB^2+2OM^2)} =2\sqrt{OA^2+OM^2} \end{align*}

Dấu bằng xảy ra khi $\cos\alpha=0$ hay $M$ nằm chính giữa một trong hai nửa cung tròn tâm $(O)$ chia bởi $AB.$

Vậy $P$ đạt GTNN khi $M$ trùng với một trong hai giao điểm của $AB$ với $(O),$ $P$ đạt GTLN khi $M$ nằm chính giữa một trong hai nửa cung tròn tâm $(O)$ chia bởi $AB.$

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi Leonguyen: 24-04-2024 - 20:53

[perfectstrong]

Hãy thử tăng độ khó lên một chút : Tìm GTLN của $MA + MB$ khi $A, B$ đều nằm ngoài $(O)$ và $O$ nằm giữa $A,B$.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 24-04-2024 - 03:17

[William Nguyen]

Bài toán gốc:

 

Trường hợp GTNN thì dễ rồi

 

Trường hợp GTLN, mình trình bày cách làm khác bạn leonguyen một chút:

 

Khi $M$ không trùng một trong hai giao điểm của $AB$ với đường tròn tâm $O$, áp dụng công thức trung tuyến trong tam giác $ABM$:

 

$MO^2=\frac{MA^2+MB^2}{2} - \frac{AB^2}{4} \Rightarrow 4MO^2+AB^2=2(MA^2+MB^2) \geq (MA+MB)^2$

        $\Rightarrow P = MA+MB \leq \sqrt{4MO^2+AB^2}$ (không đổi)

 

Dấu "=" xảy ra khi và chỉ khi $M$ là giao của đường tròn tâm $O$ với đường trung trực đoạn $AB$.

 

Bài toán mở rộng của anh perfectstrong rất thú vị nhưng em chưa nghĩ ra, chúng ta cùng tiếp tục thảo luận nào.

[perfectstrong]

Khi đọc đề bài, mình nhớ tới một bài mà anh E. Galois đăng hồi lâu:

 

Cho hai điểm $A,B$ cùng nằm ở bên ngoài đường tròn $(O,r)$. Xác định vị trí điểm $M \in (O)$ sao cho $MA+MB $ nhỏ nhất

https://diendantoanh...o-mamb-nhỏ-nhất

 

Ở đây chỉ có bài toán tìm min với trường hợp tổng quát. Nhưng nếu suy nghĩ tìm max thì cũng sẽ rất thú vị

[Leonguyen]

* Tìm GTNN thì tương tự như bài gốc.

* Tìm GTLN

\begin{align*} MA+MB&=\sqrt{\frac{OA}{OB}}\sqrt{\frac{OB}{OA}(OA^2+OM^2-2OA\cdot OM\cdot\cos\alpha)}+\sqrt{OB^2+OM^2+2OB\cdot OM\cdot\cos\alpha}\\ &\le \sqrt{\left(\frac{OA}{OB}+1\right)\left(OA\cdot OB+\frac{OB}{OA}\cdot OM^2-2OB\cdot OM\cdot\cos\alpha+OB^2+OM^2+2OB\cdot OM\cdot\cos\alpha\right)}\\&=\sqrt{\left(\frac{OA}{OB}+1\right)\left(OA\cdot OB+\left(\frac{OB}{OA}+1\right)OM^2+OB^2\right)}\\&=\sqrt{AB^2+\left(\frac{OA}{OB}+\frac{OB}{OA}+2\right)OM^2} \end{align*}

Dấu bằng xảy ra khi

\begin{align*} &\frac{\frac{OB}{OA}(OA^2+OM^2-2OA\cdot OM\cdot\cos\alpha)}{\frac{OA}{OB}}=OB^2+OM^2+2OB\cdot OM\cdot\cos\alpha \\& \Leftrightarrow 1+ \frac{{O{M^2}}}{{O{A^2}}} - 2\frac{{OM}}{{OA}}\cos \alpha  = 1 + \frac{{O{M^2}}}{{O{B^2}}} + 2\frac{{OM}}{{OB}}\cos \alpha \\& \Leftrightarrow \frac{{O{M^2}}}{{O{A^2}}} - \frac{{O{M^2}}}{{O{B^2}}} = 2\frac{{OM}}{{OA}}\cos \alpha  + 2\frac{{OM}}{{OB}}\cos \alpha \\& \Leftrightarrow\cos\alpha=\frac{1}{2}OM\left( {\frac{1}{{OA}} - \frac{1}{{OB}}} \right) \end{align*}

Tình cờ phát hiện thêm nhưng chưa chứng minh được: Khi $M$ thoả mãn đẳng thức $\cos\alpha=\frac{1}{2}OM\left(\frac{1}{OA}-\frac{1}{OB}\right)$ thì $MO$ là đường phân giác $\bigtriangleup MAB.$

 

[William Nguyen]

Tình cờ phát hiện thêm nhưng chưa chứng minh được: Khi $M$ thoả mãn đẳng thức $\cos\alpha=\frac{1}{2}OM\left(\frac{1}{OA}-\frac{1}{OB}\right)$ thì $MO$ là đường phân giác $\bigtriangleup MAB.$

 

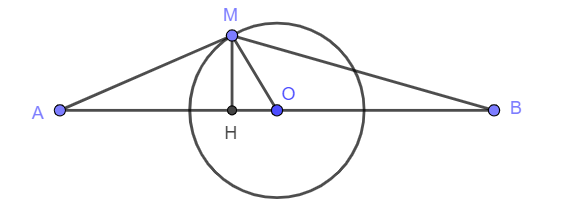
Mình chứng minh ý này như sau (trong TH OA<OB, với OA=OB là bài toán gốc và OA>OB tương tự):

 

Đường thẳng qua A song song MB cắt tia MO tại C. Gọi D là trung điểm MC thì ta có $\frac{OM}{OB}=\frac{ON}{OA}$ và $OM-ON=2OD$.

 

      $\cos\alpha=\frac{1}{2}OM\left(\frac{1}{OA}-\frac{1}{OB}\right)$

$\Leftrightarrow \cos\alpha=\frac{1}{2}.\left(\frac{OM}{OA}-\frac{ON}{OA} \right)$

$\Leftrightarrow \cos\alpha=\frac{OD}{OA}$

$\Leftrightarrow AD \perp MN$

$\Leftrightarrow \widehat{AMO}=\widehat{ANO}$

$\Leftrightarrow \widehat{AMO}=\widehat{BMO}$ hay $MO$ là phân giác góc $AMB$.

[perfectstrong]

Nhìn lời giải của các bạn thì có thể thấy rằng việc $A,B$ nằm ngoài $(O)$ không thật sự cần thiết. Chỉ cần $O$ nằm giữa $A,B$.

Như vậy, ta có thể thu gọn một chút mở rộng ở trên thành kết quả như sau:

Bài toán

Cho đường tròn $(O)$ và đoạn thẳng $AB$ chứa $O$. Một điểm $M$ chạy trên $(O)$. Chứng minh rằng $MA+MB$ đạt GTLN khi $MO$ là phân giác của $\widehat{AMB}$.

Nhìn hai bạn "song kiếm hợp bích" đẹp mắt quá. Giờ mà dừng lại thì thật uổng phải không?

Bài toán

Cho đường $(O)$ và 2 điểm $A,B$ sao cho $A,B,O$ thẳng hàng. Một điểm $M$ chạy trên $(O)$. Tìm GTLN của $MA+MB$?