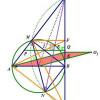
Bài 50: Cho đường tròn © và điểm I nằm trong đường tròn. Dựng qua I hai dây cung bất kỳ MIN, EIF. Gọi M’, N’, E’, F’ là các trung điểm của IM, IN, IE, IF.
a) Chứng minh rằng : tứ giác M’E’N’F’ là tứ giác nội tiếp.
b) Giả sử I thay đổi, các dây cung MIN, EIF thay đổi. Chứng minh rằng đường tròn ngoại tiếp tứ giác M’E’N’F’ có bán kính không đổi.
c) Giả sử I cố định, các day cung MIN, EIF thay đổi nhưng luôn vuông góc với nhau. Tìm vị trí của các dây cung MIN, EIF sao cho tứ giác M’E’N’F’ có diện tích lớn nhất.
----------------
a) Chứng minh rằng : tứ giác M’E’N’F’ là tứ giác nội tiếp.$\widehat{M'F'E'} = \widehat{MFE}$ (đường trung bình)
$\widehat{M'N'E'} = \widehat{MNE}$ (đường trung bình)
mà $\widehat{MFE} = \widehat{MNE}$ (cùng chắn cung ME)
$\Rightarrow$ tứ giác nội tiếp
b) Giả sử I thay đổi, các dây cung MIN, EIF thay đổi. Chứng minh rằng đường tròn ngoại tiếp tứ giác M’E’N’F’ có bán kính không đổi.Gọi J là tâm đường tròn ngoại tiếp tứ giác M’E’N’F’
$\Rightarrow$ $\Delta M'JF' \sim \Delta MOF$ (2 tam giác cân, có $\widehat{M'JF'} = 2\widehat{M'N'F'}$ , $\widehat{MOF} = 2\widehat{MNF}$)
$\Rightarrow$ $\frac{JF'}{OF} = \frac{M'F'}{MF} = \frac{1}{2}$
$\Rightarrow$ bán kính đường tròn J luôn không đổi
c) Giả sử I cố định, các dây cung MIN, EIF thay đổi nhưng luôn vuông góc với nhau. Tìm vị trí của các dây cung MIN, EIF sao cho tứ giác M’E’N’F’ có diện tích lớn nhất.$S_{M'E'N'F'} = \frac{1}{2}M'N'.E'F'=\frac{1}{2}\frac{MN.EF}{4}$
$\Rightarrow$ $S_{M'E'N'F'}max$ khi MN.EF max
Ta có $MN\leq 2R, EF\leq 2R$
$\Rightarrow$ $MN.EF\leq 4R^{2}$
Dấu "=" xảy ra khi MN và EF là 2 đường kính.
$\Rightarrow$ I trùng với O
Ps: câu c giải có vẻ không ổn lắm, có gì thiếu sót mọi người đóng góp ý kiến cho mình nhe.
Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 17-05-2012 - 09:23
