Chủ đề này có 10 trả lời

[Crystal]

Bài 1. Find all positive integers $ n\geq 2 $ such that for all integers $ i,j $ that $ 0\leq i,j\leq n $ and $ {n\choose i}+{n\choose j} $ have same parity.

Bài 2. Consider $ \omega $ is circumcircle of an acute triangle $ABC$. $D$ is midpoint of arc $ABC$ and $I$ is incenter of triangle $ABC$. Let $DI$ intersect $ABC$ in $E$ and $ \omega $ for second time in $F$. Let $P$ be a point on line $AF$ such that $PE$ is parallel to $AI$. Prove that $PE$ is bisector of angle $BPC$.

Bài 3. Let $n$ be a positive integer. Let $S$ be a subset of points on the plane with these conditions:

$i)$ There does not exist $n$ lines in the plane such that every element of $S$ be on at least one of them.

$ii)$ For all $ X\in S $ there exists $n$ lines in the plane such that every element of $ S-{X} $ be on at least one of them.

Find maximum of $ \mid S\mid $.

[E. Galois]

Bài 1. Tìm tất cả các số nguyên dương $ n\geq 2 $ sao cho với mọi số nguyên $ i,j $ sao cho $ 0\leq i,j\leq n $ and $ {n\choose i}+{n\choose j} $ có cùng tính chẵn lẻ.

Bài 2. Gọi $ \omega $ là đường tròn ngoại tiếp tam giácnhọn $ABC$. $D$ là điểm chính giữa cung $ABC$ và $I$ là tâm đường tròn nội tiếp tam giác $ABC$. Giả sử $DI$ giao với cung $ABC$ở $E$ và với đường tròn $ \omega $ tại điểm thứ hai $F$. Đặt $P$ là điểm trên $AF$ sao cho $PE$ song song với $AI$. Chứng minh rằng $PE$ là tia phân giác góc $BPC$.

Bài 3. Giả sử $n$ là một số nguyên dương . Gọi $S$ là tập hợp các điểm trong mặt phẳng thỏa mãn các tính chất sau:

$i)$ Không tồn tại $n$ đường thẳng nào trong mặt phẳng sao cho mọi điểm của $S$ nằm trên ít nhất 1 đường.

$ii)$ Với mọi $ X\in S $ tồn tại $n$ đường thẳng trong mặt phẳng sao cho mọi phần tử của $ S-{X} $ nằm trện ít nhất một đường trong số chúng

Tìm giá trị lớn nhất của $ \mid S\mid $.

[perfectstrong]

Cho mình hỏi bài 2. DI giao với cung ABC tại E thì E nằm đâu?
DI cắt $(\omega)$ tại 2 điểm D,F rồi.

[Karl Heinrich Marx]

Bài 1:
Viết $n$ trong hệ nhị phân như sau $a_1a_2...a_k$ trong đó $a_i \in {0;1}$ ta dễ thấy nếu $n$ thỏa đề bài thì các số $C_n^{i}$ là các số lẻ tức theo định lí Lucas thì với mọi $0 \le i \le n$ biếu diễn $i$ dưới dạng nhị phân $b_1b_2...b_k$ thì $b_i \le a_i$ như vậy ta phải luôn có $a_i=1$ nên $n=2^{k}-1$ là tất cả những số cần tìm

[perfectstrong]

Bài 2:
Vẽ AI cắt $(\omega)$ tại N. DN cắt BC tại M. NF cắt BC tại S.
AI là phân giác $\angle BAC$ nên NB=NC.
Kết hợp $DB=DC \Rightarrow$ DN là trung trực BC $\Rightarrow$ M là trung điểm BC và $\angle NME=90^o$

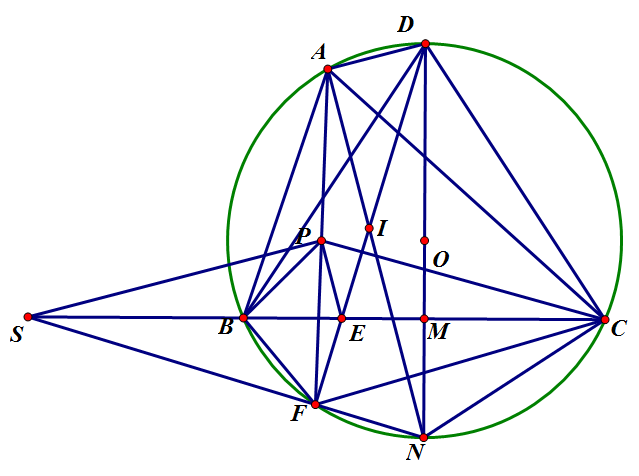
$OB=OC \Rightarrow O \in [DN] \Rightarrow \angle NFE=90^o$
$\Rightarrow$ NFEM là tgnt. Cùng BFNC là tgnt thì ta có
$\overline{SE}.\overline{SM}=\overline{SF}.\overline{SN}=\overline{SB}.\overline{SC}$
$\Rightarrow (SEBC)=-1$ (hệ thức Maclaurin)
$\Rightarrow P(SEBC)=-1$ (1)
Mặt khác $\angle FSE=\angle FAN=\angle FPE \Rightarrow$ SPEF là tgnt $\Rightarrow \angle SPE=180^o-\angle SFE=90^o$
$\Rightarrow PS \perp PE$ (2)
(1),(2) suy ra PE là phân giác góc hợp bởi PB,PC nên ta có đpcm.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 04-05-2012 - 14:59

[Cao Xuân Huy]

Bài 2. Gọi $ \omega $ là đường tròn ngoại tiếp tam giácnhọn $ABC$. $D$ là điểm chính giữa cung lớn $BC$ và $I$ là tâm đường tròn nội tiếp tam giác $ABC$. Giả sử $DI$ giao với $BC$ở $E$ và với đường tròn $ \omega $ tại điểm thứ hai $F$. Đặt $P$ là điểm trên $AF$ sao cho $PE$ song song với $AI$. Chứng minh rằng $PE$ là tia phân giác góc $BPC$.

Bài 2: Anh Hân đã giải nhưng em xin làm cách cấp 2

Theo em thấy ta không cần đến giả thiết $I$ là tâm đường tròn nội tiếp. Em nghĩ $I$ có thể là một điểm bất kì trên đoạn $AN$.

Gọi $M$ là trung điểm $BC$. $FN$ cắt $BC$ tại $S$ và $N$ là điểm chính giữa của cung nhỏ $BC$.

Ta có: $\widehat{FPE}=\widehat{FAN}=\widehat{FDN}$

Ta dễ dàng chứng minh rằng $\widehat{SMN}=\widehat{DFN}=90^o$. Do đó: $\widehat{FDN}=\widehat{FSM}$

Do đó: $\widehat{FPE}=\widehat{FSM}$

Suy ra: $SPEF$ là tứ giác nội tiếp. Do đó $\widehat{SPE}=180^o-\widehat{SFE}=90^o$.

Ta có: FE là phân giác $\widehat{BFC}$ và $SF\bot FE$ nên $SF$ là phân giác ngoài $\widehat{BFC}$.

Từ đó: $\frac{{SB}}{{SC}} = \frac{{BF}}{{FC}} = \frac{{BE}}{{EC}}$

Đặt: $\frac{{SB}}{{SC}} = \frac{{BE}}{{EC}} = k$

Lấy $H$ trên $PC$ sao cho $BH \bot PE$. $BH$ cắt $PE$ tại $G$

Ta có:
\[\frac{{BH}}{{SP}} = \frac{{BC}}{{SC}} = \frac{{SC - SB}}{{BC}} = 1 - k \Rightarrow BH = (1 - k).SP\]

Ta cũng có:
\[\frac{{SB}}{{SC}} = \frac{{BE}}{{EC}} = k \Rightarrow \frac{{SB}}{{BC}} = \frac{{SB}}{{SC - SB}} = \frac{k}{{1 - k}};\frac{{BE}}{{BC}} = \frac{{BE}}{{BE + EC}} = \frac{k}{{k + 1}}\]
\[ \Rightarrow \frac{{BE}}{{SB}} = \frac{{1 - k}}{{k + 1}} \Rightarrow \frac{{BG}}{{SP}} = \frac{{EB}}{{ES}} = \frac{{1 - k}}{2} = \frac{{BH}}{{2SP}} \Rightarrow BH = 2.BG\]

Do đó: $G$ là trung điểm $BH$ nên tam giác $PBH$ cân tại $P$.

Vậy $PE$ là phân giác của $\widehat{BPC}$

Bài viết đã được chỉnh sửa nội dung bởi Cao Xuân Huy: 07-05-2012 - 10:47

[perfectstrong]

Bài 2: Cách 3:
Vẽ PE kéo dài cắt OD tại K.
Dễ thấy DPFK,DBFC là tgnt nên
$\overline{EB}.\overline{EC}=\overline{EF}.\overline{ED}=\overline{EP}.\overline{EK}$
$\Rightarrow$ BPCK là tgnt. Mà KB=KC nên ta có đpcm.

[Crystal]

Day 2

Problem 1. Consider $m+1$ horizontal and $n+1$ vertical lines $(m,n \geqslant 4)$ in the plane forming an $ m\times n $ table. Cosider a closed path on the segments of this table such that it does not intersect itself and also it passes through all $ (m-1)(n-1) $ interior vertices (each vertex is an intersection point of two lines) and it doesn't pass through any of outer vertices. Suppose $A$ is the number of vertices such that the path passes through them straight forward, $B$ number of the table squares that only their two opposite sides are used in the path, and $C$ number of the table squares that none of their sides is used in the path. Prove that \[ A=B-C+m+n-1. \]
Problem 2.The function $ f:\mathbb{R}^{\ge 0}\longrightarrow\mathbb{R}^{\ge 0} $ satisfies the following properties for all $ a,b\in\mathbb{R}^{\ge 0} $:
a) $ f(a)=0\Leftrightarrow a=0 $
b) $ f(ab)=f(a)f(b) $
c) $ f(a+b)\le 2\max\{f(a),f(b)\} $
Prove that for all $ a,b\in\mathbb{R}^{\ge 0} $ we have $ f(a+b)\le f(a)+f(b) $.

Problem 3. The pentagon $ ABCDE $ is inscirbed in a circle $ w $. Suppose that $ w_{a},w_{b},w_{c},w_{d},w_{e} $ are reflections of $ w $ with respect to sides $ AB,BC,CD,DE,EA $ respectively. Let $ A' $ be the second intersection point of $ w_{a},w_{e} $ and define $ B',C',D',E' $ similarly. Prove that \[ 2\le\frac{S_{A'B'C'D'E'}}{S_{ABCDE}}\le 3, \]
where $ S_{X} $ denotes the surface of figure $X$.

[Crystal]

EXAM 2

Day 1

Problem 1.Is it possible to put $ \binom{n}{2} $ consecutive natural numbers on the edges of a complete graph with $n$ vertices in a way that for every path (or cycle) of length $3$ where the numbers $a,b$ and $c$ are written on its edges (edge $b$ is between edges $c$ and $a$), $b$ is divisible by the greatest common divisor of the numbers $a$ and $c$?

Problem 2.Let $ g(x) $ be a polynomial of degree at least $2$ with all of its coefficients positive. Find all functions $ f:\mathbb{R}^{+}\longrightarrow\mathbb{R}^{+} $ such that \[ f(f(x)+g(x)+2y)=f(x)+g(x)+2f(y)\quad\forall x,y\in\mathbb{R}^{+}. \]

----

Day 2

Problem 1.For positive reals $a,b$ and $c$ with $ab+bc+ca=1$, show that \[\sqrt 3 \left( {\sqrt a + \sqrt b + \sqrt c } \right) \leqslant \frac{{a\sqrt a }}{{bc}} + \frac{{b\sqrt b }}{{ca}} + \frac{{c\sqrt c }}{{ab}}.\]

Problem 2.Points $A$ and $B$ are on a circle $ \omega $ with center $O$ such that $ \frac{\pi}{3}<\angle AOB <\frac{2\pi}{3} $. Let $C$ be the circumcenter of the triangle $AOB$. Let $l$ be a line passing through $C$ such that the angle between $l$ and the segment $OC$ is $ \frac{\pi}{3} $. $l$ cuts tangents in $A$ and $B$ to $ \omega $ in $M$ and $N$ respectively. Suppose circumcircles of triangles $CAM$ and $CBN$, cut $ \omega $ again in $Q$ and $R$ respectively and theirselves in $P$ (other than $C$). Prove that $ OP\perp QR $.

Problem 3.We call a subset $B$ of natural numbers loyal if there exists natural numbers $ i\le j $ such that $ B=\{i,i+1,...,j\} $. Let $Q$ be the set of all loyal sets.

Now for every subset $ A=\{a_{1}<a_{2}<...<a_{k}\} $ of $ \{1,2,...,n\} $ we set $ f(A)=\max_{1\le i\le k-1}{a_{i+1}-a_{i}} $, and $ g(A)=\max_{B\subseteq A, B\in Q}|B| $. And we define $ F(n)=\sum_{A\subseteq\{1,2,...,n\}}f(A) $ and $ G(n)=\sum_{A\subseteq\{1,2,...,n\}}g(A) $.

Prove that there exists $ m\in\mathbb{N} $ such that for each natural number $n>m$, we have $ F(n)>G(n) $.

(By $ |A| $ we mean the number of elements of $A$ and if $ |A|\le 1 $, we define $ f(A) $ to be zero).

[Crystal]

EXAM 3

Problem 1. Consider a regular $ 2^{k} $-gon with center $O$ and label its sides clockwise by $ l_{1},l_{2},...,l_{2^{k}} $. Reflect $O$ with respect to $ l_{1} $, then reflect the resulting point with respect to $ l_{2} $ and do this process until the last side. Prove that the distance between the final point and $O$ is less than the perimeter of the $ 2^{k} $-gon.

Problem 2. Do there exist $2000$ real numbers (not necessarily distinct) such that all of them are not zero and if we put any group containing $1000$ of them as the roots of a monic polynomial of degree $1000$, the coefficients of the resulting polynomial (except the coefficient of $ x^{1000} $) be a permutation of the $1000$ remaining numbers?

Problem 3. Find all integer numbers $x$ and $y$ such that: \[ (y^{3}+xy-1)(x^{2}+x-y)=(x^{3}-xy+1)(y^{2}+x-y). \]

Theo AoPS

[Crystal]

Day 2

Problem 1. Suppose $p$ is an odd prime number. We call the polynomial $ f(x)=\sum_{j=0}^{n}a_{j}x^{j} $ with integer coefficients $i$-remainder if $ \sum_{p-1|j,j>0}a_{j}\equiv i\pmod{p} $. Prove that the set $ \{f(0),f(1),...,f(p-1)\} $ is a complete residue system modulo $p$ if and only if polynomials $ f(x), (f(x))^{2},...,(f(x))^{p-2} $ are $0$-remainder and the polynomial $ (f(x))^{p-1} $ is $1$-remainder.

Problem 2. Let $n$ be a natural number. Suppose $A$ and $B$ are two sets each containing $n$ points of plane such that no three points of a set are collinear. Let $ T(A) $ be the number of broken lines containing $n-1$ segments such that it doesn't intersect itself, and it's vertices are points of $A$. Define $ T(B) $ similarly. If points of $B$ are vertices of a convex $n$-gon but points of $A$ are not, prove that $ T(B)<T(A) $.

Problem 3. Let $O$ be the circumcenter of the acute triangle $ABC$. Suppose points $ A',B' $ and $ C' $ are on sides $ BC,CA $ and $AB$ such that circumcircles of triangles $ AB'C',BC'A' $ and $ CA'B' $ pass through $O$. Let $ l_{a} $ be the radical axis of the circle with center $ B' $ and radius $ B'C $ and circle with center $ C' $ and radius $ C'B $. Define $ l_{b} $ and $ l_{c} $ similarly. Prove that lines $ l_{a},l_{b} $ and $ l_{c} $ form a triangle such that it's orthocenter coincides with orthocenter of triangle $ ABC $.