Chủ đề này có 6 trả lời

[solitarycloud2612]

Trên phân giác góc A của $\vartriangle ABC$ lấy điểm M và N trong tam giác sao cho $\angle NBC = \angle MBA$
a)$cmr\angle NCB = \angle MCA$
b) Cmr đường tròn đi qua M, N và tiếp xúc với BC cũng tiếp xúc với đường tròn ngoại tiếp $\vartriangle ABC$

Bài viết đã được chỉnh sửa nội dung bởi solitarycloud2612: 25-05-2012 - 22:38

[Cao Xuân Huy]

Cao Xuân Huy: Câu a: http://diendantoanho...showtopic=72935

---

solitarycloud2612: Cần câu b kia!!

[solitarycloud2612]

Tham khảo thôi nhé, chỉ là ý thôi.
a) $cm\angle NCD = \angle MCA$
Kẻ BI là phân giác $\angle ABD(I \in AD)$, trên AD lấy M' sao cho $\angle NCD = \angle ACM'$
Ta có:$\frac{{AM}}
{{AN}} = \frac{{{S_{\vartriangle BAM}}}}
{{{S_{\vartriangle BDN}}}} = \frac{{\frac{1}
{2}BA.BM.\sin ABM}}
{{\frac{1}
{2}DB.BN.\sin ABM}} = \frac{{BA}}
{{BD}}.\frac{{BM}}
{{BN}} = \frac{{AI}}
{{ID}}.\frac{{MI}}
{{NI}}(1)$( do $\vartriangle BAM$ và $\vartriangle BDN$ có chung đường cao, $BI$ là phân giác)
Chứng minh tương tự với cách chứng minh trên ta có:

$\frac{{AM'}}
{{DN}} = \frac{{CA}}
{{CD}}.\frac{{CM'}}
{{CN}} = \frac{{AI}}
{{ID}}.\frac{{M'I}}
{{IN}}(2)$
Từ (1) và (2)$ \Rightarrow \frac{{AM}}
{{MI}} = \frac{{AM'}}
{{M'I}} \Rightarrow M \equiv M' \Rightarrow \angle NCD = \angle ACM$

[solitarycloud2612]

b) Cmr đường tròn đi qua M, N và tiếp xúc với BC cũng tiếp xúc với đường tròn ngoại tiếp $\vartriangle ABC$
+ Cách dựng hình:
- Quay đường tròn đường kính DM (N nằm giữa M, D)
- Hạ đường thẳng vuông góc với AD tại N cắt đường tròn đường kính DM tại I.
- Trên BC lấy J sao cho DJ=DI
- Đường vuông góc BC tại J cắt đường trung trực MN tại L$\Rightarrow $ Ta dựng được (L) đi qua M, N tiếp xúc với BC tại J và tiếp xúc với (O)
P/S: Cách dựng hình dựa vào bài toán phương tích.
Lời giải 1( cái này có chút gì ko ổn, mọi người tìm giùm)
Gỉa sử S là tiếp điểm giữa đường tròn tâm O ngoai tiếp$\vartriangle ABC$và (L), AD cắt (O) tại K, KS cắt BC tại J'.
Xét $\vartriangle KCJ'v{\text{\`a }}\vartriangle KSC$
có$\left\{ \begin{gathered}
\angle CKS = \angle CSJ' \\
\angle KSC = \angle J'CK \\
\end{gathered} \right.$

$\vartriangle KCJ' \sim \vartriangle KSC(g.g) \Rightarrow \frac{{KC}}
{{KJ'}} = \frac{{KS}}
{{KC}} \Rightarrow KJ'.KS = K{C^2}(1)$
xét $\vartriangle KCN$ và $\vartriangle KMC$
Có:$\left\{ \begin{gathered}
\angle K chung \\
\angle KCN = \angle KMC \\
\end{gathered} \right.$

$ \Rightarrow \vartriangle KCN \sim \vartriangle KMC(g.g) \Rightarrow \frac{{KC}}
{{KN}} = \frac{{KM}}
{{KC}} \Rightarrow KM.KN = K{C^2}(2)$
Từ (1) và (2) \Rightarrow MNJ'S là tứ giác nội tiếp
$\begin{gathered}
\Rightarrow J' \in (L) \\
\Rightarrow J' \equiv J \\
\end{gathered} $
Lời giải 2:
K là trung điểm cung nhỏ BC, J là tiếp điểm của (L) với BC. Nối KJ cắt (L) tại T
Chứng minh lại 2 cặp tam giác đồng dạng ở trên

$ \Rightarrow KJ.KT = KM.KN \Rightarrow \vartriangle KTC \sim \vartriangle KCJ \Rightarrow \angle KTC = \angle BCK = \angle KAC$
\Rightarrow T thuộc trên (O)
Lời giải 3: Cm${\text{OL = |OA - LN|}}$( bí)

[perfectstrong]

Anh nghĩ chắc em chép nhầm chỗ nào đó. Anh "ngâm cứu" ra như sau (dựa theo lời giải em đưa)
Lời giải 1:
Vẽ đường tròn $(L)$ qua $M,N$ tiếp xúc $BC$ tại $J$.
Vẽ đường tròn $(L')$ qua $M,N$ sao cho $L'$ và $L$ cùng phía so với $AD$, đồng thời, tiếp xúc trong với $(O)$ tại $S$.

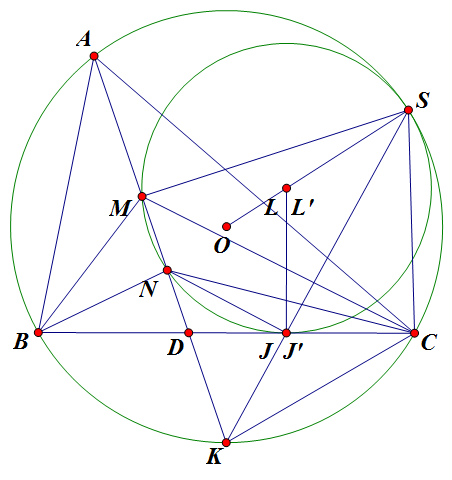
Ta sẽ chứng minh $(L) \equiv (L')$. Thật vậy
Vẽ $KS$ cắt $BC$ tại $J'$. Ta có:
$\angle KSC=\angle KCJ' \Rightarrow \vartriangle KSC \sim \vartriangle KCJ' (g.g) \Rightarrow KJ'.KS=KC^2 (1)$
$\angle KCN=\angle KCD+\angle NCD=\angle KAD+\angle ACM=\angle KAC+\angle ACM=\angle KMC$
$\Rightarrow \vartriangle KNC \sim \vartriangle KCN (g.g) \Rightarrow KM.KN=KC^2 (2)$
$(1),(2) \Rightarrow KM.KN=KJ'.KS \Rightarrow MNJ'S$ là tgnt.
$M,N,S \in (L') \Rightarrow J' \in (L')$.
Giờ ta sẽ chứng minh $(L')$ tiếp xúc $BC$ tại $J'$. Thật vậy, nếu $(L')$ cắt BC tại $X \neq J'$.
Vẽ $KX$ kéo dài, cắt $(L')$ tại $S' \Rightarrow KM.KN=KX.KS'=KC^2$
$\Rightarrow \vartriangle KS'C \sim \vartriangle KCX \Rightarrow \angle KS'C=\angle KCX=\angle KAC$
$\Rightarrow S' \in (O) \Rightarrow S' \equiv S \Rightarrow X \equiv J'$: trái điều giả sử.
Do đó, $(L')$ tiếp xúc $BC$ tại $J'$. Suy ra $(L) \equiv (L') \Rightarrow (L)$ tiếp xúc trong với $(O)$.
Lời giải 2:
Nó cũng giống lời giải 1, nhưng em thiếu 1 phần là phải chứng minh điểm T đó là duy nhất Anh viết lại cho đàng hoàng luôn.

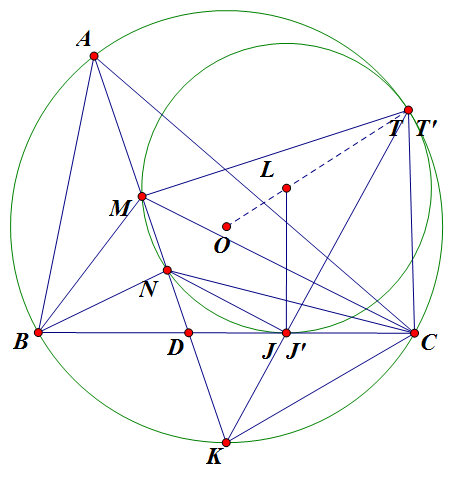
Vẽ $(L)$ tiếp xúc $BC$ tại $J$. Vẽ $KJ$ cắt $(L)$ tại $T$.
$\angle KCN=\angle KCD+\angle NCD=\angle KAD+\angle ACM=\angle KAC+\angle ACM=\angle KMC$
$\Rightarrow \vartriangle KNC \sim \vartriangle KCN (g.g)$
$\Rightarrow KC^2=KM.KN=KT.KJ \Rightarrow \vartriangle KCJ \sim \vartriangle KTC (c.g.c)$
$\Rightarrow \angle KTC=\angle KCJ=\angle KAC \Rightarrow T \in (O)$
Giả sử $(O)$ cắt $(L)$ tại $T' \neq T$. Vẽ $KT'$ cắt $BC$ tại $J'$.
$\vartriangle KT'C \sim \vartriangle KCJ' (g.g) \Rightarrow KJ'.KT'=KC^2=KM.KN$
$\Rightarrow J' \in (L) \Rightarrow (L)$ cắt $BC$ tại 2 điểm $J$ và $J'$: trái gt là $(L)$ tiếp xúc $BC$.
Do đó $(L)$ tiếp xúc trong với $(O)$.

Bài viết đã được chỉnh sửa nội dung bởi perfectstrong: 26-05-2012 - 20:52

[solitarycloud2612]

Lời giải 3 có thể áp dụng một phần nhỏ kiến thức 10 đó anh

[perfectstrong]

Lời giải 3 có thể áp dụng một phần nhỏ kiến thức 10 đó anh

Không hẳn 1 phần nhỏ đâu em mà phải là hầu hết kĩ năng trong hình học tọa độ lớp 10