Chủ đề này có 452 trả lời

[Beautifulsunrise]

Bài 62:
cho $\Delta ABC$ cân tại A , $\angle A=20^o$
Kẻ phân giác $\angle B $$ \cap$ Đường thẳng qua C //AB ={I}
Nối AI
Kẻ đường thẳng CE // AI $\cap AB$ ={E} .
Tính góc $\angle BEC$

Bài này chính là Bài 58: $\angle BEC = 30^0$

[chinhanh9]

Bài 64: Cho tam giác $ABC$ nội tiếp đường tròn $\left ( O;R \right )$. Vẽ $\left ( O_{1} \right )$ qua $A, B$ ; $\left ( O_{2} \right )$ qua $A,C$ . $\left ( O_{1} \right )$$,\left ( O_{2} \right )$ cắt nhau tại $D$, ($D$ khác $A$).Biết $\left ( O_{1} \right )$, $\left ( O_{2} \right )$ cùng tiếp xúc với $BC$.Tính bán kính đường tròn $BCD$.

 

BlackSelena: Đây là bài 60 mà anh =.=" 

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 23:00

[L Lawliet]

Đây là bài 60 mà anh =.="

Xóa bài đó hộ anh :|
Bài 63: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và ngoại tiếp đường tròn bán kính $r$. Gọi $O_1$, $R_1$; $O_2$, $R_2$; $O_3$, $R_3$ theo thứ tự là tâm và bán kính các đường tròn tiếp xúc với các cặp tia $AB$, $AC$; $BC$, $BA$; $CA$, $CB$ tương ứng. Chứng minh rằng:
$$R_1+R_2+R_3\geq 12r$$

[triethuynhmath]

Bài 64: Cho tam giác $ABC$ nội tiếp đường tròn $\left ( O;R \right )$. Vẽ $\left ( O_{1} \right )$ qua $A, B$ ; $\left ( O_{2} \right )$ qua $A,C$ . $\left ( O_{1} \right )$$,\left ( O_{2} \right )$ cắt nhau tại $D$, ($D$ khác $A$).Biết $\left ( O_{1} \right )$, $\left ( O_{2} \right )$ cùng tiếp xúc với $BC$.Tính bán kính đường tròn $BCD$.

Chắc ý bạn là tính đường tròn ngoại tiếp tam giác BCD.Nếu vậy thì mình xin chém:
Cho AD cắt (O) tại P.
Gọi I là tâm đường tròn ngoại tiếp tam giác BDC. Vẽ IJ vuông góc BC tại J => J là trung điểm $BC=> BJ=\frac{BC}{2}$.Từ giả thiết Ta có $O_{1}$ tiếp xúc BC tại B $\Rightarrow \angle DBC=\angle BAD=\angle BCP$ $=> BD//CP(SLT)$
Tương tự $\angle BCD=\angle DAC=\angle PBC \Rightarrow CD//BP$
=> BDCP là hình bình hành.
$\Rightarrow \angle BDC=\angle BPC=180^0-\angle A=$(Góc đối của hình bình hành và tgnt)
$\angle BCD=180^0-\angle A\Rightarrow \angle BIC=2(180^0-\angle BDC)=2(180^0-180^0+\angle A)=2\angle A$ .
Tam giác IBC cân tại I có IJ là đường cao nên đồng thời là phân giác => $\angle BIJ=\frac{\angle BIC}{2}=\frac{2\angle A}{2}=\angle A$
Ta có : Tam giác IJB vuông tại J => $\frac{BJ}{IB}=sin\angle BIJ\Rightarrow IB=\frac{BJ}{sinA}=\frac{BC}{2sinA}$ Vậy bán kính đường tròn ngoại tiếp tam giác BCD $=\frac{BC}{2sinA}(Q.E.D)$
Đây là hình vẽ bổ sung:

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 29-07-2012 - 19:27

[BlackSelena]

Bài 64: Cho tam giác $ABC$ nội tiếp đường tròn $\left ( O;R \right )$. Vẽ $\left ( O_{1} \right )$ qua $A, B$ ; $\left ( O_{2} \right )$ qua $A,C$ . $\left ( O_{1} \right )$$,\left ( O_{2} \right )$ cắt nhau tại $D$, ($D$ khác $A$).Biết $\left ( O_{1} \right )$, $\left ( O_{2} \right )$ cùng tiếp xúc với $BC$.Tính bán kính đường tròn $BCD$.

Cách khác ngắn hơn.
Từ $B$ kẻ đường thẳng $// CD$ cắt $(O)$ tại $E$.
Ta sẽ đi chứng minh $BECD:\text{ hình bình hành }$
Thật vậy, có
$\angle BDC = \angle BAD$
$\angle BCD = \angle CAD$
$\Rightarrow \angle BDC + \angle BCD = \angle BAC$
Mà $\angle BDC + \angle BCD = 180^o - \angle BDC$
$\Rightarrow \angle BDC + \angle BAC = 180^o$
Mặt khác, ta cũng có $ABEC: tgnt$
$\Rightarrow \angle BAC + \angle BEC = 180^o$
Vậy $\angle BEC + \angle BDC = 180^o$
$\Rightarrow \triangle BDC = \angle BEC$
$\Rightarrow BDCE: \text{ hình bình hành }$
Nhận thấy 2 tam giác bằng nhau thì bán kính đường tròn ngoại tiếp luôn bằng nhau
$\Rightarrow \text{ bán kính (I) } = R$
Ngắn hơn nhiều nhỉ

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 29-07-2012 - 20:03

[triethuynhmath]

Bài 65: Cho tam giác ABC.Một hình chữ nhật nội tiếp trong tam giác(M thuộc AB,N thuộc AC,P,Q thuộc BC).Chứng minh rằng tâm của hình chữ nhật MNPQ thuộc 1 đường cố định

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 29-07-2012 - 23:05

[Beautifulsunrise]

Bài 65: Cho tam giác ABC.Một hình chữ nhật nội tiếp trong tam giác(M thuộc AB,N thuộc AC,P,Q thuộc BC).Chứng minh rằng tâm của hình chữ nhật MNPQ thuộc 1 đường cố định

[tkvn97]

Bài 59 hiện vẫn chưa có lời giải

 

BlackSelena: bài đó khoai quá anh  . Cho em chút gợi ý cái.

Nếu ko ai giải đc thì anh post lời giải lên nhé 

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 23:01

[henry0905]

Bài 66: Cho $\triangle ABC$ có các phân giác trong AD,BE,CF cắt nhau tại Q. Tìm điều kiện $\triangle ABC$ để bán kính các đường tròn nội tiếp $\triangle AQF,BQD,CQE$ bằng nhau.

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 23:02

[BlackSelena]

Tiếp tục sê-ri về chùm bài tập tính góc
Bài 67: Cho $\triangle ABC$ cân tại $A$, $\angle A = 80^o$. Lấy điểm $E$ trên cạnh $AC$ và $D$ trên cạnh $BC$ sao cho $\angle ABE = 30^o$, $\angle CAD = 30^o$. Tính $\angle BED$
P/s: đây coi như là món ăn nhẹ trước những "ông lớn" như bài 66, 59

[hamdvk]

Bài 67: Cho $\triangle ABC$ cân tại $A$, $\angle A = 80^o$. Lấy điểm $E$ trên cạnh $AC$ và $D$ trên cạnh $BC$ sao cho $\angle ABE = 30^o$, $\angle CAD = 30^o$. Tính $\angle BED$

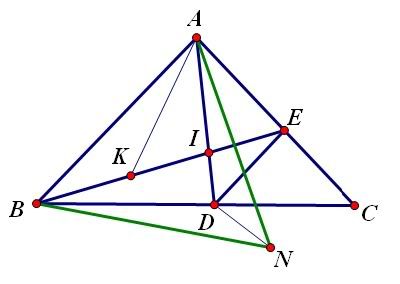
Vẽ tam giác đều ABN (N thuộc nửa mặt phẳng bờ AB chứa C)
Dễ cm D nằm trong $\Delta ABN$
Lấy K thuộc BE sao cho $\widehat{KAI}=40^{\circ}$
Mà $\widehat{KIA}=180^{\circ}-\widehat{ABE}-\widehat{BAI}=100^{\circ}$$\Rightarrow \widehat{KAI}=\widehat{IKA}=40^{\circ}$
$\Rightarrow \Delta AKI$ cân tại I => KI=IA
Xét $\Delta AKE$ có $\widehat{KAE}=\widehat{KEA}=70^{\circ}$ $\Rightarrow \Delta AKE$ cân tại K => KE=KA
Ta có $\Delta DBN=\Delta DAN (c.g.c)$
$\Rightarrow \widehat{BND}=\widehat{AND}=30^{\circ}$
$\Rightarrow \Delta KAB=\Delta DBN (g.c.g)=\Delta DAN$ $\Rightarrow AK=AD$ mà $AK=KE$$\Rightarrow KE=AD$
mà KI=AI $\Rightarrow IE=ID$
$\Rightarrow \Delta IDE$ cân tại I có $\widehat{DIE}=100^{\circ}$ $\Rightarrow \widehat{BED}=40^{\circ}$

[hamdvk]

Bài 68 . Cho $\Delta ABC$ có $\widehat{B}=\widehat{C}=50^{\circ}$. N thuộc miền trong tam giác thoả mãn $\widehat{NBC}=10^{\circ};\widehat{NCB}=20^{\circ}$. Tính $\widehat{ANB}$
--------------
!!!!!!!!!!!
-------------

[BlackSelena]

Bài 68 . Cho $\Delta ABC$ có $\widehat{B}=\widehat{C}=50^{\circ}$. N thuộc miền trong tam giác thoả mãn $\widehat{NBC}=10^{\circ};\widehat{NCB}=20^{\circ}$. Tính $\widehat{ANB}$
--------------
!!!!!!!!!!!
-------------

Lời giải bài 68:
Trên tia đối của $AC$ lấy điểm $E$ sao cho $EC = BC$.
Dễ dàng chứng minh $\triangle ENB:\text{ đều }$
Dễ thấy $\angle ABN = 30^o$
$\Rightarrow \angle EBA = 60^0 - 30^o= 30^o$
$\Rightarrow AB$ là trung trực của $EN$
$\Rightarrow \angle ANE = \angle AEN = 20^o$
$\Rightarrow \angle ANB =\angle AEN + \angle ENB = 20^o + 60^o = 80^o$
___________
Hình như đêm hôm qua có làm bài này rồi @@!

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 30-07-2012 - 17:23

[Karl Vierstein]

Bài 63: Cho tam giác $ABC$ nội tiếp đường tròn $(O)$ và ngoại tiếp đường tròn bán kính $r$. Gọi $O_1$, $R_1$; $O_2$, $R_2$; $O_3$, $R_3$ theo thứ tự là tâm và bán kính các đường tròn tiếp xúc với các cặp tia $AB$, $AC$; $BC$, $BA$; $CA$, $CB$ tương ứng. Chứng minh rằng:
$$R_1+R_2+R_3\geq 12r$$

Giải:
Giả sử đường tròn $(O_1)$ bán kính $R_1$ tiếp xúc ngoài với đường tròn $(O)$ bán kính $R$ ở $D$ và tiếp xúc với hai tia $AB$, $AC$ ở $M$ và $N$. Tia $AD$ cắt đường tròn $(O_1)$ ở $E$, như vậy ta có:
$OO_1=OD+DO_1=R+R_1$, $OA\parallel O_1E$ và $AM^2=AN^2=AD.AE$.
Do đó:
$\frac{AD^2}{AM^2}=\frac{AD}{AE}=\frac{OD}{OO_1}$ hay là $\frac{AD^2}{AM^2}=\frac{R}{R+R_1}$
Từ đó suy ra:
Chứng minh tương tự ta được:
$\frac{BD^2}{BM^2}=\frac{CD^2}{CN^2}=\frac{R}{R+R_1}$
Từ đó suy ra:
$\frac{AD}{AM}=\frac{BD}{BM}=\frac{CD}{CN}$ $(1)$
Mặt khác, tứ giác lồi $ABDC$ nội tiếp đường tròn $(O)$ nên theo định lý $Ptolemy$ ta có:
$AB.CD+CA.BD=BC.AD$ $(2)$
Từ $(1)$ và $(2)$ ta được:
$AB.CN+CA.BM=BC.AM$ $(3)$
Đặt $BC=a$, $CA=b$, $AB=c$ thay $BM=AM-c$ và $CN=AN-b=AM-b$ vào $(3)$ ta được:
$AM=AN=\frac{2bc}{b+c-a}$ $(4)$
Gọi $L$ là tiếp điểm của $AB$ với đường tròn tâm $I$ nội tiếp tam giác $ABC$, ta được $\frac{O_1M}{IL}=\frac{AM}{AL}$ hay là $\frac{R_1}{r}=\frac{AM}{AL}$.
Thay $AL=p-a=\frac{1}{2}\left ( b+c-a \right )$ và $AM$ bởi $(4)$, ta được:
$\frac{R_1}{r}=\frac{4bc}{\left ( a+b-c \right )^2}$
Chứng minh tương tự, ta được:
$\frac{R_2}{r}=\frac{4ca}{\left ( c+a-b \right )^2}$ và $\frac{R_3}{r}=\frac{4ab}{\left ( a+b-c \right )^2}$ $(5)$
Từ các hệ thức $(5)$ và theo bất đẳng thức $AM-GM$, ta được:
$\frac{R_1+R_2+R_3}{r}=\frac{bc}{\left ( b+c-a \right )^2}+\frac{ca}{\left ( c+a-b \right )^2}+\frac{ab}{\left ( a+b-c \right )^2}\geq \sqrt[3]{\frac{a^2b^2c^2}{\left ( b+c-a \right )^2\left ( c+a-b \right )^2\left ( a+b-c \right )^2}}$ $(6)$
Vì $a$, $b$, $c$ là độ dài các cạnh của một tam giác nên ta có bất đẳng thức:
$\left ( b+c-a \right )\left ( c+a-b \right )\left ( c+a-b \right )\leq abc$ $(7)$
(Bất đẳng thức này dễ dàng chứng minh!)
Từ $(6)$ và $(7)$ ta thu được:
$R_1+R_2+R_3\geq 12r$
Đẳng thức xảy ra khi và chỉ khi:
$R_1=R_2=R_3$ và $b+c-a=c+a-b=a+b-c$ do đó khi và chỉ khi tam giác $ABC$ là tam giác đều.
Hình mình đang vẽ up sau nhé chủ topic.

[Tru09]

Lời giải bài 68:
Trên tia đối của $AC$ lấy điểm $E$ sao cho $EC = BC$.
Dễ dàng chứng minh $\triangle ENB:\text{ đều }$
Dễ thấy $\angle ABN = 30^o$
$\Rightarrow \angle EBA = 60^0 - 30^o= 30^o$
$\Rightarrow AB$ là trung trực của $EN$
$\Rightarrow \angle ANE = \angle AEN = 10^o$
$\Rightarrow \angle ANB =\angle AEN + \angle ENB = 10^o + 60^o = 70^o$
___________
Hình như đêm hôm qua có làm bài này rồi @@!

Có vẻ sai rồi bạn àk
Lệnh 0,01 thì có vẻ không ảnh hưởng đến cả 10 độ nhỉ ??
Nhầm J với N
_________

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 30-07-2012 - 17:23

[L Lawliet]

Bài 69: Cho nữa đường tròn đường kính $AB$, bán kính $R$. Lấy điểm $C$ trên nữa đường tròn ($C$ khác $A$, $C$ khác $B$). Hạ $CH$ vuông góc với $AB$. Gọi $O_1$, $O_2$ theo thứ tự là tâm đường tròn nội tiếp tam giác $AHC$, $BHC$. Tìm vị trí của điểm $C$ để $O_1O_2$ có $GTLN$ và tính giá trị đó theo $R$.

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 31-07-2012 - 14:22

[Beautifulsunrise]

Bài 70 (Lớp 7). Cho tam giác ABC có $\widehat{A}=30^0$, H là trực tâm, M là trung điểm cạnh BC. Trên tia đối của tia MH lấy điểm T sao cho MH = MT. CMR: AT = 2BC.

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 30-07-2012 - 23:15

[BlackSelena]

Mất cả đêm để nghĩ bài 69, em buồn ngủ lắm rồi nên viết tạm cái hướng. Sáng mai đi học về viết tiếp
Kéo dài $O_1O_2$ cắt $CA,CB$ lần lượt tại $P,Q$.
Khi đó ta cần chứng minh $CP=CH=CQ$ (Đã chứng minh).
Vậy $O_1O_2 = PQ - PO_1 - QO_2$, ta cần đi tìm max cái này.
Không mất tính tq, giả sử $AH \geq BH$
$(O_1)$ tiếp xúc $CA$ tại $T$, khi đó có $PO_1=\sqrt{2}PT = \frac{AH+CH-AC}{\sqrt{2}}$
Tương tự ta có $QO_2 = \frac{CH+BH-BC}{\sqrt{2}}$
Vậy tổng hai thằng cha này max khi $C$ nằm chính giữa cung $BC$.
Khi đó ta đã có $CQ,CP$ max.
NGỦ THÔI !!!
_________________
Bổ sung thêm phần chứng minh vuông cân của chú binhmetric giúp mình

Viết chi tiết hơn
$QO_2 + PO_1 = \frac{AH+CH-AC+CH+BH-BC}{\sqrt{2}}$
$- (AC + BC) \leq 2\sqrt{AB.BC} = 2\sqrt{CH.AB}$
Vậy biểu thức này min khi $C$ nằm chính giữa cung $AB$
Mặt khác để tổng AB+ 2CH max thì cũng có $C$ nằm chính giữa cung $AB$.
Vậy ta tìm được min biểu thức $QO_2 + PO_1$
Mà max biểu $PQ$ khi $CP$ và $CQ$ max tức $CH$ max tức $C$ nằm chính giữa cung $AB$.
Vậy ta đã tìm được vị trí của $C$ để $O_1O_2$ max.
Còn phần tính toán thì làm như anh Karl là rất hay rồi .
_________________
P/s: cách siêu dài + siđa, nhưng đây là do tự mình nghĩ ra nên cảm thấy rất vui .

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 31-07-2012 - 11:35

[Karl Vierstein]

Bài 69: Cho nữa đường tròn đường kính $AB$, bán kính $R$. Lấy điểm $C$ trên nữa đường tròn ($C$ khác $A$, $C$ khác $B$). Hạ $CH$ vuông góc với $AB$. Gọi $O_1$, $O_2$ theo thứ tự là tâm đường tròn nội tiếp tam giác $AHC$, $BHC$. Tìm vị trí của điểm $C$ để $O_1O_2$ có $GTLN$ và tính giá trị đó theo $R$.

Giải:

Gọi $I$ là tâm đường tròn nội tiếp tam giác $ABC$ và $E$ là giao điểm của tia $CO_1$ với $AB$.
Ta có:
$\widehat{CEB}=\widehat{A}+\widehat{ACE}=\widehat{HCB}+\widehat{HCE}=\widehat{ECB}$
Suy ra tam giác $CBE$ cân tại $B$. Mà $BO_2$ là phân giác trong của $\widehat{EBC}$ nên $BO_2\perp CO_1$. Chứng minh tương tự ta được $AO_1\perp CO_2$.
Suy ra $I$ là trực tâm của tam giác $CO_1O_2$.
Gọi $K$ là giao điểm của tia $BO_2$ với $EC$ thì ta có: $\widehat{O_2KC}=45^o$ (vì $CO_1$, $CO_2$ là các tia phân giác của hai góc kề phụ nhau) nên tam giác $CO_2K$ vuông cân và ta có $KC=KO_2$.
Suy ra $\Delta CKI=\Delta O_2KO_1$ $(g.c.g)$ và do đó $O_1O_2=CI$.
Như vậy bài toán trở thành tìm vị trí của $C$ sao cho $CI$ có $GTLN$.
Gọi $D$ là giao điểm của tia $CI$ với cung $AB$ (đối xứng với cung $ACB$ qua $AB$), do $CI$ là đường phân giác của góc $BCA$ nên $D$ là điểm chính giữa cung này.
Ta có:
$\widehat{DAI}=\widehat{DAB}+\widehat{BAI}=\widehat{DCB}+\widehat{CAI}=\widehat{ICA}+\widehat{CAI}=\widehat{DIA}$
Suy ra tam giác $IDA$ cân tại $D$, do đó $DI=DA$ không đổi.
Như vậy, $CI=CD-DI=CD-DA$, mà $DA$ không đổi nên $CI$ đạt $GTLN$ khi và chỉ khi $CD$ có $GTLN$, tức là bằng $2R$ (quan hệ giữa đường kính và dây) hay $C$ là điểm chính giữa cung $AB$ đã cho.
Khi đó:
$O_1O_2=CI=2R-R\sqrt{2}=R\left ( 2-\sqrt{2} \right )$.
----
@BlackSelena: Có gì bạn pm qua tin nhắn riêng của mình nhé, sửa bài của mình mình không đọc được đâu!

Bài viết đã được chỉnh sửa nội dung bởi Karl Vierstein: 31-07-2012 - 13:52

[tkvn97]

Bài 71 .
Cho tam giác ABC có diện tích S . Các điểm D , E , F theo thứ tự nằm trên các cạnh AB , BC , CA sao cho AD = BD , $BE=\frac{1}{2}EC$ , $CF=\frac{1}{3}FA$. Các đoạn thẳng AE , BF , CD cắt nhau tạo thành một tam giác . Tính diện tích tam giác đó .
Bài 72. Cho tam giác đều ABC, các điểm D , E theo thứ tự thuộc các cạnh AC , AB sao cho BD , CE cắt nhau tại P và diện tích tứ giác ADPE bằng diện tích tam giác BPC . Tính $\widehat{BPE}$
_____________________
@BlackSelena: em mong anh hãy cung cấp lời giải bài 59 trước khi post bài mới để tránh loãng topic

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 31-07-2012 - 12:26