Chủ đề này có 452 trả lời

[triethuynhmath]

Bài 77(Số đẹp):
Cho tam giác ABC nhọn,3 đường cao AD,BE,CF cắt nhau tại H.Gọi M là trung điểm BC,EF cắt BC tại N.Gọi (M) là đường tròn đường kính BC , cho AD cắt (M) tại K.CMR: NK là tiếp tuyến của (M).
P/s: Bài này trông đơn giản mà thật ra lại khá hay,hiện tại mình mới chỉ sở hữu được 2 cách,các bạn ráng mở rộng và tìm thêm các lời giải mới nhé,khuyến khích đăng nhiều cách .

[henry0905]

Bài 77(Số đẹp):
Cho tam giác ABC nhọn,3 đường cao AD,BE,CF cắt nhau tại H.Gọi M là trung điểm BC,EF cắt BC tại N.Gọi (M) là đường tròn đường kính BC , cho AD cắt (M) tại K.CMR: NK là tiếp tuyến của (M).
P/s: Bài này trông đơn giản mà thật ra lại khá hay,hiện tại mình mới chỉ sở hữu được 2 cách,các bạn ráng mở rộng và tìm thêm các lời giải mới nhé,khuyến khích đăng nhiều cách .

Giải cách đơn giản nhất vậy
Ta có $\triangle MFE$ cân
$\Rightarrow 2\widehat{FEM}=180^{\circ}-\widehat{FME}$
$\Rightarrow \widehat{FEM}=90^{\circ}-\widehat{FBE}=\widehat{FHB}=\widehat{EDC}$
$\Rightarrow KM^{2}=ME^{2}=MD.MN$
$\Rightarrow$ NK vuông góc KM

Bài viết đã được chỉnh sửa nội dung bởi henry0905: 02-08-2012 - 23:03

[Beautifulsunrise]

Bài 77(Số đẹp):
Cho tam giác ABC nhọn,3 đường cao AD,BE,CF cắt nhau tại H.Gọi M là trung điểm BC,EF cắt BC tại N.Gọi (M) là đường tròn đường kính BC , cho AD cắt (M) tại K.CMR: NK là tiếp tuyến của (M).
P/s: Bài này trông đơn giản mà thật ra lại khá hay,hiện tại mình mới chỉ sở hữu được 2 cách,các bạn ráng mở rộng và tìm thêm các lời giải mới nhé,khuyến khích đăng nhiều cách .

-------------------------------------------
P/S: Nhận thấy chỉ cần AD là đường cao và AD, BE, CF đồng quy là đủ để NK là tiếp tuyến (M) mà không cần phải có BE, CF là đường cao. @_^

Bài viết đã được chỉnh sửa nội dung bởi binhmetric: 02-08-2012 - 23:09

[Tru09]

Bài 78:
Cho $\Delta ABC$ có G là trọng tâm ,3 cạnh :a,b,c .Một điểm M bất kỳ.Đoạn thẳng MG =d
Tính $MA^2 +MB^2 +MC^2$ theo a,b,c,d
----------------------------------------
Ai làm nốt bài 44 di

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 23:09

[BlackSelena]

Bài 76. Cho tam giác ABC cân tại B và P nằm trong tam giác, biết $\angle ABC = {80^0},\angle PAC = {40^0},\angle PCA = {30^0}$. Tìm $\angle BPC$

Bỏ luôn cách sin cos phức tạp kia đi =;.
Lời giải bài 76

Trên $CP$ lấy điểm $E$ sao cho $\triangle AEC:\text{cân}$.
Dễ thấy $\angle BAP = 10^o = \angle EAP$
$\Rightarrow AP$ là phân giác của $\angle BAE$.
Mặt khác, cũng dễ thấy $\angle BEP = \angle CEP = 60^o$
$\Rightarrow EP$ là phân giác $\angle BEA$
$\Rightarrow P$ là tâm đường tròn ngoại tiếp $\triangle ABE$
$\Rightarrow BP$ là phân giác $\angle ABE$
Mặt khác $\triangle ABE = \triangle CBE$
$\Rightarrow \angle ABE = \angle CBE = 40^o$
$\Rightarrow \angle ABP = 20^o$
$\Rightarrow \angle BPA = 150^o$
Mà ta lại có $\angle APC = 110^o$
$\Rightarrow \angle BPC = 360^o - 150^o - 110^o = 100^o$

 

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 23:09

[triethuynhmath]

Bài 78:
Cho $\Delta ABC$ có G là trọng tâm ,3 cạnh :a,b,c .Một điểm M bất kỳ.Đoạn thẳng MG =d
Tính $MA^2 +MB^2 +MC^2$ theo a,b,c,d

Bài này thấy căng quá mình giải được một cách dùng vectơ,tham khảo nhé,à tại sao em lại đặt dấu ngoặc kép vào chỗ "tự" vậy,dễ gây hiềm khích đó
Ta sẽ chứng minh điều sau:
$\overrightarrow{3MG}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$
Ta có :
Gọi F là trung điểm BC $3\overrightarrow{MG}=\overrightarrow{MA}+\overrightarrow{AG}+2\overrightarrow{MG}=\overrightarrow{MA}+2\overrightarrow{GF}+2\overrightarrow{MG}=\overrightarrow{MA}+2\overrightarrow{MF}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$.
Vậy bổ đề được chứng minh,bình phương 2 vế,ta được:
$9MG^2=MA^2+MB^2+MC^2+2(\overrightarrow{MA}.\overrightarrow{MB}+\overrightarrow{MB}.\overrightarrow{MC}+\overrightarrow{MC}.\overrightarrow{MA})$
Ta có theo tính chất tích vô hướng của vectơ,ta có :
$2\overrightarrow{MA}.\overrightarrow{MB}=2MA.MB.cos AMB=+MA^2+MB^2-BC^2$(Định lí hàm cos)
Thiết lập các đẳng thức tương tự rôi cộng vế theo vế ta được :
$9MG^2=MA^2+MB^2+MC^2+2(MA^2+MB^2+MC^2)-(AB^2+BC^2+CA^2)\Rightarrow MA^2+MB^2+MC^2=\frac{9d^2+a^2+b^2+c^2}{3}(Q.E.D)$
Bài toán được chứng minh hoàn toàn .
Cách này có vẻ khá "cấp 3".Ai có lời giải hay hơn thì post nhé,cách này có vẻ cũng không khó lắm chỉ cần nắm một số bổ đề về vectơ là xong nhưng nằm ngoài THCS

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 04-08-2012 - 22:38

[BlackSelena]

Bài này thấy căng quá mình giải được một cách dùng vectơ,tham khảo nhé,à tại sao em lại đặt dấu ngoặc kép vào chỗ "tự" vậy,dễ gây hiềm khích đó
Ta sẽ chứng minh điều sau:
$\overrightarrow{3MG}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$
Ta có :
Gọi F là trung điểm BC $3\overrightarrow{MG}=\overrightarrow{MA}+\overrightarrow{AG}+2\overrightarrow{MG}=\overrightarrow{MA}+2\overrightarrow{GF}+2\overrightarrow{MG}=\overrightarrow{MA}+2\overrightarrow{MF}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}$.
Vậy bổ đề được chứng minh,bình phương 2 vế,ta được:
$9MG^2=MA^2+MB^2+MC^2+2(\overrightarrow{MA}.\overrightarrow{MB}+\overrightarrow{MB}.\overrightarrow{MC}+\overrightarrow{MC}.\overrightarrow{MA})$
Ta có theo tính chất tích vô hướng của vectơ,ta có :
$2\overrightarrow{MA}.\overrightarrow{MB}=2MA.MB.cos AMB=+MA^2+MB^2-BC^2$(Định lí hàm cos)
Thiết lập các đẳng thức tương tự rôi cộng vế theo vế ta được :
$9MG^2=MA^2+MB^2+MC^2+2(MA^2+MB^2+MC^2)-(AB^2+BC^2+CA^2)\Rightarrow MA^2+MB^2+MC^2=\frac{9d^2+a^2+b^2+c^2}{3}(Q.E.D)$
Bài toán được chứng minh hoàn toàn .
Cách này có vẻ khá "cấp 3".Ai có lời giải hay hơn thì post nhé,cách này có vẻ cũng không khó lắm chỉ cần nắm một số bổ đề về vectơ là xong nhưng nằm ngoài THCS

Bài 78:
Cho $\Delta ABC$ có G là trọng tâm ,3 cạnh :a,b,c .Một điểm M bất kỳ.Đoạn thẳng MG =d
Tính $MA^2 +MB^2 +MC^2$ theo a,b,c,d
(p/s : bài này nghiêm cấm những ai học trên lớp 9 giải ,cấm đấy!!! thật đấy!!!! , khuyến khích BlackSelena *tự* làm)
----------------------------------------
Ai làm nốt bài 44 di

Lời giải bài 78 thuần THCS

Lấy $D$ là trung điểm $BC$; $H$ là trung điểm $AG$
Áp dụng công thức tính đường trung tuyến trong $\triangle MBC$ có:
$MD^2 = \frac{MB^2+MC^2}{2} - \frac{a^2}{4}$
Tương tự, ta cũng có
$MG^2 = \frac{MD^2+MH^2}{2} - \frac{HD^2}{4}$
$MH^2 = \frac{MG^2+MA^2}{2} - \frac{GA^2}{4}$
Vậy thế $MH^2$ vào công thức tính $MG^2$, ta có:
$MG^2 = \frac{MD^2+\frac{MG^2+MA^2}{2}+\frac{GA^2}{4}}{2}-\frac{HD^2}{4}$
$MG^2 =\frac{MD^2}{2} +\frac{MG^2+MA^2}{4} - \frac{GA^2}{8} -\frac{HD^2}{4}$
$\Rightarrow 8MG^2 = 4MD^2 + 2MG^2 + 2MA^2 - GA^2 - 2HD^2$
$\Rightarrow 4MD^2 = 6MG^2 - 2MA^2 + 3GA^2$
$\Rightarrow MD^2 = \frac{3MG^2}{2}-\frac{MA^2}{2} + \frac{3GA^2}{4}$
Mà ta lại có $MD^2 = \frac{MB^2+MC^2}{2} - \frac{a^2}{4}$ (chứng minh ở trên)
$\Rightarrow \frac{MB^2+MC^2}{2} = \frac{3MG^2}{2} - \frac{MA^2}{2} + \frac{3GA^2}{4} + \frac{a^2}{4}$
$\Rightarrow MB^2 + MC^2 + MA^2= 3MG^2 + \frac{3GA^2}{2} +\frac{a^2}{2}$
Mặt khác, ta cũng có
$\frac{3GA^2}{2} = \frac{2AD^2}{3} = \frac{AB^2+AC^2}{3} - \frac{BC^2}{6}$
Vậy $MA^2+MB^2+MC^2 = \frac{AB^2+AC^2}{3} + \frac{a^2}{2} - \frac{a^2}{6} + 3MG^2$
$=\frac{AB^2+AC^2+BC^2+9MG^2}{3}$
$=\frac{a^2+b^2+c^2+9d^2}{3}$
 

Bài viết đã được chỉnh sửa nội dung bởi nguyentrunghieua: 19-10-2013 - 23:12

[henry0905]

Bài 79:
Tứ giác ABCD có AB cắt CD tại E, AD cắt BC tại F. Chứng minh trực tâm các tam giác BCE,CDF,ADE,ABF nằm trên đường thẳng d, các trung điểm của các đoạn AC,BD,EF cùng nằm trên đường thẳng d' và d vuông góc d'
@@ Selena: Bài em giải hay thật. Tuy có thể chứng minh bằng toán 9 nhưng công thức tính đường trung tuyến trong tam giác thường là của chương trình hình học 10.
@@ H.Triết: Vectơ rồi cả tích vô hướng. Bài của chú "sặc mùi" lớp 10 .

[yeutoan11]

Chào đồng nghiệp henry. CT tính trung tuyến nếu vào đội tuyển thì sẽ học thôi ^^, mà bài hình đó nằm ở đẳng cấp tỉnh trở lên ấy chứ
P/S : Có yahoo cho xin anh em ta tâm sự =))

[BoFaKe]

Trước hết yêu cầu @True09 và em @blackselena không cãi nhau gây mất đoàn kết nữa,không admin vào 2 người ra đảo đấy.

Lời giải bài 78 thuần THCS

Lấy $D$ là trung điểm $BC$; $H$ là trung điểm $AG$
Áp dụng công thức tính đường trung tuyến trong $\triangle MBC$ có:
$MD^2 = \frac{MB^2+MC^2}{2} - \frac{a^2}{4}$
Tương tự, ta cũng có
$MG^2 = \frac{MD^2+MH^2}{2} - \frac{HD^2}{4}$
$MH^2 = \frac{MG^2+MA^2}{2} - \frac{GA^2}{4}$
Vậy thế $MH^2$ vào công thức tính $MG^2$, ta có:
$MG^2 = \frac{MD^2+\frac{MG^2+MA^2}{2} - \frac{GA^2}{4}}{2} - \frac{HD^2}{4}$
$MG^2 = \frac{MD^2} + \frac{MG^2+MA^2}{4} - \frac{GA^2}{8} -\frac{HD^2}{4}$
$\Rightarrow 8MG^2 = 4MD^2 + 2MG^2 + 2MA^2 - GA^2 - 2HD^2$
$\Rightarrow 4MD^2 = 6MG^2 - 2MA^2 + 3GA^2$
$\Rightarrow MD^2 = \frac{3MG^2}{2}-\frac{MA^2}{2} + \frac{3GA^2}{4}$
Mà ta lại có $MD^2 = \frac{MB^2+MC^2}{2} - \frac{a^2}{4}$ (chứng minh ở trên)
$\Rightarrow \frac{MB^2+MC^2}{2} = \frac{3MG^2}{2} - \frac{MA^2}{2} + \frac{3GA^2}{4} + \frac{a^2}{4}$
$\Rightarrow MB^2 + MC^2 + MA^2= 3MG^2 + \frac{3GA^2}{2} +\frac{a^2}{2}$
Mặt khác, ta cũng có
$\frac{3GA^2}{2} = \frac{2AD^2}{3} = \frac{AB^2+AC^2}{3} - \frac{BC^2}{6}$
Vậy $MA^2+MB^2+MC^2 = \frac{AB^2+AC^2}{3} + \frac{a^2}{2} - \frac{a^2}{6} + 3MG^2$
$=\frac{AB^2+AC^2+BC^2+9MG^2}{3}$
$=\frac{a^2+b^2+c^2+9d^2}{3}$

@@ Selena: Bài em giải hay thật. Tuy có thể chứng minh bằng toán 9 nhưng công thức tính đường trung tuyến trong tam giác thường là của chương trình hình học 10.

@blackselena:tuyệt đấy,anh cũng còn phải học hỏi nhiều
@henry0905:đâu có,mình học công thức tính trung tuyế,phân giác,hê-rông từ hồi hè lớp 8 cơ.Cái này chỉ dùng trong thi giải toán máy tính casio thôi chứ thi HSG kia là phải chứng minh

[L Lawliet]

Bài 79: Cho tứ giác lồi có diện tích $32$, tổng của hai cạnh đối diện và một đường chéo bằng $16$. Hãy xác định những độ dài có thể có của đường chéo kia.

Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 06-08-2012 - 13:34

[ntm1406]

Bài 80: CMR: Nếu hình vuông có diện tích không lớn hơn diện tích tam giác thì hình vuông có chu vi nhỏ hơn chu vi tam giác ấy.

[triethuynhmath]

Bài 80: CMR: Nếu hình vuông có diện tích không lớn hơn diện tích tam giác thì hình vuông có chu vi nhỏ hơn chu vi tam giác ấy.

Chém bài này :
Gọi a là độ dài hình vuông ,x,y,z là độ dài 3 cạnh tam giác,h là 1 đường cao ứng với cạnh x của tam giác.
Theo giả thiết,ta có :
$a^2\leq \frac{1}{2}h.x\Rightarrow 2a^2\leq hx\Rightarrow a\sqrt{2}\leq \sqrt{hx}\Rightarrow 2a\leq \sqrt{2hx}\Rightarrow 4a\leq 2\sqrt{2hx}\leq 2h+x(Cauchy)$
$< x+y+z$(Tính chất đường xiên đường vuông góc).
Vậy chu vi hình vuông < chu vi tam giác $(Q.E.D)$

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 06-08-2012 - 13:31

[BlackSelena]

Đây có lẽ là những bài chấm dứt cho "sê-ri" tính góc của em .
Bài 81: Cho $\triangle ABC$ nhọn. Dựng các tam giác đều $ABC'$ và $AB'C$ ra ngoài $\triangle ABC$. Gọi $K$ và $l$ theo thứ tự là trung điểm $C'A$ và $B'C$ , $M$ là một điểm trên cạnh $BC$ sao cho $BM = 3MC$. Tính các góc của $\triangle KLM$
Bài 82: $\triangle ABC$ có $\angle A= 75^o$. Tính các góc còn lại của tam giác, biết rằng có một đường thẳng đi qua đỉnh $A$ và chia $\triangle ABC$ thành 2 tam giác cân.

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 06-08-2012 - 16:08

[C a c t u s]

Bài 82: $\triangle ABC$ có $\angle A= 75^o$. Tính các góc còn lại của tam giác, biết rằng có một đường thẳng đi qua đỉnh $A$ và chia $\triangle ABC$ thành 2 tam giác cân.

Ta có: $\angle AEB = \angle EAC + \angle ACE$
Mà $\angle AEB = \angle ABE$
$\Rightarrow \angle EAC + \angle ACE=\angle ABE$
Mà $\angle EAC = \angle ACE$
$\Rightarrow 2\angle ACE= \angle ABE$
Hay $2\angle ACB= \angle ABC$
$\Rightarrow \angle ACB=35^o ; \angle ABC=70^o$
P.s: Mình có hiểu nhầm đề không nhỉ
_______________
Chuẩn k cần chỉnh, thật sự bài này mình đặt $ACB= \alpha$

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 06-08-2012 - 16:24

[BlackSelena]

Bài 79: Cho tứ giác lồi có diện tích $32$, tổng của hai cạnh đối diện và một đường chéo bằng $16$. Hãy xác định những độ dài có thể có của đường chéo kia.

Cụm từ "đường chéo kia" mờ ẩn quá.
Nếu là tính cái đường chéo mà nằm trong cái tổng bằng 16 thì em xin tính như sau.
Xét tứ giác $ABCD$ có đường chéo $BD$.
Kẻ $DM \perp AB$, $BN \perp DC$
Khi đó ta có
$S_{ABCD} = S_{ABD} + S_{BCD} = \frac{DM.BD+BN.BD}{2} \leq \frac{BD(DM+BN)}{2} = \frac{BD(16-BD)}{2} \leq 32$
Dấu bằng xảy ra khi $BD =8$. $AD\perp AB, BC \perp DC$
Mà dấu bằng xảy ra nên .....
Tính đg chéo kia chắc là được nhưng lẻ lắm @@

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 06-08-2012 - 21:39

[L Lawliet]

Cụm từ "đường chéo kia" mờ ẩn quá.
Nếu là tính cái đường chéo mà nằm trong cái tổng bằng 16 thì em xin tính như sau.
Xét tứ giác $ABCD$ có đường chéo $BD$.
Kẻ $DM \perp AB$, $BN \perp DC$
Khi đó ta có
$S_{ABCD} = S_{ABD} + S_{BCD} = \frac{DM.BD+BN.BD}{2} \leq \frac{BD(DM+BN)}{2} = \frac{BD(16-BD)}{2} \leq 32$
Dấu bằng xảy ra khi $BD =8$. $AD\perp AB, BC \perp DC$
Mà dấu bằng xảy ra nên .....
Tính được chéo kia chắc là được nhưng lẻ lắm @@

Giải:
Giả sử $x$ là độ dài của đường chéo $AC$ mà tổng của nó với hai cạnh đối diện $AD$, $BC$ của tứ giác là $16$. Hạ $DK\perp AC$ và $BH\perp AC$.
Đặt $y=BH+DK$, gọi $S$ là diện tích tứ giác, ta có $S=\frac{xy}{2}$.
Theo giả thuyết ta có: $AD+BC=\left ( 16-x \right )$, mà vì cạnh huyền là cạnh lớn nhất trong một tam giác vuông nên $y$ có giá trị lớn nhất là $\left ( 16-x \right )$, điều này xảy ra khi $K\equiv A$, $H\equiv C$. Lúc đó, tứ giác đã cho có $AD$ và $BC$ vuông góc với $AC$. Mặt khác, ta có:
$\frac{x\left ( 16-x \right )}{2}=\frac{64-\left ( x-8 \right )^2}{2}\leq \frac{64}{2}=32$, đẳng thức xảy ra khi $x=8$. Vì theo giả thuyết, diện tích tứ giác là $32$ nên ta có $x=8$.
Điều này xảy ra khi: $y=BH+DK=8$. Lúc này dễ thấy độ dài đường chéo kia là: $BD=BI+ID=2.4\sqrt{2}=8\sqrt{2}$.
----
Đang ngồi ở quán net nên không vẽ hình được TT^TT

Bài viết đã được chỉnh sửa nội dung bởi L Lawliet: 06-08-2012 - 21:38

[triethuynhmath]

Bài 83:
Cho tam giác ABC nhọn 3 đường cao AD,BE,CF cắt nhau tại trực tâm H.EF cắt BC tại T.
TH cắt AC tại R.Chứng minh rằng :
$AE.RC=ER.AC$
Lưu ý:Bác binhmetric và mọi người đừng dùng hàng điểm điều hòa nhé vì lúc đó bài sẽ rất dễ

Bài viết đã được chỉnh sửa nội dung bởi triethuynhmath: 07-08-2012 - 16:26

[Tru09]

Kết thúc seri tính góc của BlackSelena
Lấy M' là trung điểm AC , J là trung điểm BC
$\text{Lấy I Đối xứng L qua M}$
ta có :
$KA=\frac{1}{2}C'A =\frac{1}{2} AB=M'J$
$AL=B'M' :\text{(là đường cao trong tam giác đều)}$
$\angle KAL =60^o +30^o +\angle BAC=90^o +\angle JM'C=\angle JMB'$
$\rightarrow \Delta KAL =\Delta JM'B'$
$\rightarrow KL =JB'(1)$
Bên cạnh đó:
vì I đối xứng L qua M và M' là trung điểm JC
$\rightarrow \Delta JIM =\Delta CLM$
$\rightarrow IJ =LC=LB'$
$\rightarrow IJB'L :\text{hình bình hành}$
$\rightarrow JB' =IL(2)$
Từ $(1) $và$ (2) \rightarrow IL=KL$
$\rightarrow KL=2ML(3)$
Mà từ
$\Delta KAL =\Delta JM'B'$
$\rightarrow \angle M'B'J =\angle ALK$
Ta có : $\angle ALK +\angle MLC$
$=\angle M'B'J +\angle JB'L=30^o$
$\rightarrow \angle KLM =90^o -30^o =60^o(4)$
Từ $(3)$ và$ (4) \rightarrow \Delta KML :\text{là nửa tam giác đều}$
$\rightarrow \angle MKL =30^o ;\angle KML =90^o ;\angle KLM=60^o$

Hình gửi kèm

• 

Bài viết đã được chỉnh sửa nội dung bởi Tru09: 07-08-2012 - 14:13

[BlackSelena]

Bài 83:
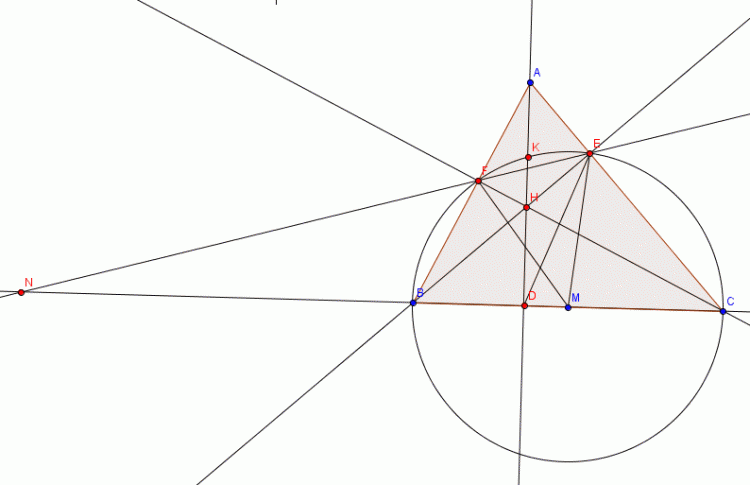
Cho tam giác ABC nhọn 3 đường cao AD,BE,CF cắt nhau tại trực tâm H.EF cắt BC tại T.
TH cắt AC tại R.Chứng minh rằng :
$AE.RC=ER.AC$
Lưu ý:Bác binhmetric và mọi người đừng dùng hàng điểm điều hòa nhé vì lúc đó bài sẽ rất dễ

Làm xong bài này của anh cũng nổ não.

Ban đầu đã thử với cách xài $Menelaus$ nhưng tự nhận ra là đang tự sát.
$TR \cap AM = I$, trước hết ta sẽ (phải) chứng minh $AD \perp TM$, hay tức là $H$ là trực tâm $\triangle AMT$
Vẽ đường tròn tâm $O$ ngoại tiếp $\triangle ABC$, cắt $AT$ tại $K$, ta sẽ đi chứng minh $H,M,K:\text{ thẳng hàng}$
Lưu ý, theo phương tích của điểm nằm ngoài đường tròn (cụ thể là điểm $T$) thì ta có:
$TK.TA=TF.TE=TB.TC$
$\Rightarrow \triangle TKF \sim \triangle TEA$
$\Rightarrow \angle TKF = \angle TEA$
$\Rightarrow KFEA:tgnt$(1)
Mà dễ thấy $AEHK:tgnt$(2)
Từ $(1)$ và $(2) \Rightarrow A,E,H,K,F:\text{ đồng viên}$.
$\Rightarrow HK \perp AT$
Mình lưu ý bôi đỏ vì ta ở đây mới chúng minh được $HK \perp AT$ chứ chưa chứng minh được $H,M,K$ thẳng hàng.
Và giờ là công đoạn chứng minh $K,H,M:\text{thẳng hàng}$, cũng hại não không kém.
Kẻ đường kính $AD$, ta sẽ chứng minh một thứ "mạnh" hơn đó là $K,H,M,D:\text{ thẳng hàng}$.
Nghe thì có vẻ khủng nhưng thực chất nó là mấu chốt để ta chứng minh $K,H,M:\text{thẳng hàng}$
$AD$ là đường kính $\Rightarrow BD \perp AB, DC \perp AC$
Mặt khác cũng có $CH \perp AB, BH \perp AC$
$\Rightarrow BHCD:\text{hình bình hành}$
$\Rightarrow H,M,D:\text{thẳng hàng}$ (*). Tới đây là phần quan trọng của việc chứng minh thẳng hàng.
Phần còn lại cũng khá dễ, ta có $DK \perp AT$ mà $KH \perp AT$ (đã chứng minh ở trên).
$\Rightarrow K,H,D:\text{thẳng hàng}$. (**)
Từ $(*) \text{ và } (**)$ ta có $K,H,M,D:\text{ thẳng hàng}$.
Vậy $K,H,M:\text{ thẳng hàng}$
$\Rightarrow MH \perp AT$
$\Rightarrow H$ là trực tâm $\triangle AMT$
$\Rightarrow TR \perp AM$
Vậy ta đã chứng minh được mớ ba lăng nhăng mà em nêu ra ở đầu bài, và cũng là mấu chốt bài toán.
Dễ thấy $AEIH:tngt$
$\Rightarrow \angle EIR = \angle HAC$ (^)
Mặt khác, ta cũng có
$FHIE:tgnt$ do $\angle EHE$ và $\angle FIE$ cùng bù với $\angle KAE$
$\Rightarrow TH.TI = TF.TE$
Mặt khác, theo phương tích ta lại có $TF.TE = TB.TC$
$\Rightarrow TH.TI=TB.TC$
$\Rightarrow HICB:tgnt$
$\Rightarrow \angle RIC = \angle HBD$
Mặt khác cũng dễ thấy $\angle HBD = \angle HAC$
$\Rightarrow \angle RIC = \angle HAC$ (^^)
Từ (^) và (^^) $\Rightarrow \angle EIR = \angle RIC$
$\Rightarrow IR:\text{ phân giác } \angle EIC$
Mà ta lại có $\angle AIR = 90^o$
Vậy $AI, IR$ lần lượt là tia phân giác của 2 góc kề bù.
Vậy $AI$ là tia phân giác của góc ngoài $\angle EIC$
Áp dụng tính chất đường phân giác góc ngoài, góc trong luôn, ta có
$\frac{ER}{RC} = \frac{IE}{IC} = \frac{AE}{AC}$
$\Rightarrow ER.AC = AE.RC$ (đpcm)
P/s:

Bài viết đã được chỉnh sửa nội dung bởi BlackSelena: 07-08-2012 - 23:20