Chủ đề này có 3 trả lời

[anh qua]

Pro: Cho tam giác $ABC$, gọi $M_{a};M_{b};M_{c}$ là trung điểm 3 cạnh $BC,CA,AB$. $(I)$ là đường tròn nội tiếp tam giác tiếp xúc với $BC;CA;AB$ tại $A_{1};B_{1};C_{1}. AI, BI,CI$ cắt $BC,CA,AB$ tại $ X,Y,Z$. Từ $X$ kẻ tiếp tuyến với $(I)$ cắt đường thẳng qua $A_{1}$ vuông góc với $IM_{a}$ tại $X_{a}$. Xây dựng tương tự $X_{b}; X_{c}$ . Chứng minh rằng:
$X_{a};X_{b};X_{c}$ thẳng hàng và đường thẳng này tiếp xúc với $(I)$

Bài viết đã được chỉnh sửa nội dung bởi anh qua: 31-07-2012 - 07:24

[anh qua]

Gợi ý: Dùng điểm Feuerbach và phép vị tự!

[chinhanh9]

Có sai sót gì xin chỉ giáo!
Để giải bài toán này ta cần có hai bổ đề:
Bổ đề 1: (Cho tam giác và gọi tên các điểm như ở đề bài toán) (hình đầu tiên)
Đường thẳng qua $X$ tiếp xúc với $\left ( I \right )$ tại $A_{2}$. Tương tự đối với $B_{2},C_{2}$. Khi đó, ta có: $M_{a}A_{2}, M_{b}B_{2}, M_{c}C_{2}$ đồng quy tại điểm $F$ - chính là điểm Feuerbach của tam giác $ABC$.
Bổ đề 1 được Chinhanh9 phát hiện dựa vào thực nghiệm, chưa biết chứng minh.
Bổ đề 2: (quen thuộc nên cũng xin không chứng minh) (hình thứ hai)
Cho đường tròn $\left ( O \right )$, $MA,MB$ là hai tiếp tuyến. Vẽ cát tuyến $MCD$. Khi đó, hai tiếp tuyến của $\left ( O \right )$ tại $C, D$ và đường thẳng $AB$ đồng quy tại điểm $I$.
Trở lại với bài toán của anh qua: (hình cúng cuồi)
Qua$X$ kẻ đường thẳng tiếp xúc với $\left ( I \right )$ tại $A_{2}$. Đường thẳng qua $A_{1}$ và vuông góc với $IM_{a}$ cắt $\left ( I \right )$ tại $A_{3}$, thì $MA_{3}$ là tiếp tuyến của $\left ( I \right )$. Theo đề thì $X_{a}$$= A_{1}A_{3}\cap XA_{2}$. Theo bổ đề 1, ta có $F = MA_{2}\cap \left ( I \right )$. Theo bổ đề 2, $X_{a}$ thuộc đường thẳng $d$ đi qua $F$ và tiếp xúc với $\left ( I \right )$. Suy ra điều tương tự đối với $X_{b}, X_{c}$. Từ đó ta được ĐPCM.

Hình gửi kèm

• 
• 
• 

Bài viết đã được chỉnh sửa nội dung bởi chinhanh9: 07-08-2012 - 14:01

[perfectstrong]

Một cách giải khác, cũng chưa hoàn chỉnh lắm
Lời giải 2:
Vẽ $IM_a \perp A_1X_a$ tại $Q$. Vẽ $XX_a$ tiếp xúc $(I)$ tại $T$. $M_aT$ cắt $X_aA_1$ tại $F_a$. $IF_a$ cắt $M_aX_a$ tại $G$.
$\vartriangle M_aA_1I$ vuông tại $A_1$ có đường cao $A_1Q$ nên $IQ.IM_a=IA_1^2=IT^2$
$\Rightarrow \vartriangle IQT \sim \vartriangle ITM_a(c.g.c) \Rightarrow \angle ITQ=\angle IM_aT$.
Mà $\angle IQX_a=\angle ITX_a=90^o \Rightarrow I,Q,T,X_a$ đồng viên. Do đó $\angle ITQ=\angle IX_aQ$
$\Rightarrow \angle IX_aQ=\angle IM_aT \Rightarrow \angle IM_aT+\angle M_aIX_a=90^o \Rightarrow M_aF_a \perp IX_a$ tại $K$.
Suy ra $F_a$ là trực tâm của $\vartriangle X_aIM_a \Rightarrow IF_a \perp M_aX_a$.
Do đó, ta có $\overline{X_aG}.\overline{X_aM_a}=\overline{X_aK}.\overline{X_aI}=X_aT^2,(1)$.

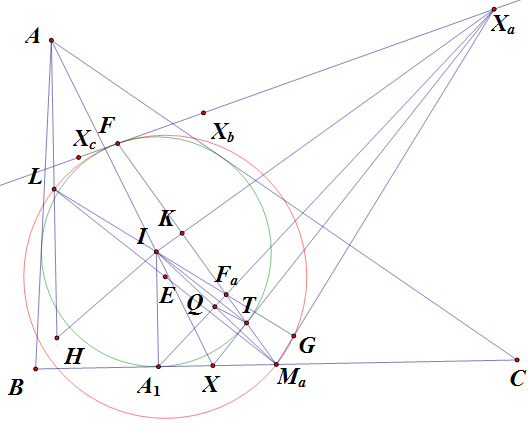
Vẽ $IG$ cắt $AH$ tại $L$. Chứng minh được $(IH,IX,IA_1,IG)=-1$. Từ đó, do $AH \parallel IA_1$ nên $L$ là trung điểm của $AH$.
Đường tròn Euler $(E)$ của $\vartriangle ABC$ có đường kính là $LM_a$ và $\angle LGM_a=90^o \Rightarrow G \in (E)$.
$(1) \Rightarrow P_{X_a/(I)}=P_{X_a/(E)}$ nên $X_a$ thuộc trục đẳng phương $d$ của 2 đường tròn $(E),(I)$.
Tương tự, $X_b;X_c \in d$ nên $X_a;X_b;X_c$ thẳng hàng.
Mà do $(E)$ tiếp xúc $(I)$ tại $F$ là điểm Feurerbach nên $d$ tiếp xúc với $(I)$ tại $F$.