Chủ đề này có 2 trả lời

[thanhluong]

Cho tam giác ABC vuông tại A. Lấy điểm P nằm trong tam giác. Gọi PE, PF, PQ lần lượt là đường vuông góc kẻ từ P đến AC, AB, BC. Xác định P để $PE^2+PF^2+PQ^2$ đạt giá trị bé nhất

[ntuan5]

$AH$ là đường cao
$AEPF$ là hình vuông$\rightarrow PE^2+PF^2+PQ^2=AP^2+PQ^2 \ge \frac{(AP+PQ)^2}{2} \ge \frac{AH^2}{2}$
Vậy GTNN là $\frac{AH^2}{2}$

Đẳng thức xảy ra khi:

$AP=PQ$ hay $P$ là trung điểm $AH$.

Bài viết đã được chỉnh sửa nội dung bởi ntuan5: 07-08-2012 - 16:55

[nthoangcute]

Tham khảo ở đây: http://diendantoanho...nta98ka-vs-all/

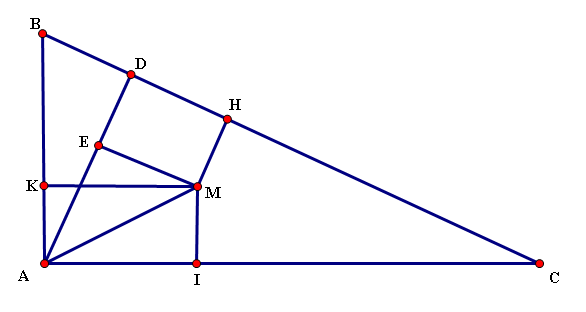
Cho $\Delta ABC$ vuông tại $A$. $M$ là một điểm di động bên trong $\Delta ABC$. Họi $H,I,K$ là chân các hình chiếu của $M$ lên các cạnh $BC,CA,AB$. Tìm vị trí của điểm $M$ sao cho:
$MI^2+MH^2+MK^2$ đạt $Min$

Vẽ đường cao AD , ME vuông góc AD tại E
Ta có $\angle KAI = \angle MKA = \angle MIA=90^{\circ}$
$\Rightarrow AKMI$ là hình chữ nhật
$\Rightarrow MK^2+MI^2=KI^2=AM^2$
Lại có
$\angle MED=\angle MHD=\angle EDH= 90^{\circ}$
$\Rightarrow MEDH$ là HCN
$\Rightarrow MH=ED$
$\Rightarrow MI^2+MK^2+MH^2=MA^2+ED^2\geq EA^2+ED^2\geq \frac{(EA+ED)^2}{2}=\frac{AD^2}{2}$
Dấu "=" xảy ra khi E trùng M và EA=ED tương đương M là trung điểm AD
Vậy khi M là trung điểm của đường cao AD thì $MI^2+MK^2+MH^2$ nhỏ nhất

Bài viết đã được chỉnh sửa nội dung bởi nthoangcute: 07-08-2012 - 16:53