Cho $\bigtriangleup ABC$ có trực tâm $H$ chia đường cao $CC'$ làm $2$ phần bằng nhau. CMR:
$\cos C=\cos A.\cos B$
Bài 2:Cho $\bigtriangleup ABC$. Trên các cạnh $BC, CA, AB$ lấy điểm $M,N,E$ sao cho: $\frac{MA}{MB}=\frac{NB}{NC}=\frac{EC}{EA}=\frac{1}{4}$
Các đường $AN,BE,CM$ cắt nhau tại $L,D,F$. CMR: \[\frac{{S_{LDF} }}{{S_{ABC} }} = \frac{3}{7}\]
Bài 3:
Cho $\bigtriangleup ABC$. Trên cạnh $BC,CA,AB$ lấy $A',B',C'$ sao cho $AA',BB',CC'$ đồng qui tại $M$. CMR:
- $\frac{MA'}{AA'}+\frac{MB'}{BB'}+\frac{MC'}{CC'}=1$
- $\frac{AM}{AA'}+\frac{BM}{BB'}+\frac{CM}{CC'}=2$
- $\frac{MA}{MA'}=\frac{B'A}{B'C}+\frac{C'A}{C'B}$
Cho $\bigtriangleup ABC$. Trên cạnh $BC$ lấy điểm $D$. Đặt $AD=d$, $BD=m$, $CD=n$. CMR:\[d^2 a = b^2 m + c^2 n - amn\]
Bài 5:
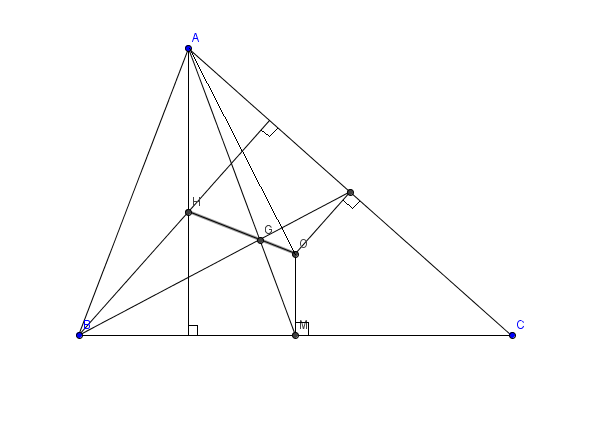
Cho $\bigtriangleup ABC$ có $H,G,O$ lần lượt là trực tâm, trọng tâm và tâm đường tròn ngoại tiếp $\bigtriangleup ABC$
- CMR:$ OG=\frac{1}{3}\sqrt{9R^2-(a^2+b^2+c^2)}$
- Tính $GH$
Bài viết đã được chỉnh sửa nội dung bởi Nguyen Lam Thinh: 24-11-2012 - 15:59