canhhoang30011999

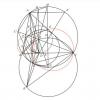
1 cách khác cho bài 2 

gọi $B_{1}, C_{1}$ là điểm đối xứng của $B$ $C$ qua $IC$ và $IB$ thì theo bổ đề 1 ở đây thì $B_{1}C_{1}$ vuông góc với $OI$

$OI$ cắt $(IAC)$ ở $D'$ $IJ'$ vuông góc với $CD'$ ($J'$ thuộc (IAC)) ta chứng minh $J$ và $J'$ đối xứng với nhau qua $OI$

ta có $\angle {DJI}=90-\angle {IBD}=90-\angle {BAI}$

tương tự ta có $\angle {DIJ'}= 90=\angle {IAC}$

từ đó ta có $\angle {DIJ}=\angle {DIJ'}$

ta có $\angle {JB_{1}C} =\angle {ABJ} =180 -\angle {AIJ}=180- \angle {AID} -90+ \angle {BAI}=90- \angle {B_{1}PI}$ ($OI$ cắt $AC$ tại $P$)

nên $B_{1}J$ vuông góc với $OI$

tương tự $C_{1}J'$ vuông góc với $OI$ nên $JJ'$ vuông góc với $OI$ ta có đpcm

6

ta có $\sum \frac{a} {b^{3}+4}= \sum \frac{a} {4} -\frac{ab^{3}} {4(b^{3}+4)} \geq \sum \frac{a} {4} - \frac{ab} {12}$

$=1-\frac{ab+bc+cd+da} {12} \geq 1- \frac{(a+c)(b+d)} {12} \geq \frac{2} {3}$

dấu bằng xảy ra khi $a=d=2, b=c=0$

Bài 71: Tìm tất cả các số nguyên dương $n$ thỏa mãn : không có số chính phương $m$ nào sao cho $n<m<2n$

bài toán tương đương với tồn tại x sao cho $x^{2} \leq n<2n \leq (x+1)^2$ từ đó suy ra $2x^{2}<(x+1)^{2}$ đánh giá chặn được n

Trên thanh địa chỉ em thấy có chữ https, em bỏ chữ 's' đi để còn http thôi rồi nhấn enter xem có được không nhé.

chắc sau khi sửa cái link cũ của em bị hỏng vì nếu em ấn vào chữ  Trang chủ trong hình thì vẫn vào được

Cho em hỏi giao diện của diễn đàn hiện tại là thế này hay máy em bị lỗi ạ