IHateMath

$\boxed{\text{Bài toán 2}}$ (British MO 2014) 

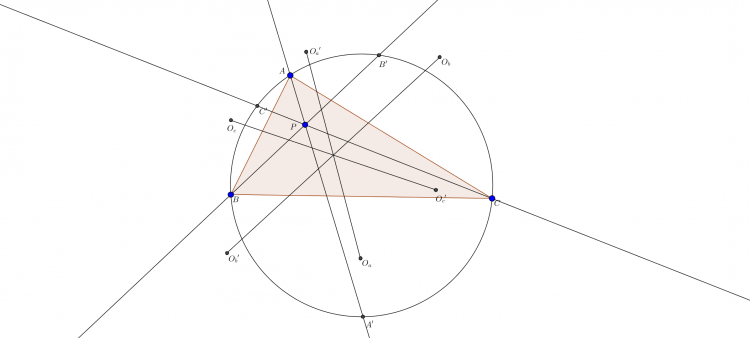
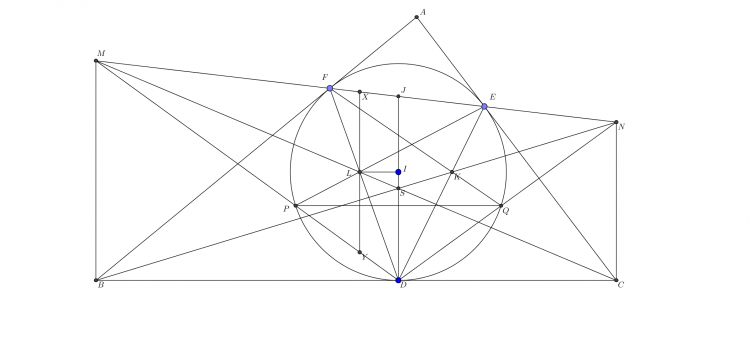
Cho tam giác $ABC$ và điểm $P$ nằm trong tam giác. Gọi giao điểm thứ hai của $AP$ với $(ABC)$ là $A'$. Các điểm $B',C'$ được xác định tương tự. Gọi $O_{a}$ là tâm đường tròn $(BCP)$. Các điểm $O_{b},O_{c}$ xác định tương tự. Gọi $O_{a}'$ là tâm đường tròn $(B'C'P)$.Các điểm $O_{b}',O_{c}'$ xác định tương tự. Chứng minh rằng $O_{a}O{a}',O_{b}O_{b}',O_{c}O_{c}'$ đồng quy.

Hình vẽ bài toán

Mình xin trình bày bài giải khác, hầu như chỉ sử dụng kiến thức lớp 7 (tam giác bằng nhau, tính góc cơ bản, v.v) . Ở đây để tiện quan sát mình đã trình bày bài toán dưới dạng các bổ đề nhỏ (chia nhỏ bài toán ra). Ý tưởng của mình là chứng minh  các cặp điểm $(E;I),(K;X),(L;F)$ đối xứng qua một đường qua $O$ sau đó chỉ cần chứng minh $X,E,L\in$ một đường tròn tâm $O$ là xong. Điều này có được là nhờ sự đặc biệt của bài toán. Sau đây xin được cụ thể hóa ý tưởng này.

Trước hết, gọi $T,N$ lần lượt là giao điểm của $AI,CK$, của $OE, (ABC)$. Dễ thấy $\angle TAC=\angle TCA=30^0\Rightarrow \angle ATC=120^0, \Delta ATC$ cân tại $T$. Suy ra $TO\bot AC$ chia đôi góc $ATC$. Hơn nữa $O,N$ đối xứng qua $BC$, tam giác $OBN$ đều. Các góc sau cũng tính được dễ dàng: $\angle BCK=\angle TCI=10^0, \angle ANO=20^0,\angle OET=80^0$.

$\boxed{\text{Bổ đề 1}}$: $K,X$ đối xứng qua $TO$.

Ta có $\angle AXO=\angle BAX+\angle ABX=\frac{60^0}{2}+80^0-30^0=80^0.$. Mặt khác $\angle OKC=\angle KMC+\angle KCM=\angle NMC+\angle KCM=90^0-20^0+10^0=80^0$ (do $O,N$ đối xứng qua $BC$, tam giác $OBN$ đều). Kết hợp với $TO$ là tia phân giác góc $ATC$ suy ra $\Delta OTK=\Delta OTX\Rightarrow K,X$ đối xứng qua $TO$.

$\boxed{\text{Bổ đề 2}}$: $I,E$ đối xứng qua $TO$.

Thật vậy, theo một kết quả rất quen thuộc $NI=NB$, mặt khác ta đã chứng minh được $NB=NO$ nên $NI=NO$. Vậy $\Delta NOI$ cân tại $N$ và $\angle NIO=\frac{180^0-\angle ANO}{2}=80^0=\angle OET$. Vậy $\Delta OET=\Delta OIT\Rightarrow E,I$ đối xứng qua $OT(đ.p.c.m)$.

$\boxed{\text{Bổ đề 3}}$: $L,B$ đối xứng qua $AT$.

Thật vậy, dựng tia đối xứng với $AE$ cắt $BC$ tại $E'$. Ở bổ đề 2, ta đã chứng minh được $E,I$ đối xứng qua $TO$ mà $\Delta TAC$ cân tại $T$, vậy $\angle TAE=\angle TCI=10^0\Rightarrow \angle TAE'=10^0$. Mặt khác ta cũng có $\angle TCE'=10^0$ nên $\Delta AE'C$ cân tại $E'$, và vì vậy $E',T,O$ thẳng hàng, suy ra $\angle ATE'=\angle CTE'=120^0=\angle ATE$. Suy ra $\Delta ATE'=\Delta ATE\Rightarrow E,E'$ đối xứng qua tia phân giác góc $BAC$. vậy tia $ME$ đối xứng với $ME'$ qua $AI\Rightarrow B,L$ dối xứng qua $AI$. Phép chứng minh bổ đề 3 hoàn thành.

Tới đây ta sẽ vào bài:

Theo bổ đề 3, ta có $\angle XLA=\angle XBA=90^0-\angle ACB$, mà $\angle KFC=90^0-\angle ACB$ (do $KF\bot BC$) nên $\angle KFL=\angle XLF$ kết hợp với bổ đề 2 ta suy ra $F,L$ đối xứng qua $TO$. Công việc còn lại là đi chứng minh $E,X,L\in$ 1 dường tròn tâm $O$. Ta có $\angle XOE=60^0, \angle XTE=120^0\Rightarrow XTEO$ nội tiếp. Hơn nữa, theo một kết quả cơ bản khác, $TO$ là tia phân giác $\angle XTE$ suy ra $\Delta XOE$ cân tại $O$ và nó thực sự là một tam giác đều. Tiếp tục, $\angle XLE=\angle XBC=30^0$ (theo bổ đề 3) nên ta có $X,E,L$ nội tiếp một dường tròn tâm $O$ là $Γ$. Dễ thấy theo tính chất đối xứng từ các bổ đề 1, 2 ta có $K,X,I,E,L,F\in Γ, đ.p.c.m$!

P/s: Ta có thêm một số kết quả sau:

1) $KF, XL, TO, CI, AE$ đồng quy tại $S$.

2) Gọi $J$ là giao điểm của đường cao hạ từ $C$ xuống $AB$ với $(ABC)$ thì $J,O,I$ thẳng hàng.

và còn nhiều kết quả khác, mời các bạn khám phá.

$$\begin{array}{| I | l |} \hline Ngockhanh99k48 & 1\\ \hline IHateMath & 1\\ \hline \end{array}$$

với $k$ là số nguyên dương sao cho: $k\geq 5$ và số nguyên tố $p$ sao cho: $p\geq k$  

cmr: $(2p+1)^3\leq (2k-1)^3 +\sum_{j=k}^{p}(2j-1)^3$

Đầu tiên ta sẽ cmr $(2n+1)^3\leq 2.(2n-1)^3(\forall n\geq 5)(1)$. Thật vậy, điều này tương đương với $\sqrt[3]{2}.(2n-1)-(2n+1)\geq 0\Leftrightarrow 2(\sqrt[3]{2}-1)n\geq \sqrt[3]{2}+1\Leftrightarrow n\geq \frac{\sqrt[3]{2}+1}{2(\sqrt[3]{2}-1)}\Leftrightarrow n\geq 4,347...$, đúng.

Hiển nhiên với $p=k=5$ ta có $đpcm$ vì khi đó bất đẳng thức cần cm trở thành $(1)$.

Bây giờ, áp dụng bất đẳng thức trên cho $p\geq 7,k\geq 5$ với chú ý rằng $(2q-1)^3\leq 2.[2(q-1)-1]^3(\forall q\geq 6)$ (nếu ta thay $q$ bởi $q+1$ sẽ thu được bất đẳng thức $(1)$) ta có:

$(2p+1)^3\leq 2.(2p-1)^3\leq 2.[2(p-1)-1]^3+(2p-1)^3\leq 2.[2(p-2)-1]^3+[2(p-1)-1]^3+(2p-1)^3\leq...\leq (2(p-(p-k-1))-1)^3+\sum\limits_{j=p-(p-k-1)}^{p}{(2j-1)^3}\leq (2(p-(p-k))-1)^3+\sum\limits_{j=p-(p-k)}^{p}{(2j-1)^3}=(2k-1)^3+\sum\limits_{j=k}^{p}{(2j-1)^3}(đpcm)$.

P/s: Mình nghĩ bất đẳng thức này không xảy ra dấu bằng do $(1)$ không xảy ra dấu bằng. Hơn nữa không cần giả thiết là $p$ nguyên tố mà chỉ cần $p\geq k\geq 5$ là được. Liệu có thể làm chặt hơn không?

(British MO 1997 R2 P3) Tìm số đa thức bậc $5$ với hệ số phân biệt lấy từ tập hợp {$1,2,3,4,5,6,7,8$} mà chia hết cho đa thức $x^2-x+1$.

Mấy bạn nào giỏi link chỉ mình xem bài toán này có xuất xứ từ đâu vậy: (không cần lời giải vì có nhiều trên diễn đàn này rồi )

Cho $a,b,c$ là các số thực dương thỏa mãn $ab+bc+ca+abc\le 4$. CMR $a+b+c\ge ab+bc+ca$.

Một số bài viết trên forum chú thích thêm rằng đây là bài trong kỳ thi học sinh giỏi quốc gia 1995 (có bài ghi là 1996) nhưng trên thực tế mình không tìm thấy bài nào như vậy cả. Đây là link đề gốc, của bên AOPS (đảm bảo chính xác!!!):

VMO 1995: https://www.artofpro...tional_olympiad

VMO 1996: https://www.artofpro...tional_olympiad

P/s: Tìm link gốc cho vui

Một cách tiếp cận khác, nhẹ nhàng hơn cho câu 6 c):

Đặt $J=DI\cap EF,S=BN\cap CM$. Kẻ đường thẳng vuông góc với $IL$, cắt $EF$ tại $X$, $DP$ tại $Y$. Dễ thấy $D,S,I,J$ thẳng hàng. Theo định lý Pascal, $B,N,K,S$ thẳng hàng, tương tự với $C,M,L,S$. Hơn nữa, theo bổ đề hình thang, $S$ là trung điểm $JD$, theo định lý con bướm $LX=LY$. Vậy $XY//JD\Rightarrow XY\bot BC$, tức là $IL//BC\Rightarrow K,I,L$ thẳng hàng $(đpcm)$.

Câu 3:

Mình giải quyết như sau:

Đặt $X=(K)\cap BC,Y=(L)\cap BC$.

$\angle INB=\angle IMC=90^0-\frac{\angle BAC}{2}$ (do $AMN$ cân tại $A$),

$\angle NIB=\angle AMN-\angle NBI=90^0-\frac{\angle BAC}{2}-\frac{\angle ABC}{2}=\frac{\angle ACB}{2}=\angle ICX$. Vậy $\Delta NIB$ và $\Delta MCI$ đồng dạng, suy ra $\frac{IB}{IC}=\frac{IN}{CM}=\frac{BN}{IM}$, suy ra $\frac {IB^2}{IC^2}=\frac{BN}{CM}$ (Do $IM=IN$). Ngoài ra ta cũng dễ cm được hai tam giác $IFN$ và $EIM$ cũng đồng dạng, suy ra $\angle FIN=\angle EIM$ và $\frac{IE^2}{IF^2}=\frac{EM}{FN}\Rightarrow \frac{IB}{IC}=\frac{IF}{IE}(*)$.

Đến đây, ta lại có $\angle FYB=\angle FIB=\angle FIN+\angle NIB=\angle IEM+\angle ICM=\angle IXY+\angle IXE=\angle EXY$

$\Rightarrow EX||FY\Rightarrow I,L,K$ thẳng hàng.

b) Câu này ta sẽ cm $BYFQ, CXEP$ là các hình thang cân, suy ra $BY=FQ,XC=PE$. Kết hợp với $BY=XC$ sẽ có ngay $đpcm$.

Thật vậy, dễ thấy $KL$ là trục $đx$ của hình thang $FYXE$ suy ra nó là hình thang cân, tới đây dễ suy ra $BYFQ, CXEP$ là các hình thang cân. 

Ta gọi $T$ là giao điểm của tiếp tuyến chung trong của $(K), (L)$ với $BC$. Thế thì $TY.TB=TX.TC$. Ta có (dễ cm được) các cặp tam giác sau đồng dạng: $TIY,IBF$ và $TIX,ICE$. từ đó ta có các kết quả sau:

$\frac{TI}{IB}=\frac{TY}{IF}, \frac{TI}{IC}=\frac{TX}{IE}$,
$\Rightarrow \frac{IB}{IC}=\frac{TY.IF}{TX.IE}$, kết hợp với $(*)$ suy ra $TY=TX\Rightarrow BY=CX\Rightarrow FQ=EP (đpcm)$.

Câu 4: Mình làm như thế này:

Ta thấy rằng $2016=2^5.3^2.7$, mà $3^2.7=1+2(1+2(1+2(1+2(1+2.1))))$, vậy nên nếu $a_k=1$ là một số hạng của dãy thì 

$a_{2k}=2a_k+1=3$

$a_{4k}=2a_{2k}+1=7$

...

$a_{2^5.k}=63$
$a_{2(2^5.k+1)-1}=63.2$

...

$a_{2^5.(2^5.k+1)-1}=63.2^5=2016$.

Nếu ta cm được có vô hạn số hạng $a_{k}=1$ của dãy, thì như vậy, tồn tại vô hạn số hạng $a_{2^5(2^5.k+1)-1}$ tương ứng có giá trị $2016$.

Thật vậy, ta để ý rằng có vô hạn số hạng $0$ trong dãy vì từ số hạng một $a_i=0$ ta có được $a_{2i+1}=2a_i=0$, dẫn tới tồn tại một dãy vô hạn các số $0$. Điều này xảy ra nếu ta chọn $i=1$. Chú ý rằng dãy trên gồm toàn các số hạng có chỉ số lẻ, nên từ đẳng thức $a_{2n}=a_{2n+1}+1$, ta suy ra tồn tại một dãy con vô hạn của dãy đầu gồm toàn các số $1$, suy $đpcm$.

P/s: Vì là từ phép suy luận ngược, dựa vào công thức truy hồi của dãy nên có lẽ công thức trên cho ta tất cả các số hạng $2016$ của dãy. (?) Khi đó câu thứ hai có thể giải quyết khá dễ dàng, chỉ số nhỏ nhất đó là $2^5(2.2^5+1)-1=2079$.

Tạp chí Mathematical Excalibur của Hong Kong với bài viết về định lý Zsigmondy và ứng dụng trong giải các bài toán khó.

Link: https://www.math.ust.hk/excalibur/v16_n4.pdf

Tìm số tự nhiên n sao cho $(n+1)^7-n^7-1$ là số chính phương

 

Capture.PNG

ta có thể xem bảng như hình vẽ trên với $1$ ở ô $(i,j)$(hàng $i$ cột $j$) nghĩa là $i\in A_j$

$d(x)$ là số tập hợp mà phần tử $x$ có mặt

ta dễ thấy vài nhận xét sau(dễ chứng minh)

$\bullet \sum_{i=1}^{1000}d(i)=\sum_{j=1}^{5}\left | A_j \right |=2500$

$\bullet \sum_{i=1}^{1000}d^2(i)=\sum_{j\neq k}\left | A_j\cap A_k \right |=\sum \left | A_j \right |+2\sum_{j<k}\left | A_j\cap A_k \right |$

$\bullet \sum_{i=1}^{1000}d^2(i)\geq 2^2.500+3^2.500=6500$

$\Rightarrow \sum_{j<k}\left | A_j\cap A_k \right |=\frac{\sum_{i=1}^{1000}d(i)^2-\sum \left | A_j \right |}{2}\geq \frac{6500-2500}{2}=2000$

ở đây ta có $n=\max\left \{ i,j\in \left \{ 1,..,5 \right \}|min\left | A_i\cap A_j \right | \right \}$ do đó ta có điều sau

$C_5^2.n\geq 2000\Rightarrow n\ge 200$

 

Hình như cm này còn thiếu phần cm n=200 thỏa mãn thì phải. bạn có thể chỉ ra một cách lập bảng thỏa mãn ycbt cho n=200 ko?

Bài 16 (IMOSL 1995):

Trong một cuộc họp, có $12k$ người tham gia, mỗi người bắt tay với đúng $3k+6$ người khác. Biết rằng với  bất kì một cách chọn cặp 2 người ta có số người bắt tay với cả 2 là như nhau. Hỏi có bao nhiêu người trong cuộc họp đó?

Cho tập $X=\{1,2,3,...1000\}$. Tìm số tự nhiên $n$ lớn nhất sao cho với 5 tập con bất kì chứa 500 phần tử $A_1, A_2, A_3, A_4, A_5$ của $X$, luôn tồn tại $1\le i,j \le 5$ mà $|A_i \cap A_j|\ge n$.