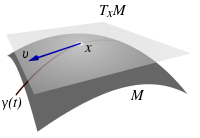
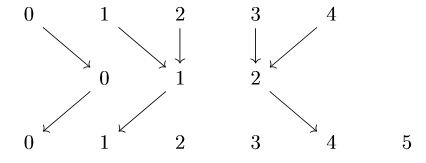
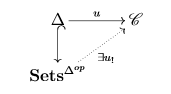
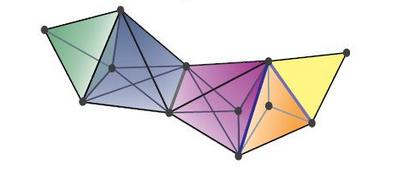
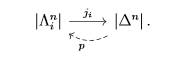
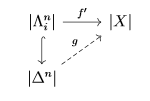Anh cũng cần 4 operations (thực ra cái anh đã làm có một bước xây dựng left adjoint cho hàm tử $Lf^*$), nhưng thực ra chả tính đối đồng điều bao giờ. Tuy nhiên, mình cứ đăng lên thôi, coi như xây dựng một môi trường văn hoá cho diễn đàn. Như anh thấy mọi người ở Pháp hay nói toán học còn có culture nữa (anh bị nói vậy khi anh nói nhiều công việc ở khoa thừa thãi không có ích cho nghiên cứu =)) ). Ví dụ như ở chỗ anh mọi người rất thích la cà với nhau, mặc dù anh cũng chưa cảm được lắm.

Thế là anh không bắt nhịp bọn này rồi, bọn Pháp cứ phải chém gió giữa giờ, giờ học, giờ ăn, cả lúc đi về. Hồi năm ba em học lý thuyết Galois ở trường, thầy (you know who) bảo lớp em học chả khác gì bọn Pháp, đại khái là hay đi muộn, tài tử, lại còn hay chém gió. Không như bọn Đức, làm cái gì chuẩn chỉ, đúng giờ, trưa nghỉ còn không hút thuốc uống cafe. Chả biết có phải em bị ngấm cái thói đấy vào máu không, nhưng giờ làm gì ngày cũng phải hai cốc cafe chém gió, ngắm trời đất chém gió toán (nếu có bạn) xong mới làm việc được.

Thực ra nếu anh nói vô ích thì nhiều thứ vô ích mà, còn chuyện người P-Đ kể cho vui miệng tý thôi. Ngay cả việc làm nhiều hội thảo hội nghị cũng có thể nói là không có ích cho nghiên cứu chứ đừng nói viết la cà trên mạng.

Em viết một là vì khi rảnh hai là vì trước đây thi thoảng em cũng đi đọc trên mạng thấy vài chỗ có ích nên mình viết mà ai đọc được một vài chi tiết thấy hay hay đã tốt rồi. Đi hội nghị, hội thảo cũng thế.

Em cũng biết một ông ở khoa làm về rigid space và có dùng vài cái của Ayoub nhưng cụ thể thế nào không rõ. Vấn đề còn tùy thuộc vào $2$-hàm tử mà mình dùng vì có một số tính chất cái này có cái kia không.

Em luận án tốt nghiệp là làm về giả thuyết Weil về số Tawagawa đó anh https://toanqpham.gi...io/Tamagawa.pdf

Cho xin template phát Toàn ơi .

Em vào trường này thì đang định xin học về chương trình Langlands ạ. Trường đại học ở Úc em học có nhiều người làm trong mảng lý thuyết biểu diễn ((geometric) representation theory) nên hồi đó em cũng cố theo học mảng này. Nói thế thôi ạ chứ em cũng quèn lắm, cũng chỉ có kiến thức mỗi mảng một ít, chưa cố đi chuyên sâu vào cái nào cả. 

 

Giờ em cũng chỉ đang cố đọc hiểu bài của Bằng với anh nxb viết ạ. Rồi nếu mà thấy thạo toán bằng tiếng việt một tí nữa thì em sẽ xin viết một bài ạ. 

Chương trình Langlands thì làm sao mà quèn được hả Toàn ? Diễn đàn mình cũng còn một anh nữa làm về Langlands hay sao, nhưng mình không tiện nhắc tên vì lâu cũng không liên lạc.

 

Thực ra cậu cứ viết bằng tiếng Anh cũng được, nhân đây em nghĩ ở mục toán hiện đại anh em có thể sử dụng hai ngôn ngữ vì đi vào nghiên cứu sâu có rất nhiều thuật ngữ không được dịch, chưa kể dùng tiếng Anh hay Việt cũng tùy gu từng người và nếu đã từng nghiên cứu dù là ở mức undergrad thì ít nhất cũng phải đọc được tiếng Anh.

Anh tự nhiên thấy dịch là “bó gai” rất hợp (lúc này “perversity” sẽ dịch là “gai”), nhưng không biết mọi người nghĩ sao.
Một câu hỏi toán học: anh đoán monoidal structure của constructible derived category phải cảm sinh một monoidal structure trên phạm trù các bó perverse (cơ chế của cái cảm sinh này có trong Higher Algebra của Lurie, mình có thể trình bày kỹ hơn trong câu trả lời khác), nhưng mà dường như cấu trúc này không có ích lợi gì? Không biết ấn tượng này có đúng không.

Ban đầu lúc nghĩ ra đối đồng điều giao thì MacPherson và Goresky muốn đặt nó là "obstinate" do nảy sinh một sự cố là một số đối chu trình cứ nhất quyết không chịu giao hoành nhau. Nhưng từ obstinate không hợp lý theo ngôn ngữ của họ, nên họ để tạm là perverse rồi định đổi tên sau, cơ mà chưa kịp đổi tên thì đã nổi tiếng sau bài báo của Bernstein, Beilinson, Deligne.

Theo em biết thì không có cái monoidal structure nào được cảm sinh cả, bó perverse chỉ ổn định dưới tác động của đối ngẫu Verdier thôi.

Về vấn đề này tôi cũng không rành lắm, nhưng nếu bạn nào có cơ duyên thì có thể trao đổi thêm với GS. Lê Tự Quốc Thắng, chắc sẽ có được thêm nhiều thông tin hữu ích.

Nói cái gì đấy bạn?

Một bó bướng bỉnh... là gì?

 

Bởi Mark Andrea de Cataldo và Luca Migliorini

 

Các đa tạp được định nghĩa bằng cách dán các tập con mở của không gian Euclide. Các dạng vi phân, các trường vector, vân vân, được định nghĩa một cách địa phương và sau đó được dán để sinh ra một đối tượng toàn cục. Khái niệm bó là hiện thân của ý tưởng dán. Các bó được sinh ra theo nhiều cách: các bó của các dạng vi phân, của các trường vector, của các toán tử vi phân, các bó hằng và hằng địa phương, vân vân. Một bó hằng địa phương (một hệ địa phương) trên một không gian $X$ được xác định bởi đơn đạo của nó, i.e., bởi một biểu diễn của nhóm cơ bản $\pi_1(X,x)$ trong nhóm các tự đẳng cấu của thớ tại $x \in X$: bó của các định hướng trên dải Möbius gán $-\operatorname{Id}$ tới các phần tử sinh của nhóm cơ bản $\mathbb{Z}$. Một bó, hoặc thâm chí một cấu xạ giữa các bó, có thể được dán lại từ dữ liệu địa phương của nó: đạo hàm ngoài có thể xem như một cấu xạ giữa các bó của các dạng vi phân; việc dán là khả thi bởi vì đạo hàm ngoài độc lập với việc chọn các toạ độ địa phương.

Lý thuyết bó được hoàn thiện hơn bằng các xét các phức của các bó. Một phức của các bó $K$ là một họ các bó $\left \{K^i \right \}_{i \in \mathbb{Z}}$ và các cấu xạ $d^i: K^i \longrightarrow K^{i+1}$ thoả mãn $d^2 = 0$. Bó đối đồng điều thứ $i$ $\mathcal{H}^i(K)$ là $\operatorname{Ker} d^i/ \operatorname{Im}  d^{i+1}$. (Bó hoá của) Phức de Rham $\mathcal{E}$ là phức với các thành phần là các bó $\mathcal{E}^i$ của các $i$-dạng vi phân và các vi phân $d^i: \mathcal{E}^i \longrightarrow \mathcal{E}^{i+1}$ được cho bởi đaọ hàm ngoài của các dạng vi phân. Bằng bổ đề Poincaré, các bó đối đồng điều đều bằng không, ngoại trừ $\mathcal{H}^0 \simeq \mathbb{C}$, bó hằng.

Định lý de Rham, phát biểu rằng đối đồng điều của một bó hằng bằng với các dạng đóng modulo các dạng khớp, dẫn tới việc rằng $\mathbb{C}$ và $\mathcal{E}$ là không thể phân biệt một cách đối đồng điều với nhau, thậm chí tại mức địa phương. Nhu cầu đồng nhất hai phức chứa thông tin đối đồng điều giống nhau thông qua một đẳng cấu dẫn tới khái niệm của phạm trù dẫn xuất: các vật là các phức và các mũi tên được thiết kế để đạt được các sự đồng nhất như mong muốn. Phép nhúng các phức $\mathbb{C} \subseteq \mathcal{E}$ được thăng hạng theo sắc lệnh lên một đẳng cấu trong phạm trù dẫn xuất bởi vì nó cảm sinh một đẳng cấu ở mức của các bó đối đồng điều.

Trong khi phạm trù dẫn xuất đưa vào một lớp dày sự trừu tượng, nó mở rộng phạm vi và tính linh hoạt của lý thuyết. Ta định nghĩa các nhóm đối đồng điều của một phức và thác triển các toán tử thông thường của tô-pô đại số lên các phức của các bó: các kéo lùi, các đẩy xuôi, các tích cup và cap, vân vân. Cũng có một phiên bản tổng quát cho đối ngẫu của các phức, tổng quát hoá đối ngẫu Poincaré cổ điển.

Các bó bướng bỉnh tồn tại trên các không gian có kì dị: các không gian giải tích, các đa tạp đại số, các không gian PL, các giả-đa tạp, vân vân. Để dễ dàng trình bày, chúng ta hạn chế xuống các bó của các không gian vector trên các đa tạp đại số phức và xuống các bó bướng bỉnh liên quan đến cái được gọi là tính bướng trung tâm (tạm dịch từ middle perversity). Để tránh đụng đến các nghịch lý như các bó được định giá trên tập Cantor, chúng ta áp đặt thêm một điều kiện kĩ thuật được gọi là tính khả dựng (tạm dịch từ constructibility). Nhắc lại rằng phạm trù $D_X$ của các phức khả dựng bị chặn của các bó trên $X$ nằm trong phạm trù dẫn xuất và ổn định dưới nhiều toán tử tô-pô vừa nhắc tới ở trên. Nếu $K$ nằm trong $D_X$, chỉ một số hữu hạn các bó đối đồng điều của nó khác không và, với mọi $i$, tập hợp $\mathrm{supp} \ \mathcal{H}^i(K)$, bao đóng của tập các điểm mà tại đó thớ là khác không, là một đa tạp đại số con.

Một bó bướng bỉnh trên $X$ là một phức khả dựng bị chặn $P \in D_X$ sao cho điều kiện sau thoả mãn với $K = P$ và đối ngẫu của nó $P^{\vee}$:
\begin{equation} \dim_{\mathbb{C}} \mathrm{supp} \ \mathcal{H}^{-i}(K) \leq i, \ \ \ \forall \ i \in \mathbb{Z}.\end{equation} Một cấu xạ giữa các bó bướng bỉnh là một mũi tên trong $D_X$.

Thuật ngữ "bó" xuất phát từ sự thật rằng, cũng giống như trong trường hợp các bó thông thường, (các cấu xạ giữa) các bó bước bỉnh có thể được dán; không giống như "bướng bỉnh", xem bên dưới. Lý thuyết của các bó bướng bỉnh có nguồn gốc trong hai khái niệm là đối đồng điều giao và $\mathcal{D}$-module. Như chúng ta thấy bên dưới, các bó bướng bỉnh và các $\mathcal{D}$-module được kết nối bởi tương ứng Riemann-Hilbert.

Giờ là thời điểm cho các ví dụ. Nếu $X$ không có kì dị, thì $\mathbb{C}_X[\dim X]$, i.e., bó hằng tại bậc $-\dim_{\mathbb{C}}X$, là tự-đối ngẫu và bướng bỉnh. Nếu $Y \subseteq X$ là một đa tạp con đóng không kì dị, thì $\mathbb{C}_Y[\dim Y]$, xem như một phức trên $X$, là một bó bướng bỉnh trên $X$. Nếu $X$ có kì dị, thì $\mathbb{C}_X[\dim X]$ thường không là một bó bướng bỉnh. Mặt khác, phức đối đồng điều giao (xem bên dưới) là một bó bướng bỉnh, bất kể $X$ có kì dị hay không. Mở rộng của hai bó bướng bỉnh là một bó bướng bỉnh. Ví dụ sau có thể đóng vai trò như một trường hợp thử cho những định nghĩa đầu tiên trong lý thuyết của các $\mathcal{D}$-module. Lấy $X = \mathbb{C}$ là đường thẳng phức với gốc $\mathfrak{o} \in X$, gọi $z$ là toạ độ chỉnh hình chuẩn, gọi $\mathcal{O}_X$ là bó các hàm chỉnh hình trên $X$, gọi $a$ là một số phức, và gọi $D$ là toán tử vi phân $D:f \longmapsto zf - af'$. Phức $P_a$
\begin{equation} \label{eq:2}
    0 \longrightarrow P^{-1}_a \coloneqq \mathcal{O}_X \overset{D}{\longrightarrow} P_a^0 \coloneqq \mathcal{O}_X \longrightarrow 0
\end{equation}
là bướng bỉnh. Nếu $a \in \mathbb{Z}^{\geq 0}$, khi đó $\mathcal{H}^{-1}(P_a) = \mathbb{C}_X$ và $\mathcal{H}^0(P_a) = \mathbb{C}_0$. Nếu $a \in \mathbb{Z}^{<0}$, khi đó $\mathcal{H}^{-1}(P_a)$ là mở rộng bởi không tại $\mathfrak{o}$ của bó $\mathbb{C}_{X \setminus \mathfrak{o}}$ và $\mathcal{H}^0(P_a) = 0$. Nếu $a \notin \mathbb{Z}$, khi đó $\mathcal{H}^{-1}(P_a)$ là mở rộng bởi không tại $\mathfrak{o}$ của hệ địa phương trên $X\setminus \mathfrak{o}$ được gán với các nhánh của hàm đa trị $z^a$ và $\mathcal{H}^0(P_a)=0$. Trong mỗi trường hợp, đơn đạo tương ứng gửi phần tử sinh theo hướng dương của $\pi_1(X \setminus \mathfrak{o},1)$ tới $e^{2\pi i a}$. Đối ngẫu của $P_a$ là $P_{-a}$ (điều này tương thích tốt với các khái niệm về liên hợp của  toán tử vi phân và đối ngẫu của các $\mathcal{D}$-module). Mỗi $P_a$ là mở rộng của bó bướng bỉnh $\mathcal{H}^0(P_a)[0]$ bởi bó bướng bỉnh $\mathcal{H}^{-1}(P_a)[1]$. Mở rộng là tầm thường (tổng trực tiếp) khi và chỉ khi $a \notin \mathbb{Z}$.

Một hệ địa phương trên một đa tạp không kì dị có thể biến thành một bó bướng bỉnh bằng cách xem nó như một phức với một thành phần duy nhất tại bậc hợp lý. Mặt khác, một bó bướng bỉnh hạn chế xuống một hệ địa phương trên một đa tạp con mở trù mật. Chúng ta muốn hiểu rõ khẩu hiệu sau: các bó bướng bỉnh là phiên bản kì dị của các hệ địa phương. Để làm vậy, chúng ta bàn tới hai ý tưởng tưởng phổ biến dẫn đến sự khai sinh của các bó bướng bỉnh vào khoảng ba mươi năm trước:tương ứng Riemann-Hilbert suy rộng (RH) và đối đồng điều giao (IH).

 

(RH) Vấn đề thứ 21 của Hilbert liên quan đến những phương trình vi phân kiểu-Fuchs trên một diện Riemann thủng $\Sigma$. Khi ta chạy quanh các vết thủng, các nghiệm bị biến đổi: bó của các nghiệm là một hệ địa phương trên $\Sigma$.

 

Vấn đề thứ 21 hỏi liệu rằng có phải mọi hệ địa phương đều được sinh ra theo cách này (nó thực sự sinh ra theo cách này). Bó hóa của các phương trình vi phân đạo hàm riêng tuyến tính trên một đa tạp dẫn đến khai niệm của $\mathcal{D}$-module. Một $\mathcal{D}$-module chính quy holonomic trên một đa tạp phức $M$ là một mở rộng của các phương trình kiểu Fuchs trên $\Sigma$. Bó của các nghiệm bây giờ được thay thế bởi phức của các nghiệm, cái mà, rất ấn tượng, thuộc vào $D_M$. Trong \ref{eq:2}, phức của các nghiệm là $P_a$, bó của các nghiệm của $D(f)=0$ là $\mathcal{H}^{-1}(P_a)$, và $\mathcal{H}^0(P_a)$ liên quan tới tính (không) giải được của $D(f)=g$. Gọi $\mathcal{D}^b_{r,h}(M)$ là phạm trù dẫn xuất bị chặn của các $\mathcal{D}$-module trên $M$ với dối đồng điều là chính quy holonomic. RH phát biểu rằng phép gán (đối ngẫu của) phức của các nghiệm cảm sinh ra một tương đương phạm trù $\mathcal{D}^b_{r,h}(M) \simeq  D_M$. Các bó bướng bỉnh bước vào trung tâm của sân khấu: chúng tương ứng với, thông qua RH, các $\mathcal{D}$-module chính quy holonomic (xem như các phức tập trung tại bậc không).

 

Để thấy sự tương ứng với khẩu hiệu được nhắc đến bên trên, phạm trù của các bó bướng bỉnh có chung các tính chất hình thức sau với phạm trù các hệ địa phương: nó là Abel (các hạt nhân, đối hạt nhân, các ảnh và các đối ảnh tồn tại, và đối ảnh đẳng cấu với ảnh), ổn định dưới tác động của đối ngẫu, Noether (điều kiện xích tăng thỏa mãn), và Artin (điều kiện xích giảm thỏa mãn), i.e., mọi bó bướng bỉnh là một mở rộng liên tiếp hữu hạn lần của các bó bưởng bỉnh đơn (không vật con). Trong ví dụ của chúng ta, các bó bướng bỉnh \ref{eq:2} là đơn khi và chỉ khi $a \in \mathbb{C} \setminus \mathbb{Z}$.

 

Các bó bướng bỉnh đơn là gì? Đối đồng điều giao cho ta câu trả lời.

 

(IH) Các nhóm đối đồng điều giao của một đa tạp kì dị $X$ với các hệ số trong một hệ địa phương là một bất biến đại số của đa tạp đó. Chúng trùng với đối đồng điều thông thường khi $X$ không kì dị và các hệ số là hằng. Các nhóm này ban đầu được định nghĩa và nghiên cứu bằng cách sử dụng lý thuyết của các xích hình học với mục đích nghiên cứu thiếu sót, do sự hiện diện của các kì dị, của đối ngẫu Poincaré cho đồng điều thông thường, và để đưa ra một biện pháp khắc phục cho nó bằng cách xét lý thuyết đồng điều sinh ra bởi việc chỉ xét các xích mà giao với tập kì dị theo cách kiểm soát được. Trong ngữ cảnh này, những dãy số nguyên nhất định, gọi là các sự bướng bỉnh (perversities), được đưa ra để cho một phép đo rằng một xích giao với tập kì dị như thế nào, do đó mà có thuật ngữ "bướng bỉnh". Các nhóm đối đồng điều giao vừa được định nghĩa thỏa mãn các kết luận của đối ngẫu Poincaré và của định lý siêu phẳng Lefschetz.

 

Mặt khác, các nhóm đối đồng điều giao còn có thể được xem như các nhóm đồi đồng điều của một số phức nhất định trong $D_M$: các phức giao của $X$ với các hệ số trong hệ địa phương. Đó là một bước ngoặt đáng chú ý trong cốt truyện của câu chuyện này khi các bó bướng bỉnh đơn chính là các phức giao của các đa tạp con bất khả quy của $X$ với các hệ số được cho bởi các hệ địa phương đơn!

Giờ chúng ta ở chỗ phải làm rõ khẩu hiệu ban đầu. Một hệ địa phương $L$ trên một đa tạp con $Z \subset M$ sinh một $\mathcal{D}$-module chính quy holonomic được định giá trên bao đóng $\overline{Z}$. Cùng $L$ đó cho ta một phức giao của $\overline{Z}$ with các hệ số trong $L$. Cả hai đối tượng mở rộng $L$ từ $Z$ lên $\overline{Z}$ theo các kì dị $\overline{Z}\setminus Z$. Bằng RH, phức giao chính là phức của các nghiệm của $\mathcal{D}$-module này.

 

Một vai trò trụ cột trong ứng dụng của lý thuyết của các bó bướng bỉnh được thể hiện bởi định lý phân rã: cho $f: X \longrightarrow Y$ là một cấu xạ riêng của các đa tạp; khi đó các nhóm đối đồng giao của $X$ với các hệ số trong một hệ địa phương đơn đẳng cấu với tổng trực tiếp của một họ các nhóm đối đồng giao của các đa tạp đại số con của $Y$, với hệ số trong các hệ địa phương đơn. Ví dụ, nếu $f: X\longrightarrow Y$ là một giải kì dị của $Y$, khi đó các nhóm đối đồng điều giao của $Y$ là một tổng trực tiếp của các nhóm đối đồng điều thông thường của $X$. Tính chẻ ra "đơn giản-nhất-có thể" này là một sự thật sâu sắc nhất được biết đến kết nối đồng điều của các đa tạp đại số phức và các cấu xạ. Nó sai trong hình học giải tích và trong hình học đại số thực. Sự phân rã của các nhóm đối đồng điều giao của $X$ là phản ảnh trong đối đồng điều của một phân rã mịn hơn của các phức trong $D_Y$. Chứng minh ban đầu của sử dụng hình học đại số trên các trường hữu hạn (các bó bưởng bỉnh hoàn toàn có nghĩa trong nhánh này).

Một ứng dụng nổi bật của vòng tròn những ý tưởng này là sự thật rằng các nhóm đối đồng điều giao của các đa tạp (varieties) xạ ảnh có cùng các tính chất cổ điển với các nhóm đối đối đồng điều của các đa tạp (manifolds) xạ ảnh: định lý $(p,q)$-phân rã Hodge, định lý Lefschetz mạnh, và quan hệ Hodge-Riemann song tuyến tính. Điều này, chắc chắn, cùng với đối ngẫu Poincaré và định lý siêu phẳng Lefschetz bên trên.

 

Những ứng dụng của lý thuyết của các bó bướng bỉnh bao quát từ hình học tới tổ hợp tới giải tích đại số. Những ứng dụng ấn tượng nhất nằm trong địa hạt của lý thuyết biểu diễn, nơi mà sự hiện diện của chúng đã dẫn tới một cuộc cách mạng thực sự ngoạn mục: những chứng minh của giả thuyết Kazhdan-Lusztig, của hình học hóa của đẳng cấu Satake, và, gần đây, của bồ đề cơ bản trong chương trình Langlands.

 

Dịch bởi Phạm Khoa Bằng.

Với Weinstein–Aronszajn identity, có được $\det\left ( 1+ A^{T}A \right )= \det\left ( 1+ AA^{T} \right )$.
Tiếp theo bởi Singular value decomposition, lại có được $A= U\Sigma V^{T}, A^{T}= V\Sigma^{T}U^{T}$,
$\Rightarrow 1+ A^{T}A= V\left ( \Sigma\Sigma^{T}+ 1 \right )V^{T}, 1+ AA^{T}= U\left ( \Sigma\Sigma^{T}+ 1 \right )U^{T}$ ($V$ unitary, $\det\left ( VW \right )= \det\left ( WV \right )= \det W$).
Lời giải bài toán Least-squares không phải duy nhất ($\det\left ( AA^{T} \right )= 0$), vì $\det\left ( 1+ AA^{T} \right )= \det\left ( 1+ A^{T}A \right )= \det\left ( 1+ \Sigma\Sigma^{T} \right )$.

Thú thật là mình không hiểu bạn viết gì, bạn cứ ném một đống link vào rồi bắt người ta đọc, đã thế còn không giải thích thêm gì, không giới thiệu thuật ngữ đấy là còn chưa nói tới việc những kiến thức bạn sử dụng là quá nhiều để giải một bài toán như thế này nên thậm chí nó có đúng, đấy là một lời giải tệ.

 

Lời khuyên, tập viết các chứng minh đơn giản và ngay ngắn trước khi cứ đi lượm link trên stack.

Em không thạo về đối đồng điều nhóm lắm nhưng vẫn xin đóng góp một post xem như mục phụ nên em sẽ không đánh số để tránh làm đứt mạch bài của mọi người.

 

Xuống thang Galois và mở rộng định lý Hilbert 90

 

Trước tiên ta nhắc lại phiên bản cổ điển của định lý Hilbert 90 với mở rộng đơn sinh.

 

Định lý 1 (Hilbert 90). Cho $\Omega/k$ là một mở rộng trường, đơn sinh với nhóm Galois $G = \left \langle \sigma \right \rangle$, nếu $\mathrm{Nm}_{\Omega/k}(\alpha)=1$ thì $\alpha = \beta/\sigma\beta$. 

 

Ví dụ 2. Mở rộng bậc hai $\mathbb{Q}(i)/\mathbb{Q}$ có nhóm Galois là $\mathbb{Z}/2$ với phần tử không tầm thường là liên hợp $\sigma: a+bi \mapsto a-bi$, chuẩn của một phần tử $a+bi$ là $a^2+b^2$. Như vậy một phần tử có chuẩn $1$ là nghiệm hữu tỷ của phương trình $a^2+b^2=1$. Định lý Hilbert 90 nói rằng tất cả các nghiệm như vậy có dạng 

$$\frac{c+di}{c-di} = \frac{c^2-d^2}{c^2+d^2} + \frac{2cd}{c^2+d^2}i.$$ Ở đây chúng ta muốn phát biểu lại dưới ngôn ngữ đối đồng điều

 

Định lý 3 (Hilbert 90). Cho $\Omega/k$ là một mở rộng Galois hữu hạn với nhóm Galois $G$ (không nhất thiết đơn sinh), khi đó $H^1(G,\Omega^{\times}) = 1.$

 

Định lý 4. Cho $\Omega/k$ là một mở rộng Galois (có thể vô hạn, tuy nhiên ở đây ta chỉ làm với trường hợp hữu hạn) với nhóm Galois $G$, khi đó $$H^1(G,\mathrm{GL}(n,\Omega))=1.$$ Nói riêng, $H^1(\mathrm{Gal}(k^{sep}/k), \mathrm{GL}(n,k^{sep}))=1$ trong đó $k^{sep}$ là bao tách được của $k$.

 

Trước tiên ta cần một số định nghĩa

 

Định nghĩa 5. Cho $\Omega/k$ là một mở rộng Galois, $U$ là một $\Omega$-không gian vector phải với một tác động $\bullet$ của $G=\mathrm{Gal}(\Omega/k)$ lên $U$. Ta nói $G$ tác động bằng các tự đẳng cấu nửa tuyến tính lên $U$ nếu

$$\sigma \bullet (u+ u') = \sigma \bullet u + \sigma \bullet u', \ \sigma \bullet (u\lambda) = (\sigma \bullet u)(\sigma \lambda),$$ trong đó $\sigma \in G, u,u' \in U, \lambda \in \Omega$. Ở đây viết $\sigma \lambda$ là tác động tự nhiên của $G$ lên $\Omega$.

 

Mệnh đề 6 (xuống thang Galois). Cho $U$ là một $\Omega$-kgvt sao cho tồn tại một tác động của $G$ lên $U$ bởi các tự đẳng cấu nửa tuyến tính thì

$$U^G = \left \{u \in U \mid \sigma \bullet u = u \ \forall \ \sigma \in G \right \}$$ là một $k$-kgvt và ta có một đẳng cấu 

$$f: U^G \otimes_k \Omega \to U, u \otimes \lambda \mapsto u\lambda$$ của các $\Omega$-kgvt.

 

Chứng minh. Trước tiên, $U^G$ là $k$-kgvt và $f$ là $\Omega$-tuyến tính là hiển nhiên. Ta chứng minh $f$ toàn ánh. Đặt

$$G = \left \{\sigma_1 = \mathrm{id},\sigma_2,...,\sigma_n \right \}.$$ Lấy $u \in U$ và $\left \{\lambda_1,...,\lambda_n \right \}$ là một $k$-cơ sở của $\Omega$. Đặt

$$u_i = \sum_j \sigma_j \bullet (u \lambda_i).$$ Ta lần lượt tác động $\sigma_k$

$$\sigma_k \bullet u_i = \sum (\sigma_k \sigma_k)\bullet (u\lambda_i).$$ Như vậy tác động này chỉ làm giao hoán các vị trí của tổng, nói cách khác $\sigma_k \bullet u_i = u_i$ và $u_i \in U^G$. Do $\sigma_1,...,\sigma_n$ là các phần tử phân biệt trong $G$ nên chúng là $k$-độc lập tuyến tính (bổ đề Dedekind) trong $\mathrm{End}_k(\Omega)$. Ma trận $M = (\sigma_i \lambda_j)_{ij}$ do đó nằm trong $\mathrm{GL}(n,\Omega)$. Lại theo định nghĩa của tác động nửa tuyến tính

$$u_i = \sum \sigma_j \bullet (u \lambda_i) = \sum (\sigma_j \bullet u)(\sigma_j \lambda_i)$$ nên nếu gọi $M^{-1} = (m_{ij})$ thì từ phương trình $M^{-1}M = I$ ta suy ra

$$\sum m_{1j}(\sigma_k \lambda_j) = \delta_{1k} \ \forall \ k =\overline{1,n}$$ trong đó $\delta_{1k}$ là ký hiệu Kronecker. Như vậy

$$\sum_j u_j m_{1j} = \sum_j \sum_k (\sigma_k \bullet u)(\sigma_k \lambda_j)m_{1j} = \sum_k (\sigma_k \bullet u)\delta_{1k} = \sigma_1 \bullet u = u.$$ Nói cách khác, $f(\sum_j u_j \otimes m_{1j}) = u$. Ta cần chứng minh nốt tính đơn ánh của $f$, để làm vậy ta chứng minh rằng nếu $u_1,...,u_r \in U^G$ là $k$-độc lập tuyến tính thì chúng vẫn là $\Omega$-độc lập tuyến tính. Giả sử tồn tại một phụ thuộc tuyến tính

$$u_1 \mu_1 + ... + u_r \mu_r = 0, \ \mu_i \in \Omega.$$ Giả sử thêm $r>1$ là số nhỏ nhất như vậy và $\mu_1 = 1$. Bằng phản chứng ta có thể giả sử không phải tất cả $\mu_i$ nằm trong $k$, ví dụ $\mu_2 \notin k$, chọn $\sigma \in G$ mà $\sigma \mu_2 \neq \mu_2$ (do $\Omega^G = k$ vì đây là mở rộng Galois). Ta có

$$\sigma \bullet (\sum_i u_i \mu_i) = \sum (\sigma \bullet u_i)(\sigma \mu_i) = \sum u_i (\sigma \mu_i) = 0.$$ Lấy phương trình này trừ cho $\sum u_i \mu_i$ ta suy ra $\sum_{i \geq 2} u_i(\sigma \mu_i - \mu_i) = 0$ ta thu được $r$ nhỏ hơn, vô lý, như vậy ta có đpcm.

 

Chứng minh định lý 4. Lấy $\alpha \in Z^1(G,\mathrm{GL}(n,\Omega))$, ta định nghĩa một tác động bởi các tự đẳng cấu nửa tuyến tính trên $\Omega^n = U$ bởi

$$\sigma \bullet u = \alpha(\sigma)(\sigma u) \ \forall \ u \in U, \sigma \in G.$$ Ở đây $\alpha: G \to \mathrm{GL}(n,\Omega)$ nên $\alpha(\sigma) \in \mathrm{GL}(n,\Omega)$ có thể tác động lên $\sigma u \in \Omega^n$. Lấy $v_1,...,v_n$ là một $k$-cơ sở của $U^G$ và cũng là một $\Omega$-cơ sở của $U$, đặt $P = (v_1 | v_2 |... | v_n) \in \mathrm{GL}(n,\Omega)$, khi đó

$$\sigma P = (\sigma v_1 | ... | \sigma v_n),$$ và 

$$v_i = \sigma \bullet v_i = \alpha(\sigma)(\sigma v_i) \ \forall \ i = \overline{1,n}.$$ Viết lại dưới dạng ma trận ta có $P = \alpha(\sigma)(\sigma P)$; nói cách khác, $\alpha$ cohomologous với đối chu trình tầm thường và ta có đpcm.

 

Hệ quả 7. $H^1(G, \mathrm{SL}(n,\Omega)) = 1$. 

Chứng minh. Xét dãy khớp

$$1 \to \mathrm{SL}(n,\Omega) \to \mathrm{GL}(n,\Omega) \overset{\mathrm{det}}{\rightarrow} \Omega^{\times} \to 1.$$ Dãy này cảm sinh ra dãy

$$H^0(G,\mathrm{GL}(n,\Omega)) \overset{\mathrm{det}}{\rightarrow} H^0(G,\Omega^{\times}) \to H^1(G, \mathrm{SL}(n,\Omega)) \to 1.$$

Tuy nhiên, $\mathrm{det}$ là toàn cấu nên $H^1(G,\mathrm{SL}(n,\Omega))=1$.

 

Định Hilbert 90 có thể mở rộng lên lược đồ

 

Định lý 8 (Hilbert 90). Tồn tại một đẳng cấu chính tắc

$$H^1_{et}(X,(\mathbb{G}_m)_X) \cong \mathrm{Pic}(X) = H^1(X,\mathcal{O}_X^{\times}),$$ trong đó $X$ là một lược đồ và $(\mathbb{G}_m)_X$ là bó nhân tính trên etale site $X_{et}$. 

 

Ý tưởng. Tồn tại cấu xạ nhúng $\epsilon: X_{Zar} \to X_{et}$ của các topo Grothendieck, ở đây $et$ là etale site và $Zar$ là topo Zariski. Như vậy theo dãy phổ Grothendieck ta có 

$$E^{p,q}_2 = H^p_{Zar}(X, R^q\epsilon^s(\mathbb{G}_m))_X \Rightarrow H^{p+q}_{et}(X, (\mathbb{G}_m)_X).$$ Trong đó $\epsilon^s(\mathbb{G}_m) = \mathcal{O}_X^{\times}$ nên đẳng cấu trong định lý Hilbert 90 thực chất là chứng minh cấu xạ edge của dãy phổ 

$$E^{1,0}_2 \overset{\cong}{\rightarrow} E^1 \Leftrightarrow H^1_{Zar}(X,\mathcal{O}^{\times})  \overset{\cong}{\rightarrow} H^1_{et}(X,(\mathbb{G}_m)_X).$$ Điều này thực chất nói rằng dẫn xuất $R^1\epsilon^s(\mathbb{G}_m)_X=0$. Ta không đi chi tiết thêm vào chứng minh.

 

Tham khảo

 

[1] G. Berhuy, An Introduction to Galois Cohomology and Its Applications.

[2] G. Tamme, Introduction to Étale Cohomology.

[3] J. P. Serre, Local Fields.

Theo sách giáo khoa thì $\int f(x)dx$ là kí hiệu cho họ nguyện hàm của $f(x)$ chứng không nói gì về $dx$ cả.

Nhưng trong các bài toán thì em thấy $dx$ nhưng đang nhân với $f(x)$ VD: $\int \frac{dx}{\sqrt{x+1}}$.

Anh chị có thể giải thích $dx$ nó thật sự là kí hiệu hay là đang nhân với $f(x)$ trong $\int f(x)dx$ ạ ?

Em cảm ơn.

Kiến thức trong SGK thực chất chưa cho phép giải thích bản chất của cách viết $f(x)dx$ và $\int f(x)dx$. Kí hiệu $dx$ là một ví dụ của cái gọi là $1$-dạng vi phân.

 

Hãy lấy ví dụ một không gian (bạn chưa cần hiểu không gian là gì) $M$ mà tại mỗi điểm của $x \in M$ ta có thể lấy một không gian tiếp xúc (tangent space) $T_x M$, một phần tử (hay vector) của $T_xM$ gọi là một vector tiếp xúc với $M$ tại $x$. Hợp của các không gian tiếp xúc $\bigcup_{x \in X} T_xM$ gọi phân thớ tiếp xúc của không gian $M$.

 

 

Ví dụ ở trên mặt phẳng $M = \mathbb{R}^2$, thì mỗi vector tiếp xúc tại một điểm $(a,b)$ chỉ là một vector có điểm xuất phát là $(a,b)$ và tất cả các mặt phẳng tiếp xúc đều trùng nhau, chỉ khác điểm xuất phát.

 

Khi đó một $1$-dạng vi phân $\alpha$ là một cách gán cho mỗi điểm $x \in M$ một ánh xạ tuyến tính (bạn cũng chưa cần biết nó là gì, cứ hiểu là một dạng hàm)

 

$$\alpha: TM \longrightarrow \mathbb{R} \Rightarrow \alpha_x = \alpha_{\mid T_x M}: T_x M \longrightarrow \mathbb{R}$$

 

Nói cách khác, một $1$-dạng vi phân là một cái gì đó mà ta có thể tính giá trị trên các vector tiếp xúc. Kí hiệu $f(x)dx$ là một $1$-dạng vi phân trên $\mathbb{R}$ (nói là kí hiệu, vì còn tuỳ vào miền xác định của hàm $f$). Đặc biệt hơn hàm $f(x)$ có thể xem là một $0$-dạng vi phân, và ta có thể nhân $0$-dạng với $1$-dạng. Nói cách khác, viết $f(x).dx$ là nhân $0$-dạng với $1$-dạng. Còn để hiểu $dx$ bạn cần xem nó như hàm

$$dx: T_{x_0}\mathbb{R} \longrightarrow \mathbb{R}$$

gán mỗi vector tiếp xúc với $x_0 \in \mathbb{R}$ với một giá trị. Cụ thể hơn nếu ta chọn một hướng dương cho $\mathbb{R}$ thì một vector tiếp xúc tại $x_0$ chỉ là một điểm bên phải hoặc bên trái $x_0$ trên $\mathbb{R}$, khi đó $dx$ xác định duy nhất bởi điều kiện $dx(\mathbf{v})=1$ với $\mathbf{v}$ là vector đơn vị xuất phát từ $x$ theo hướng dương. Tất cả các vector tiếp xúc khác có dạng $a\mathbf{v}$ với $a \in \mathbb{R}$ và ta có $dx(a\mathbf{v})=a$.

 

Tổng quát hơn, trong $\mathbb{R}^n$ thì $1$-dạng vi phân sẽ có dạng

$$f_1(x_1,...,x_n)dx_1 + \cdots + f_n(x_1,...,x_n)dx_n,$$

và tổng quát hơn nữa ta có $k$ dạng vi phân

$$\sum_{1 \leq i_1 < \cdots < i_k \leq n} f_{i_1,...i_k}(x_1,...,x_n)dx_{i_1}\cdots dx_{i_k}.$$

Với không gian $n$-chiều $M$ thì ta có thể tích phân các $n$-dạng vi phân (tức là các dạng với nhiều số biến nhất). Do đó ví dụ trong $\mathbb{R}^1$ bạn có tích phân $\int_a^b f(x)dx$ trong khi trong $\mathbb{R}^2$ bạn lại tích phân $\int_{(a,b)\times(c,d)} f(x,y)dxdy$.

Hôm qua đọc được cái blog này nên thả vào đây cho mọi người, level rất phổ thông và cũng rất hay vì đã bàn được cái local-to-global principle và nhóm Brauer. Một người mù tịt lý thuyết số nuhw mình đọc cũng hiểu.

Định lý Ostrowski cho trường số

 

Định ly Ostrowski cho $\mathbb{Q}$ nói rằng mọi chốn của $\mathbb{Q}$ chính xác tới một tương đương là các định giá $p$-adic và giá trị tuyệt đối. Ta có thể mở rộng định lý Ostrowski cho trường số. Cho $K$ là một trường số (một mở rộng hữu hạn của $\mathbb{Q}$), ký hiệu $\mathcal{O}_K$ là bao đóng nguyên của $\mathbb{Z}$ trong $K$. Ta biết rằng $\mathcal{O}_K$ là một miền Dedekind, tức là: miền Noether, đóng nguyên (integrally closed), chiều Krull một và quan trọng hơn mọi ideal có phân tích duy nhất thành tích các ideal nguyên tố. Ký hiệu $\mathfrak{p}$ bởi một ideal nguyên tố của $\mathcal{O}_K$. Định lý Ostrowski khi này nói mọi giả trị tuyệt đối trên $K$ đến từ bậc triệt tiêu của một ideal nguyên tố của $\mathcal{O}_K$ hoặc là hạn chế của giá trị tuyệt đối của một phép nhúng thực hoặc phức của $K$.

 

Định nghĩa. Với $x \in \mathcal{O}_K \setminus 0$, ta định nghĩa $\mathrm{ord}_{\mathfrak{p}}(x) = m$ nếu $(x) = x\mathcal{O}_K = \mathfrak{p}^m\mathfrak{a}$ trong đó $m \geq 0$ và $\mathfrak{p} \nmid \mathfrak{a}$. (một tính chất khác của miền Dedekind: quan hệ bao hàm tương đương quan hệ chia hết trên lớp các ideal).

 

Không khó để mở rộng định nghĩa này lên $K^{\times}$ bằng cách định nghĩa $\mathrm{ord}_{\mathfrak{p}}(x/y) = \mathrm{ord}_{\mathfrak{p}}(x) - \mathrm{ord}_{\mathfrak{p}}(y)$ ($x,y \in \mathcal{O}_K \setminus 0$). Ta có thể kiểm tra $\mathrm{ord}_{\mathfrak{p}}(x+y) \geq \min\left \{\mathrm{ord}_{\mathfrak{p}}(x),\mathrm{ord}_{\mathfrak{p}}(y) \right \}$.

 

Định nghĩa. Với $c \in (0,1)$ ta định nghĩa $\left |\alpha \right|_{\mathfrak{p}} = c^{\mathrm{ord}_{\mathfrak{p}}(\alpha)}$ với $\alpha \in K^{\times}$ và gọi nó trị tuyệt đối $\mathfrak{p}$-adic trên $K$. Theo quy ước, ta thường gọi đây là các chốn hữu hạn của $K$. Các chốn vô hạn được định nghĩa nhờ vào các phép nhúng thực và phức của $K$. Giả sử $L$ là một trong hai trường $\mathbb{R}$ hoặc $\mathbb{C}$, khi đó mỗi nhúng $\sigma: K \longrightarrow L$ cho ta một trị tuyệt đối $\left|\alpha \right|_{\infty} = \left|\sigma(\alpha) \right|_{\infty}$ trong đó $\left |\cdot\right|_{\infty}$ vế phải là trị tuyệt đối thông thường trên $\mathbb{R}$ hoặc $\mathbb{C}$.

 

Bổ đề. Cho $\mathfrak{p}$ là một ideal nguyên tố không tầm thường của $\mathcal{O}_K$. Nếu $\alpha \in K^{\times}$ và $\mathrm{ord}_{\mathfrak{p}}(\alpha) \geq 0$ thì $\alpha = x/y$ với $x,y \in \mathcal{O}_K$ trong đó $\mathrm{ord}_{\mathfrak{p}}(y)=0$.

 

Chứng minh. Viết $\alpha \mathcal{O}_K = \mathfrak{a}\mathfrak{b}^{-1}$ với $\mathfrak{a},\mathfrak{b} \subset \mathcal{O}_K$ là các ideal (ta có thể viết $\alpha$ dưới dạng phân số và sử dụng phân tích duy nhất) sao cho không có thành phân chung trong phân tích duy nhất ra tích các ideal nguyên tố. Ta cũng có thể giả sử $\mathfrak{b}$ không chia hết $\mathfrak{p}$ do $\mathrm{ord}_{\mathfrak{p}}(\alpha) \geq 0$ và $\mathfrak{a},\mathfrak{b}$ không có nhân tử chung. Trong nhóm lớp các ideal (thương của nhóm các fractional ideal cho các principal fractional ideal) ta có $\mathfrak{a} = (\alpha)\mathfrak{b}$ nên $\mathfrak{a},\mathfrak{b}$ nằm trong cùng một lớp ideal. Gọi $\mathfrak{c}$ là một phần tử trong lớp $[\mathfrak{a}]^{-1} = [\mathfrak{b}]^{-1}$ mà nguyên tố cùng nhau với $\mathfrak{p}$. Khi đó $(\alpha) = \mathfrak{a}\mathfrak{b}^{-1}=(\mathfrak{a}\mathfrak{c})(\mathfrak{b}\mathfrak{c})^{-1}$. Hai ideal $\mathfrak{a}\mathfrak{c}$ và $\mathfrak{b}\mathfrak{c}$ đều là ideal chính nên ta có thể đặt chúng lần lượt là $(x)$ và $(y)$ với $x,y \in \mathcal{O}_K$. Do $\mathfrak{b}$ nguyên tố cùng nhau với $\mathfrak{b}$ nên $\mathrm{ord}_{\mathfrak{p}}(y) =0$. Như vậy $(\alpha)=(x/y)$. Thay $x$ bởi $ux$ với $u$ là đơn vị nếu cần thiết, ta có $\alpha=x/y$ với $\mathrm{ord}_{\mathfrak{p}}(y)=0$.

 

Mệnh đề. Giả sử $v: K^{\times} \longrightarrow \mathbb{R}$ là một đồng cấu không tầm thường sao cho $v(\alpha+\beta) \geq \min \left \{v(\alpha),v(\beta) \right\}$ trong đó $\alpha,\beta,\alpha+\beta \in K^{\times}$. Khi đó $v = t\mathrm{ord}_{\mathfrak{p}}$ với $t>0$ và $\mathfrak{p}$ là một ideal nguyên tố của $\mathcal{O}_K$ (cả hai đều xác định duy nhất).

 

Chứng minh. Tính duy nhất khá hiển nhiên. Ví dụ tính duy nhất của $\mathfrak{p}$ do

$$\mathfrak{p} = \left \{\alpha \in \mathcal{O}_K \mid \alpha \in \mathfrak{p} \right \} = \left \{\alpha \in \mathcal{O}_K \mid \mathrm{ord}_{\mathfrak{p}}(\alpha)>0 \right \} = \left \{\alpha \in \mathcal{O}_K \mid t\mathrm{ord}_{\mathfrak{p}}(\alpha)>0 \right \}.$$ Trong đó tính duy nhất của $t$ suy ra từ việc việc $t$ là giá trị dương nhỏ nhất mà $t\mathrm{ord}_{\mathfrak{p}}$ lấy trên $K^{\times}$.

 

Giờ ta chứng minh sự tồn tại, giả sử ta có $v$, khi đó xét

$$\mathfrak{p} = \left \{\alpha \in \mathcal{O}_K \setminus 0 \mid v(\alpha) > 0 \right \} \cup \left \{0\right \}.$$

Trước khi chứng minh $\mathfrak{p}$ là ideal nguyên tố của $\mathcal{O}_K$, ta sẽ chứng minh $v$ lấy giá trị không âm trên toàn $\mathcal{O}_K \setminus 0$. Thật vậy $v(1) = v(1.1) = v(1) + v(1)$ nên $v(1)=0$. Do đó ta cũng có $0=v(1)=v(-1)+v(-1)$ nên $v(-1)$. Từ bất đẳng phức phi archimedean ta suy ra $v(a) \geq 0$ với mọi $a \in \mathbb{Z}$. Giờ giả sử $\alpha \in \mathcal{O}_K$, ta chọn $n$ nhỏ nhất có thể sao cho tồn tại một quan hệ

$$\alpha^n + a_{n-1}\alpha^{n-1} + \cdots + a_1 \alpha + a_0=0,$$

trong đó $a_j \in \mathbb{Z}$. Do tính nhỏ nhất của $n$, $a_0 \neq 0$. Viết lại phương trình cho ta $\alpha^n = -a_{n-1}\alpha^{n-1}-\cdots -a_0$. Giờ ta phản chứng giả sử $v(\alpha) < 0$. Ta chỉ xét tới $a_j \neq 0$, khi đó $v(-\alpha_j \alpha^{n-1}) = v(a_j) + jv(\alpha) \geq jv(\alpha) \geq (n-1)v(\alpha)$ (do $j \neq n-1$ và $v(\alpha)<0$). Sử dụng bất đẳng thức phi archimedean ta thấy

$$nv(\alpha) = v(\alpha^n) = v(LHS) = v(RHS) \geq (n-1)v(\alpha) \Rightarrow v(\alpha)\geq 0,$$

điều này trái với giả thiết phản chứng nên $v(\alpha) \geq 0$. Ta thấy $v$ không thể đồng nhất $0$ trên $\mathcal{O}_K \setminus 0$ vì nếu vậy nó sẽ tầm thường trên $K^{\times}$, trái giả thiết, nên $v$ phải lấy một giá trị dương nào đó trên $\mathcal{O}^{\times}$. Do đó $\mathfrak{p} \neq 0$. Do $v$ là một đồng cấu nên $\mathfrak{p}$ là một nhóm con của $\mathcal{O}_K$. Do tính không âm của $v$ trên $\mathcal{O}_K \setminus 0$ nên ta thấy $\mathfrak{p}$ là một ideal của $\mathcal{O}_K$. Giờ ta thấy nó là ideal nguyên tố, thật vậy lấy $\alpha,\beta \in \mathcal{O}_K\setminus 0$ sao cho $\alpha \beta \in \mathfrak{p}$, khi đó một trong hai $v(\alpha),v(\beta)$ phải dương cho $v(\alpha)+v(\beta) = v(\alpha \beta) > 0$. Bây giờ ta sẽ chứng minh $v = t\mathrm{ord}_{\mathfrak{p}}$. Trước tiên ta phải chứng minh $\mathrm{ord}_{\mathfrak{p}}(\alpha)=0 \Rightarrow v(\alpha)=0$. Theo bổ đề trước $\alpha=x/y$ với $\mathrm{ord}_{\mathfrak{p}}(y)=0$. Do đó $\mathrm{ord}_{\mathfrak{p}}(x) = \mathrm{ord}_{\mathfrak{p}}(\alpha y) = 0 + 0 = 0$. Như vậy cả $x,y$ không thuộc $\mathfrak{p}$. Theo định nghĩa của $\mathfrak{p}$ thì $v(x)=v(y)=0$. Do đó $v(\alpha)=v(x)-v(y) = 0$. 

 

Giờ với $\alpha \in K^{\times}$ ta viết $n =\mathrm{ord}_{\mathfrak{p}}(\alpha) \in \mathbb{Z}$. Lấy $\gamma \in \mathfrak{p} \setminus \mathfrak{p}^2$, khi đó $\mathrm{ord}_{\mathfrak{p}}(\gamma) = 1$ và $v(\gamma)>0$. Khi đó $\mathrm{ord}_{\mathfrak{p}}(\alpha/\gamma^n) = 0$ nên $v(\alpha/\gamma^n)=0$, nên

$$v(\alpha) = nv(\gamma) = \mathrm{ord}_{\mathfrak{p}}(\alpha)v(\gamma),$$

nói cách khác ta xác định được $v(\gamma)=t>0$. Cách chọn $\gamma$ không phụ thuộc $\alpha$ nên $v = t\mathrm{ord}_{\mathfrak{p}}$. Kết thúc chứng minh.

 

Giờ ta chứng minh định lý Ostrowski cho trường số.

 

Định lý (Ostrowski). Giả sử $K/\mathbb{Q}$ là một trường số, khi đó mọi trị tuyệt đối không tầm thường trên $K$ tương đương hoặc với một trị tuyệt đối $\mathfrak{p}$-adic với $\mathfrak{p}$ là một ideal nguyên tố của $\mathcal{O}_K$ hoặc một trị tuyệt đối đến từ một phép nhúng thực hoặc phức của $K$.

 

Chứng minh. Giả sử $\left | \cdot\right|$ là trị tuyệt đối trên $K$. Nếu $\left| \cdot \right|$ là phi archimedean thì hàm $v(\alpha) = -\log \left|\alpha \right|$ thoả mãn điều kiện của định lý trước. Do đó $-\log \left| \cdot \right| = t \mathrm{ord}_{\mathfrak{p}}$ nên $\left | \cdot \right | = (e^{-t})^{\mathrm{ord}_{\mathfrak{p}}(\cdot)}$ (lưu ý $e^{-t} \in (0,1)$).

 

Trường hợp khó hơn là nếu $\left |\cdot \right|$ là archimedean, ta sẽ chứng minh tồn tại một nhúng $\sigma$ của $K$ vào $\mathbb{R}$ hoặc $\mathbb{C}$. Trước tiên ta hạn chế $\left |\cdot \right|$ xuống $\mathbb{Q}$, khi đó nó vẫn archimedean (một trị tuyệt đối trên $K$ là phi archimedean khi và chỉ khi $\left |n \right| \leq 1$ với mọi $n \in \mathbb{Z}$) và do đó $\left |r \right| = \left |r \right|_{\infty}^t$ với $t >0, r \in \mathbb{Q}$. Ký hiệu $\hat{K}$ là một đầy đủ hoá (completion) của $K$ ứng với chuẩn $\left |\cdot \right|$. Ký hiệu $\hat{\mathbb{Q}}$ là bao đóng của $\mathbb{Q}$ trong $\hat{K}$. Khi đó $(\hat{\mathbb{Q}},\left| \cdot \right|)$ và $(\mathbb{R},\left|\cdot \right|^t_{\infty})$ là hai đầy đủ hoá của $(\mathbb{Q},\left| \cdot\right|)$ nên chúng phải đẳng cấu dưới tư cách hai trường định giá, ký hiệu một đẳng cấu $\sigma: \hat{\mathbb{Q}} \longrightarrow \mathbb{R}$ là một đẳng cấu như vậy. Khi đó $\left|x \right|  = \left|\sigma(x)\right|^t_{\infty}$ với mọi $x \in \hat{\mathbb{Q}}$.

 

Theo định lý phần tử nguyên thuỷ ($\mathbb{Q}$ có đặc số $0$ nên luôn áp dụng được) $K = \mathbb{Q}(\gamma)$ với $\gamma \in K$ nào đó. Nếu $\gamma \in \hat{\mathbb{Q}}$ ta suy ra $K \subset \hat{\mathbb{Q}}$ và $\left |\alpha \right| = \left |\sigma(\alpha) \right|_{\infty}^t$ với mọi $\alpha \in K$. Điều này chứng tỏ $K$ được nhúng thực. Hơn nữa, vì $\hat{\mathbb{Q}}$ chứa $K$ nên $\hat{\mathbb{Q}}$ trù mật trong $\hat{K}$; tuy nhiên bản thân $\hat{\mathbb{Q}}$ đầy đủ nên $\hat{K}=\hat{\mathbb{Q}} = \mathbb{R}$, chứng tỏ rằng $K \hookrightarrow \hat{K}$ là một phép nhúng thực.

 

Trường hợp $\gamma \notin \hat{\mathbb{Q}}$ khi đó $\hat{\mathbb{Q}}(y)$ là một mở rộng hữu hạn của $\hat{\mathbb{Q}}$ (do $K/\mathbb{Q} = \hat{\mathbb{Q}}/\mathbb{Q}$ là hữu hạn) với $[\hat{\mathbb{Q}}(y):\hat{\mathbb{Q}}] > 1$. Do $\mathbb{C}$ đóng đại số và $[\mathbb{C}:\mathbb{R}]=2$ nên mở rộng đại số duy nhất của $\mathbb{R}$ là $\mathbb{R}$ hoặc $\mathbb{C}$. Do đó $[\hat{\mathbb{Q}}(\gamma):\hat{\mathbb{Q}}]=2$ và ta có hai cách mở rộng $\sigma:\hat{\mathbb{Q}} \longrightarrow \mathbb{R}$ lên thành $\tau: \hat{\mathbb{Q}}(y) \longrightarrow \mathbb{C}$. Cố định một mở rộng $\tau$ như vậy. Do $\hat{\mathbb{Q}}(\gamma)/\hat{\mathbb{Q}}$ hữu hạn và $\hat{\mathbb{Q}}$ đầy đủ với tô-pô sinh bởi $\left | \cdot \right|$ nên $\hat{\mathbb{Q}}(\gamma)$ cũng đầy đủ với tô-pô sinh bởi $\left |\cdot \right|$. Ta có $K=\mathbb{Q}(\gamma) \subset \hat{\mathbb{Q}}(\gamma) \subset \hat{K}$, lập luận tương tự trường hợp trước ta thấy $\hat{\mathbb{Q}}(\gamma)=\hat{K}$. Nói cách khác $\hat{K} \simeq \mathbb{C}$, chứng tỏ rằng $K$ được nhúng phức.

Hàm tử phức chuẩn hóa và phần suy biến

 

Bắt chước cách làm của phức kì dị của một không gian tôpô ta định nghĩa khái niệm phức Moore.

 

Định nghĩa 9. Phức Moore $M$ là một hàm tử $M: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ biến mỗi vật đơn hình $A$ thành một phức (cùng kí hiệu) $A$ mà vị trí thứ $n$ là $A_n$ và vi phân

$$d = d_0 - d_1 + ... + (-1)^n d_n: A_n \to A_{n-1}.$$

Một thủ tục đơn giản cho ta thấy $d^2=0$. 

 

Câu hỏi. $M: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ có phải là một phần trong tương đương ta mong muốn không?

 

Trả lời. Không. Cụ thể hơn, nếu $M$ là một phần của tương đương, thì nó phải toàn ánh trên lớp các vật, nói riêng, phải tồn tại một vật đơn hình $A$ mà $MA$ là phức

$$ ... \to 0 \to 0 \to \mathbb{Z} (\text{vị trí 0}) \to 0.$$

Do đó $A_0 = \mathbb{Z},A_1 = 0$, tuy nhiên nhắc lại rằng $s_j$ là đơn cấu nên $A_0 \hookrightarrow A_1$, điều này vô lý. 

 

Lý do xảy ra điều này là vi phân của phức Moore quá phức tạp và quá dư thông tin trong từng thành phần $A_n$, ta sẽ thu nhỏ $M$ để đạt được tương đương mong muốn. 

 

Định nghĩa 10. Hàm tử phức chuẩn hóa $N: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ biến mỗi vật đơn hình $A$ thành phức $N$ mà

$$(NA)_n = \bigcap_{i=1}^n \mathrm{Ker}(d_i:A_n \to A_{n-1}) \ \forall n > 0, \ (NA)_0 = A_0.$$

Dễ thấy $(NA)_{\bullet}$ là một phức với vi phân $d_0$ (do trong vi phân $d$ của phức Moore triệt tiêu hết $d_1,...,d_n$). Đồng điều của phức chuẩn hóa được gọi là nhóm đồng luân của vật đơn hình, kí hiệu

$$\pi_n(A) = H_n(NA).$$

 

Ví dụ 11. $N\mathbb{Z}\Delta[0]$ chính là phức $ ... \to 0 \to 0 \to \mathbb{Z} (\text{vị trí 0}) \to 0$, do đó khẳng định phức chuẩn hóa là tốt hơn phức Moore. 

 

Chúng ta trước tiên sẽ chứng minh hai tính chất của hàm tử phức chuẩn hóa: nó loại bỏ tất cả phần "suy biến" trong một vật đơn hình, nó là hàm tử trung thành, đầy đủ. 

 

Định nghĩa 12. Phần suy biến được định nghĩa bởi $(DA)_n = \sum_{i=0}^n s_i(X_{n-1})$. 

 

Bổ đề 13. $(NA)_n \cap (DA)_n = 0$. 

 

Chứng minh. Lấy $x \in (NA)_n \cap (DA)_n$, khi đó tồn tại số $i$ lớn nhất mà 

$$x = s_i(a_i) + \cdots + s_n(a_n), \ a_j \in X_{n-1}.$$

Nếu $i = n$ thì $0 = d_n x = d_n s_n (a_n) = 0 \Rightarrow x = s_n(a_n) = 0$. Trong trường hợp $i \leq n-1$ ta tác động $d_i$ vào hai vế thu được

\begin{align*} 0  = d_i x & = a_i + d_i s_{i+1}(a_{i+1}) \cdots + d_i s_n (a_n) \\ & = a_i + s_i d_i(a_{i+1}) + \cdots + s_{n-1}d_i(a_n). \end{align*} Hệ quả là 

\begin{align*} x & = s_i\left(s_i d_i(-a_{i+1})  + \cdots + s_{n-1}d_i(a_n) \right) + s_{i+1}(a_{i+1}) + \cdots + d_i s_n(a_n) \\ & = s_{i+1}s_id_i(-a_{i+1}) + \cdots s_n s_i d_i(a_n) + s_{i+1}(a_{i+1}) + \cdots + s_n(a_n) \\ & = s_{i+1}(a_{i+1}-s_id_i(a_{i+1})) + ... + s_n(a_n - s_i d_i(a_n)), \end{align*} điều này trái với giả thuyết về $i$.

 

Bổ đề 14. $(NA)_n + (DA)_n = A_n$. 

 

Chứng minh. Đặt các nhóm con $P_n^k = \left \{x \in A_n \mid d_i x = 0 \ \forall i > k \right \}$ 

$$(NA)_n = P^0_n \subset P^1_n \subset ... \subset P^n_n = A_n.$$

Ta sẽ chứng minh bằng quy nạp rằng $P^i_n + D_n = A_n$ bằng quy nạp lùi. Khi $i=n$ thì hiển nhiên, giả sử khẳng định đúng với $i=k$, ta chứng minh nó đúng với $i=k-1$. Lấy $a \in A_n$ ta giả sử viết được $a = b + c$ với $b \in P^k_n, c \in D_n$, khi đó có thể kiểm tra

$$a = (b - s_{k-1}d_kb) + (c + s_{k-1}d_k b)$$ trong đó có thể kiểm tra $b-s_{k-1}d_k b \in P^{k-1}_n$ và $c + s_{k-1}d_k b \in D_n$. 

 

Bổ đề 15. Đồng luân của một nhóm abel đơn hình đẳng cấu với đồng điều của chính nó 

$$\pi_n(A) \cong H_n(MA).$$

Chứng minh. Ta chỉ cần chứng minh $D=DA$ là acyclic. Ta lọc $DA$ bởi

$$F_i D_n  = \begin{cases} 0 & i = 0, \\ D_n & n \leq p, \\ s_0(A_{n-1}) + \cdots + s_p(A_{n-1}) &  \text{trường hợp khác}. \end{cases}$$ Hiển nhiên lọc này bị chặn nên ta có một dãy phổ

$$ E^1_{p,q} = H_{p+q}(F_pD/F_{p-1}D) \Rightarrow_{p+q=n} H_{p+q}(D).$$

Hệ quả là ta cũng chỉ cần chứng minh $F_pD/F_{p-1}D$ là một phức acyclic, ta có thể xây dựng một toán tử đồng luân tầm thường $\sigma: (F_pD/F_{p-1}D)_n \to (F_pD/F_{p-1}D)_{n+1}$ thỏa mãn

$$\mathrm{id} = \sigma \left( \sum (-1)^i d_i \right) + \left(\sum (-1)^i d_i \right) \sigma.$$

Cụ thể ta tìm được $\sigma_n = (-1)^{p+1}s_p$. Đây chỉ là kiểm tra trực tiếp với các đẳng thức đơn hình, lưu ý mỗi phần tử của

$$(F_pD/F_{p-1}D)_n = \frac{s_0(A_{n-1}) + \cdots + s_{p-1}(A_{n-1}) + s_p(A_{n-1})}{s_0(A_{n-1}) + \cdots + s_{p-1}(A_{n-1})}$$ đều có dạng $s_p(\text{smth})$.

Phạm trù số

 

Định nghĩa 1. $\Delta$ là phạm trù mà các vật là các tập sắp thứ tự toàn phần $[n] = (0 \leq 1 \leq ... \leq n)$, các cấu xạ là các ánh xạ bảo toàn thứ tự $\alpha: [m] \to [n]$, điều này có nghĩa $\alpha(i) \leq \alpha(j)$ nếu $i \leq j$.  Một đơn cấu (tương ứng, toàn cấu) trong $\Delta$ được định là ánh xạ bảo toàn thứ tự và là đơn ánh trên tập hợp (tương ứng, toàn ánh).

 

Định nghĩa 2. Đối mặt là các cấu xạ $d^i: [n-1] \to [n]$, $0 \leq i \leq n$ cho bởi
\begin{equation}
    d^i(k) = \begin{cases}
        k, & k < i\\
        k+1, & k \geq i+1
    \end{cases}
\end{equation}
Về ý nghĩa, các cấu xạ $d^i$ là các đơn cấu duy nhất $[n-1] \to [n]$, nó khuyết phần tử $i \in [n]$. Các cấu xạ $s^i: [n+1] \to [n], 0 \leq i \leq n$ cho bởi
\begin{equation}
    s^i(k) = \begin{cases}
        k, & k < i \\
        k-1, & k \geq i+1
    \end{cases}
\end{equation}
là các toàn cấu duy nhất $[n+1] \to [n]$, chúng được gọi là các đối suy biến. $s^i$ lặp phần tử $i \in [n]$ hai lần.

 

Định lý 3. Mọi cấu xạ $\alpha: [m] \to [n]$ có thể viết thành hợp một số đối mặt và một số đối suy biến.

 

Chứng minh. Ta chứng minh bằng quy nạp theo $n$. Nếu $n=0$ thì $\alpha$ hoặc là ánh xạ đồng nhất hoặc là hợp một số đối mặt. Giả sử khẳng định đúng tới $n$ và $\alpha: [n+1] \to [m]$ là một cấu xạ. Nếu $\alpha$ là đơn cấu thì $\alpha$ là hợp một số đối mặt. Nếu $\alpha$ không là đơn cấu thì tồn tại $k \in [n+1]$ mà $\alpha(k) = \alpha(k+1)$ (lưu ý điều này không xảy ra với một ánh xạ tổng quát mà chỉ đúng khi $\alpha$ bảo toàn thứ tự). Xét cấu xạ $\alpha':[n] \to [m]$ xác định bởi $\alpha'(i) = \alpha(i)$ nếu $i \leq k$ và $\alpha'(i) = \alpha(i+1)$ nếu $i>k$. Khi đó $\alpha = \alpha' s^k$ và ta thu được điều phải chứng minh khi áp dụng giả thiết quy nạp cho $\alpha'$.

 

Từ định lý trên ta thấy chỉ nên hạn chế sự tập trung xuống các đối mặt và các đối suy biến. Cụ thể, ta có một loạt các đẳng thức liên hệ trong định lý dưới đây.

 

Bổ đề 4. Trong phạm trù số các đẳng thức sau, gọi là các đẳng thức đối đơn hình, thỏa mãn

\begin{matrix}
       d^j d^i = d^i d^{j - 1}  & i < j \\
       s^j d^i = d^i s^{j-1}  &  i < j\\
       s^j d^j = \mathrm{id} = s^j d^{j+1} & \\
       s^j d^i = d^{i-1} s^j & i > j+1 \\
       s^j s^i = s^i s^{j+1} & i \leq j \\
\end{matrix}

Chứng minh. Ta chỉ chứng minh đẳng thức đầu tiên, tất cả các đẳng thức còn lại chứng minh tương tự. Lấy $i < j$ và $k \in [n]$. Ta có
\begin{equation}
    d^j d^i(k) = d^j\left(\begin{cases} k, & k < i \\ k + 1, & k \geq i \end{cases} \right) =
    \begin{cases}
        k, & k < i\\
        k+1,& i \leq k, k+1 < j \\
        k+2, &j \leq k+1
    \end{cases}
\end{equation}
và
\begin{equation}
    d^i d^{j-1}(k) = d^i\left(\begin{cases} k, & k < j -1 \\ k+ 1, & k \geq j-1 \end{cases} \right) = \begin{cases}
        k, & k < i \\
        k+1, & i \leq k, k+1 < j \\
        k+2, & j \leq k+1
    \end{cases}
\end{equation}
Do đó $d^j d^i = d^i d^{j-1}$ nếu $i < j$.

 

Định lý 5 (phân tích đơn-toàn cấu). Với mọi ánh xạ bảo toàn thứ tự $\varphi: [n] \to [m]$, tồn tại và duy nhất một phân tích $\varphi = \mu \sigma$ trong đó $\mu, \sigma$ lần lượt là các toàn cấu, đơn cấu bảo toàn thứ tự.

 

Chứng minh. Trước tiên ta chứng minh sự tồn tại, gọi $i_s <...<i_1$ là các phần tử của $[m]$ không nằm trong ảnh của $\varphi$ và $j_1 < ... <j_t$ là các phần tử của $[n]$ mà $\alpha(j) = \alpha(j+1)$. Nếu $p = n-t = m-s$ thì ta có một phân tích
\begin{equation}
    [n] \overset{\sigma}{\twoheadrightarrow} [p] \overset{\mu}{\hookrightarrow} [m]
\end{equation}
trong đó $\mu=d^{i_1}...d^{i_s}$ và $\sigma = s^{j_1}...s^{j_t}$. Để minh hoạ cho chứng minh, ta xét một cấu xạ $[4] \to [5]$ được cho bởi hình sau

Như vậy tập ảnh của cấu xạ này là $(0<1<4)$, ta nhúng $(0<1<2)$ vào $[5]$ bởi $0\mapsto 0, 1 \mapsto 1, 2 \mapsto 4$ sẽ thu được phân tích  

Dễ thấy $[4] \twoheadrightarrow [2]$ và $[2] \hookrightarrow [5]$.

Bây giờ ta chứng minh tính duy nhất, lấy hai đơn cấu $\mu_i:[k_1] \to [m]$ và hai toàn cấu $\sigma:[n] \to [k_i]$ ($i = 1,2$) thỏa mãn $\varphi = \mu_1\sigma_1 = \mu_2\sigma_2$. Đếm số lượng phần tử của ảnh $\mathrm{Im}(\mu_i \sigma_i)$ ta suy ra $k_1=k_2$ và do $\mu_1,\mu_2$ là các đơn cấu với cùng tập ảnh ta suy ra $\mu_1=\mu_2=\mu$, điều này cũng suy ra $\sigma_1=\sigma_2$ do $\mu$ là đơn cấu.

Lý thuyết đồng luân trong phạm trù vật đơn hình

 

Định nghĩa 6. Một vật đơn hình trong một phạm trù $\mathscr{C}$ là một hàm tử $X: \Delta^{op} \to \mathscr{C}$. Phạm trù $s\mathscr{C}=\mathscr{C}^{\Delta^{op}}=\mathrm{Fun}(\Delta^{op},\mathscr{C})$ có vật là các vật đơn hình và cấu xạ là các biến đối tự nhiên giữa chúng. Hơn nữa ta viết, $X_n = X([n]), d_i = X(d^i)$ là mặt và $s_j = X(s^j)$ là suy biến của $X$. Nếu $\alpha$ là một cấu xạ trong $\Delta$, ta viết $X(\alpha) = X_{\alpha}$.

 

Ví dụ 7. Một tập đơn hình trong phạm trù tập hợp $\mathbf{Sets}$ được gọi là một tập đơn hình, một trong các tập đơn hình thú vị nhất là $\Delta^n= \mathrm{Hom}_{\Delta}(\square,[n]): \Delta^{op} \to \mathbf{Sets}$ - ta gọi đây là đơn hình chuẩn $n$-chiều. Theo bổ đề Yoneda ta có
\begin{equation}
    X_n = X([n]) \cong \mathrm{Hom}(\mathrm{Hom}(\square,[n]),X).
\end{equation}
Phép nhúng Yoneda
\begin{equation}
    \begin{split}
        \Delta &\hookrightarrow \mathbf{Sets}^{\Delta^{op}} \\
        [n] & \mapsto \Delta^n
    \end{split}
\end{equation}
là trung thành, đầy đủ, hơn nữa nó còn trù mật theo nghĩa nếu $\mathscr{C}$ là một phạm trù có đối giới hạn với tập chỉ số bất kỳ thì mọi hàm tử $u:\Delta \to \mathscr{C}$ đều có thể nâng lên thành một hàm tử $u_{!}:\mathbf{Sets}^{\Delta^{op}} \to \mathscr{C}$. Nói cách khác, ta có một biểu đồ giao hoán

Cụ thể với mỗi $X \in \mathrm{Obj}(\mathbf{Sets}^{\Delta^{op}})$ thì theo ta biết $X \cong \underset{\Delta^n \to X}{\mathrm{colim}} \ \Delta^n$ (chứng minh sau!) nên ta có thể định nghĩa
\begin{equation}
    u_{!}(X) = \underset{\Delta^n \to X}{\mathrm{colim}} \ u([n]).
\end{equation}
Ngược lại ta cũng có một hàm tử $u^{\star}: \mathscr{C} \to \mathbf{Sets}^{\Delta^{op}}$ là liên hợp của $u_{!}$ định nghĩa bởi
\begin{equation}
    (u^{\star}(C))_n = \mathrm{Hom}_{\mathscr{C}}(u([n]),C) \ \forall \ C \in \mathrm{Obj}(\mathscr{C}).
\end{equation}

Về sau ta sẽ thấy cặp liên hợp $(\mathrm{Sing}(\square),\left | \square \right|)$ là một hệ quả của ý tưởng vừa phân tích.

 

Bổ đề 8. Với mọi vật đơn hình $X$ thì các đẳng thức sau, gọi là các đẳng thức đơn hình, thỏa mãn

\begin{matrix}
      d_i d_j = d_{j-1} d_i & i < j\\
       d_i s_j= s_{j-1}d_i &  i < j\\
       d_j s_j = \mathrm{id} = d_{j+1}s_j & \\
       d_i s_j =  s_j d_{i-1} & i > j+1 \\
       s_i s_j = s_{j+1}s_i & i \leq j
\end{matrix}

 

Chứng minh. Hệ quả hiển nhiên của các đẳng thức đối đơn hình.

Bài viết giới thiệu về lý thuyết đơn hình (simplicial theory), một lý thuyết "tổ hợp" của tôpô đại số. Kí hiệu $\mathbf{Top},\mathbf{Sets},\mathbf{Ab}$ lần lượt là phạm trù các không gian tôpô, phạm trù các tâp hợp, phạm trù các nhóm abel.

 

Giới thiệu

H. Poincaré lần đầu định nghĩa đồng điều theo nghĩa tam giác phân một không gian và thực hiện các tính toán tổ hợp với định nghĩa này. Tuy nhiên cách định nghĩa này không hiệu quả ở điểm nó cần chứng minh các cách tam giác phân đều cho ta một nhóm đồng điều.

Tiếp đó, không phải mọi không gian đều có thể tam giác phân. Sau này, các định nghĩa trừu tượng cho phép ta hiểu một tam giác là một ánh xạ liên tục $\left |\Delta^n \right| \to X$, trong đó $\left |\Delta^n \right|^n$ định nghĩa bởi

\begin{equation} \left|\Delta^n \right|=\left \{ (x_0,...,x_n) \in \mathbb{R}^{n+1} \mid x_i \in [0,1], x_0 + \cdots + x_n = 1 \right \}.\end{equation}

Các ánh xạ này cho ta một họ
\begin{equation} \mathrm{Sing}(X)_n = \left \{ \sigma: \left|\Delta^n \right| \to X \mid \sigma \ \text{liên tục} \ \right\}. \end{equation}
Tuy nhiên các tập $\mathrm{Sing}(X)_n$ không đứng riêng lẻ do bản thân các đơn hình hình học $\left|\Delta^n \right|$ có liên hệ với nhau, ví dụ một tam giác sẽ có ba đỉnh. Ngoài ra, do tính affine ta hoàn toàn có thể đồng nhất các đơn hình hình học với các đỉnh của nó. Ví dụ $\left|\Delta^n \right|$ có $(n+1)$-đỉnh $v_0,...,v_n$ ($v_i$ có tất cả các vị trí là $0$ ngoài $1$ ở vị trí $i$) có thể đồng nhất với tập $\left \{0,1,...,n \right \}$. Như vậy một tam giác có thể xem là "tập" $\left \{0,1,2\right \}$ với ba đỉnh $\left \{0 \right \}, \left \{1\right \}, \left \{2 \right \}$ và ba cạnh $\left \{0,1\right \}, \left \{1,2\right \}, \left \{0,2\right \}$. Đây là sự xuất hiện của phạm trù $\Delta$ với vật là các tập $[n]=\left \{0,1,...,n \right \}$, nó được gọi là phạm trù số. Trong khi $\mathrm{Sing}(X)$ là một tập đơn hình theo nghĩa nó gửi mỗi $[n]$ đến $\mathrm{Sing}(X)_n$ (nó cũng là một $\infty$-phạm trù). Như vậy, tóm gọn lại ta có một quy trình
\begin{equation} X  \rightarrow (\text{phức kì dị}) \ \mathrm{Sing}(X) \rightarrow (\text{hàm tử tự do}) \ \mathbb{Z}\mathrm{Sing}(X) \rightarrow (\text{phức+ đồng điều}) \  H_{\bullet}(X).\end{equation}
Thực chất đây là một loạt các hàm tử giữa các phạm trù
\begin{equation} \mathbf{Top} \to s\mathbf{Sets} \to s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab}),\end{equation}
trong đó $s\mathbf{Sets},s\mathbf{Ab}$ lần lượt là phạm trù các tập đơn hình và phạm trù các nhóm abel đơn hình. Như vậy thực chất ta đang làm đại số đồng điều trong $\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$. Sau này ta sẽ biết rằng  $\mathrm{Sing}: \mathbf{Top} \to s\mathbf{Sets}$ có liên hợp là hàm tử hình học hóa trong khi đó định lý tương ứng Dold-Kan nói rằng $s\mathbf{Ab}$ tương đương với $\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$, như vậy bước khó khăn có lẽ nằm ở phép lấy hàm tử nhóm abel tự do.

 

Định lý tương ứng Dold-Kan là một tương đương giữa hai phạm trù các phức không âm và các vật đơn hình. Để hiểu định lý Dold-Kan do đó ta bắt buộc phải hiểu các vật đơn hình, và để hiểu các vật đơn hình ta phải hiểu phạm trù $\Delta$. Để định nghĩa phạm trù số ta sẽ định nghĩa các đối mặt và đối suy biến (ta gọi như vậy để thuận tiện thay vì gọi là phép đối mặt và phép đối suy biến). Sau đó chúng ta chứng minh các đẳng thức đối đơn hình và chứng minh mọi cấu xạ trong phạm trù số có một phân tích rất đặc biệt gọi là phân tích đơn-toàn cấu.

Lý thuyết đồng luân đơn hình: không gian Eilenberg-MacLane, không gian Moore

 

Định nghĩa 22. Với mọi $n$ và $0 \leq i \leq n$, $(n,i)$-sừng (tiếng Anh, horn) $\Lambda^n_i:\Delta^{op} \to \mathbf{Sets}$ là tập đơn hình con của $\Delta^n$ định nghĩa bởi
$$(\Lambda_i^n)([m]) = \left \{\alpha \in \mathrm{Hom}_{\Delta}([m],[n]) \mid [n] \not\subset \alpha([m]) \cup \left \{i \right \} \right \}.$$ Một cách hình học, $\Lambda^n_i$ chính là hợp của tất cả các mặt ngoại trừ mặt thứ $i$ của $\Delta^n$.

 

Định nghĩa 23. Cho $X$ là một tập đơn hình, khi đó $X$ được gọi là fibrant nếu nó thỏa mãn điều kiện Kan sau:

Với mỗi cấu xạ $f: \Lambda_i^n \to X$, tồn tại $\overline{f}: \Delta^n \to X$ làm giao hoán biểu đồ sau

Ở ngôn ngữ tập hợp nó có nghĩa là:

Với mọi $n$ và $k$ thỏa mãn $0 \leq k \leq n$, nếu $x_0,...,x_{k-1},x_{k+1},...,x_n \in X_n$ thỏa mãn $d_i x_j = d_{j-1}x_i \ \forall i < j$ và $i,j \neq k$ thì tồn tại $y \in X_{n+1}$ sao cho $d_i(y) = x_i \ \forall i \neq k$.

 

Mặc dù không sử dụng định nghĩa này, nhưng ta vẫn nhắc lại rằng một $\infty$-phạm trù là một tập đơn hình $X$ thỏa mãn điều kiện Kan với mọi $\Lambda^n_i \to X$ với mọi $0 < i < n$, trong đó $n \geq 2$.

 

Định lý 24. Cho $\mathcal{F}:\mathscr{C} \to \mathbf{Sets}$ là một tiền bó của các tập hợp, khi đó $\mathcal{F}$ luôn có thể xem là một đối giới hạn trên một phạm trù slice.

 

Hệ quả 25. Cho $X$ là một tập đơn hình khi đó $X \cong \underset{\Delta^n \to X}{\mathrm{colim}}\ \Delta^n$, trong đó đối giới hạn được lấy trong phạm trù $(\Delta \downarrow X)$.

 

Định lý 26. Với mọi tập đơn hình $X$ thì $\left|X \right|$ luôn là một CW-phức.

 

Định lý 27. Hàm tử hình học hóa $\left| \square \right|: s\mathbf{Sets} \to \mathbf{Top}$ là liên hợp trái của hàm tử phức kỳ dị $\mathrm{Sing}(\square): \mathbf{Top} \to s\mathbf{Sets}$.

 

Chứng minh. \begin{equation*}
    \begin{aligned}
        \mathrm{Hom}_{\textbf{Top}}(\left | X \right|, Y) &  \cong \mathrm{Hom}_{\textbf{Top}}(\text{colim}_{\Delta^n \to X} \left |\Delta^n \right|, Y) \\
        & \cong \lim_{(\Delta \downarrow X)} \mathrm{Hom}_{\textbf{Top}}(\left |\Delta^n \right |, Y) \\
        & \cong \lim_{(\Delta \downarrow X)} \mathrm{Hom}_{\textbf{Sets}}(\Delta^n, \text{Sing}(Y)) \\
        & \cong \mathrm{Hom}_{\textbf{Sets}}(\text{colim}_{(\Delta \downarrow X)} \Delta^n, \mathrm{Sing}(Y))  \cong \mathrm{Hom}_{\textbf{Sets}}(X, \text{Sing}(Y))
\end{aligned}
\end{equation*}
với mọi tập đơn hình $X$ và không gian tôpô $Y$ nên ta có điều phải chứng minh.

 

Định lý 27. Cho $X$ là một không gian tôpô, khi đó vật đơn hình $\mathrm{Sing}(X)$ thỏa mãn điều kiện Kan.

 

Chứng minh. Với mọi phép nhúng $j_i: \left| \Lambda_i^n \right| \hookrightarrow \left | \Delta^n \right|$ dễ thấy tồn tại một phép co rút $p: \left| \Delta^n \right| \to \left| \Lambda^n_i \right|$ theo nghĩa $p \circ j_i = \mathrm{id}$.

Ta đã định nghĩa dược hình học hóa của một tập đơn hình, một lẽ tự nhiên ta có thể định nghĩa $\pi_n(X) = \pi_n(\left|X \right|)$ với một tập đơn hình $X$. Dưới đây ta sẽ đưa ra một cách định nghĩa khác của nhóm đồng luân theo một cách hoàn toàn tổ hợp và nhóm định nghĩa được vẫn đẳng cấu với $\pi_n(\left|X\right|)$.

Tuy nhiên ta luôn có thể lấy $g = f' \circ p$.

 

Định nghĩa 28. Cho $X$ là một tập đơn hình và một điểm gốc $v \in X_0$, ta định nghĩa $\pi_n(X,v)$ như sau. Đặt
$$Z_n = \left \{ x \in X_n \mid d_i(x) = s_0^{n}(v) \forall i = \overline{0,n}  \right \}.$$ Ta nói hai phần tử $x, x'$ của $Z_n$ là đồng luân, kí hiệu $x \sim x'$, nếu tồn tại $y \in X_{n+1}$ (gọi là một đồng luân từ $x$ đến $x'$) thỏa mãn
$$d_i(y) = \begin{cases}
        s_0^{n}(v) ,&  i < n \\
        x, & i = n \\
        x,' &  i = n+1.
    \end{cases}$$

Bình luận. Trước tiên chi tiết lấy điểm gốc $v \in X_0$. Thứ nhất, ta có thể xem $X$ như một không gian tôpô và đồng thời là phức kì dị của nó $\mathrm{Sing}(X)$ khi đó một điểm gốc $v$ nên nằm trong $X = \mathrm{Sing}(X)_0$. Thứ hai, cách tạo ra điểm gốc này tạo cho ta một phạm trù mới $\mathbf{Top}_{\star}$ mà trong đó vật là các cặp $(X,v)$; khác với $\mathbf{Top}$, phạm trù này có vật $0$ là tập một phần tử. Tương tự, ta có phạm trù $s\mathbf{Sets}_{\star}$. Ta biết rằng cho $v \in X_0$ tương đương với cho
$$v \in \mathrm{Hom}_{s\mathbf{Sets}}(\Delta^0, X).$$ Một cách tự nhiên $v$ ta một phần tử trong $\mathrm{Hom}_{\mathbf{Sets}}((\Delta^0)_n,X_n)$ chính là $s^n_0(v) \in X_n$. Cuối cùng là định nghĩa của $Z_n$, ta nhắc lại định nghĩa nhóm đồng luân thông thường của một không gian tôpô $X$
$$\pi_n = \mathrm{Hom}_{\mathbf{Top}_{\star}}(S^n, X)/\simeq.$$ Theo quan điểm đơn hình, ta nên định nghĩa
$$\pi_n^{\text{đơn hình}} = \mathrm{Hom}_{s\mathbf{Sets}_{\star}}(\Delta^n/\partial \Delta^n, X)/\simeq,$$ trong đó $\partial \Delta^n = \cup d^i(\Delta^{n-1})$. Như vậy cho $\alpha \in  \mathrm{Hom}_{s\mathbf{Sets}_{\star}}(\Delta^n/\partial \Delta^n, X)$ tương đương với cho một $\alpha \in \mathrm{Hom}_{\mathbf{Sets}}(\Delta^n,X) \cong X_n$ mà

Nói cách khác, $s_0^{n}(v) = x(d^i) = d_i(x)$.

 

Bổ đề 29. Nếu $X$ là một tập đơn hình fibrant thì $\sim$ là một quan hệ tương đương.

 

Chứng minh. Quan hệ này là phản xạ do $y = s_n x$ là một đồng luân từ $x$ tới chính nó. Để thấy $\sim$ đối xứng và bắc cầu, gọi $y$ là một đồng luân từ $x$ tới $x'$ và $y'$ là một đồng luân từ $x'$ tới $x^{''}$. Điều kiện Kan áp dụng cho các phần tử $s_0^{n+1}(v),...,s_0^{n+1}(v),y,y'$ cho ta một phần tử $z \in X_{n+2}$ mà $d_{n}z = y, d_{n+1}z = y'$ và $d_iz = s_0^{n+1}(v)$ với $i < n$. Phần tử $d_{n+2}z$ do đó là một đồng luân tử $x$ đến $x^{''}$.

 

Định nghĩa 30. Cho $X$ là một tập đơn hình fibrant và một số nguyên $n \geq 1$, tập thương $Z_n/\sim$ có thể được trang bị một phép nhân khiến nó trở thành một nhóm, ta gọi đây là nhóm đồng luân của $X$, kí hiệu bởi $\pi_n(X,v)$.

 

Định lý 31. Nếu $X$ là một tập đơn hình fibrant thì cấu xạ chính tắc $\eta_X: X \to \mathrm{Sing}(\left| X \right|)$ là một đồng luân yếu. Hệ quả là $\eta_X$ cảm sinh một đẳng cấu chính tắc $\pi_n(X,x) \cong \pi_n(\left|X \right|,x)$ với mọi $n \geq 1$.

 

Định lý 32. Cho $X$ là một không gian tôpô thì cấu xạ chính tắc $j:\left| \mathrm{Sing}(X) \right| \to X$ là một đồng luân yếu. Ngoài ra nó cũng cảm sinh đẳng cấu trên tất cả các nhóm đồng điều.

 

Định nghĩa 33. Cho $X$ là một vật đơn hình trong $\mathscr{A}$, nhóm đồng luân thứ $n$ của $X$ định nghĩa bởi $\pi_n(X) = H_n(NX)$ trong đo $N$ là phức chuẩn hóa.

 

Ví dụ. Nếu $G$ là một nhóm đơn hình hoặc một môđun đơn hình với điểm gốc $v = 1$ (nhắc lại, $G$ luôn tự động là fibrant). Xét nhóm
$$N_n(G) = \left \{x \in G_n \mid d_i(x) = s_0^n(1) = 1 \ \forall \ i \neq 0 \right \}.$$ Khi đó $Z_n = \mathrm{Ker}(d_0:N_n \to N_{n-1})$ và $Z_n/\sim = Z_n/B_n$ trong đó $B_n = \left \{x \mid x \sim 1 \right\} = \mathrm{Im}(d_{n+1}:N_{n+1}\to N_n)$. Nói cách khác, $\pi_n(G,1)$ là đồng điều của phức $N_{\bullet}$
$$ ... \to N_2 \overset{d_2}{\rightarrow} N_1 \overset{d_1}{\rightarrow}N_0 \to 1.$$ Điều này giải thích tại sao định nghĩa trước là một mở rộng hợp lý.

 

Định nghĩa 34 (không gian Eilenberg-MacLane).

• Cho $G$ là một nhóm abel và $n$ là một số tự nhiên, một không gian tôpô $X$ thỏa mãn
  $$\pi_k(X)  = 0 \ \forall k \neq n, \
      \pi_n(X)  = G$$ được gọi là một không gian Eilenberg-MacLane kiểu $K(G,n)$.
• Cho $G$ là một nhóm abel và $n$ là một số tự nhiên, một tập đơn hình fibrant $K$ thỏa mãn
  $$ \pi_k(K)  = 0 \ \forall k \neq n, \
      \pi_n(K)  = G$$ được gọi là một tập đơn hình Eilenberg-MacLane kiểu $K(G,n)$.

Bổ đề 35. Cho $G$ là một nhóm abel và $n$ là một số tự nhiên, ta đồng nhất $G$ với phức $C_{\bullet}$ trong $\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ mà $C_0 = G$ và $C_i = 0$ với mọi $i \neq 0$, khi đó $KG[-n]$ là một tập đơn hình Eilenberg-MacLane kiểu $K(G,n)$.

 

Chứng minh. Rõ ràng ta chỉ cần tính nhóm đồng luân của $KG[-n]$, tuy nhiên điều này khá dễ dàng vì theo định lý Dold-Kan thì $$\pi_k(KG[-n]) = H_k(NKG[-n]) \cong H_k(G[-n]) \cong G$$ nếu $k=n$ và $\cong 0$ nếu $k \neq n$.

 

Hệ quả. $\left|KG[-n] \right|$ là một không gian Eilenberg-MacLane kiểu $K(G,n)$.

 

Định nghĩa 36. Cho $X$ là một tập đơn hình fibrant, cấu xạ $h: X \to \mathbb{Z}X$ gửi $X$ tới các phần tử trong cơ sở của $\mathbb{Z}X$ cảm sinh một đồng cấu
$$\pi_{\bullet}(X) \to \pi_{\bullet}(\mathbb{Z}X) \cong H_{\bullet}(N\mathbb{Z}X) \cong H_{\bullet}(\mathbb{Z}X)$$ (ở đây ta đã sử dụng sự kiện phép chiếu $kX \to NX$ là một tương đương đồng luân), cấu xạ cảm sinh này được gọi là đồng cấu Hurewicz.

 

Định nghĩa 37. Cho một nhóm abel $G$ và một số nguyên $n \geq 1$, một không gian Moore kiểu $M(G,n)$ là một CW-phức $X$ thỏa mãn
$$\widetilde{H}_i(X)  = 0 \ \forall \ i \neq n, \ H_n(X)  = G,$$ trong đó $\widetilde{H}$ kí hiệu nhóm đồng điều rút gọn.

 

Bổ đề 38. Với mọi nhóm abel $G$ và một số nguyên $n \geq 1$, tồn tại một không gian Moore (không nhất thiết chính xác tới một đồng luân).

Đối đồng điều của không gian Eilenberg-MacLane

 

Bài viết này bàn tới việc, tại sao (đối) đồng điều của không gian Eilenberg-MacLane lại khó tính? Ở đây ta sẽ bàn tới mô hình đơn hình (simplicial set) của không gian $K(G,n)$ - $G$ là một nhóm abel, $n \geq 0$. Nhắc lại không gian $K(G,n)$ được định nghĩa bởi

$$\pi_i(K(G,n)) = \begin{cases} G, & \ i = n \\ 0, & i \neq 0. \end{cases}$$

Trong đó $K(G,n)$ được xác định chính xác tới một đồng luân yếu và thậm chí tới một đồng luân nếu ta làm trong phạm trù các CW-phức. Câu hỏi là, tuy nhóm đồng luân của $K(G,n)$ đơn giản như vậy nhưng điều gì làm (đối) đồng điều của nó phức tạp? Trước tiên, ta quay về với mô hình "tổ hợp" của $K(G,n)$ và do đó phải nhắc tới định lý tương ứng Dold-Kan.

 

Định lý (tương ứng Dold-Kan). Cho $\mathscr{A}$ là một phạm trù abel, khi đó hàm tử phức chuẩn hóa $N$ là một tương đương phạm trù giữa $\mathbf{Ch}_{\geq 0}(\mathscr{A})$ và $s\mathscr{A}$. Trong đó $\mathbf{Ch}_{\geq 0}(\mathscr{A})$ là phạm trù các phức mà các vị trí $<0$ là tầm thường và $s\mathscr{A}$ là phạm trù các vật đơn hình trên $\mathscr{A}$; nói cách khác, phạm trù $\mathscr{A}^{\Delta^{op}}$.

 

(Phạm trù $\Delta$ đơn giản có các vật là $[n] = (0 < 1 <...<n)$ và cấu xạ là các ánh xạ bảo toàn thứ tự) Như vậy tồn tại một hàm tử nghịch đảo $K$ (biến một phức thành một vật đơn hình) của $N$, vấn đề đã trở nên đơn giản hơn, nhóm $G$ sẽ được đồng nhất với phức

$$...0 \to 0 \to ... \to 0 \to G (\text{vị trí 0}) \to 0.$$

Phức $KG[-n]$ do đó sẽ là một vật đơn hình Eilenberg-MacLane, lấy hình học hóa $|KG[-n]|$ cho ta một mô hình cụ thể của không gian Eilenberg-MacLane. Trước khi đi xa hơn, ta quay về một vấn đề đơn giản của hàm tử dẫn xuất: gọi $A$ là một vật trong phạm trù abel $\mathscr{A}$ và $T: \mathscr{A} \to \mathscr{A'}$ là một hàm tử cộng tính. Quy trình quen thuộc là lấy một giải thức xạ ảnh

$$P_{\bullet}: ... \to P_n \to ... \to P_1 \to P_0 \to A \to 0.$$

Sau đó xóa $A$ và lấy đồng điều của phức

$$TP^{del}_{\bullet}: ... \to TP_n \to ... TP_1 \to TP_0 \to 0, \ \ L_qT(A) = H_q(TP^{del}_{\bullet}).$$ Trước tiên có hai vấn đề cần lưu ý:

• Tại sao ta cần giả thiết $T0 = 0$? Đơn giản là để $TP_{\bullet}$ vẫn là một phức ($T(\text{vi phân}^2) = T0 = 0$) và do đó lấy được đồng điều; tại bước này ta không cần giả thiết cộng tính.
• Tại sao ta cần giả thiết cộng tính? Trả lời: là để hàm tử dẫn xuất định nghĩa một cách duy nhất từ bổ đề so sánh đồng luân của phức xây chuyền xạ ảnh. Một đồng luân $f-g=ds + sd$ chỉ giữa nguyên dạng khi hàm tử $T$ cộng tính.

Bây giờ câu hỏi là làm sao ta định nghĩa dẫn xuất của $T$ khi bỏ đi giả thiết cộng tính (vẫn cần $T0=0$)? Dold & Puppe trong một bài báo của họ đã định nghĩa khái niệm giải thức đơn hình xạ ảnh kiểu $(A,n)$, nó chỉ đơn giản là một vật đơn hình $X$ (trên $\mathscr{A}$) mà

$$H_n(X) \cong A, H_i(X) = 0 \ \forall \ i >n, X_i = 0 \ \forall i < n,$$

và định nghĩa dẫn xuất hai chỉ số của $T$ bởi

$$L_qT(A,n) = H_q(TX).$$

Ví dụ khi $\mathscr{A} = \mathscr{A'} = \mathbf{Ab}$ là phạm trù các nhóm abel thì ta có hai hàm tử không cộng tính

$$TA = \mathbb{Z}A \otimes G, \ \ T'A = \mathrm{Sym}(A) \otimes G,$$

trong đó $\mathbb{Z}, \mathrm{Sym}$ là hàm tử đại số nhóm và hàm tử đại số đối xứng. Khi $T$ là cộng tính thì $L_qT(A,n) \cong L_{q-n}TA$. Ký hiệu đồng điều hoặc đối đồng điều của $K(A,n)$ trong một vành giao hoán có đơn vị $R$ lần lượt bởi

$$H^*(K(A,n),R) = H^*(A,n;R), \ \ H_*(K(A,n),R) = H_*(A,n;R).$$

Định lý sau trả lời câu hỏi ban đầu của ta.

 

Định lý. (Dold&Puppe) Cả hai dẫn xuất $L_qT(A,n), L_qT'(A,n)$ đều đẳng cấu với $H_q(A,n;G)$.

 

Ý tưởng chứng minh. Hàm tử $T'$ phức tạp hơn - dựa vào công trình của Dold&Thom và Spanier về tích đối xứng vô hạn $SP^{\infty}$; trong khi hàm tử $T$ hầu như theo định nghĩa. Thật vậy

$$L_qT(A,n) = H_q(\mathbb{Z}[KG[-n]] \otimes G) = H_q(A,n; G),$$

trong đó ta đã dùng sự kiện đồng điều một vật đơn hình (ở đây là $KG[-n]$) là đồng điều của phức $\mathbb{Z}[X_{\bullet}]$ (ví dụ, đồng điều kỳ dị của không gian tô-pô $X$ là đồng điều của vật đơn hình $\mathrm{Sing}(X)$) và sự kiện đồng điều của vật đơn hình đẳng cấu với đồng điều của hình học hóa của nó.

 

Định lý của Dold&Puppe cho ta một câu trả lời: sự khó khăn trong tính toán (đối) đồng điều của không gian Eilenberg-MacLane xuất phát từ việc chúng là dẫn xuất của các hàm tử không cộng tính. Trong bài báo On the group $H(\Pi,n)$, II của MacLane, ông đã định nghĩa giải thức bar, một phức hoàn toàn đại số để tính $H_{\bullet}(A,n;G)$. Điều này là tự nhiên do ta định nghĩa $K(A,n)$ từ đối tượng đại số và đi tính một bất biến đại số của một không gian tô-pô thì tại sao không làm việc thuần túy đại số từ đầu? Giải thức bar có liên hệ chặt chẽ với dẫn xuất của $\mathrm{Sym}$, là cơ sở để MacLane định nghĩa cách đo độ cộng tính của một hàm tử + hàm tử đa thức và làm động lực cho Cartan, trong semináire Henri Cartan (1954-1955) tính toàn thành công $H_{\bullet}(A,n;G)$ với $G = \mathbb{Z}_p,\mathbb{Z}$ ($p$ là số nguyên tố) và $A$ là nhóm abel hữu hạn sinh.

 

Tuy nhiên, chứng minh của Cartan cực kỳ phức tạp; khi thành công với bài báo này người ta tin rằng tô-pô đại số có lẽ sắp kết thúc tuy nhiên sau đó họ nhận ra là cỗ máy tính này dù chỉ thay một chỉ tiết nhỏ cũng không thể tính toán được tiếp được. Duy chỉ phát biểu kết quả $H_{\bullet}(A,n,\mathbb{Z}_p)$ ($p$ nguyên tố lẻ) có lẽ cũng đã mất $2$ trang latex.

Định lý Dold-Thom

 

Trong phần này ta sẽ trình bày về tích đối xứng vô hạn, kết quả đáng lưu ý nhất trong phần này là định lý Dold-Thom nói rằng tích đối xứng vô hạn của không gian Moore chính là không gian Eilenberg-MacLane.

 

Định nghĩa 39. (Tích đối xứng vô hạn)

• Cho $X$ là một không gian tôpô với một điểm gốc $x_0 \in X$. Với mỗi $n \geq 0$ ta định nghĩa $$\mathrm{Sym}^0 X = x_0, \ \ \mathrm{Sym}^n X = X^n/ S_n \ \forall n \geq 1,$$ trong đó $X^n$ là tích Descartes $n$ lần của $X$, $X^n/S_n$ là không gian thương của $X^n$ dưới tác động của nhóm đối xứng $S_n$ bằng cách hoán đổi các vị trí. Các phép nhúng tự nhiên $\mathrm{Sym}^nX \to \mathrm{Sym}^{n+1}X$ định nghĩa bởi $(x_1,...,x_n) \mapsto (x_0,x_1,...,x_n)$. Tích đối xứng vô hạn $\mathrm{Sym}^{\infty}X$ được định nghĩa là giới hạn của dãy $$x_0 = \mathrm{Sym}^0 X \subset \mathrm{Sym}^1 X \subset \mathrm{Sym}^2X \subset ... \subset \mathrm{Sym}^nX \subset ...$$ tôpô trên $\mathrm{Sym}^{\infty}X$ được định nghĩa là tôpô yếu định nghĩa bởi họ $\left \{\mathrm{Sym}^n X \right \}$; tức là một tập $F \subset \mathrm{Sym}^{\infty}X$ là đóng khi và chỉ khi $F \cap \mathrm{Sym}^n X$ là đóng với mọi $n$.
• Cho $K$ là một tập đơn hình với một đỉnh góc $e_0 \in K_0$. Với mỗi $k > 0$ đặt $e_k = s_0^k e_0$ và định nghĩa $K(e_0)$ là vật đơn hình con của $K$ sinh bởi $e_0$ ($K(e_0)$ có đúng một $k$-đơn hình với mỗi $k \geq 0$, chính là $e_k$). Với mỗi $n \geq 0$, ta định nghĩa tích đối xứng $\mathrm{Sym}^n K$ bởi $$\mathrm{Sym}^0 K = K(e_0), \ \ \mathrm{Sym}^n K = K^n/S_n \ \forall n \geq 1,$$ trong đó $K^n$ là tích Descartes $n$ lần của $K$, $K^n/S_n$ là vật thương xác định bởi tác động của nhóm đối xứng bằng cách đổi chỗ các vị trí. Với mỗi $n \geq 1$, các $q$-đơn hình của $\mathrm{Sym}^nK$ là các bộ (không sắp thứ tự) $n$ vị trí, mỗi vị trí là một $q$-đơn hình của $K$, toán tử biên và suy biến thỏa mãn $$ d_i(\sigma_1...\sigma_n)  = (d_i \sigma_1)...(d_i\sigma_n), \ s_i(\sigma_1...\sigma_n)  = (s_i\sigma_1)...(s_i\sigma_n).$$ Ta định nghĩa một cấu xạ nhúng $\mathrm{Sym}^n K \to \mathrm{Sym}^{n+1}K, \sigma_1...\sigma_n \mapsto e_q \sigma_1...\sigma_q$ (nếu $\mathrm{dim}\sigma_i = q$) và gọi giới hạn của dãy $$K(e_0) = \mathrm{Sym}^0 K \subset \mathrm{Sym}^1 K \subset ... \subset \mathrm{Sym}^nK \subset ...$$ là tích đối xứng vô hạn của tập đơn hình $K$, kí hiệu $\mathrm{Sym}^{\infty}K$.

Sau đây, ta sẽ đi chứng minh $H_{\bullet}(\left|K \right|; G) \cong H_{\bullet}(\mathbb{Z}K;G)$ với mọi tập đơn hình $K$ và nhóm abel $G$. Nói riêng, $H_{\bullet}(\mathbb{Z}KG[-n]) \cong H_{\bullet}(K(G,n);\mathbb{Z})$.

 

Bổ đề 40. Nếu $f: (X, x_0) \to (Y,y_0)$ là một tương đương đồng luân thì $\mathrm{Sym}^nf$ cũng là một tương đương đồng luân với $n=0,1,...,\infty$.

 

Định lý 41. Với mọi tập đơn hình $K$ tồn tại một đồng luân yếu tự nhiên $$\left|\mathrm{Sym}^n K \right | \to \mathrm{Sym}^n \left|K \right|, \ \text{với} \ n = 0,1,...\infty.$$

 

Hệ quả 42. Cho $X$ là một CW-phức. Tồn tại một đồng luân yếu tự nhiên $\left|\mathrm{Sym}^{\infty}\mathrm{Sing}(X) \right| \to \mathrm{Sym}^{\infty}X$.

 

Chứng minh. Theo định lý 32 thì $j: \left|\mathrm{Sing}(X) \right| \to X$ là một đồng luân yếu nên theo định lý Whitehead cũng là một tương đương đồng luân ($\left|\mathrm{Sing}(X) \right|$ là một CW-phức). Theo bổ đề thì $\mathrm{Sym}^n j: \mathrm{Sym}^{\infty} \left| \mathrm{Sing}(X) \right| \to \mathrm{Sym}^{\infty}X$ là một tương đương đồng luân. Kết hợp với đồng luân yếu $\left| \mathrm{Sym}^{\infty} \mathrm{Sing}(X) \right| \to \mathrm{Sym}^{\infty} \left| \mathrm{Sing}(X) \right| $ ta có điều phải chứng minh.

 

Định lý 43. (Dold-Thom) Cho $K$ là một tập đơn hình liên thông khi đó $\mathrm{Sym}^n K$ cũng liên thông với $n= 0,1,...,\infty$. Hơn nữa, tồn tại một đẳng cấu tự nhiên $H_q(\mathbb{Z}K) \cong \pi_q(\mathrm{Sym}^{\infty}K)$ với mọi $q \geq 1$.

 

Bình luận. Chúng ta sẽ bình luận một chút về định lý Dold-Thom, nếu $K$ là một tập đơn hình, ta thấy rằng $\mathbb{Z}K$ sẽ là một vật đơn hình tự do trong phạm trù các nhóm abel, trong đó $(\mathbb{Z}K)_n = \mathbb{Z}K_n$. Nhưng ngoài ra $\mathrm{Sym}^{\infty}K$ cũng đóng một vai trò tương tự, nó là một vật đơn hình tự do trong phạm trù các monoid giao hoán. Như vậy theo tính phổ dụng của một vật tự do, ta sẽ có một cấu xạ tự nhiên $\mathrm{Sym}^{\infty}K \to \mathbb{Z}K$, định lý Dold-Thom nói rằng cấu xạ này cảm sinh đẳng cấu $\pi_{\bullet}(\mathrm{Sym}^{\infty}K) \overset{\cong}{\rightarrow} \pi_{\bullet}(\mathbb{Z}K) = H_{\bullet}(\mathbb{Z}K)$.

 

Hệ quả 44. Cho $X$ là một CW-phức liên thông, khi đó tồn tại một đẳng cấu tự nhiên $H_q(X) \cong \pi_q(\mathrm{Sym}^{\infty}X)$ với mọi $q \geq 1$. Nói riêng, $\mathrm{Sym}^{\infty}M(G,n) = K(G,n)$ với mọi nhóm abel $G$ và $n \geq 1$.

 

Chứng minh. Nếu $X$ liên thông thì $\mathrm{Sing}(X)$ cũng liên thông nên theo định lý 43
$$H_q(X) = H_q(\mathbb{Z}\mathrm{Sing}(X)) \cong \pi_q(\mathrm{Sym}^{\infty}\mathrm{Sing}(X)).$$ Dễ thấy $\mathrm{Sym}^{\infty}\mathrm{Sing}(X)$ là một vật đơn hình trong phạm trù các monoid abel. Theo định lý 31 ta có một đẳng cấu $\pi_q(\mathrm{Sym}^{\infty}\mathrm{Sing}(X)) \cong \pi_q(\left|\mathrm{Sym}^{\infty}\mathrm{Sing}(X) \right|)$ và lại theo hệ quả 42 thì $\pi_q(\left|\mathrm{Sym}^{\infty}\mathrm{Sing}(X) \right|) \cong \pi_q(\mathrm{Sym}^{\infty}X)$. Khẳng định thứ hai là hệ quả hiển nhiên của khẳng định thứ nhất.

 

Hệ quả 45 Cho $K$ là một tập đơn hình, khi đó tồn tại một đẳng cấu tự nhiên $H_q(\mathbb{Z}K) \cong H_q(\left|K\right|;\mathbb{Z})$ với mọi $q \geq 1$. Kết quả tương tự cũng đúng với đồng điều hệ số bất kỳ.

 

Định lý 46. Một $H$-không gian liên thông đường, giao hoán, kết hợp với một phần tử đơn vị chặt (strict) có kiểu đồng luân yếu của tích các không gian Eilenberg-MacLane.

Tương ứng Dold-Kan

 

Sau đây ta sẽ phát biểu một phần của tương ứng Dold-Kan. 

 

Định lý 16(Dold-Kan). Hàm tử phức chuẩn hóa $N: s\mathbf{Ab} \to \mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ là một hàm tử đầy đủ, trung thành, nói cách khác,

$$N: \mathrm{Hom}_{s\mathbf{Ab}}(A,B) \cong \mathrm{Hom}_{\mathbf{Ch}_{\geq0}}(NA,NB) \ \forall \ A,B \in s\mathbf{Ab}. $$

Để chứng minh nó ta cần bổ đề sau. 

 

Bổ đề 17. Với mọi $a \in A_n$ ta có một phân tích (duy nhất, tuy nhiên ta chỉ chứng minh sự tồn tại) dạng 

$$x = \sum_{\beta} A(\beta)(x_{\beta}),$$

trong đó $x_{\beta} \in (NA)_p$ và $\beta: [n] \twoheadrightarrow [p]$. 

 

Chứng minh. Nhắc lại rằng $a = b+ \sum_{i=0}^n s_i(a_i)$ với $b \in (NA)_n, a_i \in A_{n-1}$. Theo giả thiết quy nạp $a_i = \sum A(\beta')(x_{\beta'})$ với $\beta:[n-1] \twoheadrightarrow [p]$ và nhắc lại từ phân tích đơn-toàn cấu mỗi toàn cấu $[n] \twoheadrightarrow [p]$ được phân tích thành $[n] \to [n-1] \to [p]$ với $[n-1] \to [p]$ là một đối suy biến. 

 

Chứng minh định lý Dold-Kan. Trước tiên ta chứng minh $N$ là đơn cấu, giả sử $f: A \to B$ là một cấu xạ giữa hai nhóm abel đơn hình với $N(f) = 0$. Với $a \in A_n$ ta viết $a = \sum A(\beta)(x_{\beta})$, do đó 

\begin{align*} f(x) & = f\left( \sum A(\beta)(x_{\beta}) \right) \\ & = \sum f\left(A(\beta)(x_{\beta})\right) \\ & = \sum B(\beta)(f(x_{\beta})) \\ & = \sum B(\beta)(N(f)(x_{\beta})) = 0. \end{align*} Tiếp theo ta chứng minh $N$ là toàn cấu, lấy $g: NA \to NB$, ta đặt $f: A \to B$ trong đó

$$f(x) = \sum B(\beta)(x_{\beta}),$$

với $x = \sum A(\beta)(x_{\beta})$. Dễ kiểm tra $Nf = g$. 

 

Giờ ta sẽ tìm nghịch đảo của $N$ là một hàm tử $K: \mathbf{Ch}_{\geq 0}(\mathbf{Ab}) \to s\mathbf{Ab}$.

 

Định nghĩa 18. Định nghĩa hàm tử $K$ bởi $KC = \mathrm{Hom}_{\mathbf{Ch}_{\geq 0}}(N\mathbb{Z}\Delta[\square],C)$. 

 

Mệnh đề 19. Ta có một đẳng cấu $A \cong (KNA)$ với mọi nhóm abel đơn hình $A$. 

 

Chứng minh. Điều này suy ta từ định nghĩa

$$A_n \cong \mathrm{Hom}(\mathbb{Z}\Delta[n],A) \cong \mathrm{Hom}(N\mathbb{Z}\Delta[n],NA) = (KNA)_n.$$

Trước khi đi tiếp ta cần một bổ đề kĩ thuật, ta sẽ không chứng minh. 

 

Bổ đề 20. Với mỗi $n$ thì $(N\mathbb{Z}\Delta[n])_m$ là nhóm abel tự do với cơ sở là các đơn ánh $[m] \hookrightarrow [n]$. Bên cạnh đó với mỗi cấu xạ dây chuyền $f: N\mathbb{Z}\Delta[n] \to C$ thì $f \in D_n(KC)$ khi và chỉ khi $f_r = 0 \ \forall r \geq n$. 

Về khẳng định thứ hai của bổ đề ta có thể hiểu nôm na nếu như $f = \sum_{i=0}^n s_i(f_i)$ với $f_i: N\mathbb{Z}\Delta[n-1] \to C$, tuy nhiên $N\mathbb{Z}\Delta[n-1])_r = 0$ do không có đơn cấu nào $[r] \hookrightarrow [n-1]$.

 

Mệnh đề 21. Với mỗi $n$ ta có một đẳng cấu $\phi_n: (NKC)_n \to C_n, f \mapsto f_n(\mathrm{id}_{[n]})$; họ đẳng cấu này cho ta một đẳng cấu giữa hai phức $NKC \cong C$. 

 

Phác thảo chứng minh. Trước hết ta cần xem $NKC$ "trông" như thế nào

$$(NKC)_n = \bigcap_{i=1}^n \mathrm{Ker}\left(d_i: \mathrm{Hom}(N\mathbb{Z}\Delta[n],C) \to \mathrm{Hom}(N\mathbb{Z}\Delta[n-1],C) \right).$$

Như vậy nếu $f \in (NKC)_n$ thì $d_i(f) = f \circ d^i = 0$ với mọi $i>0$. Bây giờ ta chứng minh tính đơn ánh, giả sử $f \in \mathrm{Ker}(\phi_n)$ thì hiển nhiên $f_r = 0 \ \forall r > n$ và $f_n(\mathrm{id}_{[n]})=0$ suy ra $f_n = 0$. Theo bổ đề trước thì $f \in D_n(KC)$, tuy nhiên $f \in N_n(KC)$ nên $f = 0$ theo bổ đề $N \cap D = 0$.

 

Về tính toàn ánh, với mỗi $x \in C_n$ ta xét $g$ thỏa mãn $g_r \equiv 0$ với mọi $r \neq n,n-1$; $g_n(\mathrm{id}_{[n]}) = x$ và 

$$g_{n-1}(d^i) =  \begin{cases} \partial(x) & i = 0, \\ 0 & i > 0 \end{cases}$$

Khi đó dễ kiểm tra $\phi_n(g) = x$. 

 

Định lý tương ứng Dold-Kan đầy đủ. Hai hàm tử $(N,K)$ là một cặp tương đương. Hơn thế nữa, tương đương này còn bảo toàn đồng luân theo nghĩa chặt, nói như vậy có nghĩa trong cả hai phạm trù $s\mathbf{Ab},\mathbf{Ch}_{\geq 0}(\mathbf{Ab})$ đều có các quan hệ đồng luân và chúng được bảo toàn hoàn toàn qua $N,K$ theo nghĩa: đồng luân trong phạm trù này khi và chỉ khi đồng luân trong phạm trù kia sau khi áp dụng hàm tử.

Lý thuyết motives xuất hiện để đưa ra lời giải cho việc hợp nhất hai loại lý thuyết đối đồng điều: đối đồng điều thuộc kiểu bất biến hình học-đại số và đối đồng điều thuộc kiểu bất biến siêu việt. Lớp thứ nhất có thể kể tới nhóm Chow và Quillen K-lý thuyết trong khi đó nhóm thứ hai có thể kể tới đối đồng điều Betti và đối đồng điều $l$-adic. Đối đồng điều thuộc loại thứ nhất thường abel và không thể tính toán, Deligne và Beillinson là những người đầu tiên tin rằng nếu đi theo các đối đồng kiểu bất biến hình học-đại số thì sẽ dễ hơn loại thứ hai. Có ba lý thuyết motives tương đương xây dựng bởi Hanamura, Levine và Voevodsky nhưng xây dựng của Voevodsky được cho là đẹp nhất. Những xây dựng đầu tiên của Grothendieck của các Chow motives được cải thiện và trình bày trong một cuốn sách của Levine, ở đây họ xây dựng các phạm trù effective Chow motives theo kiểu đồng điều $M^{eff}(\mathrm{Spec}(k))$ và theo kiểu đồng điều $M_{eff}(\mathrm{Spec}(k))$ chủ yếu dựa vào chu trình đại số và tương đương hữu tỷ nhưng tương đương hữu tỷ làm mất nhiều thông tin và xây dựng này gặp nhiều trục trặc kĩ thuật. Trong bài viết này mình sẽ trình bày xây dựng của Voevodsky vốn được xem là một cải thiện xây dựng cho $M^{eff}$ và phiên bản cải thiện của chính Voevodsky dựa trên lý thuyết $\mathbb{A}^1$-đồng luân, điều đáng kể của phiên bản đơn giản hóa của xây dựng của Voevodsky là nó làm việc được trên mọi lược đồ nền.

 

Mình sẽ trình bày phiên bản đơn giản của phiên bản đầu của Voevodsky trước. Sau đó mình sẽ định nghĩa đối đồng điều motivic dựa trên đồng điều Suslin và trình bày một số tính chất của nó.

 

Ý tưởng của lý thuyết $\mathbb{A}^1$-đồng luân là thay thế đoạn đơn vị $[0,1]$ trong topo bởi đường thẳng affine $\mathbb{A}^1 = \mathrm{Spec}(\mathbb{Z}[t])$. Trong lý thuyết đối đồng điều kì dị và một số loại đối đồng điều cho đa tạp đại số ta biết có tính chất $H^{*}(X) \cong H^*(X \times \mathbb{A}^1)$, đây gọi tính $\mathbb{A}^1$--đồng luân và nó luôn đóng vai trò chủ chốt trong mọi xây dựn, một lý thuyết đối đồng điều thường được biểu diễn bởi hàm tử hom trong một phạm trù tam giác hợp lý (hãy nghĩ điều này trong phiên bản topo với định lý biểu diễn Brown). Lấy ví dụ nếu $T$ là một không gian topo, khi đó đối đồng điều bó với hệ số trong một nhóm abel $A$ có thể biểu diễn theo hai cách

$$H^n(T,A) = \mathrm{Ext}^n_{\mathbf{Sh}(T,\mathbf{Ab}) }(\mathbb{Z}_T,A_T) = \mathrm{Hom}_{\mathbf{D}(\mathbf{Sh}(T,\mathbf{Ab}))}(\mathbb{Z}_T,A_T[n]),$$

trong đó $G_T$ là bó hằng với giá trị tại một nhóm abel $G$ và $\mathbf{D}$ là phạm trù dẫn suất.

 

$\mathbb{A}^1$-địa phương hóa. Cho $R$ là một vành giao hoán có đơn vị, với mỗi tập $E$ ta kí hiệu $R \otimes E$ bởi $R$-module tự do với một cơ sở là $E$. Cho $S$ là một lược đồ bất kì, ta kí hiệu $Sm/S$ bởi phạm trù các lược đồ trơn trên $S$ và trang bị cho $Sm/S$ topo étale. Kí hiệu $\mathbf{Sh}_{ét}(Sm/S;R)$ bởi phạm trù các bó étale trên small étale site $Sm/S$ với giá trị trong $\mathrm{Mod}_R$-phạm trù các $R$-module. Với mỗi $X \in \mathrm{obj}(Sm/S)$ ta có một hàm tử

$$\begin{align*} R_{ét}: Sm/S & \to \mathbf{Sh}_{ét}(Sm/S;R) \\ X & \mapsto \left \{ U \mapsto R \otimes \mathrm{Hom}_S(U,X) \right \} \end{align*}$$

Phạm trù $\mathbf{Sh}(Sm/S;R)$ được trang bị một cấu trúc tensor: nếu $\mathcal{F},\mathcal{G}$ là hai bó etale thì $\mathcal{F} \otimes_R \mathcal{G}$ là bó hóa của tiền bó $U \mapsto \mathcal{F}(U) \otimes_R \mathcal{G}(U)$. Giờ để làm đối đồng điều ta xét phạm trù dẫn xuất $\mathbf{D}(\mathbf{Sh}(Sm/S;R))$ và sau đó để "áp đặt" tính $\mathbb{A}^1$-đồng luân ta ký hiệu $\mathcal{T}_{\mathbb{A}^1}$ bởi phạm trù tam giác con nhỏ nhất đóng bởi tổng trực tiếp và chứa tất cả các phức dạng

$$[... \to R_{ét}(\mathbb{A}^1 \times U) \to R_{ét}(U) \to 0 \to ...],$$

trong đó $U$ là một $S$-lược đồ trơn. Lưu ý với mỗi $U$ ta có vô hạn phức như trên tùy vào cách đặt bậc, lý do là ta "nên" có $H^*(X) \cong H^*(X \times [0,1])$ tại mọi bậc.

 

Định nghĩa. Ta định nghĩa các $S$-motive effective $\mathbf{DA}^{eff,ét}(S;R)$ là phạm trù $\mathbf{D}(\mathbf{Sh}_{ét}(Sm/S;R))/\mathcal{T}_{\mathbb{A}^1}$, ở đây ta lấy thương Verdie, về mặt các vật thì nó có cùng các vật với $\mathbf{D}(\mathbf{Sh}_{ét}(Sm/S;R))$ nhưng khi chuyển vào phạm trù thương thì mọi vật của $\mathcal{T}_{\mathbb{A}^1}$ đẳng cấu với $0$. Với mỗi $S$-lược đồ trơn $X$, ký hiệu $M^{eff}(X)$ bởi ảnh của $X$ qua hợp thành

$$Sm/S \overset{R_{ét}}{\rightarrow} \mathbf{Sh}(Sm/S;R) \to \mathbf{D}( \mathbf{Sh}(Sm/S;R  ) ) \to \mathbf{DA}^{eff,ét}(S;R),$$

và ta gọi $M^{eff}(X)$ là motive đối đồng điều effective của $X$.

 

Lấy động lực từ đối đồng điều $l$-adic (đoạn này mình cũng không rõ vì từ trước tới giờ chỉ mới đụng tới đối đồng điều étale) ta sẽ địa phương hóa phạm trù $\mathbf{DA}^{eff,ét}$ theo motive Lefschetz $L = R_{ét}(\mathbb{P}^1_S,\infty_S)$. Ta định nghĩa ổn định hóa naive (naive stabilization) $\mathbf{DA}^{naive,ét}$ bởi

$$\mathbf{DA}^{naive,ét}(S;R) = \mathbf{DA}^{eff,ét}(S;R)[L^{-1}],$$

trong đó một vật là một cặp $(M,m)$ với $M \in \mathrm{obj}(\mathbf{DA}^{eff,ét})$ và $m \in \mathbb{Z}$. Cấu xạ được cho bởi

$$\mathrm{Hom}_{\mathbf{DA}^{naive,ét}(S;R)}((M,m),(N,n)) = \underset{\underset{r \geq -\mathrm{min}(m,n)}{\longrightarrow}}{\lim} \mathrm{Hom}_{\mathbf{DA}^{eff,ét}(S;R)}(M \otimes L^{r+m}, N \otimes L^{r+n}).$$

(ta sẽ gặp lại xây dựng này trong phiên bản đầu tiên của Voevodsky). Phạm trù $\mathbf{DA}^{naive,ét}$ được tin là đủ tốt để trở thành định nghĩa của phạm trù $S$-motive, tuy nhiên nó gặp nhiều vấn đề kĩ thuật; ví dụ đơn giản nhất là nó không phải phạm trù tam giác.

 

$L$-phổ và đối đồng điều étale motivic. Ta vẫn giữ nguyên ký hiệu $L = R_{ét}(\mathbb{P}^1_S;\infty_S)$, một $L$-phổ của các bó é tale trên $Sm/S$ là một dãy các bó étale $\mathcal{E}=(\mathcal{E}_n)$ ($n \in \mathbb{N})$ và một dãy các đẳng cấu mà ta gọi là các assembly map, $\gamma_n: L \otimes \mathcal{E}_n \to \mathcal{E}_{n+1}$. Ta định nghĩa cấu xạ giữa hai $L$-phổ theo cách hiển nhiên tương thích với các assembly map và ký hiệu $\mathrm{Spt}_L(\mathbf{Sh}_{ét}(Sm/S;R))$ bởi phạm trù các $L$-phổ.

 

Hàm tử

$$\begin{align*} \mathrm{Ev}_p: \mathrm{Spt}_L(\mathbf{Sh}_{ét}(Sm/S;R)) & \to \mathbf{Sh}_{ét}(Sm/S;R) \\ ((\mathcal{E}_n),(\gamma_n)) & \mapsto \mathcal{E}_n \end{align*}$$ gửi mỗi phổ $((\mathcal{E}_n),(\gamma_n))$ tới bậc thứ $p$ của nó có một hàm tử liên hợp được ký hiệu bởi

$$\mathrm{Sus}^p_L: \mathrm{Sh}_{ét}(Sm/S;R) \to \mathrm{Spt}_L(\mathbf{Sh}_{ét}(Sm/S;R)).$$

Ta ký hiệu $\mathrm{Sus}^0_L$ bởi $\Sigma^{\infty}_L$. Như thường lệ, ta xét $\mathbf{D}(\mathrm{Spt}_L(\mathbf{Sh}_{ét}(Sm/S;R)))$ là phạm trù dẫn xuất của phạm trù các $L$-phổ, ký hiệu $\mathcal{T}_{\mathbb{A}^1-st}$ bởi phạm trù tam giác con nhỏ nhất của $\mathbf{D}(\mathrm{Spt}_L(\mathbf{Sh}_{ét}(Sm/S;R)))$ mà đóng với phép lấy tổng trực tiếp tùy ý đồng thời chứa tất cả các phức dạng

$$[... \to 0 \to \mathrm{Sus}^p_L R_{ét}(\mathbb{A}^1 \times U) \to \mathrm{Sus}^p_L R_{ét}(U) \to 0 \to ... ],$$

$$[... \to 0 \to \mathrm{Sus}^{p+1}_L R_{ét}(L \otimes U) \to \mathrm{Sus}^p_L R_{ét}(U) \to 0 \to ...].$$

Định nghĩa. Ta định nghĩa phạm trù các bó motivic trên $S$ (hoặc đơn giản, các $S$-motive), ký hiệu $\mathbf{DA}^{ét}(S;R)$, bởi công thức

$$\mathbf{DA}^{ét}(S;R) = \mathbf{D}(\mathrm{Spt}_L(\mathbf{Sh}_{ét}(Sm/S;R)))/\mathbf{T}_{\mathbb{A}^1-st}.$$

Với mỗi $S$-lược đồ trơn $S$, thì $\Sigma_L^{\infty}R_{ét}(X)$ xem như một vật của $\mathbf{DA}^{ét}(S;R)$ được gọi là motive đồng điều của $X$ và sẽ được ký hiệu bởi $M(X)$.

 

Định nghĩa. (đối đồng điều étale motivic) Ta định nghia các Tate motive $R_S(p)$ bởi công thức $R_S(p) = \mathrm{Sus}^0_L(L^{\otimes p})[-2p]$ và định nghĩa

$$H^p_{\mathcal{L}}(S;R(p)) = \mathrm{Hom}_{\mathbf{DA}^{ét}(S;R)}(R(0), R(q)[p]),$$

với mọi $p,q \in \mathbb{Z}$. Các nhóm này được gọi là đối đồng điều étale motivic của lược đồ $S$.

 

Định nghĩa. (nhóm Chow étale) Cho $k$ là một trường, $X$ là một đa tạp trơn trên $k$. Ta định nghĩa nhóm Chow étale của $X$ bởi

$$\mathrm{CH}^{2n}_{ét}(X) = H^{2n}_{\mathcal{L}}(X;\mathbb{Z}(n)) = \mathrm{Hom}_{\mathbf{DA}^{ét}(k;\mathbb{Z})}(M(X),\mathbb{Z}(n)[2]).$$

Rosenschon và Srinivas xây dựng một cấu xạ chu trình khi $k = \mathbb{C}$, $\mathrm{CH}_{ét}^{2n}(X) \to H^{2n}(X(\mathbb{C});\mathbb{Z})$ và chứng minh rằng nếu giả thuyết Hodge đúng cho nhóm Chow hữu tỷ $\mathrm{Ch}^*(X) \otimes \mathbb{Q}$ thì nó đúng cho nhóm Chow étale với hệ số trên $\mathbb{Z}$.

Trong post này mình sẽ định nghĩa một số phạm trù đồng luân ổn định được dùng trong hình học đại số, sau đó formulate $K$-lý thuyết đại số theo ngôn ngữ motivic.Trong bài viết này, $k$ là một trường và $Sm/k$ là phạm trù các $k$-lược đồ trơn, of finite type và tách được.

Topo Nisnevich. Cho $X \in \mathrm{obj}(Sm/k)$, một phủ Nisnevich $\mathcal{U} \to X$ là một cấu xạ étale sao cho với mọi mở rộng $F$ hữu hạn sinh như một $k$-đại số, tách được thì ánh xạ trên các $F$-điểm $\mathcal{U}(F) \to X(F)$ là một toàn cấu. Với phủ Nisnevich ta có thể định nghĩa một small Nisnevich site trên $Sm/k$ cũng như $X_{Nis}$.

Trong bài viết này về sau, khi nói một không gian, ta ám chỉ một phần tử trong
$$\mathrm{Spc}(k) = \mathbf{Sh}_{Nis}(Sm/k,\mathbf{Sets}^{\Delta^{op}}).$$
Nói cách khác, một không gian là một bó trên $Sm/k$ (cùng topo Nisnevich) lấy giá trị trong phạm trù các tập đơn hình.

Định nghĩa. Một điểm trong một không gian $X$ là một cấu xạ $\mathrm{Spec}(k) \to X$ trong đó $\mathrm{Spec}(k)$ xem như một bó biểu diễn được với cấu trúc đơn hình là hằng. Nếu $X$ là một không gian thì ta ký hiệu $X_{+}$ bởi không gian định điểm $X \coprod \mathrm{Spec}(k)$ và $\mathrm{Spc}_{\bullet}(k)$ là phạm trù các không gian định điểm. Ta viết $\mathbb{P}^1$ để hiểu không gian định điểm $(\mathbb{P}^1_k,\infty_k)$.

Phạm trù $\mathrm{Spc}_{\bullet}$ là một phạm trù tensor với cấu trúc monoid cho bởi tích smash $U \mapsto X(U) \wedge Y(U)$ và vật đơn vị chính là $\mathrm{Spec}(k)_+$.

$\mathbb{P}^1$-phổ và nhóm đồng luân ổn định. Một $\mathbb{P}^1$-phổ $E$ là một dãy các không gian định điểm $(E_n)_{n\geq 0}$ cùng với các cấu xạ cấu trúc $\mathbb{P}^1 \wedge E_n \to E_{n+1}$. Một cấu xạ giữa hai phổ là các cấu xạ theo từng bậc và tương thích với cấu xạ cấu trúc. Phạm trù $\mathrm{Spt}_{\mathbb{P^1}}(k)$ có vật là các $\mathbb{P}^1$-phổ và cấu xạ định nghĩa theo cách tự nhiên.

Ví dụ. 1) $\mathbb{P}^1$-phổ treo của một không gian định điểm $X$, ký hiệu $\Sigma_{\mathbb{P}^1}^{\infty}X$ là phổ $(\mathbb{P}^1)^{\wedge n} \wedge X$ và các cấu xạ cấu trúc là cấu xạ đồng nhất.
2) Nếu $E$ là một $\mathbb{P}^1$-phổ và $X$ là một không gian định điểm thì ta có phổ mới $(E \wedge X)_n = E_n \wedge X$.

Định nghĩa (nhóm đồng luân ổn định). Cho $(X,x)$ là một không gian định điểm và $n \geq 1$, ta xét tiền bó $U \mapsto \pi_n(X(U), x_{\mid U}),$ trong đó $x_{\mid U}$ là ảnh của $x$ trong $X(U)$. Bó hóa của tiền bó này được ký hiệu bởi $\pi_n(X,x)$. Khi $n \geq 2$ thì đây là một bó các Nisnevich các nhóm abel. Bây giờ cho $(E_n)_{n \geq 0}$ là một $s$-phổ và $m > n$ là các số nguyên, ta xét dãy
$$\pi_{n+m}(E_m) \to \pi_{n+m+1}(S^1_s \wedge E_m) \to \pi_{n+m+1}(E_{m+1}) \to \cdots,$$
và định nghĩa bó các nhóm đồng luân ổn định của $E$ bởi $\pi_n^s(E) = \underset{m > n}{\mathrm{colim}} \pi_{n+m}(E_m).$ Hiển nhiên một cấu xạ giữa hai $s$-phổ cho ta cấu xạ trên các nhóm đồng luân ổn định và do đó ta có thể định nghĩa khái niệm đồng luân yếu giống như trong setting thông thường.

Định nghĩa. Phạm trù $\mathrm{SH}_{\mathbb{P}^1}(k)$ được định nghia là phạm trù $\mathrm{Spt}(k)$ sau khi nghịch đảo tất cả các đồng luân yếu.

Phạm trù đồng luân $\mathbb{P}^1$-ổn định motivic. Một $\mathbb{P}^1$-phổ được gọi là $\mathbb{A}^1$-địa phương nếu với mọi $U \in \mathrm{obj}(Sm/k)$, $n \in \mathbb{N}$ thì cấu xạ cảm sinh bởi phép chiếu $U \times \mathbb{A}^1 \to U$ là một đẳng cấu
$$\mathrm{Hom}_{\mathrm{SH}_{\mathbb{P}^1}(k)}(\Sigma_{\mathbb{P}^1}^{\infty}(U \times \mathbb{A}^1)_{+},\Sigma^n_{\mathbb{P}^1}F) \overset{\cong}{\leftarrow} \mathrm{Hom}_{\mathrm{SH}_{\mathbb{P}^1}(k)}(\Sigma_{\mathbb{P}^1}^{\infty}U_{+},\Sigma^n_{\mathbb{P}^1}F).$$
Ta nói một cấu xạ của hai $\mathbb{P}^1$-phổ $E \to F$ là $\mathbb{A}^1$-đồng luân yếu nếu với mọi $\mathbb{P}^1$-phổ $\mathbb{A}^1$-địa phương $E'$ tồn tại đẳng cấu chính tắc
$$\mathrm{Hom}_{\mathrm{SH}_{\mathbb{P}^1}(k)}(E',F) \to \mathrm{Hom}_{\mathrm{SH}_{\mathbb{P}^1}(k)}(E,E').$$
Định nghĩa. Phạm trù đồng luân $\mathbb{P}^1$-ổn định motivic $\mathrm{SH}_{\mathbb{P}^1}^{\mathbb{A}^1}(k)$ được định nghĩa là phạm trù $\mathrm{Spt}(k)$ sau khi nghịch đảo tất cả các $\mathbb{A}^1$-đồng luân yếu.

Như vậy ta có bổ đề hiển nhiên sau.

Bổ đề. Trong $\mathrm{SH}_{\mathbb{P}^1}^{\mathbb{A}^1}(k)$ thì $X \times \mathbb{A}^1 \to X$ cảm sinh $\mathbb{A}^1$-đồng luân yếu của các $\mathbb{P}^1$-phổ. Nói riêng, $\Sigma^{\infty}_{\mathbb{P}^1}(\mathbb{A}^1,0)$ là co rút được (contractible). Hàm tử treo $\mathbb{P}^1 \wedge \square$ là một tự tương đương của phạm trù $\mathrm{SH}_{\mathbb{P}^1}^{\mathbb{A}^1}(k)$.

Bây giờ ta đã đủ công cụ để formulate $K$-lý thuyết đại số, ta nhắc lại rằng nhóm $K$-lý thuyết topo $K^n$ được biểu diễn bởi $\mathbb{Z} \times BU(n)$ trong đó $BU(n)$ là không gian phân loại của nhóm unita $U(n)$ và $BU(n)$ còn có biểu diễn khác là Grassmanian $Gr(n,\mathbb{C}^{\infty})$. Một cách hiển nhiên ta phải đụng tới Grassmanian ở đây. Với $m,n$ không âm ta xét Grassmanian của các không gian vector $n$ chiều trong không gian $(n+m)$ chiều bởi $Gr(n,\mathbb{A}^{n+m})$ và cho $n$ tới vô cùng ta thu được một directed system, gọi giới hạn của hệ này là $BGL(n)$. Các không gian phân loại này lại lập này một hệ
$$...\hookrightarrow BGL_n \hookrightarrow BGL_{n+1} \hookrightarrow ....,$$
và ta ký hiệu $BGL$ bởi đối giới hạn của hệ này. Trong lý thuyết đơn hình ta có một hàm tử gọi là "thay thế fibrant" $Ex^{\infty}$ có tính chất là nếu $X$ là một tập đơn hình định điểm thì $X \subset Ex^{\infty}X$ là một đồng luân yếu và $Ex^{\infty}X$ là fibrant, tức là có tính chất nâng với mọi horn. Ký hiệu $KGL = Ex^{\infty}(\mathbb{Z} \times BGL)$. Voevodsky trong IMC talk năm 98 viết rằng lý do ông lấy thay thế fibrant vì ông muốn định nghĩa một cấu xạ cấu trúc $\mathbb{P}^1 \wedge (\mathbb{Z} \times BGL) \to \mathbb{Z} \times BGL$ thì cách duy nhất mà ông biết là định nghĩa nó trong phạm trù đồng luân và nói rằng mọi cấu xạ trong phạm trù đồng luân với giá trị là vật fibrant thì có thể nâng lên phạm trù các không gian. Như vậy ta có một cấu xạ cấu trúc $\mathbb{P}^1 \wedge KGL \to KGL$.

Định nghĩa. Phổ của $K$-lý thuyết đại số được định nghĩa bởi $\mathbf{KGL}=(KGL,KGL,..,KGL,...)$ cùng với cấu xạ cấu trúc $\mathbb{P}^1 \wedge KGL \to KGL.$ Ta có một đẳng cấu $\mathbb{P}^1 \wedge \mathbf{KGL} = \mathbf{KGL}$ và gọi đây là định lý tuần hoàn Bott cho $K$-lý thuyết đại số.

Trong bài này mình sẽ trình bày phạm trù các motive hình học effective, để làm vậy ta nhắc lại một số khái niệm trong lý thuyết giao (intersection theory) như chu trình đại số, tương ứng hữu hạn (finite correspondence),... Ta cố định $k$ là một trường, $Sm/k$ là phạm trù các $k$-lược đồ trơn, $Sch/k$ là phạm trù các $k$-lược đồ.

 

Chu trình đại số. Cho $X \in \mathrm{obj}(Sch/k)$, ký hiệu $z_r(X) = \bigoplus \mathbb{Z}.Z$ trong đó $Z$ là một lược đồ con đóng nguyên trên $k$, chiều $r$. Ký hiệu $z_*(X) = \bigoplus_{r \geq 0}z_r(X)$. Một phần tử của $z_*(X)$ được gọi là một chu trình đại số.

 

Chu trình cảm sinh và giá. Cho $W \subset X$ là một lược đồ con đóng sao cho tất cả các thành phần bất khả quy $W_1,...,W_r$ có chiều $n$. Chu trình đại số cảm sinh bởi $W$ được định nghĩa bởi

$$\left |W \right| = \sum_{i=1}^r \mathrm{length}_{\mathcal{O}_{X,W_i}}(\mathcal{O}_{W,W_i})W_i,$$

trong đó $\mathrm{length}$ là độ dài của một module, ở đây khi viết $\mathcal{O}_{X,W_i}$ ta đồng nhất nó với $\mathcal{O}_{X,\eta}$ trong đó $\eta$ là điểm generic của $W_i$. Cho $D$ là một ước Cartier trên $X$ và $Z \subset X$ là một lược đồ con đóng nguyên, ta định nghĩa tích giao $D \cdot Z$ bởi

$$D \cdot Z = \left | D \times_X Z \right|.$$

Ký hiệu $z_n(X)_D \subset z_n(X)$ là nhóm abel tự do sinh bởi các lược đồ con đóng nguyên $Z$ sao cho $Z \nsubseteq D$.

 

Định nghĩa. Cho $X \in \mathrm{obj}(Sch/k)$, hai chu trình $Z, Z' \in z_n(X)$ được gọi là tương đương hữu tỷ nếu tồn tại một chu trình $\mathcal{Z} \in z_{n+1}(X \times \mathbb{A}^1_k)_{X \times 0+ X \times 1}$ sao cho

$$Z - Z' = (X \times 0 - X \times 1) \cdot \mathcal{Z}.$$

Nhóm Chow thứ $n$ được định nghĩa bởi $\mathrm{CH}_n(X) = z_n(X)/\text{tương đương hữu tỷ}.$

 

Tương ứng. Một phần tử của $\mathrm{CH}_*(X \times Y)$ được gọi là một tương ứng từ $X$ tới $Y$. Nếu $X, Y$ và $Z$ là các được đồ trơn, xạ ảnh thì ta có thể định nghĩa phép hợp thành

$$\beta \circ \alpha = p_{XZ*}(p_{XY}^*(\alpha) \cdot p_{YZ}^*(\beta)),$$

trong đó $p_{XY}: X \times Y \times Z \to X \times Y$ là phép chiếu.

 

Tương ứng hữu hạn. Cho $X, Y \in \mathrm{obj}(Sch/k)$. Nhóm $c(X,Y)$ là nhóm con của $z(X \times_k Y)$ sinh bởi các lược đồ con đóng nguyên $W \subset X \times_k Y$ sao cho:

 

i) $p_1:W \to X$ là hữu hạn;

ii) $p_1(W)$ là một thành phần bất khả quy của $W$.  

 

Các phần tử của $c(X,Y)$ được gọi là các tương ứng hữu hạn từ $X$ tới $Y$.

 

Mình không thực sự hiểu ý nghĩa của finite correspondence, ngay cả correspondence cũng vậy. Theo như wiki thì correspondence là một quan hệ định nghĩa bởi các phương trình đại số. Nhưng để hiểu tại sao nó lại được dùng để định nghĩa cấu xạ của phạm trù motive hình học thì mình vẫn chưa hiểu. Tính finite ở đây trong finite correspondence mang tính kỹ thuật nhiều hơn, được Voevdosky đưa ra nhằm mở rộng lớp các đa tạp có thể lấy hợp thành được. Tương tự như correspondence ta định nghĩa hợp thành bởi

$$W' \circ W = p_{XZ*}^S(p^*_{XY}(W) \cdot p^*_{YZ}(W')),$$

trong đó $W \in c(X,Y), W' \in c(Y,Z)$ và $X,Y,Z \in \mathrm{obj}(Sm/k)$, $S = \mathrm{supp}(W) \times Z \cap  X \times \mathrm{supp}(W')$ và $p_{XZ}^S: S \to X \times Z$ là phép chiếu cảm sinh bởi $p_{XZ}$.

 

Câu hỏi. Có cách nào nhìn trực giác được công thức trên thỏa mãn luật kết hợp của phép hợp thành cấu xạ không?

 

Ví dụ. Ở đây ta sẽ tính toán thử một ví dụ về correspondence để "lấy cảm giác", cho $x$ là một điểm đóng trong $X$, xét lược đồ nền là $S = \mathrm{Spec}(k)$. Ta xem $x$ như correspondence $S \times x \in \mathrm{Cor}(S,X)$ và cấu xạ cấu trúc $X \to S$ như correspondence $X \times S \in \mathrm{Cor}(S,X)$. Tích giao của chúng theo định nghĩa là $[S \times x] \cdot [X \times S] = [S \times x \times S]$. Ta khẳng định rằng hợp thành của hai correspodence này $S \to X \to S$ là một correspondence $\mathrm{Cor}(S,S)$ ứng với đồng cấu nhân với $[k(x):k]$. Thực vậy ta cần tính đẩy xuôi của $p: S \times x times S \to S \times S$. Sử dụng đẳng cấu $S \times x \times S \cong S \times x, S \times S \cong S$ ta suy ra $p$ dẳng cấu với $S \times x \to S$, cấu xạ này hiển nhiên có bậc $[k(x):k]$ vì nó chỉ là base change từ $S = \mathrm{Spec}(k)$ sang $\mathrm{Spec}(k \otimes k(x))$.

 

Ta định nghĩa phạm trù $\mathrm{Cor}(k)$ có vật là các lược đồ trơn và cấu xạ cho bởi $\mathrm{Hom}_{\mathrm{cor}}(X,Y) = c(X,Y)$ với mọi $X,Y \in \mathrm{obj}(Sm/k)$. Tích thớ trên $k$ cho ta một cấu trúc tensor trên $\mathrm{Cor}(k)$. Ngoài ra ta có hàm tử $Sm/k \to \mathrm{Cor}(k)$ gửi mỗi vật vào chính nó và một cấu xạ $f : X\to Y$ tới đồ thị $\Gamma_f$ của nó, ta viết ảnh của một vật $X$ qua hàm tử này bởi $[X]$ và ảnh một cấu xạ $f$ bởi $f_*$. Xét phạm trù đồng luân các phức bị chặn $K^b(\mathrm{Cor}(k))$.

 

Định nghĩa. Phạm trù $\widehat{\mathbf{DM}}^{eff}_{gm}(k)$ được định nghĩa là địa phương hóa của $K^b(\mathrm{Cor}(k))$ bằng cách nghịch đảo các cấu xạ sau:

 

i) Với mọi $X \in \mathrm{obj}(Sm/k)$, $p_*: [X \times \mathbb{A}^1_k] \to [X]$;

ii) Với mọi $X \in \mathrm{obj}(Sm/k)$ và một cặp tập mở $U, V \subset X$ sao cho $X = U \cup V$ thì ta nghịch đảo $\mathrm{cone}([U \cap V] \to [U] \oplus [V]) \to [X]$.

Điều kiện thứ nhất để sinh ra tính $\mathbb{A}^1$-đồng luân, điều kiện thứ hai cho ta dãy Mayer-Vietoris. Phạm trù các motive hình học effective $\widehat{\mathbf{DM}}^{eff}_{gm}(k)$ được định nghĩa là giả abel envelope của $\widehat{\mathbf{DM}}^{eff}_{gm}(k)$.

 

Tương tự như trên, ta có một hàm tử $Sm/k \to \mathbf{DM}^{eff}_{gm}(k)$ gửi mỗi lược đồ trơn $X$ tới chính nó, mà ta ký hiệu bởi $M(X)$; và gửi một cấu xạ tới đồ thị của nó. Như trong bài viết trước, ta cần nghịch đảo motive Lefschetz, cụ thể, ta xét Tate motive

$$\mathbb{Z}(1) = \mathrm{Cone}(p_*:[X] \to [\mathrm{Spec}(k)])[-1][2],$$

và đặt $\mathbb{Z}(n) = \mathbb{Z}(1)^{\otimes n}.$ Phạm trù các motive hình học $\mathbf{DM}_{gm}(k)$ được định nghĩa là địa phương hóa của $\mathbf{DM}_{gm}^{eff}(k)$ theo các Tate motive $\mathbb{Z}(n)$.

 

Ở đây mình định nghĩa một cách tricky (dựa trên một định lý) đồng điều Suslin.

 

Định nghĩa (đồng điều Suslin+đối đồng điều motivic) Đồng điều Suslin $H^{Sus}_i(X)$ của một lược đồ trơn $X$ được định nghĩa bởi

$$H^{Sus}_i(X) = \mathrm{Hom}_{\mathbf{DM}^{eff}_{gm}}\left(\mathbb{Z}[i], M_{gm}(X) \right).$$

Đối đồng điều motivic là phiên bản xoắn + phản biến của đồng điều Suslin

$$H^p(X,\mathbb{Z}(q)) = \mathrm{Hom}_{\mathbf{DM}^{eff}_{gm}} \left(M_{gm}(X), \mathbb{Z}(q)[p] \right).$$

Dưới đây là một số tính chất đối đồng điều motivic.

Tồn tại tích cup .$H^p(X,\mathbb{Z}(q)) \otimes H^{p'}(X,\mathbb{Z}(q')) \to H^{p+p'}(X,\mathbb{Z}(q+q'))$ bằng cách gửi $a \otimes b$ thông qua dãy hợp thành

$$M_{gm}(X) \overset{\delta}{\rightarrow} M_{gm}(X) \otimes M_{gm}(X) \overset{a \otimes b}{\rightarrow} \mathbb{Z}(q)[p] \otimes \mathbb{Z}(q')[p'] \cong \mathbb{Z}(q+q')[p+p'].$$

Thỏa mãn tính $\mathbb{A}^1$-đồng luân, i.e. $p^*: H^p(X,\mathbb{Z}(q)) \overset{\sim}{\rightarrow} H^p(X \times \mathbb{A}^1_k,\mathbb{Z}(q)).$

 

Dãy Mayer-Vietoris. Nếu $U, V \subset X$ là hai tập mở thì ta có dãy Mayer-Vietoris:

$$... \to H^{p-1}(U \cap V, \mathbb{Z}(q)) \to H^p(U \cup V, \mathbb{Z}(q)) \to H^p(U,\mathbb{Z}(q)) \oplus H^p(V,\mathbb{Z}(q)) \to H^p(U\cap V, \mathbb{Z}(q)) \to ...$$

Recover lại một số đối đồng điều cổ điển.Ví dụ $H^1(X,\mathbb{Z}(1))= \Gamma(X,\mathcal{O}_X^{*}), H^2(X,\mathbb{Z}(1)) = H^1(X,\mathcal{O}_X^*)$ và do đó ta có thể định nghĩa lớp Chern của một phân thớ đường $L$ bởi phần tử $[L]$ tương ứng trong $H^2(X,\mathbb{Z}(1))$.

Đã rất lâu kể từ khi Grothendieck giới thiệu lý thuyết lược đồ (scheme theory) trong bộ "Éléments de géométrie algébrique" thì tới nay lược đồ đã trở thành một ngôn ngữ cơ bản của hình học đại số và có ứng dụng sâu rộng trong những ngành liên quan như lý thuyết số.

 

The very notion of a scheme has a childlike simplicity - so simple, so humble in fact that no one before me had the audacity to take it seriously.

 

Nó đã một lần và mãi mãi thay đổi hình học đại số thành một ngôn ngữ quá sức trừu tượng với bất cứ ai, nhất là những ai không có khả năng về đại số (David Mumford từng viết một bài "Có thể giải thích lý thuyết lược đồ cho một nhà sinh học không?") vì một lý do đơn giản, nó dựa rất nặng trên ngôn ngữ đại số giao hoán. Ngày nay không ai có thể học hình học đại số mà không học ngày càng nhiều đại số giao hoán. Vào thời kỳ mà lý thuyết lược đồ mới bắt đầu, nó đã làm "sấp ngửa" các nhà toán học. David Mumford từng viết

 

Then Grothendieck came along and turned a confused world of researchers upside down, overwhelming them with the new terminology of schemes as well as with a huge production of new and very exciting results. These notes attempted to show something that was still very controversial at that time: that schemes really were the most natural language for algebraic geometry and that you did not need to sacrifice geometric intuition when you spoke "scheme".

 

Thậm chí ngay cả P. Cartier, một người mà Grothendieck đặc biệt ngưỡng bộ về tốc độ học những thứ mới cũng phải kêu lên rằng hình học đại số có ba cuộc lột xác và ông phải học kiến thức mới qua cả ba lần đó: đầu tiên bắt từ trường phái Ý, sau đó đến Serre và cuối cùng nó hoàn toàn thay đổi sau Grothendieck.

 

Ngày nay, có vô vàn sách về hình học đại số được viết dưới các ngôn ngữ rất trừu tượng và thông thường sinh viên đại học phải có một lượng kiến thức chuẩn bị cực kỳ lớn để thực sự hiểu được cái đẹp của hình học đại số, rằng nó thực sự là hình học chứ không phải chỉ là một loạt các định nghĩa vô cùng trừu tượng từ trên trời rơi xuống. Nhưng đó là cản trở đầu tiên của bất cứ sinh viên nào muốn tiếp cận hình học đại số: người ta phải sẵn sàng lao thân vào một vũng bùn trước khi sang được bờ bên kia.

 

Bài viết này của mình là một dẫn nhập không chính thức (informal) cho các bạn sinh viên nào muốn tiếp cận hình học đại số mà vẫn loay hoay với lý thuyết lược đồ. Do đó không thực sự có định nghĩa, không thực sự có chứng minh, chỉ là các bàn luận và chỉ ra rằng rất nhiều thứ trong hình học đại số có động lực từ hình học và tô-pô. Nó cũng không phải một bài viết mang tính lịch sử, tức là thảo luận tiến trình phát triển hình học đại số và lý thuyết số mà mình sẽ viết, theo cách nào đó để người mới tiếp cận cảm thấy lý thuyết này tự nhiên nhất và xây dựng cho bản thân một trực giác để có thể học dễ dàng hơn; do đó không tránh khỏi việc có những thứ mang tính "đoán". Khi hỏi bất cứ ai làm hình học đại số câu hỏi "hình học đại số là gì?" nhiều khả năng bạn sẽ nhận được câu trả lời "là một ngành nghiên cứu nghiệm của các phương trình" nhưng nếu bạn mở các sách hình học đại số ra thì nhận được toàn là "vành địa phương chính quy", "bó tựa nhất quán", "đối đồng điều",... Vậy chúng ta hãy quay lại câu hỏi về việc giải phương trình, một trong các nguồn gốc đầu tiên cho hình học đại số hiện đại đến từ lý thuyết số: bài toán giải các phương trình nghiệm nguyên.

 

Phương trình nghiệm nguyên tới số nguyên p-adic

 

Giả sử ta có một phương trình

$$F(x_1,...,x_n) = 0$$

trong đó $F \in \mathbf{Z}[x_1,...,x_n]$ là một đa thức với hệ số nguyên và ta được yêu cầu tìm các nghiệm nguyên (tương đương, hữu tỷ) của nó. Câu hỏi này thông thường là quá khó để giải và nó chính là bài toán thứ $10$ của Hilbert. Câu trả lời khá dễ đoán: không tồn tại một cách giải tổng quát một phương trình cho trước. Do đó chúng ta có thể thử làm yếu bài toán, giải một phương trình như trên trong modulo $m$ nào đó, tức là

$$F(x_1,...,x_n) = 0 \ \mathrm{mod} \ m$$ liệu có nghiệm modulo $m$ không. Bằng định lý thặng dư Trung Hoa, ta quy về giải các phương trình

$$F(x_1,...,x_n) = 0 \ \mathrm{mod} \ p^v$$ trong đó $p$ là một số nguyên tố. Đây là chỗ các số $p$-adic nhảy vào cuộc chơi (các bạn có thể xem lại bài này của anh @nmlinh16).

 

 

Trong bài viết đó anh nmlinh16 đã thử giải phương trình $x^2+1$ modulo $5$ và nói rằng cách giải này là địa phương. Trước tiên nhắc lại một số nguyên $p$-adic là một tổng hình thức (tức là chưa nói đến việc nó hội tụ theo nghĩa nào)

$$a_0 + a_1p + \cdots + a_n p^n + \cdots$$ với $0 \leq a_i <p$ là các số nguyên. Ký hiệu tập số nguyên $p$-adic bởi $\mathbf{Z}_p$. Tương tự, các số hữu tỷ $p$-adic có dạng hình thức

$$a_{-m}p^{-m} + \cdots + a_{-1}p^{-1} + a_0 + a_1p + a_2p^2 +\cdots$$ với $0\leq a_i < p$ là các số nguyên; viết khác đi $a_i \in \mathbf{Z}/p$. Tập này được ký hiệu bởi $\mathbf{Q}_p$. Cả hai tập này đều là các vành. Điều này gợi nhớ các bạn đã học giải tích phức về khái niệm chuỗi và chuỗi Laurent

$$a_{-m}(x-a)^{-m} + ...+ a_{-1}(x-a)^{-1} + a_0 + a_1(x-a) + \cdots + a_n(x-a)^n + \cdots$$

Ta có thể nói gọn rằng một số nguyên $p$-adic là một xấp xỉ bởi các đa thức tổng riêng

$$S_n=a_0 + a_1p + \cdots a_n p^n$$

Nhưng như thế chưa thực sự đủ, ta hãy nhớ rằng mỗi $S_n$ xác định một lớp dư $\overline{S_n}$ trong $\mathbf{Z}/p^n$. Do đó một số nguyên $p$-adic xác định một dãy

$$(S_0,S_1,...,S_n,...) \in \prod_{i=0}^{\infty}(\mathbf{Z}/p^n).$$

Tuy nhiên hãy nhớ ta đang nói về tính xấp xỉ, mỗi một $S_n$ còn "thừa" ra một hệ số $a_n$ so với $S_{n-1}$. Tuy nhiên rất may ta có thể lưu hệ số này bằng phương trình $S_n = S_{n-1} \ \mathrm{mod} \ p^{n-1}$. Bằng cách này, ta viết rằng

$$\mathbf{Z}_p = \lim \mathbf{Z}/p^n = \left \{(x_n)_{n \in \mathbf{N}} \in \prod_{n=0}^{\infty}(\mathbf{Z}/p^n) \mid x_{n+1}=x_n \ \mathrm{mod} \ \mathbf{Z}/p^n \right \}.$$

Ta sẽ gặp lại biểu diễn này ở bài dưới. Trước tiên ta có mệnh đề sau.

 

Mệnh đề. Phương trình $F(x_1,...,x_n)=0 \ \mathrm{mod} \ p^v$ có nghiệm với $v\geq 1$ bất kỳ khi và chỉ khi $F(x_1,...,x_n)=0$ có nghiệm trong $\mathbf{Z}_p$.

 

Người ta bảo đây là tìm nghiệm "địa phương", nhưng thế nào là địa phương (local). Địa phương là một khái niệm rất có tính hình học và tô-pô. Để nói về địa phương thì bạn phải có điểm, và lân cận. Và quan trọng hơn tất cả các thứ đó, bạn phải có một không gian. Cái không gian mà chúng ta nói đến đây, chính là các lược đồ.

 

Hãy quay lại với các phương trình vi phân. Việc giải một phương trình vi phân $Df=0$ trên một đa tạp $M$ (với những bạn chưa biết về đa tạp, có thể giả sử đang giải trên toàn trục $\mathbf{R}$) có thể được thực hiện một cách ngây thơ như sau:

• (Bước 1) Cố gắng thu nhỏ khoảng xác định, tìm nghiệm quanh các lân cận đủ nhỏ. Các nghiệm này gọi là nghiệm địa phương.
• (Bước 2) Cố gắng dán các nghiệm địa phương thành một nghiệm toàn cục.

Như vậy khi nói việc giải nghiệm $p$-adic là giải địa phương, một cách hình thức, ta đã tiền giả định các điều sau:

• Tồn tại một không gian tô-pô $X$ mà số nguyên tố $p$ là một "điểm" của $X$.
• Quá trình giải nghiệm $p$-adic thực chất đang làm việc trên một lân cận của $p$ trong $X$.

Các không gian $X$ này được ký hiệu bởi $\mathrm{Spec}(\mathbf{Z})$, là một ví dụ của lược đồ affine. Tổng quát hơn, ta muốn hỏi rằng với mỗi vành giao hoán có đơn vị $R$, làm thế nào để xây dựng một lược đồ $\mathrm{Spec}(R)$?

 

Nghiệm nguyên - một góc nhìn khác

 

Trong phần này, mình giả sử các bạn đã biết về định nghĩa vành và đồng cấu vành. Toàn bộ các vành được giả sử là giao hoán và có đơn vị. Cho $R$ là một vành, khi đó một $R$-đại số là một đồng cấu vành $R \longrightarrow A$. Điều này có nghĩa:

• Bản thân $A$ là một vành: có phép cộng và nhân.
• Có thể nhân vô hướng $R$ với $A$: mỗi cặp $(r,a) \in R \times A$ xác định một phần tử $ra \in A$.

Một đồng cấu $\phi: A \longrightarrow B$ của hai $R$-đại số là một đồng cấu vành sao cho $\phi(ra)=r\phi(a)$ (điều này giống với định nghĩa của không gian vector). Ta gọi $A$ là có kiểu hữu hạn trên $R$ tồn tại một tập hữu hạn các phần tử $a_1,...,a_n \in A$ sao cho mọi phần tử trong $A$ có dạng

$$\sum r_{i_1,...,i_k} a_1^{i_1}\cdots a_n^{i_n}$$ với $i_1,...,i_n$ là các số nguyên không âm và $r_{i_1,...,i_k}$ là phần tử trong $R$. Nói cách khác, mọi phần tử của $A$ là "một đa thức". Điều này khác với việc nếu bạn xét một không gian vector hữu hạn sinh $V$ (do đó hữu hạn chiều) trên một trường $k$ (bạn có thể lấy $k = \mathbf{R}$ hoặc $\mathbf{C}$), khi đó mọi vector $v$ có dạng

$$v = k_1v_1 + \cdots k_n v_n,$$ trong đó $k_i$ là các vô hướng và $v_i$ là các vector lập thành một hệ sinh. Khác biệt này đến từ việc không gian vector chỉ có phép nhân vô hướng, nó không có phép nhân trong (cái cấu thành các phần tử dạng $a_1^{i_1}$). Hệ $\left \{a_1,...,a_n \right \}$ đóng vai trò một hệ sinh cho đại số như cái cách mà một hệ sinh của không gian vector làm. Nói tương đương, tồn tại một toàn cấu của các $R$ -đại số

$$R[x_1,...,x_n] \longrightarrow A$$

và nói cách khác nữa $A$ có dạng $R[x_1,...,x_n]/I$ với $I$ là một ideal của $R[x_1,...,x_n]$. Không giảm tổng quát, ta giả sử $I$ là hữu hạn sinh, tức là $I$ sinh ra bởi hữu hạn đa thức $f_1,...,f_r$ và do đó

$$A = R[x_1,...,x_n]/(f_1,...,f_r).$$ Trong đại số tuyến tính, ta biết rằng một đồng cấu tuyến tính xác định duy nhất bởi ảnh trên các phần tử của một cơ sở. Tương tự ở đây ta có một đồng cấu các $R$-đại số xác định duy nhất bởi tập ảnh của các phần tử sinh và tuân theo quan hệ mà các phần tử sinh tuân theo.

 

Bổ đề. Các đồng cấu giữa hai $R$-đại số $R[x_1,...,x_n]/(f_1,...,f_r) \longrightarrow B$ song ánh với tập $$\left \{(b_1,...,b_n) \in B^n \mid f_i(b_1,...,b_n) \right \}.$$ Hay nói cách khác, nó tương đương với tập nghiệm của hệ phương trình $\left \{f_1=...=f_r =0 \right \}.$

 

Thế thì ví dụ việc bạn muốn giải một phương trình nghiệm nguyên kiểu $y^2 = x^3 + x + 1$ thì tương đương với việc bạn muốn tìm các đồng cấu của các $\mathbf{Z}$-đại số

$$\mathbf{Z}[x,y]/(y^2-x^3-x-1) \longrightarrow \mathbf{Z}.$$ Lưu ý rằng hợp thành của một đồng cấu như vậy với đồng cấu hiển nhiên $\mathbf{Z} \longrightarrow \mathbf{Z}[x,y]/(y^2-x^3-x-1)$ là đồng nhất. Điều này cộng với phần trước gợi ý cho ta một hình dung đầu tiên về một lược đồ affine:

• Một lược đồ affine của một vành $R$ là một không gian tô-pô $\mathrm{Spec}(R)$ và ta không mất gì khi nghiên cứu $\mathrm{Spec}(R)$ thay vì $R$. Tức là tồn tại một xây dựng ngược $\mathrm{Spec}(R) \mapsto R$ và quan trọng hơn xây dựng này có tính hàm tử như dưới đây.
• Mỗi đồng cấu vành $R \longrightarrow R'$ cho ta một ánh xạ liên tục $\mathrm{Spec}(R') \longrightarrow \mathrm{Spec}(R)$ (well, ở bước này bạn có thể hỏi rằng tại sao nó không đi theo chiều ngược lại).
• Nếu $R'$ là một $R$-đại số hữu hạn sinh dạng $R[x_1,...,x_n]/(f_1,...,f_r)$ thì việc nghiên cứu hệ phương trình $\left \{f_1=...=f_r \right \}$ tương được với việc tìm các "ánh xạ liên tục" $\mathrm{Spec}(R) \longrightarrow \mathrm{Spec}(R[x_1,...,x_r]/(f_1,...,f_r))$ sao cho hợp thành với $\mathrm{Spec}(R[x_1,...,x_r]/(f_1,...,f_r))$ là đồng nhất. Hay ta còn gọi một bộ nghiệm là một nhát cắt (section). Thuật ngữ này mang tính hình học. Một nhát cắt của một ánh xạ liên tục $f: X \longrightarrow Y$ là một cách "đi ngược lại" từ $Y$ vào $X$. Cụ thể hơn là tồn tại $s: Y \longrightarrow X$ liên tục mà $f \circ s = \mathrm{id}_Y$. Xem hình dưới

 

Cái mà mình vừa trình bày đây, gọi là khái niệm hàm tử điểm (functor of points) của Grothendieck.

 

 

Lược đồ - một gợi ý từ định lý biểu diễn Gelfand

 

Cho $X$ là một không gian tô-pô (với các bạn sinh viên năm nhất có thể lấy $X$ là không gian metric). Khi đó không gian các hàm liên tục

$$C(X,\mathbf{R}) = \left \{f: X \longrightarrow \mathbf{R} \mid f \ \text{liên tục} \ \right \}$$

là một vành giao hoán có đơn vị là hàm hằng $1$. Tức là có phép cộng và phép nhân theo từng điểm

$$(f+g)(x) = f(x) + g(x) \ \ \ \ \text{và} \ \ \ \ (f.g)(x) = f(x)g(x)$$

và thậm chí nó còn có một phép nhân vô hướng (tuy nhiên ta không cần tới như vậy). Một bài toán cơ bản trong tô-pô là phân loại các không gian chính xác tới một đồng phôi. Một trong các cách làm thông thường mà ta hay làm là gán một không gian $X$ với một bất biến đại số $X$ được bảo toàn bởi phép đồng phôi. Phép gán $X \mapsto C(X,\mathbf{R})$ là phép gán có thể nói là ngây thơ nhất.

 

Bây giờ ta hãy lấy slogan sau làm định hướng cho các thảo luận tiếp
 

 

Slogan. Một không gian đủ tốt "nên" được nghiên cứu bằng cách "nghiên cứu" tất cả các hàm trên nó.

 

 

Vành $C(X,\mathbf{R})$ có tính chất gì đặc biệt và nó liên hệ thế nào với $X$? Ít nhất nó thỏa mãn các tính chất sau:

• Với mỗi tập mở $U \subset X$ ta có một vành $C(U,\mathbf{R})$. Với hai tập mở $V \subset U$ ta có một phép hạn chế $C(U,\mathbf{R}) \longrightarrow C(V,\mathbf{R})$ đi từ tập to hơn xuống tập nhỏ hơn. Do một hàm xác định trên tập to thì cũng xác định trên tập nhỏ.
• Với mọi $f \in C(X,\mathbf{R})$ thì tập $U_f=\left \{x \in X \mid f(x) \neq 0 \right \}$ là một tập mở trong $X$ và $f$ hạn chế xuống tập này là một phần tử khả nghịch của $C(U_f,\mathbf{R})$. Nói cách khác, ảnh của $f$ thông qua ánh xạ hạn chế $C(X,\mathbf{R}) \longrightarrow C(U_f,\mathbf{R})$ là một phần tử khả nghịch.
• Ngược lại thì tập $X \setminus U_f = \left \{x \in X \mid f(x) = 0 \right \}$ là tập đóng. Các tập đóng này sinh ra tô-pô trên $X$ nếu $X$ là compact và Hausdorff (bổ đề Uryson).
• Với mọi $x \in X$ thì tập $\mathfrak{m}_x=\left \{f \in C(X,\mathbf{R}) \mid f(x) = 0 \right \}$ là một ideal của $X$. Hơn nữa nó còn là ideal cực đại do $C(X,\mathbf{R})/\mathfrak{m}_x \simeq \mathbf{R}$ là một trường.
• Tập $\mathrm{Max}(C(X,\mathbf{R})) = \left \{\mathfrak{m}_x \mid x \in X \right \}$ được trang bị một tô-pô gọi là tô-pô Zariski. Ta định nghĩa nó thông qua các tập đóng $$V(I) = \left \{\mathfrak{m} \in \mathrm{Max}(C(X,\mathbf{R})) \mid I \subset \mathfrak{m} \right \}.$$ Tập này còn gọi là phổ cực đại (chứa các ideal cực đại) của $C(X,\mathbf{R})$. Tương tự, mọi vành $R$ cho ta một không gian tô-pô $\mathrm{Max}(R)$.

Định lý sau, được biết tới tên định lý biểu diễn Gelfand (xem chứng minh ở đây) là minh chứng cho slogan trên.

 

Định lý. Nếu $X$ là một không gian tô-pô compact và tách được thì phép gán $X \mapsto \mathrm{Max}(C(X,\mathbf{R})), x \longmapsto \mathfrak{m}_x$ là một đồng phôi.

 

Như vậy khi ta có một phép gán

$$\text{không gian tô-pô} \longmapsto \text{vành} \longmapsto \text{không gian tô-pô}$$ và ta chứng minh rằng với không gian đủ tốt thì ta không mất gì cả, vẫn luôn thu được không gian ban đầu. Như vậy, nó dẫn ta tới một câu hỏi ngược lại: cho một vành $R$ (kể từ nay luôn luôn giao hoán và có đơn vị), làm thế nào mà mỗi phần tử $r \in R$ có thể xem như một hàm trên một không gian tô-pô $\mathrm{Spec}(R)$ nào đó mà nó có tất cả các tính chất tương tự như những gì $C(X,\mathbf{R})$ có? Tuy nhiên bất kể nó là cái gì, ta không nên sử dụng xây dựng phổ cực đại $\mathrm{Max}(R)$ vì rất nhiều lý do:

• Có những vành rất thú vị mà lại có quá ít ideal cực đại (một vành chỉ có một ideal cực đại gọi là vành địa phương).
• Tô-pô Zariski quá xấu để nói về tính liên tục.
• Xây dựng $\mathrm{Max}(R)$ không có tính "hàm tử", một đồng cấu vành $\phi:R \longrightarrow R'$ không cho ta một ánh xạ $\mathrm{Max}(R') \longrightarrow \mathrm{Max}(R)$ bằng phép nghịch đảo $I \mapsto \phi^{-1}(I)$ vì nghịch đảo một ideal cực đại không nhất thiết là ideal cực đại.
• Xây dựng $\mathrm{Max}(R)$ không nhìn được "bội". Ví dụ nghiên cứu hai vành $\mathbf{C}[x]/(x)$ và $\mathbf{C}[x]/(x^2)$ như đã nói trong phần trước tương đương với việc ta giải hai phương trình $\left \{x=0 \right \}$ và $\left \{x^2=0 \right \}$. Về mặt tập nghiệm, chúng trùng nhau. Tuy nhiên về mặt bội thì không. Nghiệm đầu tiên $x=0$ là nghiệm đơn nằm trên một đường thẳng $y=x$. Nghiệm sau đó $x=0$ là nghiệm kép nằm trên một parabol $y=x^2$.

Tuy nhiên, dù thế nào ta cũng đã đến gần với lời giải. Giờ ta nhớ rằng để nói về hàm số, ta phải nói về cái là điểm. Một hàm sinh ra là để tính giá trị trên các điểm. Nếu không có điểm thì không có hàm. Nói cách khác, ta phải xem tập nền (nếu có) của $\mathrm{Spec}(R)$ là gì? Các phần tử của nó (các điểm) được tính giá trị như thế nào.

 

Slogan. Để có hàm thì phải có điểm. Một khi có điểm, hàm được xác định duy nhất bằng các giá trị.

 

 

Ở đây, "không biết bằng cách nào" mà André Martineau lại xúi Jean Pierre Serre rằng nên lấy các ideal nguyên tố làm tập nền cho $\mathrm{Spec}(R)$.

 

Định nghĩa. Với mỗi vành $R$, lược đồ affine $\mathrm{Spec}(R)$ có tập hợp nền là tập các ideal nguyên tố $\mathfrak{p}$ của $R$.

 

Như vậy với mỗi $f \in R$ có thể xem như một hàm trên $\mathrm{Spec}(R)$ và với mỗi ideal nguyên tố $\mathfrak{p} \in \mathrm{Spec}(R)$ thì ta có một giá trị $f(\mathfrak{p})$ (mà ta chưa biết tập giá trị là gì). Hơn nữa, việc gán

$$f \longmapsto \left \{f(\mathfrak{p}) \mid \mathfrak{p} \in \mathrm{Spec}(R) \right \}$$

xác định duy nhất $f$. Vậy vấn đề bây giờ còn lại là xác định miền giá trị của $f(\mathfrak{p})$.

 

Ta hãy quay lại với các ví dụ cụ thể hơn:

• Khi $R = \mathbf{C}[x]$ là vành đa thức. Do $\mathbf{C}$ là đóng đại số nên các ideal nguyên tố khác $0$ của $\mathbf{C}[x]$ cũng cực đại và có dạng $(x-a)$ với $a \in \mathbf{C}$. Ta mong muốn có một phép gán mỗi đa thức $f$ thành $$f:\mathrm{Spec}(\mathbf{C}[x]) = \left \{(0) \right \} \cup \bigcup_{a \in \mathbf{C}} (x-a).$$ Tuy nhiên phải nói thế nào về việc tính $f((x-a))$? Hiển nhiên mỗi đa thức là một hàm (theo nghĩa giải tích) $f: \mathbf{C} \longrightarrow \mathbf{C}$ và do đó nên có $f((x-a))=f(a)$. Nhưng có cách nào khác nhìn $f(a)$ không? Rất may mắn ta có $f = f(a) \mathrm{mod} \ (x-a)$. Nói cách khác, mỗi hàm $f$ xác định các giá trị trong các vành thương $\mathbf{C}[x]/(x-a)$, chúng là các trường. Vấn đề còn lại là làm sao xác định $f((0))$? Vành thương $\mathbf{C}[x]/(0) = \mathbf{C}[x]$ không là một trường, làm thế nào để tạo ra một trường, xem như trường giá trị. Rất đơn giản và thần kỳ, ta lấy trường các hàm hữu tỷ $C(x)$ (phần tử là thương hai đa thức) và xem $f$ như một phần tử trong trường này.
• Khi $R = \mathbf{Z}$ là vành số nguyên. Các ideal nguyên tố của $R$ hoặc là các số nguyên tố $p$ hoặc là ideal tầm thường $0$. Tương tự như trên một số nguyên $n$ tính giá trị tại một ideal nguyên tố bằng cách tính modulo $p$, tức là $(n \ \mathrm{mod} \ p)$, giá trị này nằm trong trường $\mathbf{Z}/p$. Còn $n$ tính giá trị tại ideal $0$ là việc ta xem $n$ như một phần tử trong $\mathbf{Q}$ (thương của hai số nguyên).

Điều này cho ta một gợi ý về mặt tổng quát: ta nên lấy giá trị $f(\mathfrak{p})$ nằm trong trường các thương $\mathrm{Frac}(R/\mathfrak{p})$. Do đó công thức hoàn chỉnh của ta là

$$f : \mathrm{Spec}(R) \longrightarrow \bigsqcup f(\mathfrak{p}) \in \bigsqcup \mathrm{Frac}(R/\mathfrak{p}).$$

 

Tô-pô của $\mathrm{Spec}(R)$ trông như thế nào?

 

Nhắc lại rằng khi nói về $C(X,\mathbf{R})$, ta thấy các tập

$$\left \{x \in X \mid f(x) \neq 0 \right \}$$

là các tập mở trong $X$ chừng nào $f$ khác $0$ (nếu không tập này rỗng, vẫn mở, nhưng tầm thường). Tương tự như vậy ta muốn các tập

$$D(f) = \left \{\mathfrak{p} \in \mathrm{Spec}(R) \mid f(\mathfrak{p}) \neq 0 \right \}$$

là các tập mở trong $\mathrm{Spec}(R)$ với mỗi $f$ cố định. Hơn nữa, ta còn muốn nó là một cơ sở tạo nên tô-pô của $\mathrm{Spec}(R)$. Trước tiên ta nhắc lại rằng trong trường hợp $C(X,\mathbf{R})$ (tức là $R$) trong trường hợp đại số này) với mỗi tập mở $U$ của $X$ (các tập mở $D(f)$ của $\mathrm{Spec}(R)$) ta có một vành $C(U,\mathbf{R})$ và vành này lại lần nữa xác định duy nhất $U$ (nếu $U$ đủ tốt). Vậy ta có thể tự hỏi, nếu có thể thì cái gì sẽ đóng vai trò của $C(U,\mathbf{R})$ trong trường hợp này?

$$U \longmapsto C(U,\mathbf{R}) \Longrightarrow D(f) \longmapsto ???.$$

Tức là có vành $R_f$ nào mà $\mathrm{Spec}(R_f) = D(f)$ không?

 

Câu trả lời là có, đây là khái niệm địa phương hóa. Ý tưởng của nó như sau: nếu $f \in R$ là một hàm, thì trên tập $D(f)$ hàm $f$ phải khả nghịch. Nói cách khác, phải có một đồng cấu vành $R \longrightarrow R_f$ mà ảnh của $f$ khả nghịch (giống như trường hợp $C(X,\mathbf{R}) \longrightarrow C(U,\mathbf{R})$). Như ở đây ta còn chưa khai thác hết, tập $\left \{x \in X \mid f(x) \neq 0 \right \}$ thực sự là tập lớn nhất mà $f$ khả nghịch nên theo nghĩa nào đó đồng cấu $C(X,\mathbf{R}) \longrightarrow C(U,\mathbf{R})$ là đồng cấu nhỏ nhất làm $f$ khả nghịch. Như vậy ta phải tạo ra một vành $R_f$ càng nhỏ càng tốt mà $f$ khả nghịch.

 

Thế nào là nhỏ nhất? Nó có nghĩa là nếu $R \longrightarrow S$ là một đồng cấu vành mà $f$ khả nghịch thì nó tách qua $R \longrightarrow R_f$. Ở dạng biểu đồ giao hoán:

\begin{xy}
\xymatrix {
 R  \ar[r] \ar[dr]& R_f \ar[d] \\
& S
}
\end{xy}

 

Đây là định nghĩa có thể "làm sợ" các bạn lần đầu học đại số giao hoán. Nó gọi là khái niệm địa phương hóa. Tại sao lại là địa phương? (lưu ý rằng địa phương này của hàm, nó hơi khác với lời hứa ở đầu bài của mình, đó là địa phương hóa điểm) Vì ta đang hạn chế làm việc ở lân cận mà hàm $f$ khả nghịch (lưu ý ta đang giả sử $f$ khác $0$).

 

Xây dựng $R_f$: Ta xét tập hợp $\left \{(r,f^n) \mid r \in R, n \in \mathbf{Z} \right \}$ và ta định nghĩa một quan hệ tương đương $(r,f^n) = (r',f^m)$ nếu tồn tại $k \in \mathbf{Z}$ mà $f^{k-m}r = f^{k-n}r'$. Ai tinh ý sẽ nhận ra đang giả vờ rằng $(r,f^n)$ chính là một phân số $\frac{r}{f^n}$. Điều này giống như ta định nghĩa số hữu tỷ $\mathbf{Q}$. Ta nói $(a,b)=(c,d)$ (ngầm hiểu $a/b = c/d$) nếu $ad=cb$. Tuy nhiên ở đây ta phải nhân thêm $f^k$ vì nếu không nó không là quan hệ tương đương. Còn trên $\mathbf{Q}$ là miền nguyên thì ta có thể khử phần tử khác $0$ trong phép nhân nên mọi chuyện tầm thường. Vì lý do này mà ta còn viết $R_f$ dưới dạng vành đa thức $R[\frac{1}{f}]$.

 

Tới đây ta đã hoàn thành kha khá về bức tranh của $\mathrm{Spec}(R)$: tô-pô của nó có một cơ sở sinh bởi các tập $D(f)$ và các hàm trên $D(f)$ là $R_f$ (lưu ý rằng $R = R_1$ với $1 \in R$ là hàm hằng). Ta lại quay lại với $C(X,\mathbf{R})$. Như đã nói ban đầu, ta đã gian lận, ta đã xem xét tô-pô Zariski (với phổ cực đại) trên vành này ngay từ đầu. Bây giờ ta cần kiểm tra xem hai tô-pô sau có trùng nhau không:

• Tô-pô sinh bởi các tập $D(f)$.
• Tô-pô Zariski của $\mathrm{Spec}(R)$, tức là các tập đóng có dạng $V(I) = \left \{\mathfrak{p} \in \mathrm{Spec}(R) \mid f(\mathfrak{p}) = 0 \right \}$ với $I$ là một tập con bất kỳ của $R$.

Không nghi ngờ gì là có dù ta đang dùng hai ngôn ngữ khác nhau: tập mở và tập đóng, lần lượt. Lưu ý rằng

$$D(f) = \left \{f \neq 0 \right \} = X \setminus V(f) = X \setminus \left \{f = 0 \right \} \ \ \ \ \text{và} \ \ \ \ V(I) = \bigcup_{f \in I} V(f).$$

Như vậy ta có điều phải chứng minh (hai tô-pô trùng nhau nhưng góc nhìn thì thêm nhiều điểm mới).

Lân cận của điểm

 

Giờ đây ta biết số nguyên tố $p$ xác định một ideal nguyên tố $(p)$, và do đó là điểm $(p) \in \mathrm{Spec}(\mathbf{Z})$. Một lân cận của $(p)$ thì trông như thế nào?

 

Ta biết rằng cơ sở của tô-pô Zariski là các tập $D(n)$ với $n \in \mathbf{Z}$. Như vậy nếu $(p) \notin D(n)$ thì có nghĩa là

$$n((p)) = 0 \Leftrightarrow n = 0 \ \mathrm{mod} \ p \Leftrightarrow p \mid n.$$

Điều này cũng trực tiếp suy ra mỗi hàm $n \in \mathbf{Z}$ chỉ triệt tiêu tại hữu hạn điểm (giống như một đa thức chỉ có hữu hạn nghiệm). Nói cách khác tập $D(n)$ là là kỳ cục, nó là phần bù của một tập hữu hạn không chứa $(0)$ trong $\mathrm{Spec}(\mathbf{Z})$, i.e. có dạng

$$\mathrm{Spec}(\mathbf{Z}) - \left \{(p_1),...,(p_r) \right \}$$

nếu $\left \{p_1,...,p_r \right \}$ là tập các ước nguyên tố của $n$. Nói cách khác, dù họ $D(n)$ là một cơ sở cho tô-pô. Nhưng các phần tử của cơ sở này không tốt chút nào: CHÚNG KHÔNG NHỎ, HAY CÒN RẤT TO LÀ KHÁC! (mọi tập $D(n)$ đều trù mật trong $\mathrm{Spec}(\mathbf{Z})$)Thêm một tính chất nữa, trong không gian Hausdorff, nếu bạn lấy giao tất cả các lân cận của một điểm thì bạn thu được chính điểm đó. Giờ nếu ta lấy giao

$$\bigcap_{(p) \in D(n)} D(n)$$

thì ta thu được cái gì? Hãy viết cái này dưới dạng thân thương hơn

$$\bigcap_{n \notin (p)} \left \{n \neq 0 \right \}.$$

Để nói rằng giao này không hề nhỏ, ta hãy nhìn vào các hàm trên nó, hãy tự thuyết phục bản thân bạn rằng các hàm trên nó là cái gì đó như thế này

$$\bigcup_{n \notin (p)} \mathbf{Z}\big[\frac{1}{n}\big].$$

Trong đó hợp này giao được lấy trong một tập to hơn, dễ nhất là lấy trong $\mathbf{Q}$. Tới đây, ta thu được một vành "khá to", nó là địa phương hóa $\mathbf{Z}_{(p)}$ của $\mathbf{Z}$ tại ideal $(p)$. Ở dạng tập hợp, như trên đã gợi ý, nó chính là

$$\mathbf{Z}_{(p)} = \left \{\frac{n}{m} \in \mathbf{Q} \mid p \nmid m \right \}.$$

Như vậy ít nhất nó trái với trực giác chúng ta là hàm trên không gian một điểm thì toàn là tầm thường. Các hàm trong tập $\mathbf{Z}_{(p)}$ trái lại chẳng có vẻ tầm thường chút nào. Chẳng hạn thay vì $\mathbf{Z}$ bạn hãy nhìn vào vành $\mathbf{C}[x]$ và lấy giao tất cả các lân cận của điểm $(x-a)$ thì các bạn nhận được là gì? Nó chính là các hàm hữu tỷ $\frac{f(x)}{g(x)}$ mà $g(a) \neq 0$ (viết cách khác $g((x-a)) \neq 0$, giống như $\frac{n}{m} \in \mathbf{Q}$ với $m((p)) \neq 0$). Mỗi hàm hữu tỷ như vậy đều có khai triển Taylor tại $x=a$ ở dạng

$$\frac{f(x)}{g(x)} = a_0 + a_1(x-a) + a_2(x-a)^2 + \cdots + a_n(x-a)^n + \cdots \ a_i \in \mathbf{C}=\mathbf{C}[x]/(x-a)$$

và do đó bạn đoán rằng các số hữu tỷ trong tập $\mathbf{Z}_{(p)}$ cũng phải có dạng

$$\frac{n}{m} = a_0 + a_1p + a_2p^2 + \cdots + a_n p^n + \cdots \ a_i \in \mathbf{Z}/p,$$

tức là các hệ số thực chất chỉ cần lấy trong tập $\left \{0,1,...,p-1 \right \}$. Đây là ví dụ đầu tiên về số $p$-adic một cách hình học. Nhưng thực chất, tập $\mathbf{Z}_{(p)}$ chưa vét cạn các số nguyên $p$-adic.

 

Tuy nhiên ta hãy dành nó cho phần sau. Ở đây từ các suy luận trên ta thấy rằng với mỗi điểm $\mathfrak{p} \in \mathrm{Spec}(R)$ thì ta có một vành $R_{\mathfrak{p}}$ là vành địa phương (chỉ có một ideal cực đại). Đến đây ta tạm gọi là đã vẽ được phần nào bức tranh về lược đồ affine

$$((R,\mathrm{Spec}(R)), (R_f,D(f)), (R_{\mathfrak{p}},\bigcap_{\mathfrak{p} \in D(f)} D(f) ) ).$$ Một cấu xạ giữa các lược đồ affine là một cấu xạ tại "từng vị trí" của biểu diễn như trên (tại điểm này, mình đã bỏ qua lý thuyết bó, các bạn có thể xem bài của anh nmlinh16 để tìm hiểu thêm - tuy nhiên điều đó không thật sự quan trọng ở đây). Một đồng cấu vành $\phi:R \longrightarrow R'$ cho ta một đồng cấu lược đồ affine

$$\mathrm{Spec}(R') \longrightarrow \mathrm{Spec}(R), \mathfrak{q} \longmapsto \phi^{-1}(\mathfrak{q}).$$ và xây dựng $R \longmapsto \mathrm{Spec}(R)$ bảo toàn thông tin:

 

Nghiên cứu một vành cũng bằng với nghiên cứu lược đồ affine của nó.

 

 

Giống như đa tạp là việc dán các mảnh $\mathbf{R}^n$, ở đây ta có:

 

Định nghĩa. Một lược đồ là một không gian tô-pô mà về mặt địa phương (tức là mỗi điểm có một lân cận) là một lược đồ affine.

 

Lại là điểm - nhưng hình học!

 

Ta biết rằng mỗi một điểm $\mathfrak{p} \in \mathrm{Spec}(R)$ cho ta một thông tin, đó là trường thặng dư $\kappa(\mathfrak{p}) = \mathrm{Frac}(R/\mathfrak{p})$. Đồng cấu vành $R \longrightarrow \mathrm{Frac}(R/\mathfrak{p})$ cho ta một đồng cấu lược đồ $\mathrm{Spec}(\kappa(\mathfrak{p})) \longrightarrow \mathrm{Spec}(R)$ như lưu ý ở phần trước.

 

Định nghĩa. Một điểm của lược đồ $\mathrm{Spec}(R)$ là một cấu xạ $\mathrm{Spec}(k) \longrightarrow \mathrm{Spec}(R)$ trong đó $k$ là một trường. Khi $k$ là đóng đại số, ta gọi nó là điểm hình học.

 

Giờ bạn có thể nghĩ rằng $\mathrm{Spec}(k)$ chỉ là một điểm (vì $k$ là một trường, nên chỉ có một ideal khác $(1)$ là $(0)$) thì có gì thú vị mà nghiên cứu?

 

Nghĩ vậy thì bạn nhầm! Về mặt tô-pô nó là một điểm, nhưng đừng quên nó mang trên mình "phép gán vành" (mỗi tập mở được gán một vành), do đó các hàm trên $\mathrm{Spec}(k)$ là cả $k$ nên nó có thể rất to.

 

Về mặt tô-pô thì $\mathrm{Spec}(k)$ là một điểm nên cấu xạ $\mathrm{Spec}(k) \longrightarrow \mathrm{Spec}(R)$ xác định cho ta một điểm $\mathfrak{p}$. Về mặt đồng cấu vành nó cho ta một dãy đồng cấu vành

$$R \longrightarrow \kappa(\mathfrak{p}) \longrightarrow k$$

và do đó ta có thể nói về giá trị hàm $f \in R$ như ảnh của dãy đồng cấu vành này. Tóm lại điểm vẫn là chỗ mà ta tính giá trị, và giá trị nằm trong một trường.

 

Thế thì tại sao lại quan tâm đến tính đóng đại số (điểm hình học)? Thực ra điểm hình học là chỗ ta tìm nghiệm đầu tiên. Hãy nhớ lại rằng việc giải phương trình

$$x^{7.000.000.000}-2=0$$

trên $\mathbf{Q}$ tương đương với việc tìm các cấu xạ (lát cắt) $\mathrm{Spec}(\mathbf{Q}) \longrightarrow \mathrm{Spec}(\mathbf{Q}[x]/(x^{7.10^9}-2))$. Tuy nhiên ta biết rằng phương trình này không có nghiệm trên $\mathbf{Q}$ đơn giản do $2$ thậm chí còn không có căn bậc $2$ do đó chẳng có cấu xạ nào như vậy. Nhưng nếu ta xem xét điểm hình học $\mathrm{Spec}(\mathbf{C}) \longrightarrow \mathrm{Spec}(\mathbf{Q}[x]/(x^{7.10^9}-2))$ thì tương đương với việc giải

$$x^{7.000.000.000}-2=0$$

trong $\mathbf{C}$, do đó nó có tới $7$ tỷ nghiệm, và do đó tương ứng với $7$ tỷ cấu xạ!

 

Quay lại với phương trình nghiệm nguyên

 

Như trong phần đầu tiên đã hứa rằng nói việc giải địa phương một hệ phương trình đa thức hệ số nguyên

$$f_1(x_1,...,x_n) = ... = f_r(x_1,...,x_n)=0 (f_i \in \mathbf{Z}[x_1,...,x_n])$$

tương đương với với việc giải địa phương quanh số nguyên tố $p$. Tức là giải quanh lân cận của ideal $(p) \in \mathrm{Spec}(\mathbf{Z})$. Tuy nhiên ta đã biết rằng các lân cận này rất xấu. Thực tế, chúng xấu vì cái tô-pô chúng xác định xấu. Tô-pô Zariski quá thô (đa số các tập mở đều to, đều trù mật). Làm thế nào để có một tô-pô mịn hơn tô-pô Zariski mà việc giao tất cả lân cận cho ta "một điểm" như trong trường hợp tô-pô?

 

Câu trả lời là một trong các phát kiến cực kỳ sáng tạo của Grothendieck và trường phái của ông: tô-pô étale (tô-pô étale làm cho định lý hàm ngược đúng). Nhưng ngay cả tô-pô étale cũng chưa phải tô-pô đúng trong trường hợp này. Mà nó là cái gọi là tô-pô Nisnevich. Tuy nhiên cả hai tô-pô này quá phức tạp để giới thiệu cho một người mới bắt đầu học hình học đại số do đó ta hãy phủi tay một chút.

 

Giả thiết. Tồn tại một tô-pô trên $\mathrm{Spec}(R)$ mà giao tất cả tập mở chứa $(p)$ cho ta một không gian mà các hàm trên không này là một vành ký hiệu $R_{\mathfrak{p}}^h$. Nó là một $R_{\mathfrak{p}}$-đại số và là một vành địa phương với ideal cực đại $\mathfrak{p}R_{\mathfrak{p}}^h$.

 

Bạn có thể đoán rằng $\mathbf{Z}_{(p)}^h$ là các số nguyên $p$-adic. Nếu vậy, bạn lại nhầm. Tuy nhiên ta biết rằng ta đã đến gần hơn với câu trả lời. Hãy để mình gọi $\mathbf{Z}_{(p)}^h$ là "Hensel hóa" của $\mathbf{Z}_{(p)}$. Tức là nó thỏa mãn bổ đề Hensel.

 

Định nghĩa. Cho $(A,\mathfrak{m},k)$ là một vành địa phương (tức là $\mathfrak{m}$ là ideal cực đại duy nhất, $k=A/\mathfrak{m}$ là trường thặng dư), với mỗi $f \in A[x]$, ta ký hiệu $\overline{f}$ là ảnh của $f$ qua phép lấy modulo $\mathfrak{m}$, $A[x] \longrightarrow k[x]$. Ta nói $A$ thỏa mãn bổ đề Hensel hay gọi $A$ là vành Hensel nếu $f \in A[x]$ có phân tích $\overline{f}=g_0h_0$ trong $k[x]$ thì tồn tại $g,h \in A[x]$ sao cho $f=gh$ và $\overline{g}=g_0$ và $\overline{h}=h_0$.

 

Nói cách khác, phân tích trong $k[x]$ có thể nâng lên thành phân tích trong $A[x]$. Nói riêng, nghiệm trong $k[x]$ có thể nâng lên thành nghiệm trong $A[x]$.

 

Để thực sự đạt được câu trả lời ta hãy quay lại với trường hợp hàm phức, nơi mà tô-pô đủ tốt để ta không phải thêm thắt gì và hãy đoán xem Hensel hóa của $\mathbf{C}[x]_{(x-a)}$ (các hàm với mẫu không có nghiệm $a$) là gì?

 

Phương pháp chuỗi giải phương trình vi phân. Làm thế nào để giải một phương trình vi phân một biến $Df=0$ tại lân cận một điểm? Phương pháp dễ nhất là phương pháp chuỗi, nó thực hiện theo hai bước sau.

• Tìm một nghiệm hình thức $\mathbf{C}[[x-p]]$ (các chuỗi hình thức, không có điều kiện hội tụ) bằng cách thế nào phương trình và kiểm tra xem các hệ số này cho ta cái gì.
• Kiểm tra xem chuỗi này hội tụ không. Ta ký hiệu $\mathbf{C}\left \langle x-p  \right \rangle$ là tập các chuỗi $\sum_{i=0}^{\infty}a_i(x-a)^i$ mà có bán kính hội tụ dương. Tập này dĩ nhiên là một vành.

Một lợi thế của việc tìm nghiệm trong $\mathbf{C}\left \langle x-a  \right \rangle$ là phương trình $Df=0$ có nghiệm khi và chỉ khi tồn tại các đa thức $f_n \in \mathbf{C}[x-a]$ với $\mathrm{deg}(f_n) \leq n$ sao cho $Df_n=0$ và dãy $(f_0,f_1,...f_n,...)$ hội tụ theo một nghĩa nào đó: các hệ số của nó cho ta một chuỗi có bán kính hội tụ dương. Như vậy bạn có thể đoán rằng $\mathbf{C}[x]_{(x-a)}^h = \mathbf{C}\left \langle x-a  \right \rangle$ tuy nhiên ta cần ghi nhớ tính chất đặc biệt bằng việc xấp xỉ đa thức của $\mathbf{C}\left \langle x-a  \right \rangle$

$$\mathbf{C}[x]_{(x-a)}^h = \mathbf{C}\left \langle x-a  \right \rangle = \lim \ \mathbf{C}[x]_{(x-a)}^h/ (x-a)^n.$$

Nói cách khác, ta nên xem xét vành

$$\lim \mathbf{Z}^h_{(p)}/p^n \mathbf{Z}^h_{(p)} = \mathbf{Z}_{(p)}/p^n\mathbf{Z}_{(p)} = \lim \mathbf{Z}/p^n\mathbf{Z}$$

Và vành này hóa ra lại là vành các số nguyên $p$-adic $\mathbf{Z}_p$ (chứ không phải $\mathbf{Z}_{(p)}^h$ như trường hợp trên) và tiêu chuẩn xấp xỉ bởi đa thức được viết lại thành cái mà chúng ta đã có ở bài trước.

 

Định lý. Một phương trình có nghiệm $p$-adic khi và chỉ khi nó có nghiệm modulo $p^n$ với mọi $n$.

 

Tóm lại ta vừa chứng minh rằng làm việc địa phương tức là giải $p$-adic một hệ phương trình $f_1=...=f_r$ thì tương đương với tìm các biểu đồ giao hoán

\begin{xy}
\xymatrix {
 \mathrm{Spec}(\mathbf{Z}_p)  \ar[r] \ar[dr]& \mathrm{Spec}(\mathbf{Z}_p[x_1,...,x_n]/(f_1,...,f_r)) \ar[d] \\
& \mathrm{Spec}(\mathbf{Z}_p)
}
\end{xy}

 

Ta sẽ ứng dụng nó để tìm hiểu (không phải chứng minh đủ) một định lý rất nổi tiếng trong số học, định lý Legendre nôm na nói rằng một phương trình thuần nhất bậc hai ba biến có nghiệm khi và chỉ khi nó có tất cả các nghiệm địa phương. Nhưng trước tiên ta hãy chứng minh một định lý thú vị hơn trong giải tích phức: định lý Liouville. Định lý Liouville nói rằng hàm chỉnh hình bị chặn trên toàn mặt phẳng thì là hằng số.

 

Trước tiên ta hãy đến với một lớp lược đồ cực kỳ quan trọng: các không gian xạ ảnh!

 

Không gian xạ ảnh: một lớp lược đồ không affine

 

Trong phần trước mình đã định nghĩa một lược đồ là hợp của các lược đồ affine nhưng thực tế chỉ làm việc với các lược đồ affine nên có thể bạn sẽ hỏi: có hay không các lược đồ không affine? Dĩ nhiên câu trả lời là có rất nhiều, nếu không người ta không cần tốn công vẽ ra lược đồ làm gì vì chỉ làm với affine thì cũng tương đương làm với vành. Tuy nhiên điều này không có nghĩa bạn có thể làm việc trực tiếp với các lược đồ mà bỏ qua phần affine. Giống như các tính toán trên đa tạp bạn luôn phải quy về các bản đồ địa phương thì ở đây cũng vậy.

 

Slogan. Làm địa phương, kết quả toàn cục.

 

Một lớp lược đồ rất quan trọng (mà hầu hết các lược đồ khác đều được nhúng vào chúng theo nghĩa nào đó) là các không gian xạ ảnh trên trường (ở đây ta bỏ qua các vành để tránh phiền phức). Để hiểu chúng ta hãy tới với ví dụ đơn giản nhất: đường thẳng xạ ảnh (projective line) hay còn gọi trong giải tích phức là mặt cầu Riemann.

 

Mặt cầu Riemann $S = \mathbf{P}^1 = \mathbf{C} \cup \left \{\infty \right \}$ là cách ta thêm vào mặt phẳng một điểm vô cùng, thường được biểu diễn bằng cách lấy trong không gian ba chiều (ba chiều thực, vì $\mathbf{C}$ là hai chiều phức) sau đó lấy điểm cực bắc $N = (0,0,1)$ chiếu xuống.

 

Nhưng như vậy thì tô-pô của $\mathbf{P}^1$ xung quanh $N=\infty$ là như thế nào (do nó không nằm trên $\mathbf{C}$ nên tô-pô của nó không hiển nhiên), bạn có thể thấy rằng một lân cận vô cùng bé của $N$ trên mặt cầu sẽ chiều một vùng vô cùng lớn xung quanh gốc tọa độ $\mathbf{0}=(0,0,0)$. Đây là cách định nghĩa dễ nhất. Về mặt đại số nó nói rằng tọa độ $z$ tiến về $N$ khi và chỉ khi hàm $\frac{1}{z}$ tiến về $0$. Nói cách khác,

$$\frac{1}{z}(\infty) = 0$$

và hơn nữa $\frac{1}{z}(\mathbf{0}) = \infty$. Nếu bây giờ bạn lắp một mặt phẳng song song với $\mathbf{C}$ với gốc tọa độ mới là $N$ thì bạn đã đảo vị trí của $N$ và $\mathbf{0}$ và điều này diễn tả dạng đại số là

$$z(\infty) = \infty, z(0) = 0.$$

Tất cả những điều mình vừa thảo luận để nói rằng nếu bạn chỉ dùng cả mặt cầu thì không đủ sức để tô-pô hóa $S$ mà bạn phải dùng hai mảnh $U=S \setminus \left \{\infty \right \}$ và $V=S \setminus \left \{\mathbf{0} \right \}$. Bạn lần lượt có hai hàm tọa độ: $\frac{1}{z}$ trên $V$ và $z$ trên $U$. Hai mảnh $U,V$ đẳng cấu với nhau qua phép đảo tọa độ  $z \mapsto \frac{1}{z}$. Thông qua phép đảo này hai điểm $0$ và $\infty$ đổi vị trí cho nhau. Nhớ rằng $U = \mathbf{C}$ là đường thẳng (đường thẳng vì nó một chiều phức - chứ không phải xét hai chiều thực tức là mặt phẳng) và do đó $V$ cũng là đường thẳng.

 

Điều này gợi ý một cách làm đại số: ta tìm hai đường thẳng và dán chúng lại ở phần giao. Vậy cái gì đóng vai tró một đường thẳng? Chúng ta vốn đã biết rồi, nó chính là $\mathrm{Spec}(\mathbf{C}[x])$ mà từ giờ sẽ ký hiệu hiệu là $\mathbf{A}_{\mathbf{C}}^1$. Các điểm của nó chỉ là các ideal $(x-a)$ và ứng với các điểm $a$ trong $\mathbf{C}$. Ta đã xử lý được mảnh $U$, còn mảnh $V$. Ta nhớ rằng $V$ là chỗ mà tọa độ $x$ khả nghịch. Vậy đơn giản nhất ta lấy mảnh $V$ là $\mathrm{Spec}(\mathbf{C}\big[\frac{1}{x} \big])$.

 

Định nghĩa. Đường thẳng xạ ảnh $\mathbf{P}^1$ là một lược đồ có một phủ mở gồm hai lược đồ $\mathrm{Spec}(\mathbf{C}[x]) \cup \mathrm{Spec}(\mathbf{C}\big[\frac{1}{x} \big])$ và trên phần giao $\mathbf{C}\big[x,\frac{1}{x}\big]$ chúng được tính thông qua phép nghịch đảo tọa độ $x \mapsto \frac{1}{x}$.

 

Một hàm trên $\mathbf{P}^1$ thì trông như thế nào? Trước tiên một hàm trên $\mathbf{P}^1$ thì phải là hàm trên cả hai mảnh $U,V$ và bằng nhau trên phần giao $U \cap V$. Một hàm trên $U$ thì là một đa thức $f(x)$ còn một hàm trên $V$ là một đa thức $g(\frac{1}{x})$ và chúng bằng nhau khi và chỉ khi chúng là hằng số trên $\mathbf{C}$. Đây chính là nội dung của định lý Liouville đại số. Ta còn suy ra một hệ quả quan trọng nữa: $\mathbf{P}^1$ không affine, vì nếu affine thì nó phải đẳng cấu với phổ $\mathrm{Spec}(\mathbf{C})$ của tất cả các hàm của nó, nhưng phổ này là phổ của một trường nên tầm thường trong khi $\mathbf{P}^1$ có rất nhiều điểm.

 

Làm thế nào để mở rộng xây dựng này lên trường hợp nhiều chiều?

 

Điều này không quá khó nếu ta nhìn vào các điểm của $\mathbf{P}^1$ (trong trường hợp giải tích). Chúng tham số hóa cái gì? Rõ ràng một điểm trên mặt phẳng $\mathbf{C}$ nối với điểm cực bắc $N$ cho ta một đường thẳng, nó cắt mặt cầu tại duy nhất một điểm. Nói cách khác, mỗi điểm khác $N$ tương ứng với duy nhất một đường thẳng. Nhưng bản thân $N$ có thể xem là một đường thẳng suy biến. Nói cách khác, $\mathbf{P}^1$ có điểm là các đường thẳng.

 

Điều này cho ta một mô tả khác của $\mathbf{P}^1$: mỗi điểm của nó là một bộ $(x_0,x_1)$ với $x_i \in \mathbf{C}$ nhưng chỉ xác định chính xác phép nhân với vô hướng khác không, i.e. $(x_0,x_1) = (\lambda x_0, \lambda x_1)$ với $\lambda \in \mathbf{C}^{\times}$ (do mỗi đường thẳng qua gốc tọa độ chỉ xác định duy nhất bằng một điểm và các điểm còn lại là bội của điểm này). Khi đó mảnh $U$ và $V$ lần lượt tương ứng với vị trí $x_0 \neq 0$ và $x_1 \neq 0$, do đó các điểm trong $U,V$ lần lượt có dạng $\big[1,\frac{x_1}{x_0}]$ và $\big[\frac{x_0}{x_1},1\big]$ và nếu dùng cách này ta có thể viết

$$\mathbf{P}^1 = \mathrm{Spec}(\mathbf{C}\big[\frac{x_0}{x_1}\big]) \cup \mathrm{Spec}(\mathbf{C}\big[\frac{x_1}{x_0}\big]),$$

và giờ hãy tự thuyết phục bạn rằng nếu $\mathbf{P}^n$ tham số hóa các đường thẳng trong không gian $n$-chiều thì nó phải cái gì đó trông như thế này

$$\mathbf{P}^n = \bigcup_{i=0}^n \mathrm{Spec}\bigg(\mathbf{C}\big[\frac{x_0}{x_i},...,\frac{x_{i-1}}{x_i},\frac{x_{i+1}}{x_i},...,\frac{x_n}{x_i} \big]\bigg).$$

và các phép chuyển tọa độ giữa hai mảnh

$$\mathrm{Spec}\bigg(\mathbf{C}\big[\frac{x_0}{x_i},...,\frac{x_{i-1}}{x_i},\frac{x_{i+1}}{x_i},...,\frac{x_n}{x_i} \big]\bigg) \longrightarrow \mathrm{Spec}\bigg(\mathbf{C}\big[\frac{x_0}{x_j},...,\frac{x_{j-1}}{x_j},\frac{x_{j+1}}{x_j},...,\frac{x_n}{x_j} \big]\bigg)$$

sẽ là $\frac{x_k}{x_i} \mapsto \frac{x_k}{x_i} \frac{x_i}{x_j}$. Tương tự với $\mathbf{P}^1$, bạn có thể chứng minh tất cả các hàm trên $\mathbf{P}^n$ là hàm hằng.

 

Vậy bạn sẽ hỏi nếu lược đồ affine cho ta một cách nhìn về việc giải phương trình thì $\mathbf{P}^n$ có cho ta cách nhìn nào như vậy không? Và nếu có các phương trình của nó có dạng nào không?

 

Câu trả lời là nó giúp ta giải các phương trình thuần nhất. Một đa thức thuần nhất bậc $d$ là một đa thức $f(x_1,...,x_n)$ thỏa mãn

$$\lambda^d f(x_1,...,x_n) = f(\lambda x_1,...,\lambda x_n)$$

do đó bộ nghiệm của $f(x_1,...,x_n)=0$ xác định trên từng đường thẳng, ví dụ $x_0^2+x_1^2-x_2^2=0$, và sẽ hợp lý hơn nếu ta lấy nghiệm trong không gian xạ ảnh. Với mọi đa thức thuần nhất $f$ như vậy ta có thể xây dựng một không gian tương tự như không gian xạ ảnh mà sẽ ký hiệu là $\mathrm{Proj}\bigg(\frac{\mathbf{C}[x_1,...,x_n]}{f(x_1,...,x_n)}\bigg)$ (ở đây $\mathbf{P}^n = \mathrm{Proj}(\mathbf{C}[x_1,...,x_n])$). Để làm như vậy ta xây dựng trên từng mảnh $\mathrm{Spec}\bigg(\mathbf{C}\big[\frac{x_0}{x_i},...,\frac{x_{i-1}}{x_i},\frac{x_{i+1}}{x_i},...,\frac{x_n}{x_i} \big]\bigg)$ và dán chúng lại với nhau. Ví dụ với phương trình $x_0^2+x_1^2=x_2^2=0$ thì trên mảnh mà $x_2 \neq 0$ thì nó tương đương với việc tìm các lát cắt của

$$\mathrm{Spec}(\mathbf{C}[t_0,t_1]/(t_0^2+t_1^2-1)) \longrightarrow \mathrm{Spec}(\mathbf{C})$$

(lưu ý ở đây ta có thể thay $\mathbf{C}$ bằng $\mathbf{Z}$ hay $\mathbf{Q}$ tùy ý) và tương tự ở chỗ $x_0,x_1\neq0$. Ta giải rồi dán chúng lại với nhau để nhận được nghiệm toàn cục.

 

Định lý Legendre

 

Giờ ta hãy xem xét cách giải địa phương định lý Legendre (không phải chứng minh hoàn chỉnh) thì như thế nào.

 

Định lý Legendre. Cho $a,b,c \in \mathbf{Z}$ là ba số nguyên khác không và đôi một nguyên tố cùng nhau. Khi đó phương trình

$$f_{a,b,c}(x,y,z) = ax^2+by^2+cz^2$$

có nghiệm khi và chỉ khi hai kiện sau cùng thỏa mãn:

• Ba số $a,b,c$ không cùng dấu.
• $-ab$ là bình phương modulo $\left|c\right|$, $-bc$ là bình phương modulo $\left|a \right|$, $-ac$ là bình phương modulo $\left|b \right|$.

Chứng minh. Ta đã nói rằng việc giải phương trình $f_{a,b,c}(x,y,z)$ thì tương đương với việc tìm các biểu đồ

\begin{xy}
\xymatrix {
 \mathrm{Spec}(\mathbf{Z})  \ar[r] \ar[dr]& \mathrm{Proj}\bigg(\frac{\mathbf{Z}[x,y,z]}{f_{a,b,c}(x,y,z)}\bigg) \ar[d] \\
& \mathrm{Spec}(\mathbf{Z})
}
\end{xy}

và do đó tìm nghiệm $p$-adic, hay còn gọi là nghiệm địa phương thì tương đương với việc "giải biểu đồ"

\begin{xy}
\xymatrix {
 \mathrm{Spec}(\mathbf{Z}_p)  \ar[r] \ar[dr]& \mathrm{Proj}\bigg(\frac{\mathbf{Z}_p[x,y,z]}{f_{a,b,c}(x,y,z)}\bigg) \ar[d] \\
& \mathrm{Spec}(\mathbf{Z}_p)
}
\end{xy}

(sẽ không vấn đề nếu ta thay $\mathbf{Z}_p$ bằng $\mathbf{Q}_p$) rồi ta sẽ hy vọng với mọi $p$ tồn tại một nghiệm địa phương thì sẽ tồn tại một nghiệm hữu tỷ (do đó nghiệm nguyên). Vậy làm thế nào tìm nghiệm địa phương? Ta dựa vào bổ đề Hensel, nó nói nôm na rằng nếu phương trình có nghiệm trên $\mathbf{Z}/p$ thì sẽ có nghiệm trên $\mathbf{Z}_p$. Giờ hãy xem xét phương trình

$$f_{a,b,c}(x,y,z) = ax^2+by^2+cz^2 = 0 \ \mathrm{mod} \ p$$

Có hai trường hợp:

• Nếu $p$ không là ước của cả ba số $a,b,c$ thì ta có thể giả sử $c=1$ và do đó quy về giải $ax^2+by^2+z^2=0$ và do đó rút gọn về phương trình $ax^2+by^2+1=0$. Nói cách khác hai tập $\left \{ax^2 \right \}$ và $\left \{-by^2-1\right \}$ phải có phần giao. Do $a,b$ khác $0$ modulo $p$ nên mỗi tập này có chính $\frac{p-1}{2}+1$ phần tử, hợp của cả hai tập do đó có $p+1$ phần tử, nhiều hơn $1$ so với số phần tử của $\mathbf{Z}/p$. Do đó chúng có phần giao, là nghiệm. Theo bổ đề Hensel thì $f_{a,b,c}$ có nghiệm trong $\mathbf{Q}_p$.
• Nếu $p$ là ước của một trong ba số $a,b,c$ thì nó chỉ là ước của duy nhất một trong ba số $a,b,c$. Không giảm tổng quát ta giả sử $p \mid c$. Ta tìm nghiệm địa phương ở bản đồ $\mathrm{Proj}\bigg(\frac{\mathbf{Z}[x,y,z]}{f_{a,b,c}(x,y,z)}\bigg) \cap \mathrm{Spec}(\mathbf{Z}\big[\frac{x}{z},\frac{y}{z}\big])$ tức là chỗ mà $z \neq 0$. Ở bản đồ này $f_{a,b,c}$ trơn (như vậy mới áp dụng được bổ đề Hensel) trên $\mathbf{Z}_p$. Như vậy một lần nữa ta quy về việc giải $ax^2+by^2=0$ trên $\mathbf{Z}/p$ với điều kiện $z \neq 0$. Theo giả thiết thì $-ab$ là bình phương modulo $p$ nên $-ab = t^2$ và phương trình ban đầu có thể viết lại $(ax)^2 = (ty)^2$. Ta thử giải $ax=ty$. Do $t \neq 0$ (vì $p$ không là ước của $ab$) nên nó tương đương với $(at^{-1})x=y$, phương trình này có nghiệm $x=1,y=at^{-1}$.

Như vậy ta đã hoàn tất bài toán giải địa phương. Vậy để kết luận nó có thể nâng lên một nghiệm toàn cục là nội dung của nguyên lý địa phương-toàn cục (hay còn gọi là nguyên lý Hasse) mà anh @nmlinh16 đã bàn tới trong bài này.