Dấu $=$ của bạn sai rồi, $x+y+z=3$ cơ mà

Nhầm, đã fix

có cách thcs hk 

Bạn đọc không hiểu à? Đây chỉ là kiến thức biến đổi nhẹ thôi, chưa đụng cao đâu, lớp 8 làm bình thường mà,

Phương trình đã cho là dạng $ax+b=0$, chỉ có khả năng có một nghiệm, vô nghiệm hay vô số nghiệm thôi.

Cho mình đóng góp cùng nha:
Bài 1***: Cho phương trình: m-2x+m-3=0(với m là tham số).Tìm các giá trị của "m'' để phương trình có 2 nghiệm  $x_{1}x_{2}$ thỏa mãn điều kiện: $x_{1}^{3}.x2+x^{_{1}}.x_{2}^{3}=-6$

 

Chắc đề cho pt này : $mx^2-2x+m-3=0$

Ang trừ em 2 lỗi nhé : 

1) Sử dụng sai định lý (1đ) 

2) Gõ $Latex$ sai (1đ ) 

 

 

Anh ơi latex em có sai đâu? Anh tô màu đỏ 1 đoạn trong công thức dãy latex em viết nên cả đoạn biến đổi đấy không hiển thị được chứ không phải em gõ sai mà

Cho $x,y\in \mathbb{R}$ thỏa mãn $(x+y)^{3}+4xy\geq 2$(*) . Tìm giá trị nhỏ nhất của:

 

$$ P=3(x^{4}+y^{4}+x^{2}y^{2})-2(x^{2}+y^{2})+1$$

Đề của 

nk0kckungtjnh

Bài làm:

P=3x⁴+3y⁴+3x²y²-2x²-2y²+$\frac{1}{3}$.3

P=3(x⁴-$\frac{2}{3}$x²+$\frac{1}{9}$)+3(y⁴-$\frac{2}{3}$y²+$\frac{1}{9}$)+3x²y²+$\frac{1}{3}$

P=3(x²-$\frac{1}{3}$)²+3(y²-$\frac{1}{3}$))²+3x²y²+$\frac{1}{3}$

Nhận thấy:3(x²-$\frac{1}{3}$)²+3(y²-$\frac{1}{3}$))²$\geq 0$

                 3x²y²$\geq 0$

Vậy nên để P có min thì cặp số x,y phải thoả mãn 1 trong hai điều kiện sau:3(x²-$\frac{1}{3}$)²+3(y²-$\frac{1}{3}$))²=0

                                                                                                                       3x²y²=0

 

*Trường hợp 1:3x²y²=0

Theo bài toán đầu đề thì ta nhận thấy x,y không thể cùng bằng 0

Mà theo trường hợp thì x=0 hoặc y=0

Giả sử x=0 và y=m,thay x=0 vào bài toán đầu bài(*) ta có được y$\geq$$\sqrt[3]{2}$

Thay x=0,y$\geq$$\sqrt[3]{2}$ vào P ta có=3(0-$\frac{1}{3}$)²+3(y²-$\frac{1}{3}$)²+0+$\frac{1}{3}$$\geq$5,4(1)

*Trường hợp 2 :3(x²-$\frac{1}{3}$)²+3(y²-$\frac{1}{3}$))²=0

=>x=$\sqrt{\frac{1}{3}}$ hoặc x=$-\sqrt{\frac{1}{3}}$và y=$-\sqrt{\frac{1}{3}}$ hoặc y=$\sqrt{\frac{1}{3}}$

vậy nên ta sẽ có được 4 cặp số thoả mãn trường hợp

Thay lần lượt 4 cặp số vừa tìm được vào bài toán đầu bài(*) thì ta chỉ nhận được 1 cặp số x,y thoả mãn là:

(x,y)=($\sqrt{\frac{1}{3}}$;$\sqrt{\frac{1}{3}}$)

Thay cặp x,y ở trên vào P ta có P$\geq \frac{2}{3}$(2)

Từ (1),(2) suy ra P$\geq \frac{2}{3}$ cho nên Min của P là $\frac{2}{3}$. dấu bằng xảy ra khi x=y=$\sqrt{\frac{1}{3}}$

Bài làm đã sai ngay từ bước lập luận màu đậm kia, vì vậy các bước giải sau cũng sai và kết quả sai.

Cho $x,y\in \mathbb{R}$ thỏa mãn $(x+y)^{3}+4xy\geq 2$ . Tìm giá trị nhỏ nhất của:

$$ P=3(x^{4}+y^{4}+x^{2}y^{2})-2(x^{2}+y^{2})+1$$

Đề của 

nk0kckungtjnh

MSS54:

Áp dụng BĐT Cauchy cho 2 số không âm $x^2;y^2$ thì $x^2+y^2 \geq 2.\sqrt{x^2y^2}=2|xy|$ (1)

$\Rightarrow (x+y)^2 \geq 4xy \Rightarrow (x+y)^3+(x+y)^2 \geq (x+y)^3+4xy \geq 2$

$\Rightarrow (x+y)^3+(x+y)^2-2 \geq 0 \Rightarrow (x+y-1)[(x+y)^2+2(x+y)+2] \geq 0$

Mà $(x+y)^2+2(x+y)+2=(x+y+1)^2+1 \geq 1>0$ nên có $x+y-1 \geq 0 \Rightarrow x+y \geq 1$

Cũng từ (1) ta có $x^2+y^2 \geq \frac{(x+y)^2}{2} \geq \frac{1}{2}$ (2) và $(x^2+y^2)^2 \geq 4x^2y^2 $ (3)

Ta biến đổi P và áp dụng các BĐT (2) và (3) ta có:

$P=3(x^4+y^4+x^2y^2)-2(x^2+y^2)+1 \\ =3[(x^2+y^2)^2-2.x^2y^2+x^2y^2]-2(x^2+y^2)+1 \\ =3[(x^2+y^2)^2-x^2y^2]-2(x^2+y^2)+1 \\ \geq 3 \Big[ (x^2+y^2)^2-\frac{(x^2+y^2)^2}{4} \Big] -2(x^2+y^2)+1 \\ =\frac{9}{4}.(x^2+y^2)^2-2(x^2+y^2)+1 \\ = \Big\{ \Big[ \frac{3}{2}.(x^2+y^2) \Big] ^2-2.\frac{3}{2}(x^2+y^2).\frac{3}{4} + \frac{9}{16} \Big\} + \Big[ \frac{1}{4}(x^2+y^2)+\frac{7}{16} \Big] \\ = \Big[ \frac{3}{2}.(x^2+y^2).\frac{3}{4} \Big] ^2+ \Big[ \frac{1}{4}(x^2+y^2)+\frac{7}{16} \Big] \\ \geq 0+ \Big( \frac{1}{4}.\frac{1}{2}+\frac{7}{16} \Big) \\ =\frac{9}{16}$ (Sai )

Tức ta có $P \geq \frac{9}{16}$

Dấu = xảy ra khi $\left\{\begin{matrix} x^2=y^2 & \\ (x+y)^3+4xy=2 & \\ x+y=1 & \\ \end{matrix}\right. \Leftrightarrow x=y=\frac{1}{2}$

Vậy Max $P=\frac{9}{16}$ khi $x=y=\frac{1}{2}$

Điểm 9.

 Một số bài khác có sai cả phần sử dụng BĐT AM - GM nhưng chỉ bị trừ 1 điểm thôi, bài của em chỉ đánh sai dấu - thành dấu . (lỗi đánh máy) mà trừ mất 2 điểm. Bài làm của em sao bị trừ nặng thế ạ?

Không khuyến khích lắm việc toán thủ lấy đề có sẵn trên mạng, có chăng thì cũng nên xào nấu lại xíu chứ lấy y nguyên lại thì không hay cho lắm thì phải

http://www.artofprob...11827d#p3103094

Tuy không khuyến khích thật nhưng mấy ai đã tìm đc đề này, dịch công phu và trả lời hoàn thiện như thế này đâu!

Ta có: ${(n^2+1)^2}^k . (44n^3 +11n^2+10n+2)=N^m $ (1).

Do các số n, k, m, N đều nguyên và không âm nên từ (1) ta có m, N luôn khác 0.

Ta xét các trường hợp:

- Xét n chẵn:

Ta có ${(n^2+1)^2}^k$ chia 4 dư 1và $(44n^3 +11n^2+10n+2)$ chia 4 dư 2 nên $N^m$ chia 4 dư 2.

Điều này xảy ra khi N=2 và m=1.

- Xét n lẻ suy ra $n=2a+1$ (với a không âm), ta có ${(n^2+1)^2}^k={2^2}^k . {[2a(a+1)+1]^2}^k$ . $(44n^3 +11n^2+10n+2)$ là số lẻ và chia 4 dư 3. (nói rõ hơn!!)

$\Rightarrow$ ${2^2}^k . {[2a(a+1)+1]^2}^k . (44n^3 +11n^2+10n+2)=N^m $

Để (1) xảy ra thì m lẻ, nên $N^m$ chẵn và N chẵn. (nói rõ hơn tại sao $m$ phải lẻ)

Khi đó từ (1) $\Rightarrow$ $N^m=(a.2^b)^m= a^m . 2^{b m}.$ (với a,b là các số nguyên dương; a là số lẻ)

$\Rightarrow {2^2}^k . {[2a(a+1)+1]^2}^k .(44n^3 +11n^2+10n+2)= a^m . 2^{bm}.$

Để tồn tại các số thỏa mãn đề thì ${2^2}^k=2^{bm}.$

$\Rightarrow 2^k= bm.$

Do các số đều nguyên nên để điều này xảy ra thì điều kiện cần là m =1 (do m là số lẻ)

$\Rightarrow$ đpcm.

Điểm. 9

S = 9.7+9*3 = 36.7

Giải phương trình: $2x^{2}+5x-1=7\sqrt{x^{3}-1} (1)$

Đề thi của l4lzTeoz

MSS54:

ĐKXĐ: $\forall x \in \mathbb{R}; x \geq 1$

Ta có pt: $(1) \Leftrightarrow 3(x-1)+2(x^2+x+1)=7\sqrt{(x - 1)(x^2+ x + 1)}$

- Xét x = 1 thì (1) trở thành: $2.1^2+5.1-1=7\sqrt{1^3-1} \\ \Leftrightarrow 6=0$

Điều này vô lí $\Rightarrow$ x = 1 không là nghiệm của (1).

- Xét $x \neq 1$ thì (1) $\Leftrightarrow 3+\dfrac{2(x^2+x+1)}{x-1}= 7\sqrt{\dfrac{x^2+x+1}{x-1}} (2)$

Đặt $\sqrt{\dfrac{x^2+x+1}{x-1}}=t (t \geq 0)$ thì (2) trở thành: $3+2t^2=7t \\ \Leftrightarrow 2t^2-6t-t+3=0 \\ \Leftrightarrow (t-3)(2t-1)=0 \\ \Leftrightarrow \begin{bmatrix}t=3 & \\ t=\dfrac{1}{2} & \end{bmatrix}$

(thỏa mãn đk: $t \geq 0$)

$\bigstar t=3$ $\Leftrightarrow \sqrt{\dfrac{x^2+x+1}{x-1}}=3 \Leftrightarrow \dfrac{x^2+x+1}{x-1}=9 \\ \Leftrightarrow x^2-8x+10=0(3)$

(3) là pt bậc hai ẩn x có $\Delta '=(-4)^2-1.10=6>0$ nên (3) có 2 nghiệm phân biệt: 

$\begin{bmatrix} x_1=\dfrac{-(-4)-\sqrt{6}}{1}=4-\sqrt{6} & \\ x_2=\dfrac{-(-4)+\sqrt{6}}{1}=4+\sqrt{6} & \end{bmatrix}$

(thỏa mãn ĐKXĐ và $x \neq 1$)

$\bigstar t=\dfrac{1}{2}$ $\Leftrightarrow \sqrt{\dfrac{x^2+x+1}{x-1}}=\dfrac{1}{2} \Leftrightarrow \dfrac{x^2+x+1}{x-1}=\dfrac{1}{4} \\ \Leftrightarrow x^2+\dfrac{3}{4}x+\dfrac{5}{4}=0(4)$

(4) là pt bậc hai ẩn x có $\Delta=(\dfrac{3}{4})^2-4.1.\dfrac{5}{4}=\dfrac{-71}{16}<0$ nên (4) vô nghiệm.

Như vậy pt (1) có tập nghiệm $S=\left \{4 \pm \sqrt{6} \right \}$

   d =10

   S =47

Đã sơ chấm xong trận này Chắc có sót đấy nên các em kiểm tra kĩ lại dùm nhé.
Nói chung cách làm với mở rộng na ná nhau cả nên điểm cộng thêm cho nhiều cách giải với mở rộng tối đa là 10 với 20 thôi nha
 

Thật sự anh cũng muốn như thế lắm em ạ :'(
Nhưng e phải hiểu là chấm bài trên máy tính rất chối, e phải lội từng page để xem bạn này có mở rộng hay có cách giải gì không, mà mỗi bài dài dằng dặc thì lăn lên lăn xuống rất khó chịu...
Chưa kể máy cùi bắp mở nhiều tab để chuyển qua lại cũng ngốn RAM + lag lắm.
Và điều quan trọng nhất.... đó là LƯỜI
Xin lỗi vì anh nói có phần vô trách nhiệm nhưng em hiểu đội ngũ trọng tài MSS vẫn còn là học sinh (có lúc thầy Thế chấm), vẫn còn ham ăn chơi nhảy múa lắm em ạ....
Nói chung "kể khổ" vậy thôi nhưng anh/em/mình sẽ tiếp thu, cố gắng hoàn thành công việc  .
(Nói nghe hơi chợ búa tí nhưng thế cho các em dễ hiểu tâm trạng )
 
Bonus:

Spoiler

Điểm của em ở đâu vậy anh

Trận BĐT lần trước cũng được dùng, k cần c/m.

P/S: MSS sắp kết thúc rồi, chỉ còn trận 10 nữa thôi. Em mong sau trận 9 này BTC sẽ lock các trận lại, chấm và thống kê tất cả lại theo từng trận và thông báo luôn toán thủ nào bị loại ở mỗi trận (giồng hai trận đầu tiên đấy ạ ) Thá mất thời gian chấm lâu chứ dây dưa điểm loại chưa rõ ràng đến trận 10 em thấy rất khó theo dõi.

Bạn với Hiếu có nhầm không nhỉ !?

Bởi tam giác $ABK$ vuông tại $K$ có góc $\angle ABK=60^o$ nên : $BK=\frac{AK}{tan(60^o)}=\frac{x}{\sqrt{3}}$ mới đúng chứ nhỉ !?

Hai thím kia tính sai rồi :v

chung : 9 , chuyên : 5 , đoán thế 

chuyên 9,5 chứ :3

thì bảo 35 trở lên không tèo

không đến độ 35 sp đâu, chỉ tầm 30 thôi 

tất nhiên là phải chứng minh rồi.

Mình không thi...nếu thi chắc làm được

HN k cần chứng minh đâu thím

35

25 là em tèo rồi chứ nói gì 35

Do đề của các Toán thủ nộp chưa phù hợp nên trận này BTC sẽ ra đề

Đề của BTC:
Cho tam giác $ABC$ nhọn. $D,E,F$ trên $BC, CA, AB$ sao cho $\triangle DEF$ nhọn và $AD, BE, CF$ đồng quy. $M, N, P$ trên $EF, FD, DE$ sao cho $\triangle MNP$ nhọn và $DM, EN, FP$ đồng quy.

Chứng minh rằng: $AM, BN, CP$ cũng đồng quy.

Thời gian làm bài tính từ: 20h15 ngày 14/2/2014

P/s: mong các toán thủ đừng mải đi chơi với gấu mà quên làm bài :adore:

Bài làm của MSS54:

Đầu tiên ta c/m định lí hàm số sin:

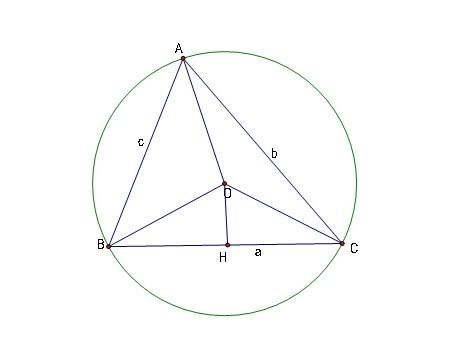
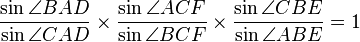Ngoài ra định lí Xê-va còn được phát biểu một cách tương đương trong lượng giác rằng:AD, BE, CF đồng quy   khi và chỉ khi  . (2)

MSS54:

Mở rộng: Đối với bài toán này không cần điều kiện các tam giác ABC, DEF và MNP nhọn:

" Cho tam giác ABC. D, E, F trên BC, CA, AB sao cho AD, BE, CF đồng quy. M, N, P trên EF, FD, DE sao cho DM, EN, FP đồng quy. Chứng minh AM, BN, CP cũng đồng quy."

Capture1.PNG

Ta có:

 

$\frac{S_{AME}}{S_{AMF}}= \frac{ME}{MF}$ (do $Sin \widehat{AMF}=Sin \widehat{AME}$)

 

$\frac{S_{AME}}{S_{AMF}}= \frac{AM\cdot AE\cdot Sin \widehat{MAE}}{AF\cdot AM\cdot Sin \widehat{MAF}}= \frac{ME}{MF}$

 

$\Rightarrow \frac{Sin \widehat{MAE}}{Sin \widehat{MAF}}= \frac{ME}{MF}\cdot \frac{AF}{AE} \left ( 1 \right )$

 

Tương tự:

 

$\frac{Sin \widehat{FBN}}{Sin \widehat{DBN}}= \frac{FN}{DN}\cdot \frac{BD}{BF}\left ( 2 \right )$

 

$\frac{Sin \widehat{PCD}}{Sin \widehat{PCE}}= \frac{PD}{PE}\cdot \frac{CD}{CE} \left ( 3 \right )$

 

Nhân cả hai vế của (1), (2), (3) với nhau, ta được:

 

$\frac{Sin \widehat{MAE}}{Sin \widehat{MAF}}\cdot \frac{Sin \widehat{FBN}}{Sin \widehat{DBN}}\cdot \frac{Sin \widehat{PCD}}{Sin \widehat{PCE}}= \frac{ME\cdot AF\cdot FN\cdot BD\cdot PD\cdot CD}{MF\cdot AE\cdot DN\cdot BF\cdot PE\cdot CE}$

 

hay $\frac{Sin \widehat{MAE}}{Sin \widehat{MAF}}\cdot \frac{Sin \widehat{FBN}}{Sin \widehat{DBN}}\cdot \frac{Sin \widehat{PCD}}{Sin \widehat{PCE}}= \left ( \frac{AF}{BF}\cdot \frac{BD}{CD}\cdot \frac{CE}{AE} \right )\cdot \left ( \frac{EM}{MF}\cdot \frac{FN}{ND}\cdot \frac{DP}{PE} \right )$

 

Vì AD, BE, CF đồng quy, DM, EN, FP đồng quy, theo định lí Ceva ta có:

 

$\frac{AF}{BF}\cdot \frac{BD}{CD}\cdot \frac{CE}{AE}= 1$

 

$\frac{EM}{MF}\cdot \frac{FN}{ND}\cdot \frac{DP}{PE}= 1$

 

$\Rightarrow \frac{Sin \widehat{MAE}}{Sin \widehat{MAF}}\cdot \frac{Sin \widehat{FBN}}{Sin \widehat{DBN}}\cdot \frac{Sin \widehat{PCD}}{Sin \widehat{PCE}}= 1$

 

Do $ \frac{Sin \widehat{MAE}}{Sin \widehat{MAF}}\cdot \frac{Sin \widehat{FBN}}{Sin \widehat{DBN}}\cdot \frac{Sin \widehat{PCD}}{Sin \widehat{PCE}}= 1$, theo Ceva-sin ta có AM, BN, CP đồng quy (đpcm)

Bài làm chỗ màu đỏ sai, hai góc kề bù làm sao có $\sin$ bằng nhau được, chỗ đó chỉ cần nói hai tam giác AMF và AME cùng chiều cao hạ từ A xuống EF nên thiết lập được tỉ số diện tích hai tam giác theo tỉ số hai cạnh đáy tương ứng. 

  Bài em vẫn chưa có điểm ạ.

MSS54: (làm tiếp)

Bảng giá trị thứ hai: 

Kết hợp cả 2 bảng giá trị ta thấy cặp số nguyên (x; y) thỏa mãn đề là (1; 2)

Tồn tại hay không các cặp số nguyên (x,y) thỏa mãn phương trình sau đây ?

$$\sqrt{2025x^2+2012x+3188}=2013x-2011y+2094(*)$$ 

Đề của 

lenin1999

MSS54:

Giả sử tồn tại cặp số (x; y) nguyên thỏa mãn (*)

Do x;y nguyên nên $2025x^2+2012x+3188$ và $2013x-2011y+2094$ cũng nguyên.

Kết hợp (*) $\Rightarrow 2025x^2+2012x+3188=m^2 (m \in Z)$

$\Rightarrow \sqrt{2025x^2+2012x+3188}=2013x-2011y+2094=|m|$

Hay $2013x-2011y=|m|-2094$(**)

Ta có $m^2-[(45x)^2+2012x+3188]=0 \\ \Leftrightarrow (45m)^2-[(45^2x)^2+45^2x.2012+3188.45^2]=0 \\ \Leftrightarrow (45m)^2- \Big[ [(45^2x)^2+2.45^2x.1006+1006^2]+5443664 \Big]=0 \\ \Leftrightarrow (45m)^2-(45^2x+1006)^2=5443664 \\ \Leftrightarrow [45m-(45^2x+1006)] . [45m+(45^2x+1006)]=5443664 (1)$

Do x; m nguyên nên $[45m-(45^2x+1006)]$ và $[45m+(45^2x+1006)]$ nguyên. (2)

Mà 5443664 $\vdots 2$ nên $[45m-(45^2x+1006)] . [45m+(45^2x+1006)] \vdots 2$

Xét tổng: $[45m-(45^2x+1006)]+[45m+(45^2x+1006)]=90m \vdots 2$ nên ta suy ra $[45m-(45^2x+1006)]$ và $[45m+(45^2x+1006)]$ đều $\vdots 2$ (3)

Kết hợp (**); (1); (2); (3) ta có bảng giá trị sau: