$\boxed{\text{Lời giải bài 29}}$
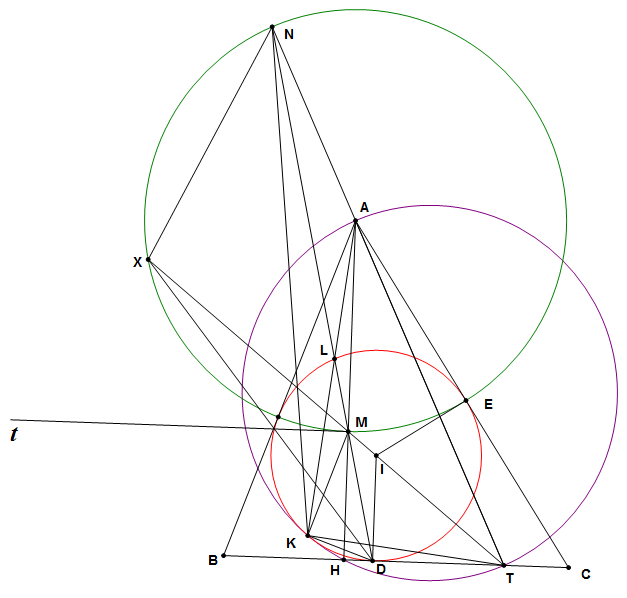
Gọi $T$ là giao điểm tiếp tuyến tại $B$, $C$ của $(O)$ và $L$ là điểm Lemoine của $\triangle ABC$. Ta có $(ADLT)=-1$ và $O, A', T$ thẳng hàng. Ta có $\widehat{BA'T}=\widehat{BEC}$ và $\widehat{BOA'}=\widehat{BAE}$ nên $\triangle BAE \sim \triangle BOA'$. Do đó $\frac{OA'}{OT}=\frac{OA'}{OB}.\frac{OB}{OT}=\frac{AE}{AB}.\cos{BAC}$. Đặt $BC=a, CA=b, AB=c$. Ta tính được $\frac{DB}{DC}=\frac{c^2}{b^2}$, suy ra $\frac{AE}{AC}=\frac{BD}{BC}=\frac{c^2}{c^2+b^2}$. Do đó $\frac{OA'}{OT}=\frac{bc}{b^2+c^2}.\frac{b^2+c^2-a^2}{2bc}=\frac{b^2+c^2-a^2}{2(b^2+c^2)}$. Mặt khác $(ADLT)=-1$, dùng đại số ta suy ra $(DTLA)=0,5$ do đó $\frac{LD}{LT}=\frac{AD}{2AT}$. Không khó để tính được tỉ số $\frac{AD}{AT}=\frac{b^2+c^2-a^2}{b^2+c^2}$. Do đó $\frac{LD}{LT}=\frac{OA'}{OT}$ hay $OL \parallel A'D$. Do $(ADLT)=-1$ nên $AA'$ chia đôi $OL$. Tương tự ta có đpcm.
P/s: bạn nào đề xuất bài mới giùm mình.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 5\\ \hline IHateMath & 1\\ \hline fatcat12345 & 4\\ \hline dogsteven & 5\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 2\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 2\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài 32}}$

Theo giả thiết, hai điểm $P, Q$ thỏa mãn tính chất trên được gọi là Antigonal conjugate. Ta có một tính chất rất đặc biệt của hai điểm liên hợp trên là liên hợp đẳng giác của $P, Q$ đối với $\triangle ABC$ là ảnh của nhau qua phép nghịch đảo đường tròn $(O)$.

Tính chất trên được đính kèm trong file dưới đây, mọi người có thể tham khảo .

Quay lại bài toán trên, một điều hiển nhiên là tâm đường tròn $(P_aP_bP_c)$ là liên hợp đẳng giác của $P$ đối với $\triangle ABC$. Gọi $R, S$ thứ tự là liên hợp đẳng giác của $P, Q$ đối với $\triangle ABC$. Thế thì $R, S$ thứ tự là tâm $(P_aP_bP_c)$ và $(Q_aQ_bQ_c)$. Theo tính chất trên thì $R, S$ là ảnh của nhau qua phép nghịch đảo đường tròn $(O)$. Do đó $O, R, S$ thẳng hàng.

Gọi $\triangle R_aR_bR_c$ và $\triangle S_aS_bS_c$ là tam giác pedal ứng với $R, S$ đối với $\triangle ABC$.

Gọi $N_a, N_b, N_c$ là tâm Euler của $\triangle BPC, \triangle CPA, \triangle APB$.

Theo tinh chất 1 và tính chất 3 ở đường link: http://artofproblems..._9point_centers, ta có $\triangle R_aR_bR_c \sim \triangle N_aN_bN_c \sim \triangle S_aS_bS_c$. Do đó nếu gọi $R_{(X)}$ là bán kính đường tròn $(X)$ thì :

$\frac{R_{(P_aP_bP_c)}}{R_{(Q_aQ_bQ_c)}} = \frac{2R_{(R_aR_bR_c)}}{2R_{(S_aS_bS_c)}} = \frac{R_bR_c}{S_bS_c} = \frac{AR}{AS}$. 

Do đó $\frac{OR}{OS} = \frac{AR^2}{AS^2} = \frac{AR^2 - R_{(P_aP_bP_c)}^2}{AS^2 - R_{(Q_aQ_bQ_c)}^2} = \frac{P_{A/(P_aP_bP_c)}}{P_{A/(Q_aQ_bQ_c)}}$. Theo định nghĩa về tỉ số phương tích ta có $(O, OA)$ đồng trục với $(P_aP_bP_c)$ và $(Q_aQ_bQ_c)$. Ta có đpcm $\blacksquare$. 

P/s: bài này nếu không biết nhiều cũng 'khó nhằn" chứ chẳng đùa. 

Mình xin đề nghị bài 33:

Giữ lại các điểm ở Bài đề nghị 1 của baopbc. Chứng minh $(F, FK)$ tiếp xúc $(O)$. 

Chú ý: Mong Bảo chỉ cộng điểm cho ai có lời giải thuần khiết thôi nhé.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 6\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 7\\ \hline QuangDuong12011998 & 3\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

Tranh thủ đêm khuya:
Lời giải:
$BE, CF$ thứ tự cắt lại $(K)$ tại $X, Y$.
Ta có $\widehat{EXF}=\widehat{EDF}=\widehat{BAC}$(do $AEDF$ là hình bình hành) $=\widehat{BNF}$. Do đó $X, B, N, F$ đồng viên. Tương tự thì $Y, C, M, E$ đồng viên.
Đặt $(S)=(CMEY)$, $(R)=(BNFX)$. Theo giả thiết thì ta có: $O, S, P$ thẳng hàng và $O, R, Q$ thẳng hàng.
Ta có $\widehat{ESC}=2\widehat{EMC}=2\widehat{BAC}=\widehat{BOC}$, mặt khác $\triangle ESC, \triangle BOC$ thứ tự cân tại $S, O$ nên $\triangle ESC \sim \triangle BOC$, suy ra $\triangle CSO \sim \triangle CEB$.$(1)$
Ta lại có $\widehat{MSE}=2\widehat{ACM}=\widehat{MPC}$(do $(P;PM)$ tiếp xúc $AC$). Do $\triangle MSE, \triangle MPC$ thứ tự cân tại $S, P$ nên $\triangle MSE \sim \triangle MPC$, do đó $\triangle MSP \sim \triangle MEC$. $(2)$
Sử dụng hai cặp tam giác đồng dạng ở $(1)$ và $(2)$ ta có $\frac{SP}{SO} = \frac{SP}{SM}.\frac{SC}{SO}=\frac{EC}{EM}.\frac{EC}{EB}=\frac{EB}{EA}.\frac{EC}{EB}=\frac{EC}{EA}$. Tương tự thì $\frac{RO}{RQ}=\frac{FA}{FB}$. Mặt khác, $AEDF$ là hình bình hành, nên $\frac{EC}{EA}=\frac{DC}{DB}=\frac{FA}{FB}$. Do đó $\frac{SP}{SO}=\frac{RO}{RQ}$.
Đường thẳng qua $R$ song song $OP$ cắt $PQ$ tại $K$. Theo Thales thì $\frac{SP}{SO}=\frac{RO}{RQ}=\frac{KP}{KQ}$, do đó $KS \parallel OQ$. Dễ thấy $K$ thuộc trung trực $EY, FX$ nên $K$ là tâm ngoại tiếp $\triangle DEF$. Ta có đpcm.
P/s: bài này của thầy hay quá

$\boxed{\text{Lời giải bài toán 37}}$ (Thực sự cảm ơn Bảo nhé )

Ta có $CH'.CA=AH.AC=AD^2=BD^2=BI.BC=CI'.CB$ nên $H', I', G, F$ đồng viên, do đó $\widehat{I'H'C}=\widehat{CGF}$. $DF, DG$ cắt $\gamma$ tại $R, S$. Ta sẽ chứng minh $R, S$ cùng thuộc $H'I'$. 

Chú ý rằng $FH'.FA=FH.FC=FR.FD$ nên $A, H', D, R$ đồng viên, do đó $\widehat{RH'F}=\widehat{FDA}=\widehat{CGF}=\widehat{I'H'C}$, do đó $R, H', I'$ thẳng hàng. Tương tự ta sẽ suy ra $R, H', Q, I', S$ thẳng hàng.

Ta có $\widehat{RSD}=\widehat{RDA}=\widehat{DFG}$, nên $R, S, G, F$  đồng viên. Do đó $MH'.MI'=MF.MG=MR.MS=MP.MC$, do đó $C,P, I', H'$ đồng viên. Gọi đó là đường tròn $\omega$. 

Chú ý rằng $\widehat{H'CQ}=\widehat{SDC}=\widehat{SRC}$ và $\widehat{QCI'}=\widehat{CDR}=\widehat{CSR}$, nên $\triangle CH'Q \sim \triangle RCQ$ và $\triangle CI'Q \sim \triangle SCQ$, do đó $QH'.QR=QC^2=QI'.QS$.

Cuối cùng, xét phép nghịch đảo: $I_{Q}^{QC^2}$ biến $C \leftrightarrow C$, $S \leftrightarrow I'$, $R \leftrightarrow H'$, do đó $(CSR) \leftrightarrow (CH'I')$, mặt khác $\{ C, P \} = (CH'I') \cap (CSR)$ và $C$ là điểm bất động nên $P$ cũng là điểm bất động. Do đó $CQ=QP$ ta có đpcm. 

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 7\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 9\\ \hline QuangDuong12011998 & 4\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

$\boxed{\text{Lời giải bài toán 35}}$

Bổ đề (hiển nhiên):  Cho $\triangle ABC$ và $\triangle DEF$. Khi đó $(AEF), (BFD), (CDE)$ đồng quy $\Leftrightarrow$ $(BCD), (CAE), (ABF)$ đồng quy. 

Áp dụng kết quả: http://www.artofprob...nity/c6h1174125, ta có $(DI_bI_c), (EI_cI_a), (FI_aI_b)$ đồng quy. Theo bổ đề trên ta có: $(I_aEF), (I_bDF), (I_cDE)$ đồng quy tại $T$. Do tính đối xứng nên ta chỉ cần chứng minh $T \in (P^*I_aD)$.

Ta có $\triangle AI_cD \stackrel{+}{\sim} \triangle AP^*I_b$, nên $(I_bP^*, I_bC) \equiv (I_bP^*, I_bA) + (I_bA, I_bC) \equiv (DI_c, DA) + (AI, CI)$ (mod $\pi$). Do đó $(I_cC, I_cD) + (I_bP^*, I_bC) \equiv (CI, I_cD) + (DI_c, DA) + (AI, CI) \equiv (AI, AD)$ (mod $\pi$). 

Ta lại có $\triangle CDI \stackrel{+}{\sim} \triangle CI_cE$ và $\triangle CDP^* \stackrel{+}{\sim} \triangle CFE$ nên $(I_cE, I_cC) + (FC, FE) \equiv (DI, DC) + (DC, DP^*) \equiv (DI, DP^*)$ (mod $\pi$).

Mặt khác, $\triangle CFI_a \stackrel{+}{\sim} CI_bP^*$ và $\triangle AID \stackrel{+}{\sim} \triangle AP^*I_a$ $\Leftrightarrow$ $(I_bP^*, I_bC) \equiv (FI_a, FC)$ (mod $\pi$) và $(P^*I_a, P^*A) \equiv (ID, IA)$ (mod $\pi$).

Kết hợp lại ta có $(P^*I_a, P^*D) \equiv (P^*I_a, P^*A) + (P^*A, P^*D) \equiv (ID, IA) + (P^*A, P^*D) \equiv (AP^*, AI) + (DI, DP^*) \equiv (AI, AD) + (DI, DP^*) \equiv [(I_cC, I_cD) + (I_bP^*, I_bC)] + [(I_cE, I_cC) + (FC, FE)] \equiv [(I_cE, I_cC) + (I_cC, I_cD)] + [(FI_a, FC) + (FC, FE)] \equiv (I_cE, I_cD) + (FI_a, FE) \equiv (TE, TD) + (TI_a, TE) \equiv (TI_a, TD)$ (mod $\pi$). Do đó $T \in (P^*I_aD)$, tương tự ta có đpcm. 

P/S: Bài 21 đã có lời giải ở đây :https://artofproblem...h614826p6455571 của SalaF nên Bảo không cần ghim lại đâu.

Đề nghị $\boxed{\text{Bài toán 38 (AoPS)}}$. Cho $\triangle ABC$ ngoại tiếp $(I)$ và điểm Lemoine $K$. Trung trực $BC$ cắt $IB, IC$ thứ tự tại $A_b, A_c$. Định nghĩa tương tự với $B_a, B_c, C_a, C_b$. Chứng minh $K$ thuộc trục đẳng phương của $(A_bB_cC_a)$ và $(A_cB_aC_b)$.  

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 8\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 9\\ \hline QuangDuong12011998 & 4\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline\end{array}$$

Bài 35/1: Giả sử $c=min(a,b,c)$.
Bất đẳng thức đã cho tương đương:
$\frac{7(a^2+b^2+c^2-ab-bc-ca)}{(a+b+c)(\sqrt{3(a^2+b^2+c^2)}+a+b+c)} \geq \frac{(a-b)^2(a+b)+(a-c)(b-c)(b+c)}{2(a^3+b^3+c^3)}$.
Do $(a-b)^2(a+b)+(a-c)(b-c)(b+c) \leq (a+b+c)(a^2+b^2+c^2-ab-bc-ca)$ nên ta chỉ cần chứng minh:
$14(a^3+b^3+c^3) \geq (a+b+c)^2\sqrt{3(a^2+b^2+c^2)}$.
Sử dụng Cauchy-Schwarz ta có:
$14(a^3+b^3+c^3) \geq 14\frac{(a^2+b^2+c^2)^2}{a+b+c} \geq \frac{14}{9}.\frac{(a+b+c)^3\sqrt{3(a^2+b^2+c^2)}}{a+b+c} \geq (a+b+c)^2\sqrt{3(a^2+b^2+c^2)} \blacksquare$.

Bài toán tổng quát. Cho tam giác $ABC$ và $P$ nằm trong tam giác sao cho $\angle PBA=\angle PCA$. $Q$ là đẳng giác của $P$. $K$ là tâm đường tròn $(QBC)$. $AP$ cắt đường tròn $A$-Apollonius tại $R$ khác $A$. Chứng minh rằng $QR$ và $AK$ cắt nhau trên đường tròn $A$-Apollonius.

 

Figure3881.png

$AK$ cắt $A$-Apollonius tại $L$ khác $A$. Ta sẽ chứng minh rằng $AP, QL$ cắt nhau tại $A$-Apollonius.

$P, Q$ liên hợp đẳng giác trong $\triangle ABC$, kết hợp $\widehat{PBA}=\widehat{PCA}$ ta có $Q$ thuộc trung trực $BC$. Do đó $K$ cũng thuộc trung trực $BC$. 

Gọi đường tròn $A$-Apollonius là đường tròn $(T)$. $AD$ là đường phân giác trong góc $\widehat{BAC}$ của $\triangle ABC$. Hiển nhiên $D \in (T)$.

$AP, AQ$ cắt $(T)$ tại $R, S$. $A, R, S, D$ đồng viên và $AD$ là phân giác $\widehat{RAS}$ nên $DR=DS$. Do đó $R, S$ đối xứng nhau qua $TD \equiv BC$. Cuối cùng ta sẽ chứng minh $QL$ đi qua $R$.

Gọi $M$ là trung điểm $BC$. Ta có: 

$KT^2-KB^2=MT^2-MB^2=(\overline{MT} - \overline{MB})(\overline{MT}+\overline{MB})=(\overline{MT}-\overline{MB})(\overline{MT}-\overline{MC})=\overline{BT}.\overline{CT}=TA^2$.

hay $KQ^2=KT^2-TA^2=P_{K/(T)}=\overline{KL}.\overline{KA}$. Do đó $\widehat{KQL}=\widehat{KAQ}=\widehat{MRL}$. Do $MR \parallel QK$ nên $QL$ đi qua $R$. Ta có đpcm. 

Một lời giải khác cho bài toán tổng quát thứ hai:
$P$ và $Q$ là ảnh nghịch đảo của nhau qua đường tròn $(O)$. Do đó $OA^2=OP.OQ=OK.OR$. Gọi $(J)$ là tâm $(OBC)$ và $O'$ là đối xứng của $O$ qua $BC$. Gọi $M$ là trung điểm $BC$ và $OM$ cắt $(OBC)$ tại $N$. Ta cũng có $OB^2=OM.ON=OJ.OO'$. Do đó $OK.OR=OJ.OO'$ hay $K, R, O', J$ đồng viên. Kết hợp $\triangle OAR \stackrel{+}{\sim} \triangle OKA$, ta có $(RA, RO) \equiv (AO, AK) \equiv (OA, OO') \equiv (OO', O'K)$ (do $O, O'$ và $A, K$ đối xứng nhau qua $BC$) $\equiv (O'J, O'K) \equiv (RJ, RK)$ (mod $\pi$). Do $O, R, K$ thẳng hàng nên $A, R, J$ thẳng hàng hay $AR$ đi qua tâm $(OBC)$ cố định.

$\boxed{\text{Lời giải bài toán 42}}$
$DH$ và $DK$ thứ tự cắt $MB$ và $MC$ tại $P$ và $N$. $DF$ cắt $BM$ và $BI$ tại $R$ và $Z$. $DE$ cắt $CM$ và $CI$ tại $S$ và $Q$. $U$ là hình chiếu của $M$ trên $ID$. $AI$ cắt $BC$ tại $V$.
Ta có $A, M, I$ thẳng hàng nên $B(AMIC)=C(AMIB)$, suy ra $(FRZD)=(ESQD)$. Do đó $EF, RS, ZQ$ đồng quy hoặc đôi một song song. Ta lại có $Z, Q$ thứ tự là trung điểm $DF, DE$ nên $ZQ \parallel EF$. Do đó $RS \parallel EF$. Chú ý $DKEX$ và $DHFY$ là các hình bình hành nên $DP \perp MB$ và $DN \perp MC$. Mặt khác $\frac{\overline{DH}}{\overline{DP}}=\frac{-\overline{FY}}{\overline{DP}}=\frac{-\overline{RF}}{\overline{RD}}=\frac{-\overline{SE}}{\overline{SD}}=\frac{-\overline{EX}}{\overline{DN}}=\frac{\overline{DK}}{\overline{DN}}$. Do đó $HK \parallel NP$. Suy ra $\widehat{DTH}=\widehat{DKH}=\widehat{DNP}=\widehat{DUP}$. Do đó $TH \parallel UP$ và tương tự $TK \parallel UN$. Từ đó ta có $\frac{\overline{DT}}{\overline{DI}}=\frac{\overline{DT}}{\overline{DU}}.\frac{\overline{DU}}{\overline{DI}}=\frac{\overline{DH}}{\overline{DP}}.\frac{\overline{DU}}{\overline{DI}}=\frac{-\overline{RF}}{\overline{RD}}.\frac{\overline{VM}}{\overline{VI}}=\frac{\overline{RF}}{\overline{RD}}:\frac{\overline{ZF}}{\overline{ZD}}.\frac{\overline{VM}}{\overline{VI}}=(FDRZ).\frac{\overline{VM}}{\overline{VI}}=(AVMI).\frac{\overline{VM}}{\overline{VI}}=\frac{\overline{MA}}{\overline{MV}}.\frac{\overline{IV}}{\overline{IA}}.\frac{\overline{VM}}{\overline{VI}}=\frac{\overline{AM}}{\overline{AI}}$. Do đó $MT \parallel AD$. Ta có đpcm.

$$\begin{array}{| l | l |} \hline Ngockhanh99k48 & 9\\ \hline IHateMath & 1\\ \hline fatcat12345 & 5\\ \hline dogsteven & 5\\ \hline baopbc & 10\\ \hline QuangDuong12011998 & 5\\ \hline xuantrandong & 2\\ \hline mrjackass & 1\\ \hline vietnaminmyheart & 3\\ \hline BuiBaAnh & 1\\ \hline halloffame & 2\\ \hline Nguyen Dinh Hoang & 1\\ \hline TQHKTH & 1\\ \hline\end{array}$$

$\boxed{\text{Bài toán 43(AoPS)}}$ Cho tam giác $\triangle ABC$ ngoại tiếp $(I)$. $D, E, F$ là tiếp điểm của $(I)$ với $BC, CA, AB$. $P$ là điểm bất kì. $DP, EP, FP$ thứ tự cắt $(I)$ tại điểm thứ hai $P_a, P_b, P_c$. 

a) Chứng minh $AP_a, BP_b, CP_c$ đồng quy tại $Q$.

b) Gọi $R, S$ là liên hợp đẳng giác của $P, Q$ đối với $\triangle ABC$. Chứng minh $RS$ đi qua điểm cố định. 

$\boxed{\text{Lời giải bài toán 41}}$

Dễ thấy đường tròn $(M; MA)$ đi qua $A, M$ và tiếp xúc $(PBC)$, cắt $CA, AB$ thứ tự tại $E', F'$ là đối xứng của $A$ qua $E$ và $F$. Tương tự đường tròn $(N; NA)$ đi qua $A, Q$ và tiếp xúc $(QBC)$, cắt $CA, AB$ thứ tự tại $G', H'$ là đối xứng của $A$ qua $G$ và $H$. 

Vị tự tâm $A$ tỉ số 2, ta đưa bài toán về chứng minh $E', F', G', H'$ cùng thuộc một đường tròn tiếp xúc $BC$. 

Bổ đề: Cho hai đường tròn $(O_1), (O_2)$ tiếp xúc nhau tại $K$. $X, Y \in (O_1)$ và $Z, T \in (O_2)$ bất kì. Khi đó $(KY, KZ) \equiv (XY, XK) + (TK, TZ)$ (mod $\pi$).

Quay lại bài toán:

$(BPF')$ cắt $BC$ tại điểm thứ hai $X$. Áp dụng định lí Miquel cho $\triangle ABC$ với bộ 3 điểm ${X, E', F'}$ ta có $C, X, P, E'$ đồng viên. 

$(APB)$ cắt $(AQC)$ tại điểm thứ hai $Y$. Ta có $(YP, YC) \equiv (YP, YA) + (YA, YC) \equiv (BP, BA) + (QA, QC) \equiv (BP, BA) + (AQ, AC) + (CA, CQ) \equiv (BP, BA) + (AB, AP) + (CP, CB) \equiv (BP, BA) + (PF', PB)$ (áp dụng bổ đề cho $(BPC)$ và $(M; MA)$ tiếp xúc tại $P$) $\equiv (PF', BA) \equiv (F'P, F'A) \equiv (E'P, E'A) \equiv (E'P, E'C)$ (mod $\pi$). Do đó $C, X, P, Y, E'$ đồng viên. Ta lại có: $(YQ, YB) \equiv (YQ, YA) + (YA, YB) \equiv (CQ, CA) + (PA, PB) \equiv (CQ, CA) + (AP, AB) + (BA, BP) \equiv (CQ, CA) + (AC, AQ) + (BQ, BC) \equiv (CQ, CA) + (QG', QC)$ (áp dụng bổ đề cho $(BQC)$ và $(N; NA)$ tiếp xúc tại $Q$) $\equiv (QG', CA) \equiv (G'Q, G'A) \equiv (H'Q, H'A) \equiv (H'Q, H'B)$ (mod $\pi$). Do đó $B, Q, Y, H'$ đồng viên. Mặt khác $(YP, YQ) \equiv (YP, YA) + (YA, YQ) \equiv (BP, BA) + (CA, CQ) \equiv (BC, BQ) + (PC, BC) \equiv (PC, BQ)$ (mod $\pi$), suy ra $(QY, QB) \equiv (PY, PC) \equiv (XY, XC) \equiv (XY, XB)$ (mod $\pi$) hay $B, X, Q, Y, H'$ đồng viên. 

Chứng minh tương tự như trên ta có $(AQB), (APC), (BPF'), (CQG')$ đồng quy tại điểm $Z$. 

Ở trên ta đã có $(QA, QC) \equiv (PF', PB)$ (mod $\pi$) và $(PA, PB) \equiv (QG', QC)$ (mod $\pi$). Do đó $(E'F', E'G') \equiv (E'F', E'A) \equiv (PF', PA) \equiv (PF', PB) + (PB, PA) \equiv (QA, QC) + (QC, QG') \equiv (QA, QG') \equiv (H'A, H'G') \equiv (H'F', H'G')$ (mod $\pi$). Do đó $E'. F', G', H'$ đồng viên. Hơn nữa $(E'F', E'G') \equiv (PF', PB) + (PB, PA) \equiv (PF', PB) + (QC, QG') \equiv (XF', XB) + (XC, XG') \equiv (XF', XG')$ (mod $\pi$) nên $X \in (E'F'G'H')$. Mặt khác, $(XE', XC) \equiv (PE', PC) \equiv (AC, AP) + (BP, BC)$ (áp dụng bổ đề cho $(M; MA)$ và $(BPC)$ tiếp xúc) $\equiv (F'E', F'P) + (F'P, F'X) \equiv (F'E', F'X)$ (mod $\pi$), do đó $(E'F'G'H')$ tiếp xúc $BC$ tại điểm $X$. Ta hoàn tất chứng minh.

Một tính chất cơ bản của tứ giác toàn phần, đường thẳng Gauss vuông góc với đường thẳng Steiner (đã được đề cập trong tài liệu chuyên Toán Hình học 10). Ta lại có, đường thẳng nối trọng tâm hai tam giác song song với đường thẳng Gauss của tứ giác 

Áp dụng Cauchy-Schwarz ta có
$x(b+c)+y(c+a)+z(a+b) = (a+b+c)(x+y+z)-(ax+by+cz) = \sqrt{[(a^2+b^2+c^2)+2(ab+bc+ca)][(x^2+y^2+z^2)+2(xy+yz+zx)]}-(ax+by+cz) \geq 2\sqrt{(ab+bc+ca)(xy+yz+zx)}+\sqrt{(a^2+b^2+c^2)(x^2+y^2+z^2)}-(ax+by+cz) \geq 2\sqrt{(ab+bc+ca)(xy+yz+zx)}$.

Sử dụng AM-GM ta có:
$a^2+4c^2 \geq 4ac=\frac{8}{b}$. Tiếp tục sử dụng AM-GM ta có: $a^2+2b^2+4c^2-6b \geq \frac{8}{b}+b^2+b^2-6b \geq 3\sqrt[3]{\frac{8}{b}.b^2.b^2}-6b=0$.
Dấu bằng xảy ra $\Leftrightarrow$ $(a,b,c)=(\sqrt{2}, 2, \frac{1}{\sqrt{2}})$

$\boxed{\text{Lời giải bài toán 47}}$

Bổ đề: $(AB, CD) = \omega$ $\Leftrightarrow$ $\frac{1-\omega}{\overline{AB}}=\frac{1}{\overline{AC}}-\frac{\omega}{\overline{AD}}$. (Hệ thức Descartes mở rộng)

Quay lại bài toán:

Tiếp tuyến tại $P$ của $(ABC)$ cắt $AC$ tại $D$. Từ $D$ kẻ tiếp tuyến $DE$ khác $DP$ đến với $(ABC)$. $BE$ cắt $PL$ tại $F$. $BL$ cắt $(ABC)$ tại điểm thứ hai $B'$.

Ta nhận thấy rằng $BAB'C$ và $APCE$ là hai tứ giác điều hòa.

Do đó $P(ACBB')=-1=B(ACPE)$, suy ra $BE, PB', AC$ đồng quy tại $G$.

$BL$ cắt $AC$ tại $B_1$. Bằng đại số ta suy ra $(B'LB_1B)=-2$.

Mặt khác $(PFZX)=B(PFZX)=B(PEAC)=-1$, áp dụng bổ đề ta có: $\frac{2}{\overline{PF}}=\frac{1}{\overline{PZ}}+\frac{1}{\overline{PX}}$.

Ta lại có $(PLYF)=G(PLYF)=G(B'LB_1B)=-2$, áp dụng bổ đề ta có:

$\frac{3}{\overline{PL}}=\frac{1}{\overline{PY}}+\frac{2}{\overline{PF}}=\frac{1}{\overline{PY}}+\frac{1}{\overline{PX}}+\frac{1}{\overline{PZ}}$ $\blacksquare$.

P/s: Thầy (hoặc bạn nào đó) có thể đăng giúp em (mình) bài mới được không ạ?

$\boxed{\text{Lời giải bài toán 48}}$ 

Tương tự y như chứng minh với đường tròn Mixtilinear trong tam giác. Gọi đường tròn $(I)$ nội tiếp tứ giác $ABCD$, đường tròn tiếp xúc $DA, AB$ và tiếp xúc trong $(O)$ gọi là đường tròn $(O_a)$. 

Theo định lí Monge-D'Alembert ta có:

$A$ là tâm vị tự ngoài của $(I)$ và $(O_a)$, $X$ là tâm vị tự ngoài của $(O)$ và $(O_a)$, Do đó $AX$ đi qua tâm vị tự ngoài của $(O)$ và $(I)$. Tương tự ta sẽ có $AX, BY, CZ, DT$ đồng quy tại tâm vị tự ngoài của $(O)$ và $(I)$.

P/s: Thầy (hoặc bạn nào đó) có thể đăng giúp em bài mới được không ạ?

$\boxed{\text{Lời giải bài toán 58}}$

Ta sẽ chứng minh $D$ đối xứng với $L$ qua đường thẳng $EF$. 

Trước hết gọi $L$ đối xứng $D$ qua $EF$ ta sẽ đi chứng minh $AL, OI, BC$ đồng quy. Gọi $K = AL \cap BC$ ta sẽ chứng minh $O, I, K$ thẳng hàng.

$AI$ cắt đường tròn $(O)$ tại điểm thứ hai $N$. Gọi $M, Y, Z$ là hình chiếu của $N$ trên $BC, AB, AC$. $U = AD \cap OM$. $DL$ cắt $OA$ tại $S$. $DI$ cắt $EF$ và $OA$ tại $Z, T$. 

Ta có, theo đường thẳng Simson thì $Y, M, Z$ thẳng hàng. Từ đó qua phép vị tự tâm $A$ ta có $A, Z, M$ thẳng hàng. Dễ thấy $\triangle OAN$ và $\triangle ZLD$ là hai tam giác cân và $\widehat{ONA}=\widehat{ZDL}$ nên $ZL \parallel OA$. Suy ra $\frac{\overline{DZ}}{\overline{DT}}=\frac{\overline{DL}}{\overline{DS}}$. Hay là $\frac{\overline{UM}}{\overline{UO}}=\frac{\overline{DL}}{\overline{DS}}$. Suy ra $D(OKAI)=D(OMUI)=\frac{\overline{UO}}{\overline{UM}}=\frac{\overline{DS}}{\overline{DL}}=A(SLDI)=A(OKDI)$. Từ đó $O, I, K$ thẳng hàng và ta có đpcm.

P/S: Thầy (hoặc bạn nào đó) ra giúp em (mình) bài mới được không ạ?

 

$\boxed{\text{Lời giải bài toán 60'}}$

$AI, BI, CI$ thứ tự cắt $(O)$ tại các điểm thứ hai $A_1, B_1, C_1$. $DP, EP, FP$ thứ tự cắt $(O)$ tại các điểm thứ hai $D_1, E_1, F_1$. Một tính chất quen thuộc của đường tròn Mixtilinear là $AD, BE, CF$ đi qua tâm vị tự ngoài $Q$ của $OI$. 

Áp dụng định Pascal cho 6 điểm đồng viên $\begin{pmatrix} A & E & D_1 \\ B & D &E_1 \end{pmatrix}$ ta có $AE_1$ cắt $BD_1$ tại một điểm $R$ thuộc $PQ$. Do $P, Q$ đều thuộc đường thẳng $OI$ nên ta có $R$ thuộc $OI$.

Lại áp dụng định lí Pascal cho 6 điểm đồng viên $\begin{pmatrix} A & B_1 & D_1 \\  B & A_1 & E_1 \end{pmatrix}$ ta có $A_1D_1$ cắt $B_1E_1$ tại $S$ thuộc $IR$. Do $IR \equiv OI$ nên $S$ thuộc đường thẳng $OI$. Tương tự ta sẽ suy ra được $A_1D_1, B_1E_1, C_1F_1$ đồng quy tại $S$ thuộc $OI$.

Áp dụng định lí Ceva trong đường tròn ta có $\frac{D_1B_1}{D_1C_1}.\frac{E_1C_1}{E_1A_1}.\frac{F_1A_1}{F_1B_1}=1$.

Đường tròn $(O_a)$ tiếp xúc $AB, AC$ thứ tự tại $A_b, A_c$. Đương nhiên ta có $D, A_b, C_1$ và $D, A_c, B_1$ thẳng hàng

Phép vị tự tâm $D$: $V_{D}^{\frac{DO_a}{DO}}: D_1 \rightarrow X, C_1 \rightarrow A_b, B_1 \rightarrow A_c$, kết hợp $XA$ là đường đối trung của $\triangle XA_bA_c$, ta suy ra $\frac{\sin\widehat{XAA_b}}{\sin\widehat{XAA_c}}=\frac{XA_b^2}{XA_c^2}=\frac{D_1C_1^2}{D_1B_1^2}$. Lập các công thức tương tự ta có $AX, BY, CZ$ đồng quy tại $T$.

Một tính chất của $T$: Khi $P$ chạy trên đường thẳng $OI$, liên hợp đẳng giác của $T$ đối với $\triangle ABC$ chạy trên đường ellipse nội tiếp $\triangle ABC$ (inellipse).

 

 

$\boxed{\text{Lời giải bài toán 62}}$

Đường thẳng $IM, DM$ thứ tự cắt $(A; AE)$ tại điểm thứ hai $X, N$. Kẻ tiếp tuyến $Mt$ của $(A; AE)$. Ta có $Mt \parallel BC$. Do đó $\widehat{XNM}=\widehat{XMt}=\widehat{XTD}$, ta suy ra $T, N, D, X$ đồng viên và $\widehat{DNT}=\widehat{DXT}$.
Mặt khác $IM.IX=IE^2=ID^2$. Do đó $\widehat{DXT}=\widehat{IDM}=\widehat{AMN}=\widehat{ANM}$, hay $\widehat{DNT}=\widehat{MNA}$. Do đó $N, A, T$ thẳng hàng.
Gọi $K$ là giao điểm của $(AMN)$ và $(I)$ sao cho $K$ khác phía $A$ với $MN$. $AK$ cắt $DN$ tại $L$. Ta có $AK.AL=AM^2=AE^2$ do $K$ thuộc $(I)$ nên $L$ thuộc $(I)$. Mặt khác $\widehat{KNA}=\widehat{NLA}=\widehat{KLD}=\widehat{KDB}$. Do đó $K \in (NXDT)$. Suy ra $\widehat{KAM}=\widehat{KND}=\widehat{KTD}$, hay $K \in (AHT) \equiv (AT)$. Lại có $\widehat{DKT}=\widehat{DNT}=\frac{\widehat{HAT}}{2}=\frac{\widehat{HKT}}{2}$. Do đó $KD$ là phân giác $\widehat{HKT}$.
Kẻ tiếp tuyến $Kx$ của $(I)$. Bằng cộng góc suy ra $Kx$ cũng là tiếp tuyến của $(AT)$. Do đó ta có đpcm.

$\boxed{\text{Lời giải bài toán 65}}$
Đường thẳng qua $O$ song song $BC$ cắt $AD$ tại $I$. $AD$ cắt $(O)$ tại điểm thứ hai $X$. Khi đó $TD \parallel OX$. $OB, OC$ thứ tự cắt $AD$ tại $Z, Y$. Ta có sẵn $OI$ là phân giác $\widehat{EOF}$. Ta có $\frac{IY}{ID}=\frac{OY}{OC}=\frac{OY}{OX}=\frac{FY}{FD}$. Do đó $FI$ là phân giác $\widehat{DFY}$. Hay $I$ là tâm bàng tiếp đỉnh $O$ của $\triangle OEF$. Từ đó áp dụng bổ đề Sawayama-Thebault ta có đpcm.
P/s: Bảo tiếp tục giúp anh nhé

Đối xứng của $I$ qua đường thẳng $AB$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Biết tọa độ đối xứng của $I$, và $AB$ vè được đường tròn $(ABC)$

Đó chính là bài IMO Shortlist 2009 G6
http://www.artofprob...h355793p1932938

$\boxed{\text{Lời giải bài toán 75}}$.

Ta quy về bài toán sau giải cho dễ nhìn: Cho $\triangle ABC$ trực tâm $I$. $AI, BI, CI$ cắt $BC, CA, AB$ tại $D, E, F$. Gọi $G, H$ thứ tự thuộc $DE, EF$ sao cho $FG \parallel DH$. Chứng minh $AH$ cắt $CG$ tại điểm thuộc đường tròn ngoại tiếp $\triangle ABC$.

Do $FG \parallel DH$ nên $\frac{EF}{EH}=\frac{EG}{ED}$. Kết hợp $\triangle EAF \sim \triangle EDC$, ta có $EA.EC=EF.ED=EH.EG$. Do đó ta cũng có $\triangle EAH \sim EGC$. Suy ra $\widehat{HAB}=\widehat{HAE}-\widehat{BAC}=\widehat{EGC}-\widehat{EDC}=\widehat{GCB}$. Từ đó ta có đpcm.

P/s: Anh Dương có thể post bài tổng quát của anh từ bài đặc biêt hóa được không ạ? Thầy (hoặc bạn nào đó) có thể đề xuất bài mới giúp em (mình) được không ạ?

Bài 76 này hay đấy , bạn lucifer97 có thể post bài tổng quát của bài đặc biệt hóa đó được không?

$\boxed{\text{Lời giải bài toán 76}}$

a) $PO$ và $PE$ lần lượt là phân giác trong và phân giác ngoài của góc $\widehat{APB}$ nên $EF \perp OP$. $EF$ cắt $AB$ tại $X$. $OP$ cắt $AB$ tại $Q$. Ta có $X, I, P, O$ đồng viên nên $\overline{QX}.\overline{QI}=\overline{QP}.\overline{QO}=\overline{QA}.\overline{QB}$ nên theo Maclaurin thì $(QXAB)=-1$. Từ đó ta có ngay $QE, QF$ là hai tiếp tuyến của $(O)$. $EI$ cắt $(O)$ tại điểm thứ hai $F'$. Ta có $EF, EF'$ thứ tự là đối trung và trung tuyến của $\triangle EAB$ nên $FF' \parallel AB$. Do $I$ là trung điểm $AB$ nên $IF = IF'$ và ta cũng có $IF$ và $IE$ đối xứng nhau qua $AB$. Gọi $K$ đối xứng của $F$ qua $AB$ thì $K, E, I, F'$ thẳng hàng và dễ thấy $I$ là trung điểm $KF'$. Ta có $IA^2=-\overline{IA}.\overline{IB}=-\overline{IE}.\overline{IF'}=\overline{IK}.\overline{IE}$. 

Xét phép nghịch đảo đường tròn $(I)$: $I_{(I)}: E \leftrightarrow K, M \leftrightarrow M, N \leftrightarrow N$. Do $E, M, N$ thẳng hàng nên $I, K, M, N$ đồng viên. Hơn nữa do $Q \in AB$ nên $K$ là đối xứng của $F$ qua $AB$ thì $K \in (Q; QE)$.

Mặt khác $P_{I/(Q; QE)}=QI^2-QE^2=QI^2-\overline{QX}.\overline{QI}=\overline{QI}.\overline{XI}=IA^2$ (theo hệ thức Newton). Do đó $(I)$ và $(Q; QE)$ trực giao. 

Qua phép nghịch đảo $I_{(I)}: (Q; QE) \leftrightarrow (Q; QE), MN \leftrightarrow (IMN)$. Do $MN$ tiếp xúc $(Q; QE)$ tại $E$ nên $(IMN)$ tiếp xúc $(Q; QE)$ tại $K$. Do $(O), P$ cố định nên $Q$ cố định. Suy ra $(Q: QE)$ cố định. Tương tự với $(IRS)$. Ta có đpcm.

b) Gọi $O'$ đối xứng của $O$ qua $AB$. $O', I, Q, L, K$ thứ tự là đối xứng của $O, I, Q, E, F$ qua $AB$ nên $I, K, L, Q, O'$ đồng viên. Do đường tròn $(Q; QO)$ đối xứng $(Q; QO)$ qua $AB$ và $(OIEQF)$ tiếp xúc $(Q; QO)$ nên $(IKL)$ tiếp xúc $(Q; QO)$ cố định. Ta có đpcm.

P/s: Thầy (hoặc bạn nào đó) đề xuất giúp em (mình) bài mới được không ạ?

Bạn alo sai rồi , bởi vì $2(a^2+b^2+c^2)+2(ab+bc+ca) \geq 4(ab+bc+ca)$